-
Notifications
You must be signed in to change notification settings - Fork 10
3.3. Fitness Function
This defines a fitness function. The fitness function is provided as one or more factors, each acting on certain genomic nucleotide or amino acid features, which are multiplied to compute the fitness for a single individual.
An empty
<fitnessFunction>
definition corresponds to a neutral fitness function: the fitness of all individuals is the same, regardless of their genome sequence.
Each factor applies to a selection of sites within a single genome feature.
An example of a fitness function block (with two factors):
<fitnessFunction>
<!-- purifying fitness on all amino acids in ABC protein, except for the 4th -->
<purifyingFitness>
<feature>ABC protein</feature>
<sites>1-3,5-7</sites>
<rank>
<order>observed</order>
<breakTies>random</breakTies>
</rank>
<fitness>
<lowFitness>0.5</lowFitness>
<minimumFitness>0.1</minimumFitness>
</fitness>
</purifyingFitness>
<!-- age dependent fitness on alleles corresponding to the entire DE protein -->
<ageDependentFitness>
<feature>DE protein</feature>
<declineRate>0.005</declineRate>
</ageDependentFitness>
</fitnessFunction>
Each factor is applied to a selection of sites in a genome feature. By default, this feature is the genome feature (nucleotides of the entire genome), and the sites are all sites in the feature.
This may be overridden by:
-
<feature>: the name of one of the defined features in the<genome>description. If omitted, genome is assumed. -
<sites>: A comma separated list of single sites or site ranges within the feature. Note that if the feature is an amino acid feature, this refers to amino acid sites, while if the feature is a nucleotide feature, this refers to nucleotide sites.
There are seven pre-defined fitness factors that may be combined to form a fitness function:
| element | description |
|---|---|
<neutralFitness> |
the fitness of all individuals is the same, regardless of their genome sequence. |
<purifyingFitness> |
per-sites fitness is determined from list of ranked states, with some states considered lethal. |
<frequencyDependentFitness> |
fitness is a function of allele abundance |
<ageDependentFitness> |
fitness is a function of allele age |
<exposureDependentFitness> |
fitness is a function of the integral of the abundance over time |
<empiricalFitness> |
per-site fitness determined by static values assigned to each state |
<populationSizeDependentFitness> |
fitness is a function of population size |
This element is included for completeness, although it is not strictly necessary to explicitly identify sites subject to neutral fitness. The Neutral fitness is the default factor applied to any part of a feature that is otherwise not captured by another fitness factor. Under Neutral fitness, all individuals have the same fitness, regardless of their genome sequence.
This fitness function defines the fitness for each state, and acts on each site individually.
All that is needed to define an empirical fitness function is a list of fitness values for each of the possible states (20 for an amino acid feature, 4 for a nucleotide feature). When working with an amino acid feature, a stop codon (TAA, TAG, or TGA) always has a fitness of -infinity.
An example of an empirical fitness function:
<empiricalFitness>
<feature>ABC protein</feature>
<sites>4</sites>
<!-- assign fitness 1 to K, 0.85 to N, and 0.01 to all other amino acids -->
<values>
0.01 <!-- A -->
0.01 <!-- C -->
0.01 <!-- D -->
0.01 <!-- E -->
0.01 <!-- F-->
0.01 <!-- G -->
0.01 <!-- H -->
0.01 <!-- I -->
1 <!-- K -->
0.01 <!-- L -->
0.01 <!-- M -->
0.85 <!-- N -->
0.01 <!-- P -->
0.01 <!-- Q -->
0.01 <!-- R -->
0.01 <!-- S -->
0.01 <!-- T -->
0.01 <!-- V -->
0.01 <!-- W -->
0.01 <!-- Y -->
</values>
</empiricalFitness>
To define an empirical fitness function, you need to define:
-
<values>: A list of fitness values (4 for a nucleotide feature or 20 for an amino acid feature), separated by white-space (space or new-lines), which corresponds to the states in alphabetical order.
A Purifying fitness function assigns fitness values to ordered states according to a piecewise linear model.
For each site, the possible states (4 nucleotides or 20
amino acids) are ordered according to a <rank> definition and each state
is assigned a fitness value according to a <fitness> definition.
Fitness values range between 0
and 1, where '1' corresponds to the most fit state, and '0' to a
lethal state.
<purifyingFitness>
<feature>ABC protein</feature>
<sites>1-3,5-7</sites>
<rank>
<order>chemical</order>
<breakTies>ordered</breakTies>
<probableSet>12</probableSet>
</rank>
<fitness>
<lowFitness>0.5</lowFitness>
<minimumFitness>0.1</minimumFitness>
</fitness>
</purifyingFitness>
Optionally, a <fluctuate> block may define a process which, at
random time points, makes another state the most fit. In this way, the
purifying fitness function may be used to cause a non-stationary
positive selection.
The <rank> block specifies how the possible states at each site
are ordered, from most fit to most deleterious, and defines a set of
probable states.
-
<order>: how the states should be ordered. Possible values are:-
observed: states are ordered by their frequency in the
<sequences>alignment defined in the<genome>description, by decreasing frequency. -
chemical: amino acids are ordered so that the amino acids in the set with chemical properties similar to the most frequent amino acid in the
<sequences>alignment defined in the<genome>description, are ranked before the other states. The sets (in no particular order, and separated by |) are: AVIL|F|CM|G|ST|W|Y|P|DE|NQ|HKR. - hydropathy: idem but using a partition based on hydropathy: IVLFCMAW|GTSYPH|DEKNQR.
- volume: idem but using a partition based on volume: GAS|CDPNT|EVQH|MILKR|FYW
- A custom partition of the states, which is defined by listing them separated by '|' (like the partitions defined above).
- A custom order of probable states, which is defined by listing the probable states from most fit to least fit. (e.g.
QDNTP)
-
observed: states are ordered by their frequency in the
-
<breakTies>: configure whether ties should be broken randomly ('random') or should the state order be used ('ordered') when two states would be given the same rank. -
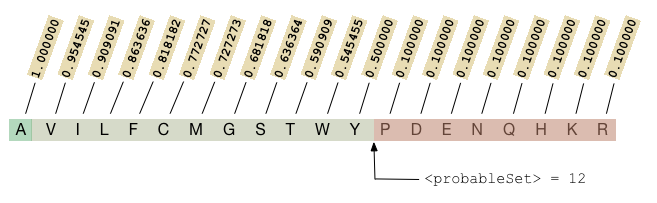
<probableSet>: integer index into the ordered list of possible states or state classes at which the piece-wise linear model defined by<lowFitness>and<minimumFitness>changes value. States prior to the cutoff are assigned linearly decreasing fitness values from1to<lowFitness>; beyond the cutoff states are assigned a fitness value of<minimumFitness>.
Unless the number of probable states are overridden here, it is defined, for each site, based on the order used: when order is observed, only the states with non-zero frequency are probable; when order is based on a partition, only those states in the set with the most frequent state are probable.
Fitness values are assigned to the ranked states, either by specifying
a list of fitness values (with <values>) or based on a piecewise
linear model (with <lowFitness> and <minimumFitness>):
-
<values>: A decreasing list of relative fitness values (4 for a nucleotide feature or 20 for an amino acid feature), all between 0 and 1, separated by white-space (space or new-lines). The most fit should be assigned a value of 1. -
<lowFitness>and<minimumFitness>: Defines a piece wise linear model as in the figure above.
The piecewise linear model has three partitions: the highest ranked state is always assigned a fitness value of 1.
Subsequent states are assigned fitness values that decay linearly from 1 to <lowFitness>.
The number of states in the linear decay region is determined by <probableSet>, which may be set explicitly or will be a assigned a default value.
States ranked below <probableSet> will be assigned a minimum fitness value usually reflecting that those states are completely lethal.
The figure below illustrates assignment of fitness values to the 20 amino acids according to the configuration in the sample block above.
In this example, <probableSet> is used to demarcate low-ranked states which get a minimum fitness value, reflecting low-probability but not lethality.

A purifying fitness function can be transformed into a non-stationary positive selection, by making, at random times, another state the most fit state (i.e. the state with fitness '1'). This process is controlled by two parameters:
-
<rate>: The rate of a Bernouilli process, which is the probability to fluctuate, per site, per generation. -
<fitnessLimit>: Only consider states with at least this fitness to become the new fittest state (default value is 0, allowing any state to become the new fittest state).
This fitness function (as well as the age and exposure dependent fitness functions), considers unique alleles formed by the selected feature sites. Individuals have a same allele if they have exactly the same nucleotide or amino acid sequence at the selected sites.
The frequency dependent fitness function assigns a fitness to an individual based on the frequency of the allele in the population, and assigns a lower fitness to alleles that occur more frequently, using the formula: fitness = 1 - p shape, where p is the frequency (between 0 and 1) of the allele in the population, and shape a parameter that controls how severe more frequent alleles are punished in terms of fitness.
An example of a frequency dependent fitness function:
<frequencyDependentFitness>
<feature>DE protein</feature>
<shape>0.5</shape>
</frequencyDependentFitness>
The fitness function is controlled by a single parameter:
-
<shape>: a positive number affecting the shape of the fitness curve; higher shape values result in curves that penalize frequent alleles more severely: e.g. 0.5 for square root function, 1 for linear, 2 for quadratic, ...

This fitness function (as well as the frequency and exposure dependent fitness functions), considers unique alleles formed by the selected feature sites. Individuals have a same allele if they have exactly the same nucleotide or amino acid sequence at the selected sites.
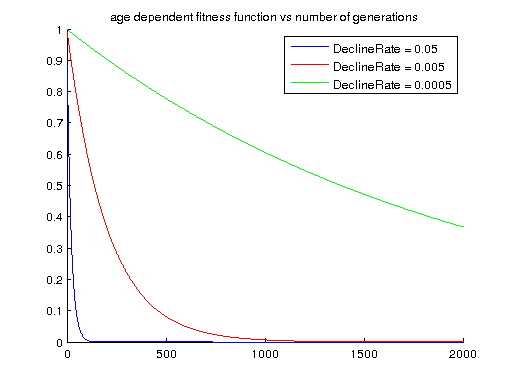
The age dependent fitness function assigns a fitness to an individual based on the age of the allele in the population (since it last appeared), and assigns a lower fitness to alleles that have been continuously present in the population for a longer time, using the formula: f = e -declineRate a, where a is the age (in number of generations) of the allele in the population, and declineRate a parameter that controls how severe older alleles are punished in terms of fitness.
An example of an age dependent fitness function:
<ageDependentFitness>
<feature>DE protein</feature>
<declineRate>0.005</declineRate>
</ageDependentFitness>
The fitness function is controlled by a single parameter:
-
<declineRate>: a positive number indicating how severe older alleles are punished in terms of fitness.
This fitness function (as well as the frequency and age dependent fitness functions), considers unique alleles formed by the selected feature sites. Individuals have a same allele if they have exactly the same nucleotide or amino acid sequence at the selected sites.
The exposure dependent fitness function assigns a fitness to an individual based on how much the allele has been exposed in the population (since it last appeared), and assigns a lower fitness to alleles that have been present for a longer time in a higher prevalence in the population for a longer time, using the formula: f = e -penalty E, where E is the integrated prevalence of the allele over time since its last appearance, and penalty a parameter that controls how severe past exposure is punished in terms of fitness.
In this way, the exposure dependent fitness function is like the age dependent fitness function, but takes into account the prevalence rather then the mere presence of the allele.
An example of an exposure dependent fitness function:
<exposureDependentFitness>
<feature>DE protein</feature>
<penalty>0.01</penalty>
</exposureDependentFitness>
The fitness function is controlled by a single parameter:
-
<penalty>: a positive number indicating how severe more exposed alleles are punished in terms of fitness.
TODO: show figure relating exposure to fitness for different values of the penalty parameter.
Fitness of a region is dependent on population size as a function of a generalized logistic function parameterized by the average fitness in the previous generation, the decline rate, and the maximum population size.

-
<declineRate>: a positive number indicating how previous fitness value is discounted. -
<maxPopulationSize>: a positive integer indicating where the sigmoid function flattens at the top end.
An example of a population size dependent fitness factor.
<populationSizeDependentFitness>
<feature>PR</feature>
<sites>1-30</sites>
<declineRate>0.005</declineRate>
<maxPopulationSize>50000</maxPopulationSize>
</populationSizeDependentFitness>