Grid data structure
The THOR grid is a icosahedral grid, with each face of the icosahedron subdivided in triangles. (for details, see Mendonca, J.M., Grimm, S.L., Grosheintz, L., & Heng, K., ApJ, 829, 115, 2016).
Indices of the icosahedron. Those will be the vertices with pentagon pentagon neighbours (only 5 neighbours instead of 6) and are the primary indices before starting subdivision.
To build a icosahedron, take two poles on top and bottom, the 10 vertices in between lie on two circles on a pentagon, with opposite orientation.
Bottom circle
Top circle
From the initial icosahedron, each face is subdivided in triangles a specified number of times. Between 4 and 7, depending on the subdivision level glevel.
The grid is formed by square tiles, made out of two triangular faces of the icosahedron, for subdivision level 4. For higher subdivision the tiles are subdivided in squares again, so that we always work with tiles of 16x16 vertices.
-
glevel = 4, 4 subdivisions, 1 tile, 2562 points in mesh -
glevel = 5, 5 subdivisions, 2x2 = 4 tiles, 10242 points in mesh -
glevel = 6, 6 subdivisions, 4x4 = 16 tiles, 40962 points in mesh
Grid data is then stored in memory, which needs a linear mapping. The indexing scheme THOR uses is ordered, from slowest changing index to fastest changing index:
- rhomboid face index (0 to 9)
- tile index ky, kx (0 to number of tiles in face side)
- point index in tile j, i (0 to number of point per tile side)
grid layout for glevel = 6. tiles are colored with rainbow colors. Inside tiles, points are colored with increasing saturation along one axis and increasing value along another. We can see that inside one big rhomboïd face of the original icosahedron, all the tiles have the same orientation and it's easy to find indices of neighbour tiles. At interfaces between rhomboïds, the orientation of the indexing axis change between tiles from upper or lower rhomboid and is flipped between edges that go to the same pole (as it's a mapping of a sphere, where sides are folded against each other).
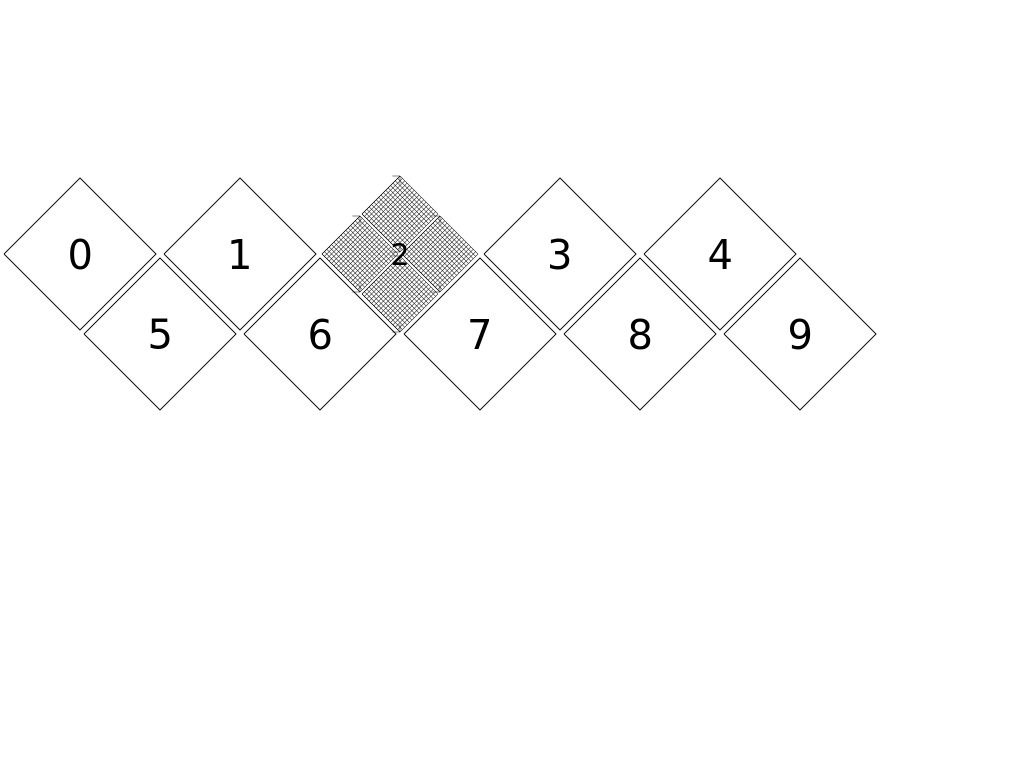The mesh can be unfolded and seen as a tiling of squares.
Each tile is used for computing on small parts of the grid by CUDA kernels. To compute some values, we need access to neighbour points. So a kernel computing on a tile needs to load values from neighbouring tiles. Because of the complex grid layout, the indexing between tiles is not straightforward. Helper functions are provided to load data from neighbouring cells.