Binary Search

Binary Search

If you have a list of numbers and you want to check if a specific number is present in the list, then the most straighforward apporach is using linear search. This means that you compare each element of the list with the element you want to find.

This can be implemented as follows

  int a[7]={9,3,7,2,8,0,1};
  int key = 8;
  int pos = -1
  for(int i=0 ; i<7 ; i++)
  {
    if(a[i] == key)
    {
      pos = i;
      break;
    }
  }

  if(pos != -1) printf("Key %d found at array index %d",key,pos);
  else printf("Key %d is not present in the array\n",key);

Linear search has a worst-case complexity O(N) for an array of size N.

A more efficient algorithm that can be used when the list contains elements in sorted order is Binary Search.

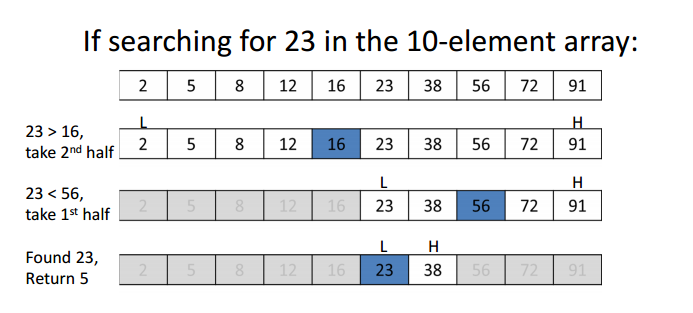
Consider a list A of 10 elements {2,5,8,12,16,23,38,56,72,91} as shown above. Our task is to find 23 in this list.

In binary search, instead of starting from the first element in the list, we consider the middle element. In this case, the middle element is 16. Now, we observe that 16 < 23 and because the list is sorted, all elements to the left of 16 are also <23. This means if 23 is present in the list, it is present to the right of 16.

This way, we can discard half of the elements from our search space. Now, we consider the sub-array from the 6th to 10th element. The middle element this array is 56. Again comparing 56 and 23, we see that 23<56 and so 23 if present in the array will be present to the left of 56. SO we can discard all the elements to the right of 56.

We are left with the subarray {23,38}. Now, the middle element of this subarray is the first element itself. Coomparing this to 23, we see that 23 is present in the list and so we return the position.

Above, we can see that we were able to find a number in a list if 10 element in only 3 iterations. Using linear search this would have taken 6 iterations of a loop.

Binary search has time complexity O(log(N)). You can read the detailed proof here.

The algorithm can be implemented as follows.

Iterative implementation :

int binary_search(int a[] , int n , int key)
{  
  int left,right,mid;
  left = 0 ; right = n-1;

  while(left <= right)
  {
    mid = left + (right-left)/2;

    // If key is found, return the position
    if(a[mid] == key) return mid;

    // if element is less than key, discard the left half of the array
    else if(a[mid] < key) left = mid + 1;

    // Else, discard the right half of the array.
    else right = mid - 1;
  }

  return -1; // This means that element is not present in the array
}

Binary search can also be implemented recursively. You can find this implementation (here There are various other implementations of binary search that can be used in depending on need like finding the lower bound or upper bound for an element, and performing binary search with duplicate elements etc. You can read about these implementations here.