Kratos For Dummies: Stationary heat transfer

Overview

As explained in the home page, the Kratos framework is oriented towards finite element modelling. This is a major advantage when creating standard finite element formulations. In these cases, Kratos will provide most of the tedious code necessary, such as assembling the matrices, solving the system, printing the results in a file, and other task that would probably be more time consuming than transcribing the formulation itself into programming code. The aim of this tutorial is to describe step by step the implementation of a really simple element using as much as possible all these tools provided by Kratos. This way, we'll only have to create the element, boundary conditions and then tell Kratos that our problemtype is a standard FEM. At first the code might seem a little scary but we'll try to explain the lines as much as possible. Let's begin!

(it must be noted that the framework is completely flexible and we could create a problemtype without even creating an element that does something, for example in edge based formulations)

Contents

1. Basic description of the problem and main tools of Kratos used:
   1. Components:
   2. Residual-based builder and solver:
2. Structure of the problemtype and other components:
   1. Basic Structure of Conditions and Elements:
   2. Python Scripts:
   3. Files needed in our application:
3. Sections of this tutorial:
   1. Creating our application: PureDiffussion:
   2. Editing the main files of the application and creating elements and conditions:
   3. Creating a first problem to be solved:
      1. Launching and viewing the postprocess file:
      2. Using the GiD problemtype:

Basic description of the problem and main tools of Kratos used:

We'll create the simplest possible finite element formulation. For that purpose we'll create an application that solves a stationary heat conduction problem for 2D. This is a diffusion only problem with only one degree of freedom (DoF) per node.

In this problem we're going to use a residualbased formulation. Kratos already has a solver so we won't have to program it.

As seen in the previous section, our problem consists of a simple rigidity matrix K , that depends only on the geometry and the scalar permittivity (a closer look reveals that is simply the Laplacian matrix multiplied by this scalar). The other components of our problem are boundary conditions, which we'll assume fixed or free, and thermal loads.

Components

The rigidity matrix will be calculated element by element, adding the rigidity of each element K to the global matrix. This reveals the first tool needed in our problemtype: an element.

For the Dirichlet conditions, since we're using a residual-based calculation we'll have to multiply our boundary conditions by the K matrix. This can be done both element-wise once we have K or at the end of the problem. We chose to do it element-wise.

Finally, for the nodal thermal loads we have to add them node by node and add it to the right hand side vector of the system of equations (RHS). To do so we'll use a tool in Kratos called Condition.

As you can see, we now have our main application components:

• An element (loop in elements, including K and Dirichlet conditions)
• A condition (loop in nodes)

Residualbased builder and solver

What is missing is a tool to assemble all these components. We could do it "by hand", but it is much simpler if we just use a builder and solver. Kratos include a residual-based builder and solver. This way we only have to declare in our problem-type that we'll be using this tool and which are the elements and conditions. And that's it. We won't even need to tell the builder to loop the nodes or elements, just declaring them and then initializing the solver is enough and the process will be done.

Of course, to do so we'll have to respect the structure for both the element and conditions, but this is achieved by simply copying an existing one and modifying it to suit our needs, as will be seen below.

Structure of the problemtype and other components

Basic Structure of Conditions and Elements

Elements and Conditions are both classes in C++ that include a series of subroutines required by the builder and solver. They both share the following structure. An element or condition should contain at least this public methods, in pseudo code:

class mycondition
           void CalculateLocalSystem
           void CalculateRightHandSide
           void EquationIdVector
           void GetDofList

Python Scripts

At his point we have explained the code needed inside Kratos to solve a Poisson problem. However no information regarding loading the model or telling Kratos that we want to execute our problemtype was given. All these tasks are not compiled in the Kratos, they're simply executed by python scripts. Some of them will belong to our problemtype itself and other will be contained inside the folder of the specific problem to be solved.

The big advantage of using these scripts over compiled code is that changes can be done really quicky, for example changing the tolerance of a solver or even changing boundary conditions. Of course, since it's interpreted languange it will be slower; so it's better to limit its use to simple, non iterative tasks as much as possible.

In this sense, the python scripts do the following tasks:

• Load Kratos and import our application
• Read the problem data and create the model part in Kratos: Mesh, elements, materials, variables, degrees of freedom
• Define the Builder&Solver used
• Call the solver
• Write a file with the mesh and results

Files needed in our application

• PureDiffusionApplication/
  • custom_elements/
    • poisson.h
    • poisson.cpp
  • custom_conditions/
    • point_source.h
    • point_source.cpp
  • custom_python/
    • pure_diffusion_python_application.cpp
  • python_scripts/
    • static_poisson_solver.py
  • pure_diffusion_application.h
  • pure_diffusion_application.cpp
  • pure_diffusion_application_variables.h
  • pure_diffusion_application_variables.cpp
  • PureDiffusionApplication.py
  • CMakeLists.txt

The application wil be executed to solve an specific problem defined in few files oustide Kratos:

• SpecificProblem/
  • MainKratos.py
  • my_problem.mdpa
  • ProjectParameters.json

Now you should have an idea of the components we'll need in our code. So hands at work with C++ and Python.

Sections of this tutorial

Creating our application: PureDiffussion

To begin with we must create a new application. Using cmake this is a straightforward task. Since we have a pure diffusion problem we'll name it PureDiffusion. To do so follow the steps in the How to Create Applications tutorial. Therefore we'll navigate to the application_generator folder and call the python script with our application custom name:

cd path/to/Kratos/kratos/python_scripts/application_generator
python laplacian_application_example.py PureDiffusion

Once you've followed all the steps and compilled the application you should be able to import your newly created application, although it is not able to do anything for the moment.

Editing the main files of the application and creating elements and conditions

1. Tutorial:Editing the main files
2. Tutorial:Creating the Element
3. Tutorial:Creating the Conditions
4. Modify the pure_diffusion_python_application.cpp file in the folder custom_python so that we can add our new variable from python (the others are included in the Kernel so we only need to add POINT_HEAT_SOURCE:

// Registering variables in python 
KRATOS_REGISTER_IN_PYTHON_VARIABLE(POINT_HEAT_SOURCE)

5. Tutorial:Creating an Utility (optional): Once you've completed these 4/5 first steps and compiled the kratos you have all the c++ code necessary for your application. So compile the Kratos and the rest of the tasks can be managed using python, which has the advantages mentioned above. So now we proceed with the python scripts required.
6. Tutorial:Creating the Python Solver file: After you've finished these 6 steps your new application is ready. what is left is creating the particular files of our problem.

Creating a first problem to be solved

Despite the GiD interface can both create and launch the files needed to solve a problem, we'll start by writing 'by hand' a very simple example so that we understand the instruction we're giving KRATOS through the python interface we have just created in the previous step. Actually when you launch an example from the GiD interface of Kratos, this is what is going on behind: First GiD creates a geometry file that Kratos can understand, the .mdpa , and then it executes a python scripts that contains all the instruction for kratos. Like read the geometry, add degrees of freedom, solve the system, print the results...

So hands at work! We need these two files to launch an example:

• A .mdpa (meaning modelpart) file defining the geometry, material, loads, etc.
• A .py file to tell KRATOS what to do with that file.

For our first problem we'll create a simple, two element problem:

with CONDUCTIVY=10.0, we'll fix the TEMPERATURE=100.0 in node 1 and we'll add a POINT_HEAT_SOURCE=5.0 in node 3

with this information, the model part file looks like this:

example.mdpa

Begin ModelPartData
//  nothing here
End ModelPartData


Begin Properties 1            
CONDUCTIVITY 10.0 // all the elements of the group 1 (second column in the list of elements) will have this property
End Properties

Begin Nodes
       1        0.0        0.0         0.0                               //node number, coord x, cord y, coord z
       2        1.0        0.0         0.0                               //node number, coord x, cord y, coord z
       3        1.0        1.0         0.0                               //node number, coord x, cord y, coord z
       4        0.0        1.0         0.0                               //node number, coord x, cord y, coord z
End Nodes

Begin Elements Poisson2D //here we must write the name of the element that we created
  1 1 1 2 4   //pos1:elem ID ; pos2:elem Property ( = 1 in this case) ; pos3 - pos5: node1-node3    
  2 1 3 4 2   //pos1 and pos2 are always id and property. if the elem had 4 nodes, we woud add a 6th column for the last node    
End Elements

Begin NodalData TEMPERATURE          //be careful, variables are case sensitive!
1 1 100.0                // pos1 is the node, pos2 (a 1) means that the DOF is fixed, then (position 3) we write the fixed displacement (in this case, temperature)  
End NodalData

Begin NodalData POINT_HEAT_SOURCE             
3    0    5.0             //fixing it or not does not change anything since it is not a degree of freedom, it's just info that will be used by the condition  
End NodalData

Begin Conditions PointSource
1 1 3     //pos1:condition ID(irrelevant) ; pos2:cond Property ( = 1 in this case) ; pos3:node to apply the condition. if it was a line condition, then we would have 4 numbers instead of 3, just like elements              
End Conditions

and our python file:

example.py

##################################################################
##################################################################
#setting the domain size for the problem to be solved
domain_size = 2  # 2D problem  

#including kratos path
import sys
from KratosMultiphysics import *    #we import the KRATOS  
from KratosMultiphysics.PureDiffusionApplication import *        #and now our application. note that we can import as many as we need to solve our specific problem 

#defining a model part
model_part = ModelPart("ExampleModelPart");  #we create a model part  

import pure_diffusion_solver           #we import the python file that includes the commands that we need  
pure_diffusion_solver.AddVariables(model_part)  #from the static_poisson_solver.py we call the function Addvariables so that the model part we have just created has the needed variables 

 # (note that our model part does not have nodes or elements yet) 

 #now we proceed to use the GID interface (both to import the infomation inside the .mdpa file and later print the results in a file  
gid_mode = GiDPostMode.GiD_PostAscii  #we import the python file that includes the commands that we need  
multifile = MultiFileFlag.SingleFile
deformed_mesh_flag = WriteDeformedMeshFlag.WriteUndeformed
write_conditions = WriteConditionsFlag.WriteElementsOnly
gid_io = GidIO("art4",gid_mode,multifile,deformed_mesh_flag,write_conditions)

model_part_io = ModelPartIO("example")             # we set the name of the .mdpa file  
model_part_io.ReadModelPart(model_part)         # we load the info from the .mdpa 

 # we create a mesh for the postprocess  
mesh_name = 0.0
gid_io.InitializeMesh( mesh_name );
gid_io.WriteMesh((model_part).GetMesh());
gid_io.FinalizeMesh()

#the buffer size should be set up here after the mesh is read for the first time  (this is important for transcient problems, in this static problem =1 is enough)  
model_part.SetBufferSize(1)

 # we add the DoFs  
pure_diffusion_solver.AddDofs(model_part)
   
#creating a solver object
solver = pure_diffusion_solver.StaticPoissonSolver(model_part,domain_size)
solver.time_order = 1
solver.echo_level = 0
solver.Initialize()


print ("about to solve!")    
solver.Solve()
print ("Solved!")  


#and we print the results  
gid_io.InitializeResults(mesh_name,(model_part).GetMesh()) 
gid_io.WriteNodalResults(TEMPERATURE,model_part.Nodes,0,0)
gid_io.FinalizeResults()

#since we have already calculated the temp, we can get the mean value
#first the constructor (it could have been called before)
calc_mean=CalculateMeanTemperature(model_part)
#and we calculate!
calc_mean.Execute()

Launching and viewing the postprocess file

Once you have both files, you must open a console, go the directory where you created both files and type:

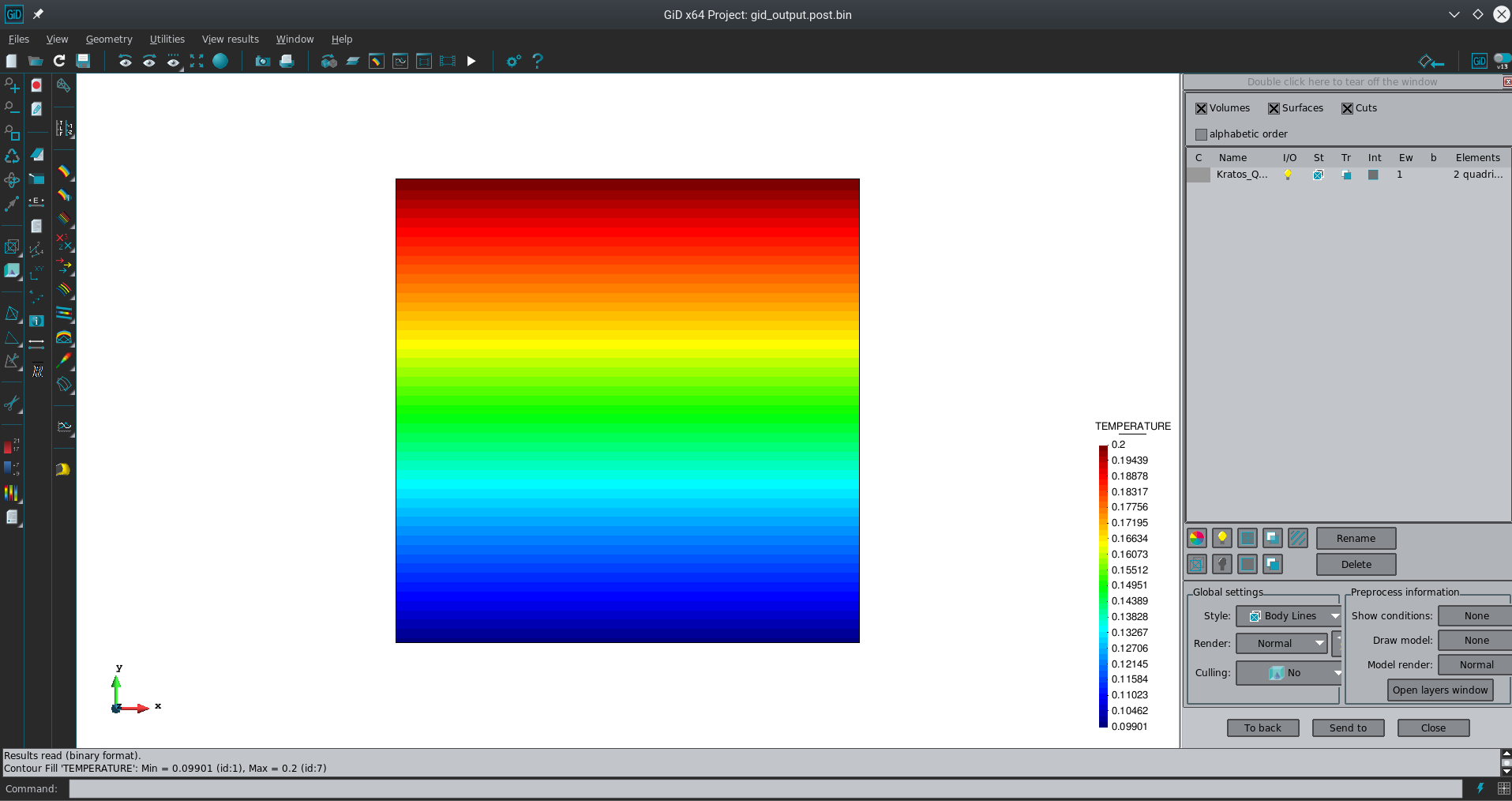
python example.py

This launches the script you've created and several files are created after it has finished. The ones we are interested in are output.res and output.msh (results and mesh respectively). They are ASCII files so you can view them using the text editor you prefer. Alternatively, you can open the .res with GiD to visualize them. The result should look like this:

Congratulations!, you have successfully created and launched your first python application.

Using the GiD problemtype

NOTE: There is a new interface in GiD, the interface example is not implemented yet.

Using the GiD interface allows you to manage much more complex geometries. Moreover, you can launch Kratos directly from the (visual) GiD interface, so there's no longer need to use a console. To do so simply download File:PureDiffusion.gid.zip and unzip it inside the GiD problemtypes folder. The interface is really easy to use so you should have no problems understanding how to use it.