-
Notifications
You must be signed in to change notification settings - Fork 23
QuantoDerive
QuantoDerive is the new scala-based GUI that will replace the existing Quantomatic GUI. These pages are for planning various aspects of the tool. QuantoDerive uses a theory-based idiom for defining systems of axioms and using axioms to perform derivations. Fundamentally, it is an interactive theorem prover which uses a fixed bag of methods for constructing proofs.
There are a few basic concepts that are central to QuantoDerive.
- Theory - a signature, along with a collection of axioms, theorems, and proofs
- Signature - details about how the generators of a particular theory are visualised and implemented in the core
- Axioms - rules that do not need to be proven. Possible aliases: "postulate", "definition".
- Theorems - a rule, plus one or more goals. The rule is considered "valid" (i.e. sound, usable in other proofs) if each of its goals has a valid derivation.
- Goals - rules that need to derived to establish the truth of a theorem. These can also introduce new local rules (assumptions), e.g. induction-hypothesis
- Derivations - sequences of rewrite steps. A derivation validates (aka proves) a goal if each of its steps is valid and it starts with the LHS of the goal and ends with the RHS of the goal.
A QuantoDerive project is a directory (or zip file) with the *.qtheory extension, consisting of various JSON files:
-
main.qsig- the main signature -
*.qaxiom- axioms and definitions -
*.qgraph- "scratch" graphs. These can be edited and used as a starting point for derivations. -
*.qtheorem- theorems, lemmas, corollaries. These files store a theorem name, proof type, and derivations for each of its goals.
For more info on graph, rule, and theory formats, see file formats.
Following the project/IDE style, the (directory or logical) structure of the project is displayed on the side, with a main editing area in the centre. Theories can be modified using three distinct modes of editing, which are activated depending on what kind of file is in focus. The three modes of editing are as follows.
- Graph Editor - for auxiliary and scratch graphs
- Axiom/theorem Editor - for axioms and theorems
- Derivation Editor - for derivations
A central concept in QuantoDerive is that of validation. For a theorem to be valid, it must be connected to a valid derivation. For a derivation to be valid, every step must be an axiom or another valid theorem. Thus, the validity of one theorem can depend on the validity of another. Clearly this dependency relation must be well-founded, with the bottom elements all axioms. More details are given below.
To give an idea of what theorems look like, here are some examples. The simple type establishes a theorem by a single derivation (with no local assumptions).
-
Theorem:
hopf -
Provides:
G = H -
By:
simple -
Goals:
-
Main:
[] ==> G = H
-
Main:
The induction type corresponds to proof by !-box induction.
-
Theorem:
spider_merge -
Provides:
G = H -
By:
induction(b) -
Goals:
-
Base:
[] ==> kill_b_G = kill_b_H -
Step:
[assms.IH := (fix_b_G = fix_b_H)] ==> expand_b_G = expand_b_H
-
Base:
In the core, theorem types correspond to rule tactics. Though at some point, we might make these honest tactics and define an LCF-style kernel based on rewriting, in the mean time, these are just ML functions. They take in a rule, some (optional) string/name arguments, and produce a list of goals (or NONE if the tactic doesn't apply).
rule_tac : rule -> string list -> (goal list) option
goal := { name: string, assms: (string * rule) list, shows: rule }
Examples are simple, which is basically the identity tactic, induction which does !-box inductions, and additional inference rules for !-boxes, e.g. merge. In the case where proofs are very simple, these could be done inline. For example, it may get unweildy if a whole new theorem was required to do single !-box operations on existing rules.
The graph editor can be run stand-alone or (ultimately) inside of QuantoDerive. Its designed to be as simple as possible, and does not need to communicate with the core. It loads and saves files in the .qgraph file format.
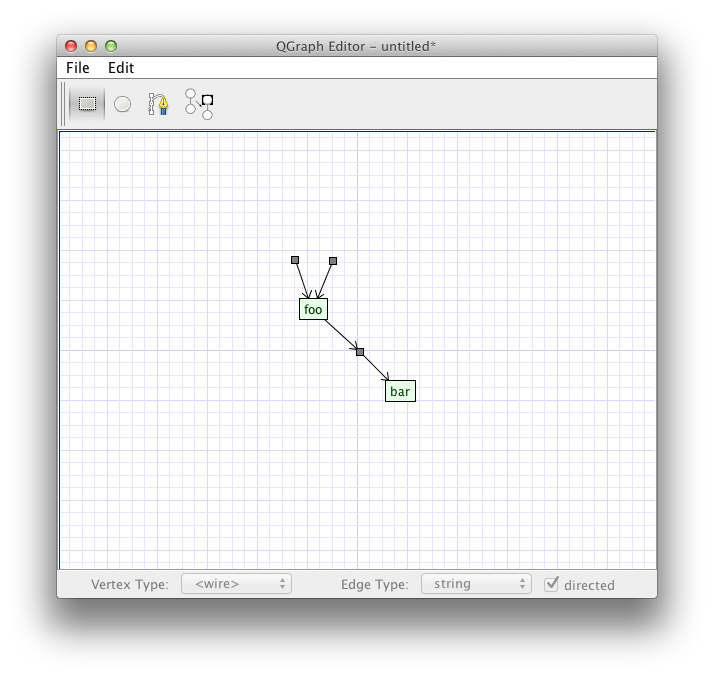
Many aspects of the interface are obvious, so here are suggestions on how to do the less obvious things.
The graph editor should not force the user to work with wire-vertices directly. Instead, they should be working with the derived notion: wires. Thus (non-boundary) wire-vertices are supressed in the display of the graph. Wires are added using a special wire adding tool, rather than by adding some wire-vertices and connecting them up by edges.
The Add Wires tool works a bit like the old add edge tool, but with a few important differences. Firstly, how the tool behaves depends largely on whether the mouse down happens in open space, on a boundary, or on a node-vertex. I'll break these into cases. First, here are the cases where the mouse-down happens in open space:
- Open space => Open space (same point) : create a circle
- Open space => Open space (different point) : create a bare wire
- Open space => Node-vertex : create an input wire
- Anything else starting with Open space : no-op
Next, boundaries:
- Boundary => Open space : no-op
- Boundary (output) => Node-vertex : attach this wire to the node-vertex
- Boundary (output) => Boundary (input) : plug wires together
- Anything else starting with Boundary: no-op
Finally, node-vertices:
- Node-vertex => Boundary (input) : attach this wire to the node-vertex
- Node-vertex => Open space : create an output wire
- Node-vertex => Node-vertex : create an internal wire
For drags starting at node-vertices or open space, the user will see the normal red line with two endpoints indicating where the wire will go. For drags starting on boundaries, there are two options for how things should look to the user mid-drag.
The first is that we treat boundaries just like the other two cases and display a red line indicating what (if any) pluggins will be made. If the user tries to drop the other end on an invalid place (e.g. tries to connect to an output) the red line simply disappears. This has the advantage that, in the event of a no-op, nothing about the graph's appearance seems to change. This has the disadvantage that the red line has a clear direction, so its not obvious whether dragging from an input (or worse, a node-vertex) to an output should produce a plugging or a no-op.
The other option is that a boundary actually moves when the user drags it. If the user drops it on a compatible location, the plugging is made. If not, the boundary returns to its original location. In this case, it probably makes sense to allow the user to drag inputs on to outputs and node vertices as well as vice-versa. The down sides are (1) that boundaries have to be treated specially, and (2) its not clear what happens if the user drops a boundary in open space. It would feel odd if this were treated as a no-op. It is no real problem to just move the boundary, but then it is redudant (in that the move tool does the same thing).
!-boxes are add via the Add !-Box tool. With this tool selected, the user can drag boxes around collections of vertices to ! them. They can also be modified when the Select tool is active (TODO: decide whether to let !-box editing be its own tool). !-boxes can be edited in various ways. Most of these have to do with working with the "hot corner" of the !-box, which can be thought of as logical !-node which connects to the contents of the box. (See arXiv:1204.6695 for how this works).

Delete a !-box by selecting it and pressing the DELETE key. Add child vertices or !-boxes by dragging a line from the corner of the !-box to the vertex or child !-box. When a !-box is selected, it will show lines connecting the corner of the !-box to any of its child vertices or !-boxes. Centred on each of these lines is a small X the user can click to remove the child from the !-box. The lines and the X'es should be light and unobtrusive (perhaps becoming darker on mouse-over) to not confuse the eye.
Rules are edited much as before, in a side-by-side manner. One notable difference is that boundaries are visually (and semantically) distinguished from other wire vertices. Boundaries are created by a distinct tool, not available in the graph editor, which creates a boundary in the same physical position on both sides of the rule. The boundary vertices on the LHS and the RHS are then locked to each other, so when the user moves or deletes the boundary on one side, the change occurs simultaneously on the other side.
!-boxes are treated in a similar manner. When they are created/deleted/nested/un-nested, this operation happens jointly. Also, when a boundary vertex is added or removed from a !-box, this happens jointly.
When the user tries to save, the client checks that all other (non-boundary) wire vertices have exactly one input and one output. Otherwise, it will refuse to save.
At any point while editing a graph, the user can click a button to start a derivation. This creates a new derivation starting at the open graph and opens the derivation editor. While performing a derivation, the user constructs a proof history, which is essentially a tree whose nodes are labelled by applications of rewrite rules. It will look something like this:

Unlike the usual notion of a proof, where the history is linear, a derivation is more free-form in that it allows branching. This affords two benefits. Firstly, it allows experimentation while searching for a proof, and secondly, it can succinctly express multiple proofs that start the same way.
A derivation tree has two kinds of nodes: proof steps (shown in black above) which represent a rule that has already been applied, and proof heads (shown in white), which mark a position from which a proof can be continued. What the user sees in the main area depends on what kind of node is selected.

If a proof head is selected, then the current graph is displayed on the left, and available rewrites are displayed on the right. By default, as soon as the user clicks on a head, it starts searching for rewrites in the entire graph. This is done asynchronously so the user doesn't lose responsiveness while this happens. To narrow down the rewrites, the user can select a subgraph and hit spacebar to filter rewrites to only those matching the selected graph. Various other commands for working with subsets of rewrites, etc. are also supported.
A proof step displays the graph prior to rewriting on the left, and the graph after rewriting on the right. On the left, it highlights the section of graph that was removed, and on the right, the section that was added. The user can perform various commands from here.
If this proof step is the last step before the proof head, the user may delete the proof step and roll back to its parent. The user may also create a new branch. In this case, a new proof head is added as a child of the current proof step and the history advances there. If the user navigates away from this proof head without performing a proof step, the proof head is removed.
It also has several buttons for navigating the derivation. Back and forward behave has expected, except in the case where a proof step has multiple successors. In this case, it could either (a) ghost, forcing the user to manually select a successor from the history or (b) prompt the user for which branch to take.
Another alternative would be to show all of the successors on the RHS, each with their own "next" button.
When a project is loaded or changed, theorems may need to be re-checked. A theorem is said to be valid if the derivation of each of its goals is valid. A valid derivation is a derivation where each of its steps is a well-formed rewrite rule (i.e. shared boundary and !-boxes) that is unifiable against an axiom or another valid theorem. Theoretically, a rule L <- B -> R validates another rule G <- C -> H if there exists a double-pushout diagram where L <- B -> R defines the top edge and G <- C' -> H the bottom edge, for some C'.

We can define a dependency relation for theorems and axioms. A theorem depends on a theorem or an axiom if it occurs as a step in one of its derivations. Note that theorems do not need to be stated or proved in any particular order, provided the dependency relation between theorems doesn't have any cycles, and all the bottom elements are axioms.
Before talking about validating theorems, we define the procedure for validating one rule against another.
A rewrite rule R1 is said to validate R2 if R1 can be used to rewrite lhs(R2) to a new graph H such that there is a boundary-preserving isomorphism between H and rhs(R2). In other words, up to some renaming, R1 can be applied to lhs(R2) to get rhs(R2). In the case where R1 validates R2, the soundness of R1 implies the soundness of R2.
Except in certain corner cases where matching is undecidable (wild !-boxes), the validation problem is always decidable. Naively, this can be done by enumerating all of the possible matchings of R1 on to lhs(R2), rewriting, and performing a graph isomorphism check. In the worst case, rule validation is O(2^(2n)). Fortunately, most validations can be trivialised with some heuristics and a bit of caching.