UNIVERSIDAD PERUANA DE CIENCIAS APLICADAS

TRABAJO FINAL

Curso: Complejidad Algorítmica

Sección: WS6B

Docente: Canaval Sánchez, Luis Martín

Integrantes:

Méndez López, Sebastián Alonso – U202211561

Centurión Quintana, Henry Manuel – U20221A339

Rolando Mochcco, Yordy - U201923959

Tabla de Contenido

1. Descripción del problema
   1.1. Descripción
   1.2. Fundamentación del problema
   1.2.1. Algoritmo de Backtracking
   1.2.2. Algoritmo de divide y vencerás
   
2. Descripción y visualización de espacio de búsqueda
   2.1. Espacio de búsqueda
   2.2. Estado inicial
   2.3. Estado final
   2.4. Transiciones
   2.5. Representación
   2.6. Representación mediante grafos
   2.7. Cálculos de tamaño
   2.8. Visualización
   2.8.1. Gráfico de una porción representativa del espacio de búsqueda
   
3. Propuesta
   
4. Diseño de la aplicación
   4.1. Análisis de requisitos
   4.2. Especificación
   4.3. Diseño y arquitectura
   4.4. Programación
   4.5. Análisis de complejidad
   
5. Validación de resultados y pruebas
   5.1. Análisis de los resultados
   
6. Conclusiones
   
7. Bibliografía
   

1. Descripción del problema

En el presente documento se hablará sobre la descripción y fundamentación del problema citando fuentes.

1.1. Descripción

En el ámbito de la programación, se encuentran diversas herramientas y enfoques destinados a abordar problemas específicos, pero no todos resultan igualmente efectivos. El problema que nos compete en este proyecto radica en la creación de un sistema interactivo capaz de generar y resolver Sudokus de tamaño n x n. Un Sudoku es un acertijo lógico y numérico donde el objetivo es rellenar una cuadrícula de dimensión n x n de tal manera que cada fila, cada columna y cada subcuadrícula de tamaño n x n contenga todos los números del 1 al n exactamente una vez. El Sudoku es un problema ampliamente reconocido en el campo de la informática y la teoría de la complejidad. Según Johan Ekström y Kristofer Pitkäjärvi (2014), se ha demostrado que resolver un Sudoku es NP-completo (Nondeterministic Polynomial time), lo que impone limitaciones sustanciales a la capacidad de resolver Sudokus a medida que aumenta la complejidad. Aunque los Sudokus de órdenes bajos (3x3, 4x4) generalmente no presentan un desafío computacional en la actualidad, lograr implementaciones eficientes para resolverlos puede servir como demostración de concepto para otros algoritmos similares diseñados para resolver problemas NP-completos. En este sentido, hallar algoritmos eficientes para la resolución de Sudokus puede sentar precedentes para el desarrollo de otros algoritmos.

1.2. Fundamentación del problema

Aplicación en la Vida Real: Los Sudokus son una forma popular de entretenimiento y desafío lógico que se encuentra en periódicos, revistas y aplicaciones móviles. Además de su popularidad en el ámbito recreativo, se utilizan en la enseñanza de la lógica y la resolución de problemas. La generación y resolución de Sudokus son procesos relevantes en la creación de contenidos para estos propósitos.

Representación como Grafo: Un Sudoku se puede representar como un grafo, donde cada celda es un nodo y las restricciones de fila, columna y sub cuadrícula se traducen en arcos entre los nodos. Esto permite la aplicación de algoritmos de búsqueda y técnicas de resolución de grafos para encontrar soluciones válidas.

Búsqueda y Resolución: Resolver Sudokus es un problema NP-completo, lo que significa que encontrar una solución puede ser costoso computacionalmente. Esto brinda una oportunidad para explorar diversas técnicas de búsqueda, como búsqueda en profundidad, búsqueda en anchura, búsqueda heurística y búsqueda en ramificación y poda. Los algoritmos de resolución deben ser eficientes para manejar Sudokus de tamaños variables.

En conclusión, para resolver el problema necesitamos entender el algoritmo backtracking y el algoritmo de divide y vencerás.

1.2.1. Algoritmo de backtracking

El algoritmo de backtracking es utilizado para encontrar soluciones a problemas combinatorios, en los que se busca una combinación de elementos que cumpla ciertas restricciones. Es especialmente útil para problemas donde se necesita explorar diferentes posibilidades en un árbol de decisiones y encontrar la combinación óptima o una solución válida. El algoritmo de backtracking funciona a través de pasos recursivos en los que se toman decisiones en cada etapa, se exploran las posibles soluciones y se revierten esas decisiones si no llevan a una solución válida. Si se encuentra una solución válida, se devuelve; si no, se retrocede (de ahí el nombre) y se prueban otras opciones. Este tipo de algoritmo se utiliza en una variedad de problemas, como la resolución de laberintos, la generación de combinaciones o permutaciones, el Sudoku, la coloración de grafos, entre otros. Es especialmente valioso para problemas que implican una búsqueda exhaustiva en un espacio de soluciones, donde se necesita explorar múltiples combinaciones posibles de manera eficiente y encontrar la solución óptima o válida.

1.2.2. Algoritmo de divide y vencerás

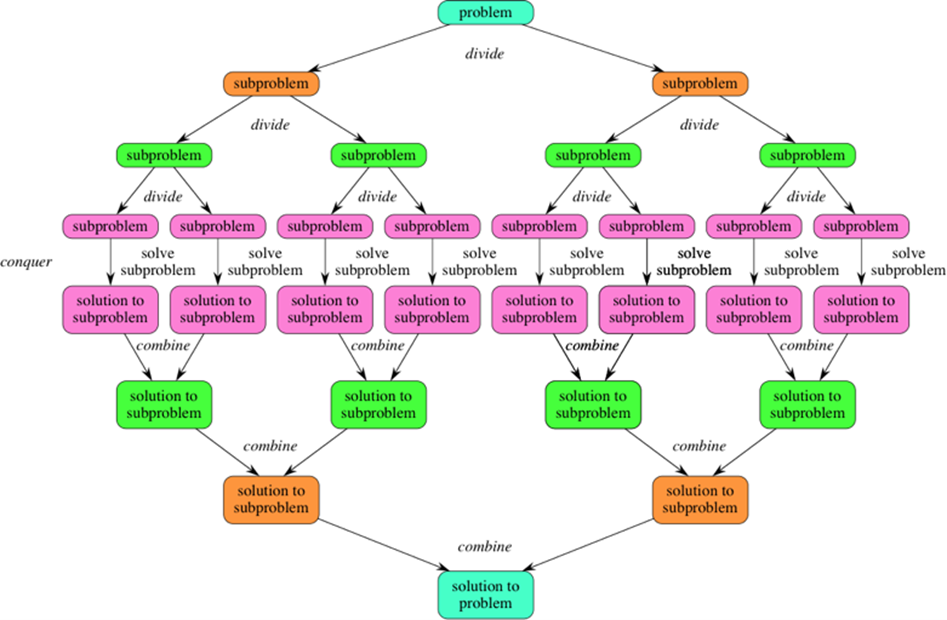
El algoritmo de "divide y vencerás" es una técnica de diseño algorítmico que se utiliza para resolver problemas complejos al descomponerlos en subproblemas más pequeños, más fáciles de resolver. La idea central es dividir el problema principal en subproblemas más simples, resolverlos de forma independiente y luego combinar sus soluciones para obtener la solución al problema original.

Algunos de los ejemplos comunes en los que se aplica la técnica de "divide y vencerás" incluyen:

1. Ordenamiento: Algoritmos de ordenamiento como Merge Sort y Quick Sort utilizan esta técnica para dividir el arreglo en subarreglos, ordenarlos individualmente y luego combinarlos en un arreglo ordenado.

2. Multiplicación de matrices: El algoritmo de Strassen para multiplicación de matrices aplica "divide y vencerás" para dividir la multiplicación de matrices en subproblemas más pequeños.

3. Problemas de búsqueda en árboles o grafos: Algoritmos como el recorrido de árboles (por ejemplo, el recorrido inorden, preorden, postorden) y búsqueda binaria en árboles binarios de búsqueda (BST) aplican la técnica de "divide y vencerás" para explorar y procesar subárboles.

Esta técnica es valiosa porque puede ayudar a reducir la complejidad de tiempo de algoritmos y hacer que la solución sea más eficiente. Sin embargo, es importante elegir una estrategia de combinación adecuada y garantizar que los subproblemas sean realmente más simples de resolver que el problema original para que la técnica sea efectiva.

2. Descripción y visualización de espacio de búsqueda

En este caso, como haremos un bot para sudoku no haremos visualización del conjunto de datos. En su lugar, describiremos detalladamente lo siguiente:

• Espacio de búsqueda

• Estado inicial

• Estado Final

• Transiciones

• Representación

  • Atributos
  • Tipos de datos

• Representación mediante grafos

• Cálculos del tamaño

• Visualización

  • Gráfico de una porción representativa del espacio de búsqueda

2.1. Espacio de búsqueda

El espacio de búsqueda en un Sudoku 9x9 se refiere a la colección de posibles configuraciones y soluciones que se pueden alcanzar al intentar resolver el rompecabezas. En un Sudoku 9x9, tienes una cuadrícula de 9 filas y 9 columnas, que se divide en nueve subgrillas más pequeñas de 3x3.

Para describir el espacio de búsqueda en un Sudoku 9x9, consideremos que cada celda puede contener un número del 1 al 9, representando un posible candidato para esa posición. Por lo tanto, en la primera celda, por ejemplo, tienes 9 posibles opciones (números del 1 al 9), en la segunda también 9 opciones, y así sucesivamente. Para la segunda celda, debes tener en cuenta la restricción de que no se puede repetir ningún número en la misma fila, columna o subgrilla.

A medida que vayas resolviendo el Sudoku, algunas celdas pueden tener menos opciones a medida que se llenan otras celdas y se aplican las reglas del juego. Esto reduce el espacio de búsqueda, ya que se eliminan algunas opciones para cada celda.

2.2. Estado Inicial

El estado inicial de un Sudoku 9x9 es una cuadrícula vacía con algunas celdas prellenadas con números del 1 al 9 de acuerdo con las reglas del juego. Estas celdas prellenadas proporcionan el punto de partida para resolver el rompecabezas.

El objetivo es completar la cuadrícula llenando las celdas vacías de manera que cada fila, cada columna y cada subgrilla de 3x3 contengan todos los números del 1 al 9 sin repeticiones.

2.3. Estado Final

El estado final es la configuración completa y correcta del Sudoku, donde todas las celdas están llenas y cumplen las reglas del juego.

En el estado final, todas las celdas están llenas y cumplen con las reglas del Sudoku, proporcionando una solución única para el rompecabezas. Cada fila, cada columna y cada subgrilla de 3x3 contiene todos los números del 1 al 9 sin repeticiones.

2.4. Transiciones

En el contexto del Sudoku de 9 x 9, las transiciones se refieren a los movimientos que se hacen para avanzar en la resolución del rompecabezas, es decir, cómo se llenan las celdas vacías siguiendo las reglas del juego. Estas transiciones están gobernadas por las reglas del Sudoku y la lógica que dicta cómo se deben completar las celdas. A continuación describiremos las principales transiciones utilizadas en sudoku:

Asignación de números iniciales: Al comienzo del juego, algunos números ya están dados y se colocan en ciertas celdas. Estos números iniciales se basan en la configuración inicial del Sudoku y son puntos de partida esenciales.

Identificación de números únicos: Se buscan filas, columnas o subgrillas en las que solo falta un número para completarlas. Se identifican las celdas donde solo hay una opción posible para ese número y se llena.

Eliminación de candidatos: A medida que se llenan las celdas, se eliminan esos números como candidatos válidos para las celdas de la misma fila, columna y subgrilla. Esto reduce las opciones en otras celdas y simplifica el proceso de resolución.

Técnicas de exclusión: Se utilizan técnicas de exclusión para identificar candidatos en celdas basándose en la presencia o ausencia de números en filas, columnas y subgrillas. Si un número solo puede ir en una celda en una fila, columna o subgrilla, se coloca en esa celda.

Comprobación de restricciones: En todo momento, se verifica que se cumplan las restricciones del Sudoku, es decir, que no haya números repetidos en filas, columnas o subgrillas.

Bifurcación: Si no se puede avanzar mediante técnicas de lógica y exclusión, a veces es necesario hacer una suposición educada sobre un número en una celda y continuar desde allí. Si esta suposición conduce a una contradicción (un conflicto con las reglas), se retrocede y se prueba otra suposición hasta encontrar una solución.

Retroceso (backtracking): Si una suposición lleva a una contradicción o a un Sudoku no válido, se retrocede a la suposición anterior y se prueba una nueva suposición. Esto se repite hasta encontrar una solución válida o descartar la suposición actual.

2.5. Representación

La representación es que tipos de estructuras de datos hemos utilizado para la elaboración del bot de sudoku de 9 x 9. A continuación, mostraremos las estructuras de datos que hemos usado y que estamos evaluando para el producto final.

• Matriz bidimensional NumFilas: Representa el tablero del Sudoku, donde cada celda contiene un número del 0 al 9. Un 0 indica una celda vacía que debe llenarse durante la resolución.

  En la función resultado, se realiza un recorrido por la matriz bidimensional NumFilas utilizando bucles for anidados para explorar y llenar las celdas vacías con números que cumplen las reglas del Sudoku.

  El algoritmo de backtracking intenta colocar números en las celdas vacías, verificando si es posible según las reglas del Sudoku. Si se encuentra una contradicción, se retrocede y se prueba con otro número hasta encontrar una solución válida.

	#Funcion resultado
	 def resultado(self):
	    for y in range(9):
		for x in range(9):
		    if self.NumFilas[y][x] == 0:
			for n in range(1, 10):
			    if self.verificacion(x, y, n):
				self.NumFilas[y][x] = n
				self.resultado()
				self.NumFilas[y][x] = 0
			return
	    self.imprimirNumFilas()
	    input("Seguimos?")

• Además de la matriz NumFilas, también se utilizan listas temporales y strings para manipular y presentar la información en la interfaz gráfica usando PyAutoGUI.

  Las funciones y su relación con estas estructuras de datos son las siguientes:

  verificacion, verificar_fila, verificar_columna y verificar_subcuadricula utilizan la matriz NumFilas, además del divide y vencerás para separar la función en métodos más pequeños, para verificar si colocar un número en una celda es válido de acuerdo con las reglas del Sudoku.

	def verificacion(self, x, y, n):
	  return (
	      self.verificar_fila(x, y, n) and
	      self.verificar_columna(x, y, n) and
	      self.verificar_subcuadricula(x, y, n)
	  )
	
	def verificar_fila(self, x, y, n):
	  for i in range(9):
	      if self.NumFilas[i][x] == n and i != y:
		  return False
	  return True
	
	def verificar_columna(self, x, y, n):
	  for i in range(9):
	      if self.NumFilas[y][i] == n and i != x:
		  return False
	  return True
	
	def verificar_subcuadricula(self, x, y, n):
	
	  x0 = (x // 3) * 3
	  y0 = (y // 3) * 3
	
	  for i in range(y0, y0 + 3):
	      for j in range(x0, x0 + 3):
		  if self.NumFilas[i][j] == n:
		      return False
	  return True

resultado utiliza la matriz NumFilas para buscar soluciones recursivamente y llenar las celdas vacías del Sudoku.

	def resultado(self):
	  for y in range(9):
	      for x in range(9):
		  if self.NumFilas[y][x] == 0:
		      for n in range(1, 10):
			  if self.verificacion(x, y, n):
			      self.NumFilas[y][x] = n
			      self.resultado()
			      self.NumFilas[y][x] = 0
		      return
	  self.imprimirNumFilas()
	  input("Seguimos?")

imprimirNumFilas crea estructuras temporales (final, str_fin, borde) para imprimir visualmente el Sudoku en la interfaz gráfica utilizando PyAutoGUI.

	def imprimirNumFilas(self):
	  final = list()
	  str_fin = list()
	  borde = list()
	
	  for i in range(9): final.append(self.NumFilas[i])
	
	  for listas in final:
	      for num in listas: str_fin.append(str(num))
	
	  for num in str_fin:
	      pg.press(num)
	      pg.hotkey('right')
	      borde.append(num)
	
	      longitud = len(borde)
	      if longitud % 9 == 0:
		  for i in range(9):
		      pg.hotkey('left')
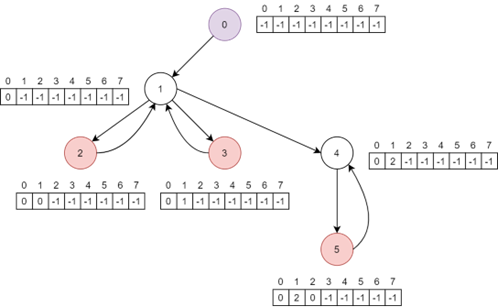
		  pg.hotkey('down')

2.6. Representación mediante grafos

Representar un sudoku mediante un grafo es posible utilizando una estructura de datos que modele las relaciones entre los elementos del sudoku de manera adecuada. Una forma común de hacerlo es utilizando un grafo bipartito, donde hay dos conjuntos de vértices: uno para las celdas del sudoku y otro para los números posibles en cada celda.

A continuación daremos un enfoque general para representar un sudoku como un grafo:

• Crear vértices para celdas y números:

Cada celda del sudoku se representa como un vértice en un conjunto. Cada número posible en cada celda también es un vértice, en otro conjunto.

• Establecer aristas entre celdas y números:

Para cada celda, conectarla con los números posibles para esa celda. También puedes conectar las celdas que están en la misma fila, columna y bloque (subgrids 3x3 en un sudoku clásico) entre sí.

2.7. Cálculos de tamaño

En un Sudoku 9x9, cada celda puede contener un número del 1 al 9 (inclusive) o puede estar vacía. Así, en una celda, hay 9 posibles opciones de número más la opción de estar vacía, lo que da un total de 10 posibles estados para cada celda.

Dado que un Sudoku 9x9 tiene 81 celdas (9 filas x 9 columnas), podemos calcular el tamaño del espacio de búsqueda multiplicando las posibilidades en cada celda:

10⁸¹

Esto es igual a 10⁸¹ o 1 seguido de 81 ceros, lo que es una cantidad astronómicamente grande. Es importante destacar que la mayoría de estas configuraciones no son soluciones válidas, ya que no cumplen con las reglas del Sudoku (no contienen números únicos en cada fila, columna y subgrilla de 3x3).

El resolver un Sudoku implica reducir este espacio de búsqueda, utilizando reglas y lógica para eliminar configuraciones inválidas y encontrar la solución correcta. Las técnicas de resolución buscan simplificar y acotar este espacio de búsqueda de manera eficiente para llegar a la solución correcta.

2.8. Visualización

Antes de pasar con el gráfico, es bueno explicar cómo es que podríamos llegar a calcular el espacio de búsqueda.

La fórmula para calcular el espacio de búsqueda en un Sudoku de tamaño n x n, donde cada celda puede contener números del 1 al n, se puede expresar como:

E = (n!)ⁿ²

donde:

• E es el tamaño del espacio de búsqueda.

• n es el tamaño de cada lado del Sudoku (por ejemplo, n = 9 para un Sudoku 9x9).

• n² es el número total de celdas en el Sudoku.

• n! es el factorial de n, que representa el número de formas en que puedes organizar los números del 1 al n en una fila o columna sin repetir ninguno.

• La fórmula se deriva de la multiplicación del número de permutaciones posibles para llenar cada fila y columna (que es n!) elevado a la potencia del total de celdas (n²).

2.8.1. Gráfico de una porción representativa del espacio de búsqueda

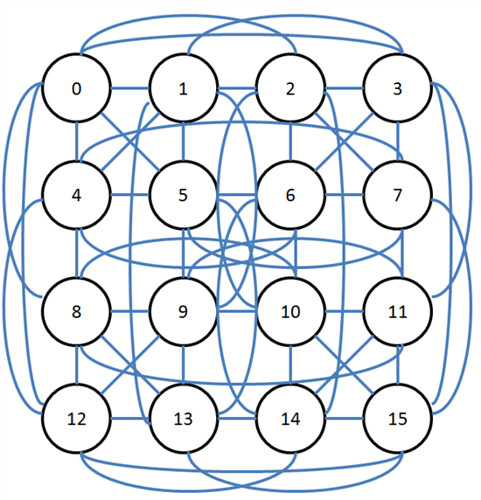
A continuación mostraremos un gráfico mínimo, el cual, representa el espacio de búsqueda mínimo que requiere nuestro sudoku.

3. Propuesta

• Debemos representar el Sudoku 16x16 en una estructura de datos adecuada. Utilizaremos una matriz 2D para representar el tablero, donde cada celda puede contener un número del 1 al 16. También es importante representar los números iniciales (pistas) y las celdas vacías.

• Desarrollaremos una función que verificará si un número se puede colocar en una celda en función de las reglas del Sudoku. Esto incluye verificar la fila, la columna y el bloque 4x4 al que pertenece la celda.

• Utilizaremos el algoritmo de backtracking para resolver el Sudoku. Comenzaremos en la primera celda vacía y, para cada celda, probaremos colocar un número válido (1-16). Luego, recursivamente, procederemos a la siguiente celda. Si llegamos a una celda donde no podemos colocar ningún número válido, retrocederemos (backtrack) a la celda anterior y probaremos con el siguiente número. Continuaremos este proceso hasta que hayamos llenado todo el tablero.

• Para mejorar la eficiencia de nuestra solución, utilizaremos el enfoque de divide y vencerás. Dividiremos el tablero en subgrids más pequeños, por ejemplo, en cuatro subgrids de 8x8, y luego resolveremos cada uno de ellos utilizando el algoritmo de backtracking. Esto simplificará el proceso y reducirá el tiempo de resolución.

• Además, implementaremos algunas optimizaciones. Utilizaremos técnicas de propagación para eliminar números inválidos en las celdas restantes, lo que reducirá la cantidad de backtracking necesario. Elegiremos las celdas vacías de manera inteligente, comenzando por las celdas con menos opciones válidas. También consideraremos el uso de algoritmos de búsqueda heurística como el algoritmo DLX (Dancing Links) para resolver Sudokus de manera eficiente.

• Finalmente aseguraremos de probar nuestro programa con varios Sudokus 16x16 para verificar su eficiencia y corrección.

4. Diseño de la aplicación

4.1. Análisis de requisitos

• El programa debe tener la capacidad de resolver sudokus
• Los algoritmos que se utilizarán serán backtracking y divide y vencerás
• La entrada de datos será manual para cada fila del sudoku
• La visualización de la resolución será al presionar un clic en la página del sudoku
• Los límites del algoritmo serán hasta los sudokus de dimensiones mayores a 16x16
• Se pueden presentar problemas de rendimiento al querer resolver los sudokus 16x16 debido a la mayor cantidad de dígitos que se deben emparejar para cumplir las reglas

4.2. Especificación

Estructuras utilizadas:

• Matriz para representar el tablero del sudoku

• Grafo para representar la matriz

Algoritmos utilizados:

• Backtracking para hallar las posible soluciones del sudoku avanzando y retrocediendo
• Divide y vencerás para separar las funcionalidades del programa

4.3. Diseño y arquitectura

• El main llama a las clases sudoku_solver, el cual posee el algoritmo de la solución del sudoku; de igual forma se incorpora la clase sudoku_printer, el cual imprime los numeros del sudoku al momento de rellenarse.

• El tablero del Sudoku se representa como una matriz bidimensional internamente en Python, donde cada celda puede contener un número del 1 al 9 (para un tablero de 9x9) o del 1 al 16 (para un tablero de 16x16).

• Las celdas vacías se representan comúnmente con el número 0 o el valor None.

• Se implementan funciones para verificar si un número ingresado por el jugador es válido en una celda específica, de acuerdo con las reglas del Sudoku. Esto asegura que el jugador no coloque números incorrectos en el tablero.

• Se puede implementar un algoritmo de resolución de Sudoku, como el algoritmo de backtracking, que permita a los jugadores resolver automáticamente el Sudoku o genere tableros válidos para el juego.

• Hemos realizado el GUI de la aplicación, el cual permite ingresar un sudoku ya creado por una página web y generar la solución de acuerdo a lo que solicita el requisito. Además al presionar en el sudoku generado, el código automáticamente generará un sudoku en la página mediante nuestro bot al presionar clic en la primera casilla.

  • Ejemplo de la interfaz creada con tkinter:

    

    
    
  • Sudoku siendo resuelto por el bot:

    

4.4. Programación

Lenguaje de programación: Se utiliza para desarrollar el algoritmo en Python versión 3.11.3 en adelante.

Bibliotecas: Se utilizan las siguientes bibliotecas en Python:

Time: Proporciona funciones relacionadas con el tiempo y la medición del tiempo. Permite a los programadores realizar tareas como medir el tiempo que lleva ejecutar una parte específica de un programa, crear retrasos o pausas en la ejecución de un programa y trabajar con marcas de tiempo.

Pyautogui: Es una biblioteca que permite la automatización de tareas en el sistema operativo y la interacción con la interfaz gráfica de usuario (GUI). Es especialmente útil para automatizar tareas repetitivas que implican el control del mouse y el teclado.

Numpy: Es una poderosa biblioteca para la computación numérica en Python. Proporciona estructuras de datos eficientes para trabajar con arreglos multidimensionales (matrices y vectores) y una amplia variedad de funciones matemáticas para realizar operaciones en estos arreglos.

Imagénes del código: Se presentan las siguiente imágenes

• Uso del backtracking

	def resultado(self):
	  for y in range(9):
	      for x in range(9):
		  if self.NumFilas[y][x] == 0:
		      for n in range(1, 10):
			  if self.verificacion(x, y, n):
			      self.NumFilas[y][x] = n
			      self.resultado()
			      self.NumFilas[y][x] = 0
		      return
	  self.imprimirNumFilas()
	  input("Seguimos?")

• Uso de divide y venceras

	def verificacion(self, x, y, n):
	  return (
	      self.verificar_fila(x, y, n) and
	      self.verificar_columna(x, y, n) and
	      self.verificar_subcuadricula(x, y, n)
	  )
	
	def verificar_fila(self, x, y, n):
	  for i in range(9):
	      if self.NumFilas[i][x] == n and i != y:
		  return False
	  return True
	
	def verificar_columna(self, x, y, n):
	  for i in range(9):
	      if self.NumFilas[y][i] == n and i != x:
		  return False
	  return True
	
	def verificar_subcuadricula(self, x, y, n):
	
	  x0 = (x // 3) * 3
	  y0 = (y // 3) * 3
	
	  for i in range(y0, y0 + 3):
	      for j in range(x0, x0 + 3):
		  if self.NumFilas[i][j] == n:
		      return False
	  return True

• Uso de la interfaz gráfica

	import tkinter as tk
from tkinter import ttk
from sudoku_solver import SudokuSolver
from sudoku_printer import SudokuPrinter
import time

class SudokuGUI:

    def __init__(self, root):
        self.root = root
        self.root.title("Sudoku Solver")
        self.sudoku_solver = SudokuSolver()
        self.sudoku_printer = SudokuPrinter()
        self.root.geometry("540x500+300+100")

        self.button_font = ('Arial', 14)
        self.title_font = ('Arial', 24, 'bold')
        self.create_widgets()

    def create_widgets(self):
        self.root.configure(bg='black')

        space_frame = tk.Frame(self.root, height=10, bg='black')
        space_frame.pack()

        self.style = ttk.Style()

        self.style.configure('TEntry', background='white', foreground='black', font=('Arial', 14))

        self.sudoku_frame = tk.Frame(self.root, bg='black')
        self.sudoku_frame.pack()

        for i in range(9):
            for j in range(9):
                entry = tk.Entry(self.sudoku_frame, width=3, bg='white', fg='black', font=('Arial', 14), bd=2)
                entry.grid(row=i, column=j, ipadx=10, ipady=10)
        
        solve_button = tk.Button(self.root, text="Resolver Sudoku", command=self.solve_sudoku, bg='darkgreen', fg='white', font=self.button_font)
        solve_button.pack(pady=10)

    def get_sudoku_input(self):
        num_filas = []
        for i in range(9):
            row_values = []
            for j in range(9):
                entry = self.sudoku_frame.grid_slaves(row=i, column=j)[0]
                value = entry.get()
                if value.isdigit():
                    row_values.append(int(value))
                else:
                    row_values.append(0)
            num_filas.append(row_values)
        return num_filas

    def solve_sudoku(self):
        numero_filas = self.get_sudoku_input()
        self.sudoku_solver.NumFilas = numero_filas

        time.sleep(1)
        self.sudoku_solver.resultado()

4.5. Análisis de complejidad

Análisis de Complejidad del Algoritmo de Backtracking: La complejidad del algoritmo de backtracking para resolver Sudoku depende de varios factores, incluyendo el tamaño del Sudoku y la disposición de los números iniciales.

Peor caso: En el peor caso, el algoritmo probará todas las combinaciones posibles hasta encontrar la solución correcta. La complejidad en el peor caso es exponencial y se estima como O(9^(n^2)), donde n es el tamaño de un lado del tablero Sudoku (por ejemplo, n=9 para un Sudoku de 9x9).

Caso promedio y mejor caso: La complejidad en casos promedio y mejores casos puede variar según la disposición inicial de los números. Sin embargo, en la práctica, el algoritmo de backtracking es altamente eficiente para la resolución de Sudokus.

Análisis de Complejidad del Algoritmo "Divide y Vencerás": Peor caso: La complejidad del algoritmo "divide y vencerás" para resolver Sudoku es O(9^n), donde n es el tamaño del lado del tablero del Sudoku. Este análisis es similar al del algoritmo de backtracking.

Caso promedio y mejor caso: El análisis en estos casos es similar al peor caso, ya que en última instancia, el algoritmo debe probar todas las combinaciones posibles.

En general, ambos enfoques, backtracking y "divide y vencerás", son altamente eficaces para resolver Sudokus, pero el enfoque de backtracking es ampliamente preferido y utilizado en la práctica debido a su simplicidad y eficiencia.

5. Validación de resultados y pruebas

• A continuación se presentarán los resultados de la ejecución del programa.

  5.1. Análisis de los resultados

  • ¿Cómo se ingresan las filas?:

    Para ingresar las filas se debe ingresar los números de izquierda a derecha, en una página web de sudoku 9 x 9.

  
  

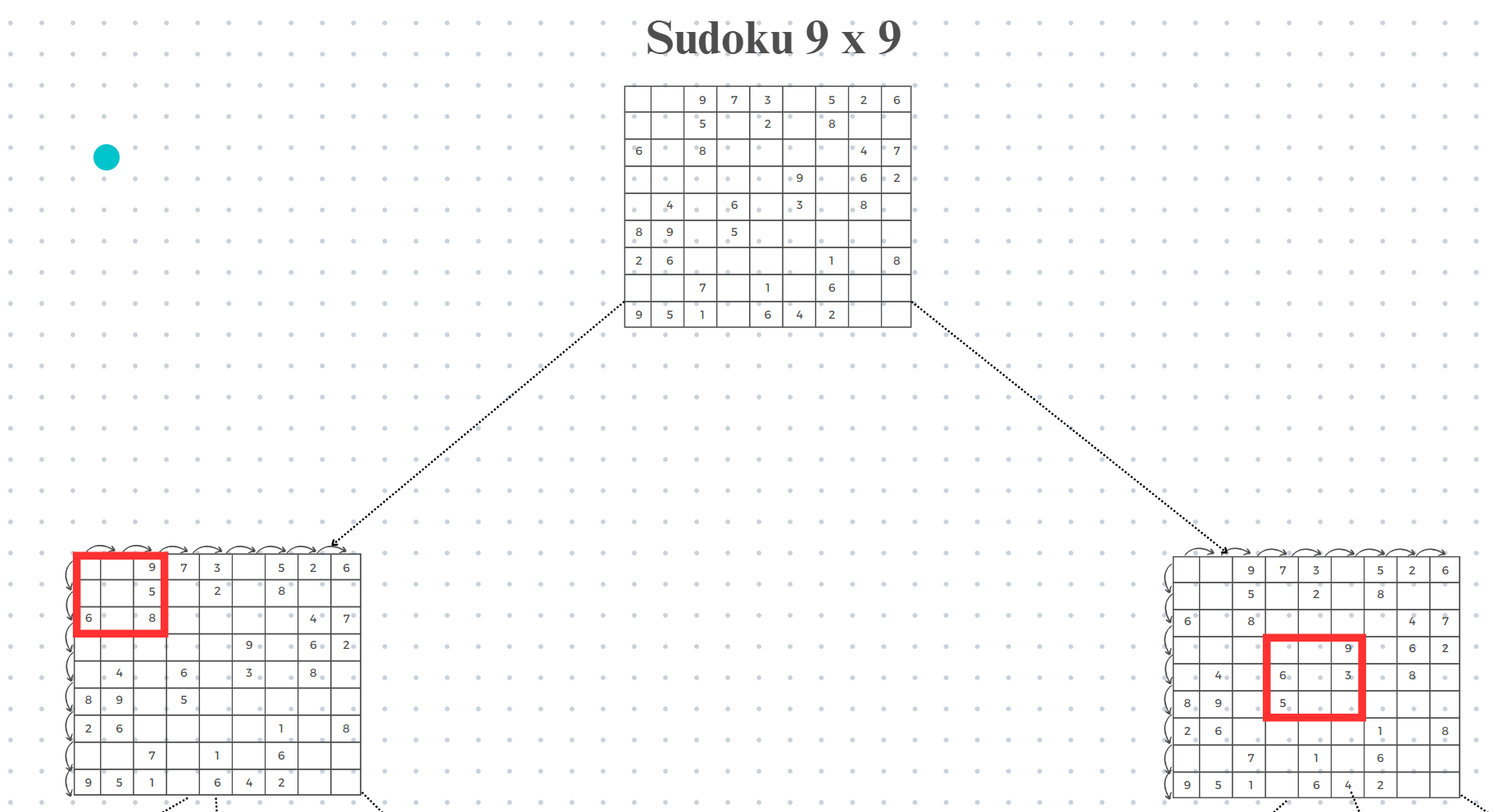
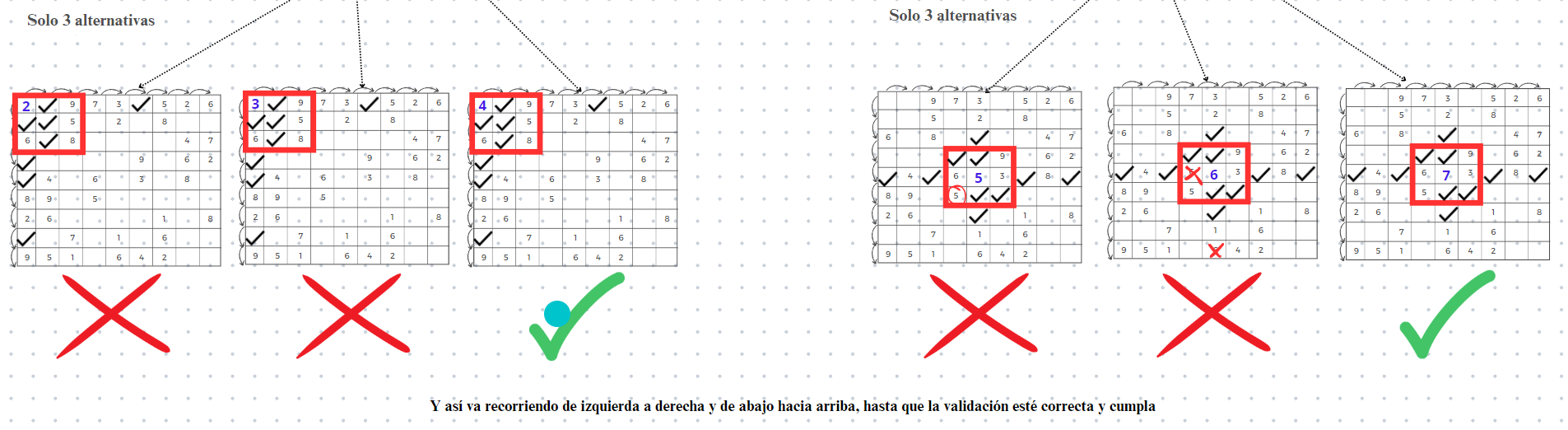
- Datos de entrada: Podemos observar en el ejemplo de abajo que se debe ingresar las 9 filas que conforman el sudoku de 9 x 9, el cual se conforma de 1 a 9 y los 0 se representan como espacios en blanco.

- Datos de salida: Podemos observar que al ingresar las variables, solo basta con hacer clic en la página del sudoku para que se resuelva con el bot hecho. En este ejemplo, puede visualizar el algoritmo de backtracking, el cual se puede observar que se va retrocediendo hasta encontrar la solución correcta y va comparando hasta que el algoritmo simplemente lo haya terminado de solucionar.

Finalmente, aparace un mensaje de "Excelente" o por defecto un mensaje, el cual indica que el sudoku ha sido resuelto correctamente. Esto puede ser corroborado en cualquier sudoku de 9 x 9 en internet.

6. Conclusiones

• Resolver un Sudoku de 16x16 es significativamente más complejo que resolver un Sudoku estándar de 9x9. El aumento en el tamaño del tablero aumenta exponencialmente la cantidad de combinaciones posibles y, por lo tanto, la dificultad del problema.

  
  

• El algoritmo de backtracking es esencial para resolver Sudokus, ya que permite explorar diferentes posibilidades en busca de la solución correcta. Sin embargo, para Sudokus 16x16, la cantidad de retrocesos puede ser muy alta debido a la mayor complejidad del problema.

  
  

• La estrategia de divide y vencerás es útil para optimizar el proceso de resolución. Se divide el tablero en subgrids más pequeños, resolverlos por separado y luego combinar las soluciones parciales. Esto reduce la cantidad de ramificaciones en el árbol de búsqueda

  
  

• La eficiencia del algoritmo es crucial para resolver Sudokus de manera práctica, especialmente en tamaños grandes. Se puede seguir mejorando la velocidad de resolución mediante técnicas de optimización.

  
  

• Los Sudokus 16x16 son propensos a errores y fallas debido a la mayor complejidad. Es importante implementar un manejo robusto de errores y un registro de las decisiones tomadas y los retrocesos realizados para depurar y mejorar el algoritmo.

  
  

• Para garantizar la calidad de tu algoritmo, debemos seguir realizando pruebas exhaustivas con una variedad de Sudokus de diferentes tamaños y niveles de dificultad. Esto te ayudará a identificar posibles fallos y a optimizar el rendimiento.

7. Bibliografía

Ekström, J., & Pitkäjärvi, K. (2015). "The backtracking algorithm and different representations for solving Sudoku Puzzles."

Sánchez, A. (12 de mayo de 2022). La librería Numpy. Aprende con Alf. https://aprendeconalf.es/docencia/python/manual/numpy/

Recursos Python (2 de junio de 2017). PyAutoGUI – Módulo de automatización multiplataforma. Recursos Python. https://recursospython.com/guias-y-manuales/pyautogui/

Bartolomé, M. (29 de marzo de 2019). Fecha y hora: la biblioteca time. Mclibre. https://www.mclibre.org/consultar/python/lecciones/python-biblioteca-time.html

Geeksforgeeks (27 de julio de 2013). Backtracking Algorithms. Geeksforgeeks. https://www.geeksforgeeks.org/backtracking-algorithms/

Cormen, T., Balkcom, D.(2014). Algoritmos de divide y vencerás. Khan Academy. https://es.khanacademy.org/computing/computer-science/algorithms/merge-sort/a/divide-and-conquer-algorithms