Code developed in SAS v9.4
Simulations used to estimate power for global rank composite versus decision rule, mimicking CITRIS-ALI.
The global rank
Global Rank is a generic term encompassing a number of composites. The intention is to assign every patient a rank among the other patients that summarises their response.
The following equation describes the calculation.
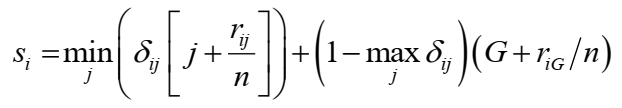
where n is the total sample size, G is the total number of outcomes, δij=1 if patient i failed on outcome j and 0 otherwise, and rij is the rank for patient i on outcome j (rank 1 being the worst response and n being the best).
The global rank composite is promoted in the medical literature. For example, see:
- Califf 1990: Left Ventricular Ejection Fraction May Not Be Useful as an End Point of Thrombolytic Therapy Comparative Trials
- Felker & Maisel 2010: A Global Rank End Point for Clinical Trials in Acute Heart Failure
- Packer 2016: Development and Evolution of a Hierarchical Clinical Composite End Point for the Evaluation of Drugs and Devices for Acute and Chronic Heart Failure
Simulations and power estimation
Input required for each outcome includes a base rate, effect due to intervention, and correlations among outcomes (although from our experience, correlations often have an unimportant effect on power estimates).
We must also specify the order of outcomes for the hierarchy and cut-offs defining when to move to the next outcome (i.e. according to "failure").
- Effect sizes and initial working correlations can be found in simul_data.sas
- Ordering of outcomes and cut-offs can be found in derive_GR.sas
For our simulations we used moderate effect sizes:
- Control, base rate:
SOFA score at 96 hours: 7
CRP (ug/mL) at 168 hours: 40
Thrombomodulin (ng/mL) at 168 hours: 12
Mortality at Day 28: 0.25 - Intervention, change:
SOFA score at 96 hours: -1
CRP (ug/mL) at 168 hours: -5
Thrombomodulin (ng/mL) at 168 hours: -2
Mortality at Day 28: -0.02
These guesstimates are based on:
- VITAMINS: Effect of Vitamin C, Hydrocortisone, and Thiamine vs Hydrocortisone Alone on Time Alive and Free of Vasopressor Support Among Patients With Septic Shock
- CITRIS-ALI: Effect of Vitamin C Infusion on Organ Failure and Biomarkers of Inflammation and Vascular Injury in Patients With Sepsis and Severe Acute Respiratory Failure
The assumed effect estimates, cut-offs etc. can be modified to evaluate the effect this has on the power estimates. For further information, see Power and Sample Size Estimation for Composite Endpoints: Practical Implementation using Data Simulations
16jun2021, NOTE: there is likely a better way, now, to achieve the desired correlations when simulating the random variables: https://blogs.sas.com/content/iml/2021/06/14/simulate-iman-conover-transformation.html