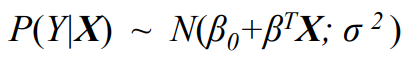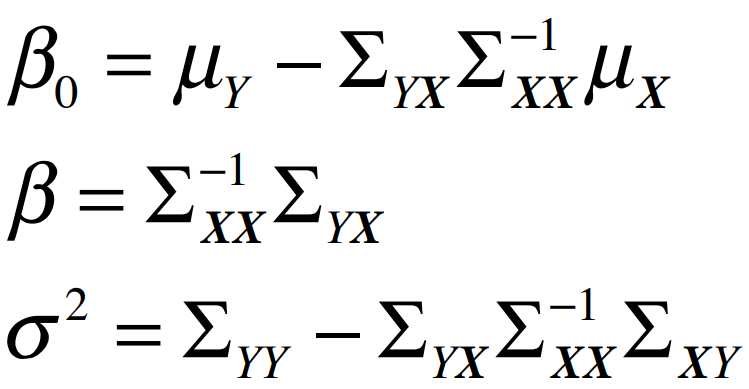Linear Gaussian Bayesian Networks -Representation, Learning and Inference

A Bayesian Network (BN) is a probabilistic graphical model that represents a set of variables and their conditional dependencies via graph. Gaussian BN is a special case where set of continuous variables are represented by Gaussian Distributions. Gaussians are surprisingly good approximation for many real world continuous distributions.

This package helps in modelling the network, learning parameters through data and running inference with evidence(s). Two types of Gaussian BNs are implemented:

1. Linear Gaussian Network: A directed BN where CPDs are linear gaussian.

2. Gaussian Belief Propagation: An undirected BN where it runs message passing algorithm to iteratively solve precision matrix and find out marginals of variables with or without conditionals.

Installation

$ pip install lgnpy

or clone the repository.

$ git clone https://github.com/ostwalprasad/lgnpy

Getting Started

Here are steps for Linear Gaussian Network. Gaussian Belief Propagation Model is also similar.

1. Create Network

import pandas as pd
import numpy as np
from lgnpy import LinearGaussian

lg = LinearGaussian()
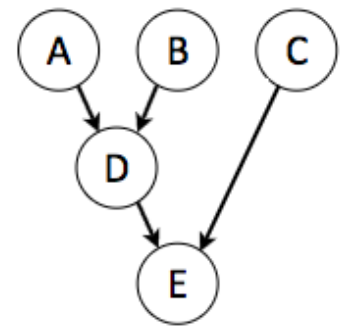
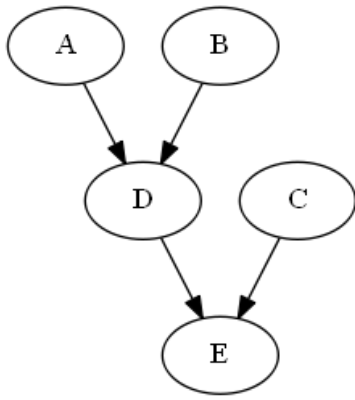
lg.set_edges_from([('A', 'D'), ('B', 'D'), ('D', 'E'), ('C', 'E')])

2 Create Data and assign to it to network.

​ Create synthetic data for network using pandas and bind network with the data. There's no need to separately calculate means and covariance matrix.

np.random.seed(42)
n=100
data = pd.DataFrame(columns=['A','B','C','D','E'])
data['A'] = np.random.normal(5,2,n)
data['B'] = np.random.normal(10,2,n)
data['D'] = 2*data['A'] + 3*data['B'] + np.random.normal(0,2,n)
data['C'] = np.random.normal(-5,2,n)
data['E'] = 3*data['C'] + 3*data['D'] + np.random.normal(0,2,n)

lg.set_data(data)

3. Set Evidence(s)

Evidence are optional and can be set before running inference.

 lg.set_evidences({'A':5,'B':10})

4. Run Inference

For each node, CPT (Conditional Probability Distribution) is defined as::

where, its parameters are calculated using conditional distribution of parent(s) and nodes:

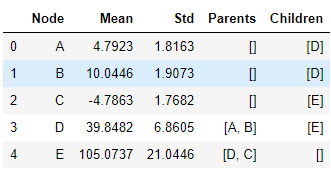
run_inference() returns inferred means and variances of each nodes.

lg.run_inference(debug=False)

Additional Functions:

lg.plot_distributions(save=False)

lg.network_summary()

lg.draw_network(filename='sample_network',open=True)

Examples

Notebook: Linear Gaussian Networks

Known Issues

GaussianBP algorithm does not converge for some specific precision matrices (inverse covariances). Solution is to use Graphcial Lasso or similar estimator methods to find precision matrix. Pull requests are welcome.

References:

Linear Gaussian Networks

1. Probabilistic Graphical Models - Principles and Techniques , Daphne Koller, Chapter 7.2

2. Gaussian Bayesian Networks, Sargur Srihari

Gaussian Belief Propagation

1. Probabilistic Graphical Models - Principles and Techniques , Daphne Koller, Chapter 14.2.3
2. Gaussian Belief Propagation: Theory and Aplication, Danny Bickson

Citation

If you use lgnpy or reference our blog post in a presentation or publication, we would appreciate citations of our package.

P. Ostwal, “ostwalprasad/LGNpy: v1.0.0.” Zenodo, 20-Jun-2020, doi: 10.5281/ZENODO.3902122.

Here is the corresponding BibText entry

@misc{https://doi.org/10.5281/zenodo.3902122,
  doi = {10.5281/ZENODO.3902122},
  url = {https://zenodo.org/record/3902122},
  author = {Ostwal,  Prasad},
  title = {ostwalprasad/LGNpy: v1.0.0},
  publisher = {Zenodo},
  year = {2020}
}

License

MIT License Copyright (c) 2020, Prasad Ostwal