CompassVerifier is an accurate and robust lightweight verifier model for evaluation and outcome reward. It demonstrates multi-domain competency spanning math, knowledge, and diverse reasoning tasks, with the capability to process various answer types, including multi-subproblems, formulas, and sequence answers, while effectively identifying abnormal/invalid/long-reasoning responses and robust to different prompt styles. We also introduce VerifierBench benchmark comprising question and model outputs collected from multiple data sources from about 1 million predictions from various common-used models and datasets, labeled by human experts.
We release the best performing model and dataset from our experiments. Pick a suitable model from the following table and download the model checkpoint.
| Dataset | HF Path |
|---|---|
| VerifierBench | 🤗 OpenCompass/VerifierBench |
| Model | HF Path |
|---|---|
| CompassVerifier-3B | 🤗 OpenCompass/CompassVerifier-3B |
| CompassVerifier-7B | 🤗 OpenCompass/CompassVerifier-7B |
| CompassVerifier-32B | 🤗 OpenCompass/CompassVerifier-32B |
git clone https://github.com/OpenCompass/CompassVerifier.git
cd CompassVerifier/srcUse the following code to verify the model, you can find the code in src/cv_eval.ipynb.
import re
from transformers import AutoTokenizer, AutoModelForCausalLM
from prompts import CV_PROMPT, CV_COT_PROMPT
test_sample = [
{
"question": "Harold tosses a nickel four times. What is the probability that he gets at least as many heads as tails?",
"gold_answer": "\\frac{11}{16}",
"llm_response": "Alright, I have this probability problem to solve:\n\n**Problem:** Harold tosses a nickel four times. What is the probability that he gets at least as many heads as tails?\n\nFirst, I need to understand what's being asked. Harold is tossing a nickel (which I assume is a fair coin) four times. I need to find the probability that the number of heads is at least as many as the number of tails.\n\n### Understanding the Problem\n\n- **Total number of tosses (n):** 4\n- **Coin:** Fair, so probability of heads (H) = probability of tails (T) = 0.5\n- **Desired outcome:** Number of heads ≥ number of tails\n\nSince there are four tosses, the number of heads can range from 0 to 4. The number of tails will then be 4 minus the number of heads.\n\nSo, the possible number of heads (k) and corresponding number of tails (4 - k) are:\n\n- k = 0: Tails = 4\n- k = 1: Tails = 3\n- k = 2: Tails = 2\n- k = 3: Tails = 1\n- k = 4: Tails = 0\n\nWe need the number of heads to be at least as many as the number of tails, i.e., k ≥ 4 - k.\n\nLet's solve the inequality:\n\nk ≥ 4 - k \nk + k ≥ 4 \n2k ≥ 4 \nk ≥ 2\n\nSo, the number of heads must be 2, 3, or 4.\n\n### Calculating the Probabilities\n\nTo find the probability of getting at least as many heads as tails, I need to calculate the probabilities for k = 2, 3, and 4 and then sum them up.\n\nThe probability of getting exactly k heads in n tosses of a fair coin is given by the binomial probability formula:\n\nP(k) = C(n, k) * (0.5)^n\n\nWhere:\n- C(n, k) is the number of combinations of n items taken k at a time.\n- (0.5)^n is the probability of any specific sequence of n tosses.\n\nSince the coin is fair, (0.5)^n will be the same for all k, so we can factor that out when summing the probabilities.\n\nBut to simplify, I'll calculate each probability separately.\n\n#### 1. Probability of getting exactly 2 heads (k = 2)\n\nC(4, 2) = 6 \nP(2) = 6 * (0.5)^4 = 6 * 0.0625 = 0.375\n\n#### 2. Probability of getting exactly 3 heads (k = 3)\n\nC(4, 3) = 4 \nP(3) = 4 * (0.5)^4 = 4 * 0.0625 = 0.25\n\n#### 3. Probability of getting exactly 4 heads (k = 4)\n\nC(4, 4) = 1 \nP(4) = 1 * (0.5)^4 = 1 * 0.0625 = 0.0625\n\n### Summing the Probabilities\n\nNow, I'll sum the probabilities for k = 2, 3, and 4:\n\nP(at least as many heads as tails) = P(2) + P(3) + P(4) \n= 0.375 + 0.25 + 0.0625 \n= 0.6875\n\n### Verifying the Calculation\n\nTo ensure I didn't make a mistake, I'll double-check the calculations:\n\n- **C(4, 2) = 6** ✔️\n- **C(4, 3) = 4** ✔️\n- **C(4, 4) = 1** ✔️\n- **(0.5)^4 = 0.0625** ✔️\n- **0.375 + 0.25 + 0.0625 = 0.6875** ✔️\n\nEverything seems to add up correctly.\n\n### Final Answer\n\nThe probability that Harold gets at least as many heads as tails when tossing a nickel four times is:\n\n\\boxed{0.6875}",
"gold_judgment": "A"
},
{
"question": "Factor completely over the set of polynomials with integer coefficients:\n\\[x^4 - 4x^3 + 14x^2 - 4x + 13.\\]",
"gold_answer": "(x^2 + 1)(x^2 - 4x + 13)",
"llm_response": "To factor the polynomial $x^4 - 4x^3 + 14x^2 - 4x + 13$ completely over the set of polynomials with integer coefficients, we will follow these steps:\n\n1. **Check for possible rational roots**: Use the Rational Root Theorem, which states that any rational root, expressed as a fraction $\\frac{p}{q}$, must have $p$ as a factor of the constant term (13) and $q$ as a factor of the leading coefficient (1). The possible rational roots are $\\pm1, \\pm13$.\n\n2. **Test the possible rational roots**: Substitute each possible rational root into the polynomial to check if it equals zero.\n\nLet's start by testing $x = 1$:\n$$\n1^4 - 4 \\cdot 1^3 + 14 \\cdot 1^2 - 4 \\cdot 1 + 13 = 1 - 4 + 14 - 4 + 13 = 20 \\neq 0\n$$\nSo, $x = 1$ is not a root.\n\nNext, test $x = -1$:\n$$\n(-1)^4 - 4 \\cdot (-1)^3 + 14 \\cdot (-1)^2 - 4 \\cdot (-1) + 13 = 1 + 4 + 14 + 4 + 13 = 36 \\neq 0\n$$\nSo, $x = -1$ is not a root.\n\nNext, test $x = 13$:\n$$\n13^4 - 4 \\cdot 13^3 + 14 \\cdot 13^2 - 4 \\cdot 13 + 13\n$$\nThis value is extremely large and clearly not zero.\n\nNext, test $x = -13$:\n$$\n(-13)^4 - 4 \\cdot (-13)^3 + 14 \\cdot (-13)^2 - 4 \\cdot (-13) + 13\n$$\nThis value is also extremely large and clearly not zero.\n\nSince none of the possible rational roots are actual roots, we proceed to other methods.\n\n3. **Grouping and factoring by grouping**: This method is not directly applicable here since the polynomial is a quartic and does not factor neatly into quadratic pairs.\n\n4. **Using substitution or known identities**: Sometimes, quartic polynomials can be transformed into quadratic polynomials using substitutions or identities. However, this polynomial does not appear to fit neatly into such categories.\n\n5. **Numerical or graphical methods**: For polynomials that do not factor easily, numerical methods or graphing can be used to approximate roots. However, since we are looking for integer coefficients, we need exact factors.\n\nGiven the complexity and the results from our initial checks, we conclude that the polynomial $x^4 - 4x^3 + 14x^2 - 4x + 13$ does not factor further over the set of polynomials with integer coefficients.\n\nThus, the final answer is:\n$$\n\\boxed{x^4 - 4x^3 + 14x^2 - 4x + 13}\n$$",
"gold_judgment": "B",
},
{
"question": "请你做一道数学选择题\n请你一步一步思考并将思考过程写在【解析】和<eoe>之间。你将从A,B,C,D中选出正确的答案,并写在【答案】和<eoa>之间。\n例如:【答案】: A <eoa>\n完整的题目回答的格式如下:\n【解析】 ... <eoe>\n【答案】 ... <eoa>\n请你严格按照上述格式作答。\n题目如下:8. (5 分) 设 $\\alpha \\in\\left(0, \\frac{\\pi}{2}\\right), \\beta \\in\\left(0, \\frac{\\pi}{2}\\right)$, 且 $\\tan \\alpha=\\frac{1+\\sin \\beta}{\\cos \\beta}$, 则()\nA. $3 \\alpha-\\beta=\\frac{\\pi}{2}$\nB. $3 \\alpha+\\beta=\\frac{\\pi}{2}$\nC. $2 \\alpha-\\beta=\\frac{\\pi}{2}$\nD. $2 \\alpha+\\beta=\\frac{\\pi}{2}$\n\n",
"gold_answer": "['C']",
"llm_response": "【解析】\n首先,我们从给定的条件 $\\tan \\alpha = \\frac{1 + \\sin \\beta}{\\cos \\beta}$ 开始分析。\n\n1. 使用三角恒等式,我们可以将 $\\frac{1 + \\sin \\beta}{\\cos \\beta}$ 进行分解:\n \\[\n \\frac{1 + \\sin \\beta}{\\cos \\beta} = \\frac{1}{\\cos \\beta} + \\frac{\\sin \\beta}{\\cos \\beta} = \\sec \\beta + \\tan \\beta\n \\]\n 因此,$\\tan \\alpha = \\sec \\beta + \\tan \\beta$。\n\n2. 我们知道 $\\sec \\beta = \\frac{1}{\\cos \\beta}$,所以可以将上式改写为:\n \\[\n \\tan \\alpha = \\frac{1}{\\cos \\beta} + \\frac{\\sin \\beta}{\\cos \\beta} = \\frac{1 + \\sin \\beta}{\\cos \\beta}\n \\]\n 这与原条件一致。\n\n3. 接下来,我们需要验证选项中的关系。我们从选项 D 开始验证:$2 \\alpha + \\beta = \\frac{\\pi}{2}$。\n\n4. 如果 $2 \\alpha + \\beta = \\frac{\\pi}{2}$,则 $\\beta = \\frac{\\pi}{2} - 2 \\alpha$。\n\n5. 将 $\\beta = \\frac{\\pi}{2} - 2 \\alpha$ 代入原条件 $\\tan \\alpha = \\frac{1 + \\sin \\beta}{\\cos \\beta}$ 中:\n \\[\n \\sin \\beta = \\sin \\left( \\frac{\\pi}{2} - 2 \\alpha \\right) = \\cos 2 \\alpha\n \\]\n \\[\n \\cos \\beta = \\cos \\left( \\frac{\\pi}{2} - 2 \\alpha \\right) = \\sin 2 \\alpha\n \\]\n\n6. 代入后得到:\n \\[\n \\tan \\alpha = \\frac{1 + \\cos 2 \\alpha}{\\sin 2 \\alpha}\n \\]\n\n7. 使用双角公式 $\\cos 2 \\alpha = 2 \\cos^2 \\alpha - 1$ 和 $\\sin 2 \\alpha = 2 \\sin \\alpha \\cos \\alpha$,我们得到:\n \\[\n \\tan \\alpha = \\frac{1 + 2 \\cos^2 \\alpha - 1}{2 \\sin \\alpha \\cos \\alpha} = \\frac{2 \\cos^2 \\alpha}{2 \\sin \\alpha \\cos \\alpha} = \\frac{\\cos \\alpha}{\\sin \\alpha} = \\cot \\alpha\n \\]\n\n8. 由于 $\\tan \\alpha = \\cot \\alpha$,这意味着 $\\alpha = \\frac{\\pi}{4}$。\n\n9. 代入 $\\alpha = \\frac{\\pi}{4}$ 回到 $\\beta = \\frac{\\pi}{2} - 2 \\alpha$,我们得到:\n \\[\n \\beta = \\frac{\\pi}{2} - 2 \\cdot \\frac{\\pi}{4} = \\frac{\\pi}{2} - \\frac{\\pi}{2} = 0\n \\]\n\n10. 但是 $\\beta$ 必须在 $(0, \\frac{\\pi}{2})$ 之间,因此 $\\alpha = \\frac{\\pi}{4}$ 不成立。\n\n11. 重新检查选项,发现选项 C 也可能是正确的。验证选项 C:$2 \\alpha - \\beta = \\frac{\\pi}{2}$。\n\n12. 如果 $2 \\alpha - \\beta = \\frac{\\pi}{2}$,则 $\\beta = 2 \\alpha - \\frac{\\pi}{2}$。\n\n13. 将 $\\beta = 2 \\alpha - \\frac{\\pi}{2}$ 代入原条件 $\\tan \\alpha = \\frac{1 + \\sin \\beta}{\\cos \\beta}$ 中:\n \\[\n \\sin \\beta = \\sin \\left( 2 \\alpha - \\frac{\\pi}{2} \\right) = -\\cos 2 \\alpha\n \\]\n \\[\n \\cos \\beta = \\cos \\left( 2 \\alpha - \\frac{\\pi}{2} \\right) = \\sin 2 \\alpha\n \\]\n\n14. 代入后得到:\n \\[\n \\tan \\alpha = \\frac{1 - \\cos 2 \\alpha}{\\sin 2 \\alpha}\n \\]\n\n15. 使用双角公式 $\\cos 2 \\alpha =",
"gold_judgment": "C"
}
]
def process_judgment(judgment_str: str) -> str:
# First try to find the exact \boxed{letter} pattern
boxed_matches = re.findall(r'boxed{([A-C])}', judgment_str)
if boxed_matches:
return boxed_matches[-1]
# Directly return the judgment if it is A, B, or C
if judgment_str in ["A", "B", "C"]:
return judgment_str
else:
final_judgment_str = judgment_str.split("Final Judgment:")[-1]
matches = re.findall(r'\(([A-C])\)*', final_judgment_str)
if matches:
return matches[-1]
matches = re.findall(r'([A-C])', final_judgment_str)
if matches:
return matches[-1]
return ""
# You can change the model name to "opencompass/CompassVerifier-7B" or "opencompass/CompassVerifier-32B"
model_name = "opencompass/CompassVerifier-3B"
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModelForCausalLM.from_pretrained(
model_name,
torch_dtype="auto",
device_map="auto"
)
for sample in test_sample:
model_input = CV_PROMPT.format(question=sample["question"], gold_answer=sample["gold_answer"], llm_response=sample["llm_response"])
messages=[{"role": "user", "content": model_input}]
input_text = tokenizer.apply_chat_template(
messages,
add_generation_prompt=True,
tokenize=False
)
model_inputs = tokenizer(input_text, return_tensors="pt").to(model.device)
output=model.generate(
**model_inputs,
do_sample=False,
max_new_tokens=2048)
judgement=tokenizer.decode(output[0][model_inputs.input_ids.shape[1]:],skip_special_tokens=True)
print("ori_judgment: ", judgement)
print("processed_judgment: ", process_judgment(judgement))
print("*"*100)outputs:
ori_judgment: A
processed_judgment: A
****************************************************************************************************
ori_judgment: B
processed_judgment: B
****************************************************************************************************
ori_judgment: C
processed_judgment: C
****************************************************************************************************
The output will only be A/B/C.
- A: correct
- B: incorrect
- C: the question or the response or the answer has serious quality problems (such as the question has ambiguity and is incomplete, the answer is incomplete or the model response is truncated and repeated, etc.)
⚠️ Currently, you can treat both B and C as incorrect labels.
You can also use the COT mode to increase the accuracy of the judgment for complex problems. Just use the CV_COT_PROMPT instead of CV_PROMPT. The outputs will be like this:
ori_judgment: Analysis step by step:
1. **Validity Check**:
- The candidate's answer is complete, not repetitive, and not a refusal. It provides a detailed explanation and arrives at a final answer.
2. **Question Requirements**:
- The question asks for the probability that Harold gets at least as many heads as tails when tossing a nickel four times. The standard answer is \(\frac{11}{16}\), which is approximately 0.6875.
3. **Comparison of Answers**:
- The candidate's final answer is \(\boxed{0.6875}\).
- The standard answer is \(\frac{11}{16}\), which is numerically equivalent to 0.6875.
- The candidate's answer matches the standard answer in both value and meaning, despite the difference in presentation (decimal vs. fraction).
4. **Numerical Precision**:
- The candidate's answer is precise and matches the standard answer when converted to decimal form.
Final Judgment: \boxed{A} - CORRECT
processed_judgment: A
****************************************************************************************************
ori_judgment: Analysis step by step:
1. **Validity Check**:
- The candidate's answer is complete, not repetitive, and not a refusal. It provides a detailed explanation and concludes with a final answer.
2. **Question Requirements**:
- The question asks to factor the polynomial completely over the set of polynomials with integer coefficients. The standard answer provides a factored form: \((x^2 + 1)(x^2 - 4x + 13)\).
3. **Comparison of Answers**:
- The candidate's final answer is \(x^4 - 4x^3 + 14x^2 - 4x + 13\), which is the original polynomial. This does not match the standard answer \((x^2 + 1)(x^2 - 4x + 13)\).
- The candidate concludes that the polynomial does not factor further, which contradicts the standard answer, which provides a complete factorization.
4. **Conclusion**:
- The candidate's answer does not match the standard answer. The standard answer provides a complete factorization, while the candidate claims the polynomial cannot be factored further.
Final Judgment: \boxed{B} - INCORRECT
processed_judgment: B
****************************************************************************************************
ori_judgment: Analysis step by step: [
1. First, check if the candidate's answer is INCOMPLETE, REPETITIVE, or a REFUSAL. The candidate's answer is cut off mid-sentence at step 15, specifically during the calculation of $\cos 2 \alpha$. Therefore, it is INCOMPLETE.
2. Since the answer is INCOMPLETE, we do not proceed to compare it with the standard answer.
]
Final Judgment: \boxed{C} - INCOMPLETE
processed_judgment: C
****************************************************************************************************
CompassVerifier is build from the Qwen series model, so you can also use inference framwork like vllm, lmdeploy or sglang to accelerate the inference speed, take vllm as a template:
# first install vllm
pip install vllm==0.8.5Then select a model to serve, and follow the instructions in the vllm doc to use the service.
vllm serve --model opencompass/CompassVerifier-3B --tensor-parallel-size 1 --max-model-len 2048or just infer locally:
from transformers import AutoTokenizer
from vllm import LLM, SamplingParams
from prompts import CV_PROMPT, CV_COT_PROMPT
model_name = "opencompass/CompassVerifier-3B"
tokenizer = AutoTokenizer.from_pretrained(model_name)
vllm_model = LLM(
model=model_name,
tensor_parallel_size=1
)
sampling_params = SamplingParams(
temperature=0.0,
max_tokens=2048
)
for sample in test_sample:
model_input = CV_PROMPT.format(
question=sample["question"],
gold_answer=sample["gold_answer"],
llm_response=sample["llm_response"]
)
messages = [{"role": "user", "content": model_input}]
model_inputs = tokenizer.apply_chat_template(
messages,
add_generation_prompt=True,
tokenize=False
)
outputs = vllm_model.generate([model_inputs], sampling_params)
judgement = outputs[0].outputs[0].text
print(judgement)
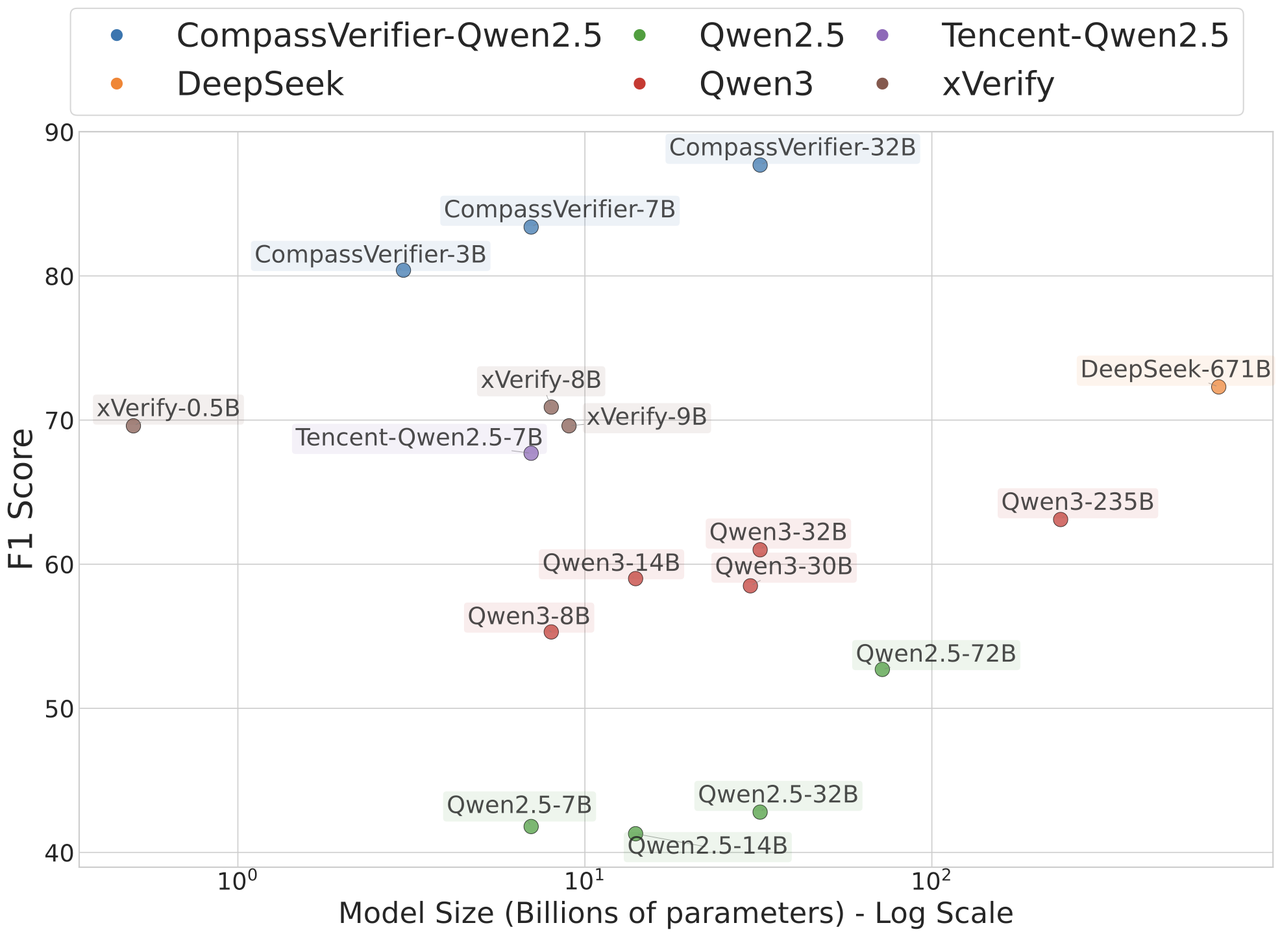
print("*" * 100)CompassVerifier performance (F1 score w/o COT) on our new released VerifierBench:
| Model | General Reasoning | Knowledge | Math | Science | AVG |
|---|---|---|---|---|---|
| General Models | |||||
| Qwen2.5-7B-Instruct | 51.1 | 50.7 | 30.0 | 36.6 | 42.1 |
| Qwen2.5-32B-Instruct | 42.2 | 46.4 | 31.6 | 48.8 | 42.2 |
| Qwen2.5-72B-Instruct | 49.0 | 68.5 | 37.5 | 60.5 | 53.9 |
| Qwen3-8B | 61.8 | 69.4 | 51.6 | 42.9 | 56.4 |
| Qwen3-32B | 70.3 | 69.5 | 54.6 | 52.8 | 61.8 |
| Qwen3-235B | 73.7 | 73.1 | 53.9 | 50.0 | 62.7 |
| GPT-4.1-2025-04-14 | 79.5 | 82.9 | 42.0 | 75.0 | 69.8 |
| GPT-4o-2024-08-06 | 68.2 | 78.3 | 34.9 | 54.9 | 59.1 |
| DeepSeek-V3-0324 | 76.6 | 81.2 | 54.7 | 68.5 | 70.3 |
| Verifier Models | |||||
| xVerify-0.5B-I | 78.5 | 86.2 | 42.6 | 72.6 | 70.0 |
| xVerify-8B-I | 78.9 | 85.1 | 42.6 | 74.9 | 70.4 |
| xVerify-9B-C | 77.0 | 81.7 | 48.0 | 69.8 | 69.1 |
| Tencent-Qwen2.5-7B-RLVR | 73.8 | 76.8 | 55.3 | 62.6 | 67.1 |
| CompassVerifier (Qwen3) | |||||
| CompassVerifier-1.7B | 87.1 | 89.4 | 63.0 | 80.2 | 80.0 |
| CompassVerifier-8B | 86.7 | 90.7 | 75.7 | 79.3 | 83.1 |
| CompassVerifier-14B | 90.3 | 91.4 | 79.1 | 82.9 | 85.9 |
| CompassVerifier-32B | 89.6 | 92.3 | 79.8 | 83.0 | 86.2 |
| CompassVerifier (Qwen2.5) | |||||
| CompassVerifier-3B | 85.9 | 87.7 | 71.0 | 77.1 | 80.4 |
| CompassVerifier-7B | 87.7 | 92.6 | 74.8 | 78.5 | 83.4 |
| CompassVerifier-32B | 90.3 | 94.8 | 80.8 | 84.7 | 87.7 |
We also test the performance of CompassVerifier on VerifyBench. To test its robustness to different prompt styles, we evaluate it using both model-specific prompts and the standard prompts from VerifyBench. The results are as follows:
| Model | Model-specific Prompt Acc |
Model-specific Prompt F1 |
VerifyBench Prompt Acc |
VerifyBench Prompt F1 |
|---|---|---|---|---|
| General Models | ||||
| Qwen2.5-7B-Instruct | 65.4 | 39.8 | 60.9 | 45.0 |
| Qwen2.5-32B-Instruct | 78.8 | 58.9 | 72.0 | 55.8 |
| Qwen2.5-72B-Instruct | 78.5 | 61.7 | 63.0 | 50.0 |
| DeepSeek-V3 | 81.8 | 62.2 | 78.6 | 60.9 |
| Verifier Models | ||||
| xVerify-0.5B-I | 77.9 | 66.2 | - | - |
| xVerify-8B-I | 83.2 | 70.7 | - | - |
| xVerify-9B-C | 83.2 | 71.0 | - | - |
| Tencent-Qwen2.5-7B-RLVR | 82.4 | 68.9 | - | - |
| CompassVerifier (Qwen3) | ||||
| CompassVerifier-1.7B | 80.1 | 69.3 | 72.9 | 61.0 |
| CompassVerifier-8B | 84.5 | 72.7 | 79.2 | 55.4 |
| CompassVerifier (Qwen2.5) | ||||
| CompassVerifier-3B | 87.4 | 77.4 | 86.2 | 75.0 |
| CompassVerifier-7B | 88.1 | 79.0 | 86.0 | 73.3 |
| CompassVerifier-32B | 89.7 | 81.1 | 86.8 | 74.3 |
⚠️ Note: When using the VerifyBench Prompt, xVerify and Tencent-Qwen2.5-7B-RLVR will not output the corresponding judgment in the format specified by the instruction, so the scores are "-".
To validate the efficacy of CompassVerifier as a reward model in reinforcement learning (RL), we utilize GRPO to train Qwen3-4B-Base with rule-based verifier Math-Verify, and model-based verifier as the reward model, with Open-S1 as the RL dataset for two epochs. We rigorously evaluate the reasoning capabilities with a metric of the Average@32 rollout score. The results are as follows:
| Model | AIME24 | AIME25 | MATH500 |
|---|---|---|---|
| Original Model Performance | |||
| Qwen3-4B-Base | 2.7 | 1.8 | 34.1 |
| RL with Rule-based Verifier | |||
| Math-Verify | 8.9 | 7.2 | 63.1 |
| RL with Model-based Verifier | |||
| Tencent-RLVR | 17.4 | 16.2 | 80.5 |
| Qwen3-14B | 19.8 | 16.6 | 81.2 |
| Qwen2.5-32B | 19.6 | 15.4 | 81.6 |
| CompassVerifier-7B (Qwen2.5) | 21.2 | 17.3 | 82.2 |
| CompassVerifier-32B (Qwen2.5) | 21.2 | 17.2 | 83.3 |
@article{CompassVerifier,
title={{CompassVerifier: A Unified and Robust Verifier for Large Language Models}},
author={Shudong Liu and Hongwei Liu and Junnan Liu and Linchen Xiao and Songyang Gao and Chengqi Lyu and Yuzhe Gu and Wenwei Zhang and Derek F. Wong and Songyang Zhang and Kai Chen},
year={2025},
}