Extended-Kalman-Filter

This repository contains an implementation of the Extanded Kalman filter for 2D object tracking based on two different types of observations.

Introduction

For a linear state-space model driven by temporally uncorrelated Gaussian noise, R. E. Kalman derived a recursive algorithm that computes the exact optimal minimum mean square estimate of the hidden state s_k at instant k given a sequence of observations z_1:k = {z₁, z₂, . . . , z_k} from instant 1 up to instant k. However, in many real-world scenarios, the assumptions of linearity and Gaussianity may not be realistic. For these nonlinear, non-Gaussian systems, the recursive estimation problem requires the recursive propagation of the full posterior probability distribution of the hidden state conditioned on the observations. Unfortunately, in a general nonlinear, non-Gaussian setting, there is no analytically tractable solution for exact computation of the optimal MMSE estimate. Approximations become therefore necessary.

There are several different approaches to approximate the posterior distribution of the hidden state vector in general nonlinear estimation problems. The most popular of them are numerical and parametric approximations. A good example of parametric approximation is the well-known Extended Kalman Filter introduced by B. D. O. Anderson and J.B. MOORE in 1979. The EKF approximates the posterior probability density function of the hidden state vector at each instant k, p(s_k|z_1:k), by a single multivariate Gaussian function whose mean, s'_k|k, and corresponding covariance matrix, P_k|k are then updated in the instant k + 1 using the standard Kalman filter recursions associated with the linearized state and observation models.

As an alternative to parametric methods like the EKF, numerical methods such as grid filters attempt to represent the continuous state space by discrete, finite lattices. But these grid filters and Sequential Monte Carlo methods are a whole different story/repo.

Dependencies, compilation and running

In order to successfully run this project, the Term 2 Simulator term2_sim should be downloaded. Here is the link to download it for different platforms.

From the tools perspective, the following packages are necessary:

• cmake >= 3.5
• make >= 4.1 (Linux, Mac), 3.81 (Windows)
• gcc/g++ >= 5.4

The filter communicates with simulator via uWebSocketIO.

Clone this repo into your computer, install all dependencies into default folders or update Makefile with your local paths. Compile the program with make command.

Run the ExtendedKF and term2_sim on the same computer. Both applications will connect to each other via port 4567. They will exchange JSON objects containing object trajectory parameters on the simulator side and their estimation on the Extended Kalman filter side.

This program was tested in Mac OS X 10.13.2 / Xcode 9.2 environment, but it should run in Linux as well.

Extended Kalman Filter

Under the hood, the Extended Kalman filetr utilizes first order terms in the Taylor series expansion of the nonlinear state and measurement equations and approximates the posterior pdf of the hidden state conditioned on the observations by a multivariate normal function.

The filter algorithm is initilized with the first measurments. See, FusionEKF::ProcessMeasurement method in the FusionEKF.cpp. In the consecutive timestamps the following steps are executed:

• Prediction step, where we predict a next positon of the object and its covariance matrix. See, KalmanFilter::Predict() and FusionEKF::ProcessMeasurement methods in kalman_filter.cpp and FusionEKF.cpp respectively.
• Update step, where depending on the source of the measurements, we update the tracking object position with a lidar H_Lidar and R_Lidar matrices or H_Jacobian and R_Radar.

Simulation Results

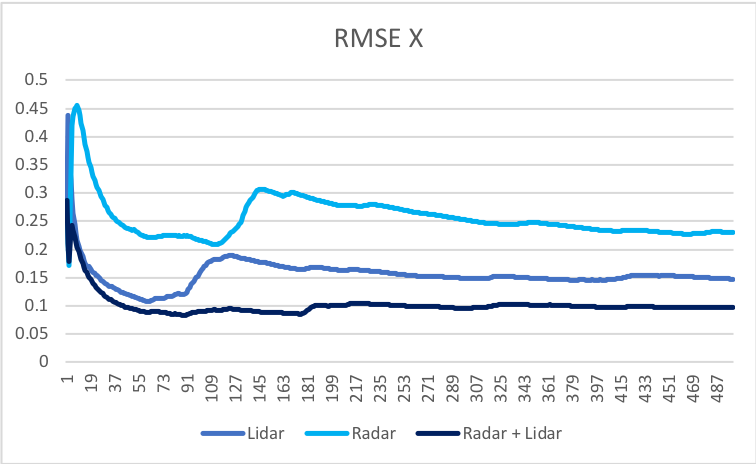
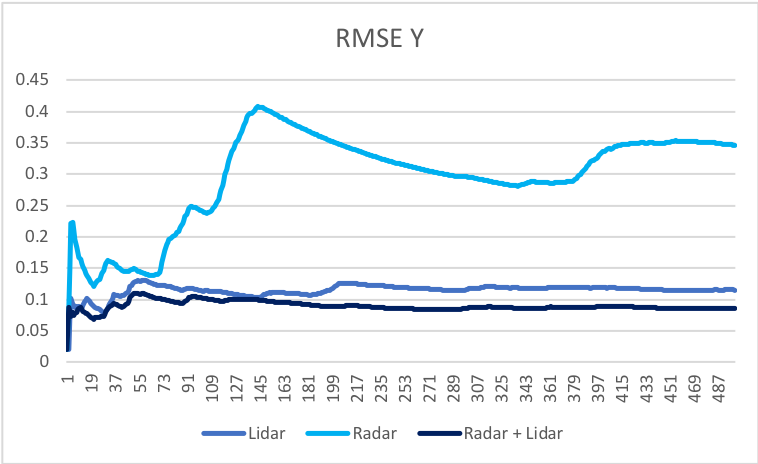
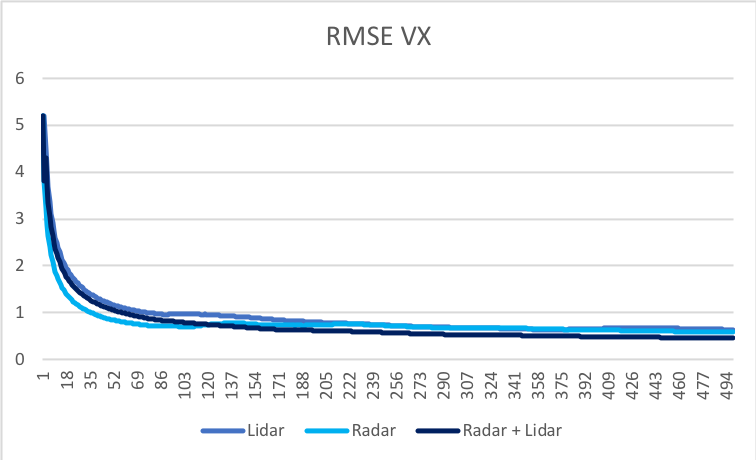
In order to test an EKF trackingapproach a simulation was performed. In that simulation two sensors (lidar and radar) were tracking the object (a blue car) on 2D plane. These results are shown in a figures below.

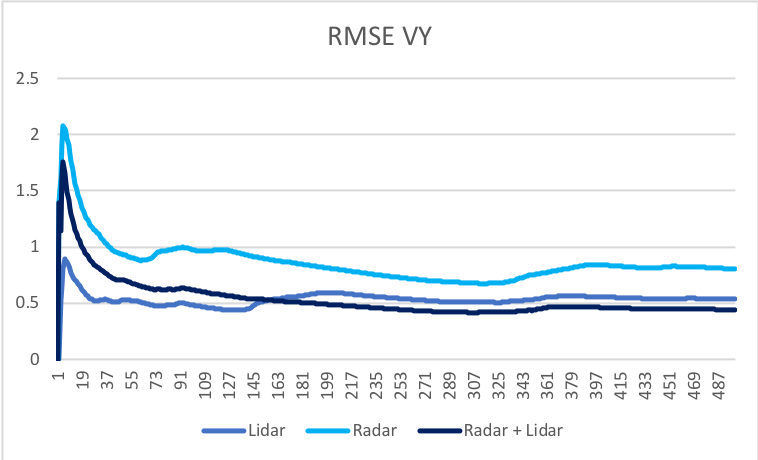For each component of the state vector, the Extanded Kalman filter performs better when provided with both measurments, from a radar and a lidar sensors.

License

Contents of this repository are licensed under MIT License agreement.