-
Notifications
You must be signed in to change notification settings - Fork 14k
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
- Loading branch information
Showing
3 changed files
with
176 additions
and
0 deletions.
There are no files selected for viewing
Binary file not shown.
Loading
Sorry, something went wrong. Reload?
Sorry, we cannot display this file.
Sorry, this file is invalid so it cannot be displayed.
176 changes: 176 additions & 0 deletions
176
0142-Linked-List-Cycle-ii/Article/0142-Linked-List-Cycle-ii.md
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,176 @@ | ||
| # LeetCode 第 142 号问题:环形链表 II | ||
|
|
||
| > 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。 | ||
| > | ||
| > 同步博客:https://www.algomooc.com | ||
|
|
||
| 今天分享的题目来源于 LeetCode 上第 142 号问题:环形链表II。题目难度为 Medium 。 | ||
|
|
||
| ### 题目描述 | ||
|
|
||
| 给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 `null`。 | ||
|
|
||
| 为了表示给定链表中的环,我们使用整数 `pos` 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 `pos` 是 `-1`,则在该链表中没有环。 | ||
|
|
||
| **示例 1:** | ||
|
|
||
| ``` | ||
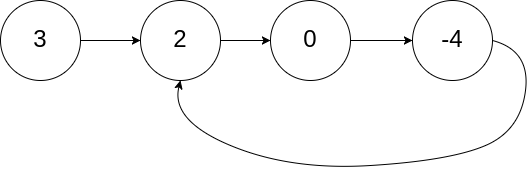
| 输入:head = [3,2,0,-4], pos = 1 | ||
| 输出:tail connects to node index 1 | ||
| 解释:链表中有一个环,其尾部连接到第二个节点。 | ||
| ``` | ||
|
|
||
|  | ||
|
|
||
| **示例 2:** | ||
|
|
||
| ``` | ||
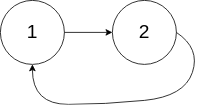
| 输入:head = [1,2], pos = 0 | ||
| 输出:tail connects to node index 0 | ||
| 解释:链表中有一个环,其尾部连接到第一个节点。 | ||
| ``` | ||
|
|
||
|  | ||
|
|
||
| **示例 3:** | ||
|
|
||
| ``` | ||
| 输入:head = [1], pos = -1 | ||
| 输出:no cycle | ||
| 解释:链表中没有环。 | ||
| ``` | ||
|
|
||
|  | ||
|
|
||
| **进阶:** | ||
|
|
||
| 你是否可以不用额外空间解决此题? | ||
|
|
||
| ### 题目解析 - 哈希表 | ||
|
|
||
| 普通解法就是利用哈希表保存访问过的节点, 同时遍历过程中检查哈希表中是否已存在相同的节点 | ||
|
|
||
| ### 代码实现 | ||
|
|
||
| ```javascript | ||
| /** | ||
| * JavaScript 描述 | ||
| * 哈希表方法 | ||
| */ | ||
| var detectCycle = function(head) { | ||
| let res = [ ]; | ||
| while (head !== null) { | ||
| if (res.includes(head)) { | ||
| return head; | ||
| } | ||
| res.push(head); | ||
| head = head.next; | ||
| } | ||
| return null; | ||
| }; | ||
| ``` | ||
|
|
||
| ### 复杂度分析 | ||
|
|
||
| - 时间复杂度:**O(n)** | ||
| - 空间复杂度:**O(n)** | ||
|
|
||
| ### 题目解析 - Floyd 算法 | ||
|
|
||
| Floyd算法 可以达到常量空间解决此问题. | ||
|
|
||
| 我在维基百科找到了这个算法描述, 在此引用一下. | ||
|
|
||
| **Floyd判圈算法**(**Floyd Cycle Detection Algorithm**),又称 **龟兔赛跑算法**(**Tortoise and Hare Algorithm**),是一个可以在[有限状态机](https://zh.wikipedia.org/wiki/有限状态机)、[迭代函数](https://zh.wikipedia.org/wiki/迭代函数)或者[链表](https://zh.wikipedia.org/wiki/链表)上判断是否存在[环](https://zh.wikipedia.org/wiki/環_(圖論)),求出该环的起点与长度的算法。 | ||
|
|
||
| 如果有限状态机、迭代函数或者链表存在环,那么一定存在一个起点可以到达某个环的某处 ( 这个起点也可以在某个环上 )。 | ||
|
|
||
| 初始状态下,假设已知某个起点节点为节点 *S*。现设两个指针 `t` 和 `h` ,将它们均指向 *S*。 | ||
|
|
||
| 接着,同时让 `t` 和 `h` 往前推进,但是二者的速度不同:`t` 每前进 `1` 步, `h` 前进 `2` 步。只要二者都可以前进而且没有相遇,就如此保持二者的推进。当 `h` 无法前进,即到达某个没有后继的节点时,就可以确定从 *S* 出发不会遇到环。反之当 `t` 与 `h` 再次相遇时,就可以确定从 S 出发一定会进入某个环,设其为环 *C*。 | ||
|
|
||
| 如果确定了存在某个环,就可以求此环的起点与长度。 | ||
|
|
||
| 上述算法刚判断出存在环 *C* 时,显然 t 和 `h` 位于同一节点,设其为节点 *M*。显然,仅需令 `h` 不动,而t不断推进,最终又会返回节点 *M*,统计这一次t推进的步数,显然这就是环 *C* 的长度。 | ||
|
|
||
| 为了求出环 *C* 的起点,只要令h仍均位于节点 *M* ,而令t返回起点节点 *S* ,此时h与t之间距为环 *C* 长度的整数倍。随后,同时让 `t` 和 `h` 往前推进,且保持二者的速度相同:`t` 每前进 `1` 步,`h` 前进 `1` 步。持续该过程直至 `t` 与 `h` 再一次相遇,设此次相遇时位于同一节点 *P*,则节点 *P* 即为从节点 *S* 出发所到达的环 *C* 的第一个节点,即环 *C* 的一个起点。 | ||
|
|
||
| **看完之后是不是很多疑点, 觉得为什么会这样呢?** | ||
|
|
||
| 下面用数学简单证明一下 | ||
|
|
||
| 假设 链表的节点数为 `num`, 从 head 到链表环入口节点数为 `m` (不包含入口节点), 环的节点数为 `n`, 链表环入口设点为 *P* | ||
|
|
||
| 由此可得 `num = m + n` | ||
|
|
||
| 假设 慢指针 `Tortoise` (乌龟) 每次走 `1` 个节点, 走了 `x` 步 | ||
|
|
||
| 假设 快指针 `Hare` (兔子) 每次走 `2` 个节点, 走了 `f` 步 | ||
|
|
||
| 那么 `f = 2x` | ||
|
|
||
| 当第一次相遇时, 必然是在环内, 设其点为 *M*, 兔子第一次到达 *M* 点后至少又在环内饶了一圈后追上乌龟, | ||
|
|
||
| 假设绕了 `k` 圈, 那么可以得到 | ||
|
|
||
| `f = x + kn` | ||
|
|
||
| 兔子到达 *P* 点的步数为 | ||
|
|
||
| `f = m + kn` | ||
|
|
||
| 由 `f = 2x` 和 `f = x + kn` 两个等式可以得到 `x = kn` | ||
|
|
||
| 由 `f = m + kn` 和 `x = kn` 可知, 乌龟到达 *P* 点还需要走 `m` 步 | ||
|
|
||
| 而 `m` 的长度正是从 head 到链表环入口节点数的长度, 这是未知的, | ||
|
|
||
| 那么让兔子从 head 以乌龟的速度走, 乌龟在 *M* 点走, 当兔子和乌龟相遇时即走了 `m` 步, 也就到达了 *P* 节点. | ||
|
|
||
| ### 动画描述 | ||
|
|
||
|  | ||
|
|
||
| ### 代码实现 | ||
|
|
||
| ```java | ||
| /** | ||
| * JavaScript 描述 | ||
| * Floyd判圈算法 | ||
| */ | ||
| var detectCycle = function(head) { | ||
| if (head == null) { | ||
| return head; | ||
| } | ||
| // 设置快慢指针 | ||
| let tortoise = head, | ||
| hare = head; | ||
| // 检查链表是否有环 | ||
| while (true) { | ||
| if (hare == null || hare.next == null) { | ||
| return null; | ||
| } | ||
| hare = hare.next.next; | ||
| tortoise = tortoise.next; | ||
| if (hare == tortoise) { | ||
| break; | ||
| } | ||
| } | ||
| // 兔子和乌龟第二次相遇找到环入口 | ||
| hare = head; | ||
| while (hare != tortoise) { | ||
| hare = hare.next; | ||
| tortoise = tortoise.next; | ||
| } | ||
| return hare; | ||
| }; | ||
| ``` | ||
|
|
||
| ### 复杂度分析 | ||
|
|
||
| - 时间复杂度:**O(n)** | ||
| - 有环情况下, 第一次和第二次相遇, 乌龟步数都小于链表节点数, 因此与链表节点数成线性关系; | ||
| - 无环情况下, 兔子大约需要 n/2 步数到达最后, 因此也与链表节点数成线性关系. | ||
| - 空间复杂度:**O(1)** , 双指针使用常数大小的额外空间 | ||
|
|
||
|  |