TLR: Time-Lagged Recurrence ($\alpha_\eta$)

Python code and Jupyter notebooks support the manuscript "Revisiting the Predictability of Dynamical Systems: A New Local Data-Driven Approach," which introduces the Time-Lagged Recurrence (TLR) as a novel predictability index.

Introduction

Nonlinear dynamical systems are ubiquitous in nature and they are hard to forecast. Not only they may be sensitive to small perturbations in their initial conditions, but they are often composed of processes acting at multiple scales. Classical approaches based on the Lyapunov spectrum rely on the knowledge of the dynamic forward operator, or of a data-derived approximation of it. This operator is typically unknown, or the data are too noisy to derive a faithful representation. Here, we propose a new data-driven approach to analyze the local predictability of dynamical systems. This method, based on the concept of recurrence, is closely linked to the well-established framework of local dynamical indices. Applied to both idealized systems and real-world datasets, this new index shows results consistent with existing knowledge, proving its effectiveness in estimating local predictability. Additionally, we discuss its relationship with local dynamical indices, illustrating how it complements the previous framework as a more direct measure of predictability. Furthermore, we explore its reflection of the scale-dependent nature of predictability, its extension that includes a weighting strategy, and its real-time application. We believe these aspects collectively demonstrate its potential as a powerful diagnostic tool for complex systems.

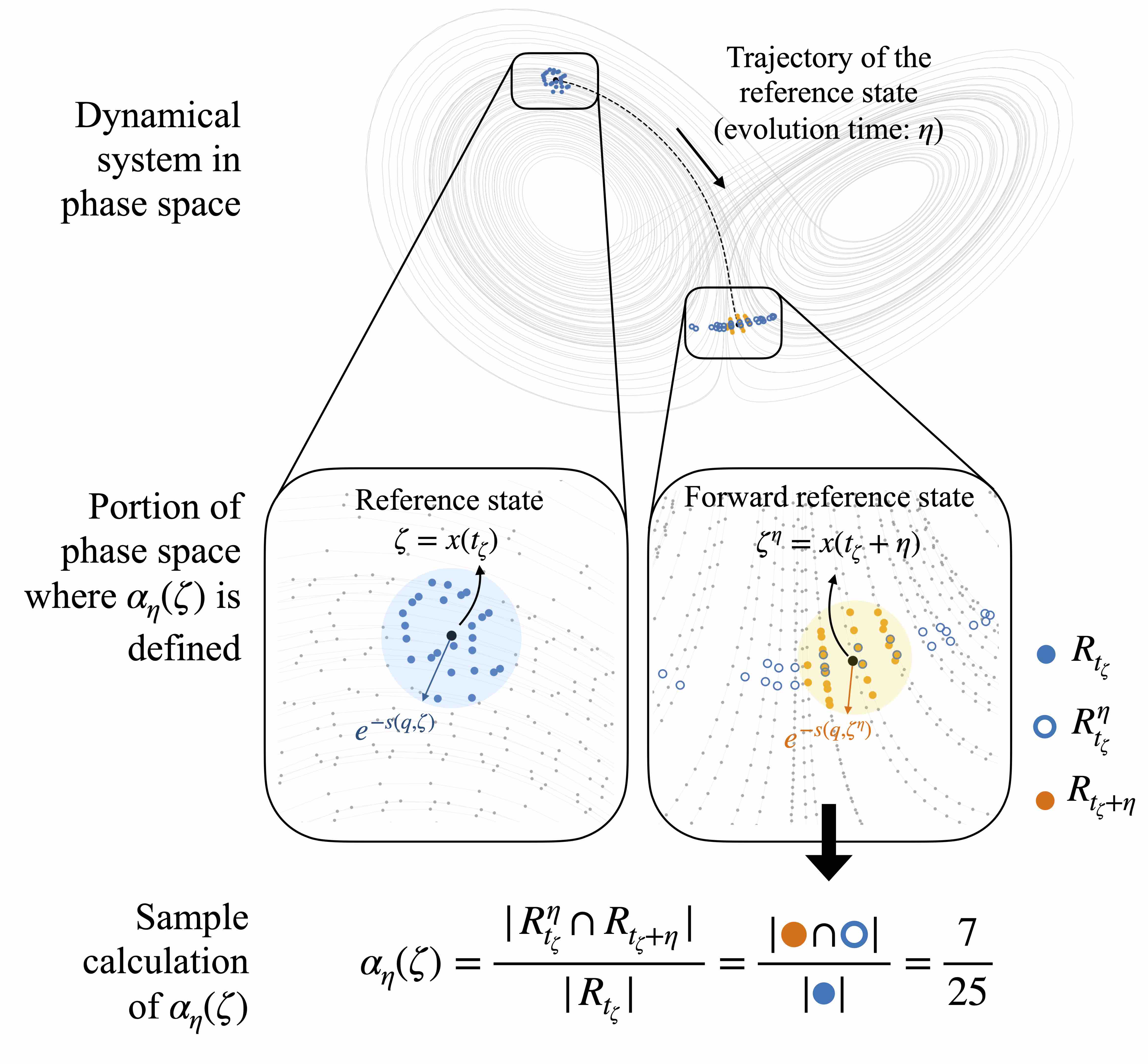
Schematic illustration of our index. For further details, please refer to the manuscript.

Content

Scripts

Functions for computing TLR ($\alpha_\eta$), along with the other two local dynamical indices: local dimension $d$ and persistence $\Theta$.

• local_indices.py

Functions for postprocessing and visualization.

• postprocessing.py

Example

Driver file for computing TLR ($\alpha_\eta$), using the Lorenz-63 system as an example.

• driver_sh.sh

Driver file for reproducing Figure 2 in the main text of the manuscript.

• driver_sh_plotting.sh

Data

All data used in this paper are available. Datasets from Brunton et al. (2017) [1] are in folder datasets, while the Julia scripts for generating others are in folder julia_code. The ERA5 reanalysis data used in this study are available at ERA5.

[1] Brunton, Steven L., et al. "Chaos as an intermittently forced linear system." Nature communications 8.1 (2017): 19.