Source code for http://arxiv.org/abs/1504.01344
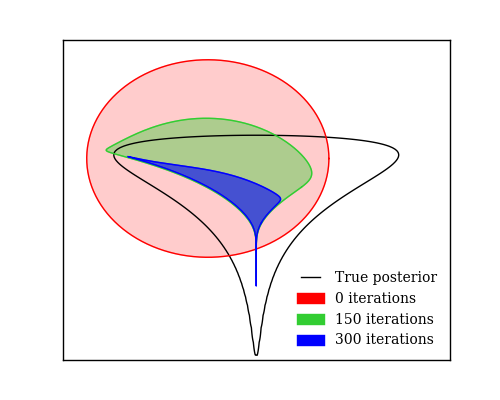
We show that unconverged stochastic gradient descent can be interpreted as a procedure that samples from a nonparametric variational approximate posterior distribution. This distribution is implicitly defined as the transformation of an initial distribution by a sequence of optimization updates. By tracking the change in entropy over this sequence of transformations during optimization, we form a scalable, unbiased estimate of the variational lower bound on the log marginal likelihood. We can use this bound to optimize hyperparameters instead of using cross-validation. This Bayesian interpretation of SGD suggests improved, overfitting-resistant optimization procedures, and gives a theoretical foundation for popular tricks such as early stopping and ensembling. We investigate the properties of this marginal likelihood estimator on neural network models.
Authors: Dougal Maclaurin, David Duvenaud, and Ryan P. Adams
Feel free to email us with any questions at ([email protected]), ([email protected]).
For a look at some directions that didn't pan out, take a look at our early research log. We also played around with tracking the entropy of Hamiltonian Monte Carlo without accept/reject steps, but that didn't make it into the final version of the paper.