Skip to content

Latest commit

 

History

History
122 lines (84 loc) · 3.54 KB

README.md

File metadata and controls

122 lines (84 loc) · 3.54 KB
Raw

Rain Terraces (Trapping Rain Water) Problem

Given an array of non-negative integers representing terraces in an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

Rain Terraces

Examples

Example #1

Input: arr[] = [2, 0, 2]
Output: 2
Structure is like below:

| |
|_|

We can trap 2 units of water in the middle gap.

Example #2

Input: arr[] = [3, 0, 0, 2, 0, 4]
Output: 10
Structure is like below:

     |
|    |
|  | |
|__|_| 

We can trap "3*2 units" of water between 3 an 2,
"1 unit" on top of bar 2 and "3 units" between 2 
and 4. See below diagram also.

Example #3

Input: arr[] = [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]
Output: 6
Structure is like below:

       | 
   |   || |
_|_||_||||||

Trap "1 unit" between first 1 and 2, "4 units" between
first 2 and 3 and "1 unit" between second last 1 and last 2.

The Algorithm

An element of array can store water if there are higher bars on left and right. We can find amount of water to be stored in every element by finding the heights of bars on left and right sides. The idea is to compute amount of water that can be stored in every element of array. For example, consider the array [3, 0, 0, 2, 0, 4], We can trap "3*2 units" of water between 3 an 2, "1 unit" on top of bar 2 and "3 units" between 2 and 4. See below diagram also.

Approach 1: Brute force

Intuition

For each element in the array, we find the maximum level of water it can trap after the rain, which is equal to the minimum of maximum height of bars on both the sides minus its own height.

Steps

  • Initialize answer = 0
  • Iterate the array from left to right:
    • Initialize max_left = 0 and max_right = 0
    • Iterate from the current element to the beginning of array updating: max_left = max(max_left, height[j])
    • Iterate from the current element to the end of array updating: max_right = max(max_right, height[j])
    • Add min(max_left, max_right) − height[i] to answer

Complexity Analysis

Time complexity: O(n^2). For each element of array, we iterate the left and right parts.

Auxiliary space complexity: O(1) extra space.

Approach 2: Dynamic Programming

Intuition

In brute force, we iterate over the left and right parts again and again just to find the highest bar size up to that index. But, this could be stored. Voila, dynamic programming.

So we may pre-compute highest bar on left and right of every bar in O(n) time. Then use these pre-computed values to find the amount of water in every array element.

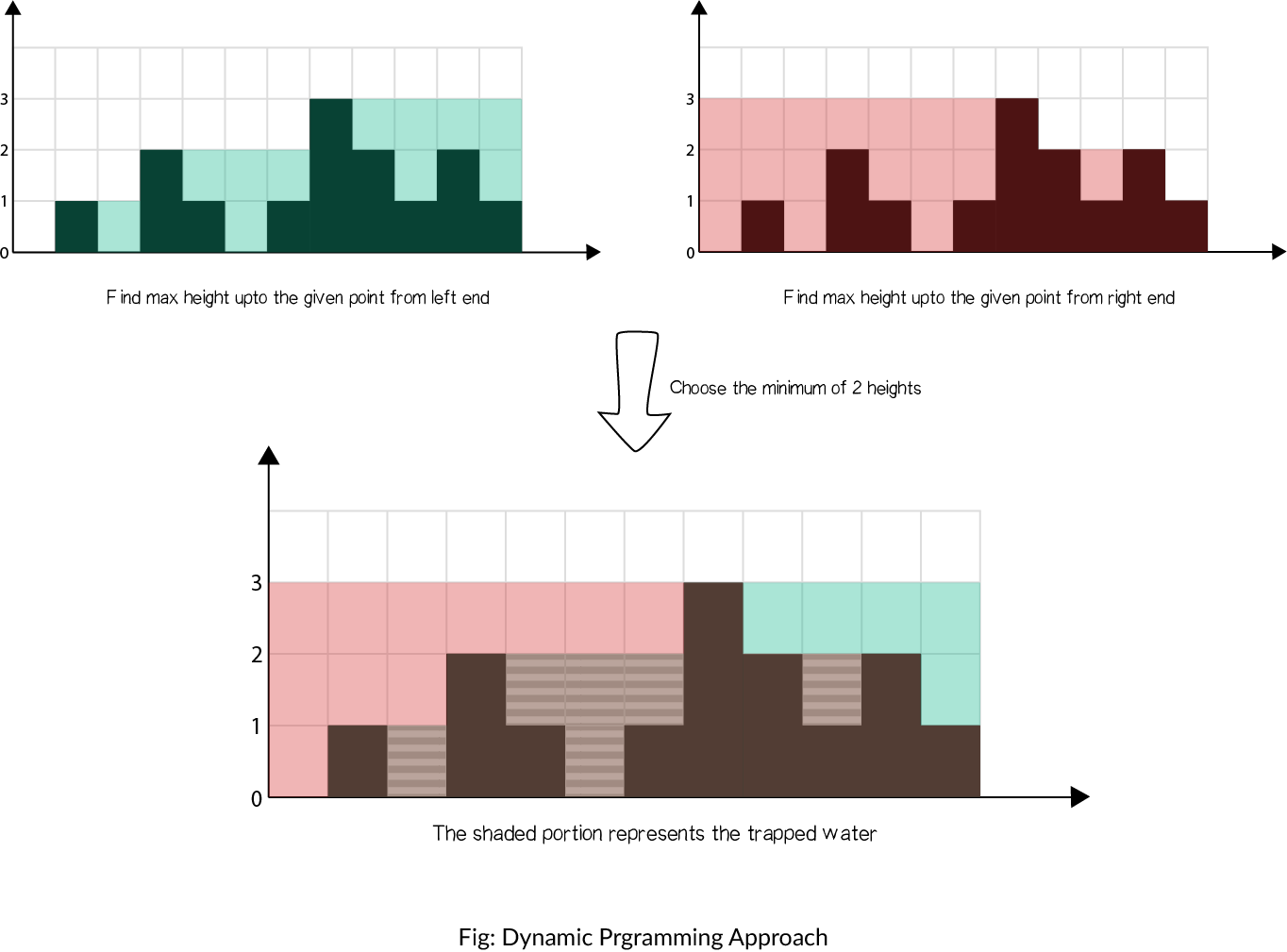
The concept is illustrated as shown:

DP Trapping Rain Water

Steps

  • Find maximum height of bar from the left end up to an index i in the array left_max.
  • Find maximum height of bar from the right end up to an index i in the array right_max.
  • Iterate over the height array and update answer:
    • Add min(max_left[i], max_right[i]) − height[i] to answer.

Complexity Analysis

Time complexity: O(n). We store the maximum heights upto a point using 2 iterations of O(n) each. We finally update answer using the stored values in O(n).

Auxiliary space complexity: O(n) extra space. Additional space for left_max and right_max arrays than in Approach 1.

References