-
Notifications
You must be signed in to change notification settings - Fork 18
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Matrix valued coefficients as input to Wilson #105
Comments
|
Except for a small typo, I think your example should do the correct thing. However, if you want to use redundant arrays as input, you might want to check that they have been actually properly symmetrized. E.g. one could use a function like from wilson.util import smeftutil
def C_arrays_to_C_wcxf(C_arrays):
C_wcxf = smeftutil.arrays2wcxf_nonred(smeftutil.add_missing(C_arrays))
C_arr_sym = smeftutil.wcxf2arrays_symmetrized(C_wcxf)
for k,v in C_arrays.items():
if not np.all(C_arr_sym[k] == v):
raise ValueError(f'Input array "{k}" is not properly symmetrized.')
return C_wcxfWe could think about including such a function in a Another idea would be to check whether the input dictionary contains keys for redundant arrays (i.e. |
|
Thanks Peter! For the code, my quick opinion is that a |
|
I agree that correct symmetrization must definitely be checked when allowing non-redundant input. Even if correct matching should give you the correctly symmetrized WCs, it's something to easily get wrong and it would lead to weird and hard to debug errors. I advise against switching between assuming redundant and non-redundant conventions based on user input. This is prone to lead to unintended behaviour, e.g. in the case of typos. It is much better IMO to have to separate options and fail in both cases if the assumptions are not met. |
|
An update from real world testing - the |
|
Spoke a little too soon, sometimes I get differences that are relatively big, but absolutely small, e.g. |
|
I'm a bit surprised that you get such big relative differences when going to the non-redundant description and then back to the symmetrized one. Do you get this only in cases where the value is actually zero up to numerical uncertainties? Can you maybe provide an example for which you get such results? |
|
No, the example I found was for a non-zero WC (albeit very small, as it suppressed by a bunch of CKM factors and the charm mass). Here's a simplified version of my code from math import pi
import numpy as np
from wilson.util import smeftutil
from ckmutil.ckm import ckm_tree
xi = np.array((-0.8, 0, 0))
_Vus = 0.2253
_Vub = 0.0041
_Vcb = 0.0421
_delta = 1.14
vckm1 = ckm_tree(_Vus, _Vub, _Vcb, _delta)
vckm2 = np.array(
((0.974281, 0.2253, 0.00171214 - 0.0037254j),
(-0.225172 - 0.000152808j, 0.973409 - 0.0000353365j, 0.0421),
(0.00781865 - 0.0036264j, -0.0414033 - 0.000838595j, 0.99910))
)
print(np.allclose(vckm1, vckm2, rtol=1e-6))
print(vckm1 / vckm2 - 1)
vckm = vckm2
yudiag = np.diag((0, 1.3/174, 1))
yu = vckm.T.conj() @ yudiag
yubar = yu.conj()
qu1 = ( 3 * np.einsum("i,j,Al,Ak->ijkl", xi, xi, yu, yubar) / (128)
+1 * np.einsum("A,j,il,Ak->ijkl", xi, xi, yu, yubar) / (192)
+1 * np.einsum("A,i,Al,jk->ijkl", xi, xi, yu, yubar) / (192)
-1 * np.einsum("A,A,il,jk->ijkl", xi, xi, yu, yubar) / (96) )
print(qu1[0,0,2,1])
def C_arrays_to_C_wcxf(C_arrays):
C_wcxf = smeftutil.arrays2wcxf_nonred(smeftutil.add_missing(C_arrays))
C_arr_sym = smeftutil.wcxf2arrays_symmetrized(C_wcxf)
for k,v in C_arrays.items():
# if not np.all(C_arr_sym[k] == v):
if not np.allclose(C_arr_sym[k], v, atol=0):
raise ValueError(f'Input array "{k}" is not properly symmetrized.')
return C_wcxf
try:
C_arrays_to_C_wcxf({"qu1": qu1})
except ValueError as e:
print(e)
C_wcxf = smeftutil.arrays2wcxf_nonred(smeftutil.add_missing({"qu1": qu1}))
C_arr_sym = smeftutil.wcxf2arrays_symmetrized(C_wcxf)
for i in range(3):
for j in range(3):
for k in range(3):
for l in range(3):
if not np.isclose(qu1[i,j,k,l], C_arr_sym["qu1"][i,j,k,l], atol=0):
print((i,j,k,l), qu1[i,j,k,l], C_arr_sym["qu1"][i,j,k,l], qu1[i,j,k,l] / C_arr_sym["qu1"][i,j,k,l])The only "wrong" element is the C_1132, which I print. |
|
Okay, on further investigation, in this particular case, with only a first gen NP coupling (my |
When matching from a UV theory onto the SMEFT, often one gets pretty simple generic formulas for the SMEFT coefficients. As an example, take this from the wilson paper (bottom of page 9)

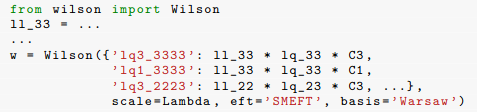
But actually typing out all the coefficients is tedious and error prone. Again from there, you give the example code
If I'm correct, there are actually another 17 coefficients hidden in that "..." that you didn't bother to type out, and of course you have to remember which are the non-redundant ones.
Instead, it's pretty easy to use the following code
to generate all the wilson coefficients (in what should be the basis where coefficients have the same symmetries as the operators).
Then you can do
to get a dictionary with just the non-redundant coefficients needed to initialise a Wilson instance.
My questions are:
arrays2wcxf_nonredis what I want, notarrays2wcxf.and
Wilsoninstance? I would say using the numpy summation makes it much easier to see if you have the correct formula, and much less typo prone.The text was updated successfully, but these errors were encountered: