-
Notifications
You must be signed in to change notification settings - Fork 26
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
MOD issue #91
Comments
|
Oberon has not negative literals. I.e. |
|
Unary minus has lower priority, than MOD. |
|
The corresponding topic on the forums: Приоритет унарного минуса Повысить приоритет унарного минуса (и плюса) легко! Но стОит ли... |
|
hello, @Oleg-N-Cher! also, this is from the report: My understanding, based on communication with ETH team is that Wirth himself and ETH compilers always assume that the remainder cannot be negative, just like we learnt in school. Back then I tested many compilers and I believe only ooc wasn't following the report on it. All ETH compilers have checks for this, and all Wirth's compilers handle this issue. @dcwbrown would you run builds or take a look at the pull request #92 to confirm it's ok to merge? |
|
Well, this is quite interesting. The specs from the original Oberon, Oberon 2 and Oberon 07+ all define DIV and MOD behaviour only for positive divisors. Here they are: From Oberon (Wirth October 1990) From Oberon2 (H. Mössenböck, N. Wirth) From Oberon 2007+ (Wirth May 2016) Note that Wirth has moved his description from prose to formula in his latest spec, but that he still limits the spec to describing cases where 0 <= r < y. Now consider the cases where x is negative and y is positive (i.e. where the spec tells us what the correct result must be). The Oberon2 spec actually includes examples: Happily, voc gets these right. (Norayr, you didn't say explicitly whether you acknowledged Olegs point about unary operators, so with apologies for being tedious, to avoid ambiguity: providing you test with (-5) MOD 3 as is required by the Oberon priority rules, you will get the correct (i.e. positive) answer. And so we come to what should happen if the divisor is negative. To be clear, Wirth has chosen explicitly to omit this case from the specification of Oberon. However Component Pascal does define it: They have specified that when the divisor is negative, so is the result of MOD. One can look at it like this: x MOD 5 means: give me an offset in the range 0 .. 4 inclusive. while x MOD (-5) means: give me an offset in the range 0..-4 inclusive. And indeed VOC already conforms to this specification. Therefore VOC conforms accurately to both Wirth's specification, and to the Component Pascal specification. Should we change the existing code? I see these two arguments against making this change.
So, I'm sorry to be in conflict Noray, but I would recommend against making this change. All the best -- Dave. |
|
I think I was not clear, so:
means that I agree with the current situation with operator precedence, and I did not realize in the beginning that my test wasn't revealing anything wrong, and everything regarding that is ok. Thank you, @dcwbrown for explanations. I saw the code handles several cases, but did not understand the reasoning. Now that I know this, and CP solution, it looks reasonable. However it is still unclear to me if that is the best solution of case with negative divisors. RISC Oberon V5 (disk image from 2019-01-21, pdewacht's emulator) traps when divisor is negative in both DIV and MOD operations.
x86 OP2 compiler from Linux ETH Oberon output is interesting. It gives us positive result in case of negative divisor ETH Oberon compiler for ARM. This is compiler from OLR, descendent from the Ceres version. Interesting, that the changelog states: So may be Peter Matthias knows something which is not clear to us? btw, DIV results are also different in three cases: It seems that when 5 DIV -3, it is a rounding issue, and -5 DIV -3 - again, the x86 OP2 bug? But let us come to that later. For now, I am getting back to MOD cases. I hope all the screenshots are correctly loaded. |
|
and I am unable to run new OLR for ARM, which is PO version ported to ARM by Peter, because it crashes parsing one of the home directory files, and I cannot debug and fix it because I have no working PO for ARM. But I understand most likely Peter made it the same way he made S3 OLR for ARM, just like I did in this commit. |
|
regarding the point of backward compatibility and breaking the existing code: |
|
it is good to test how V4 handles this. for now I cannot run any V4, linux versions require very old systems, and I have no windows. |
|
it is interesting that Oberon reports state |
|
ah, because if r is >= 0, then it cannot be at the same time < y which is negative. |
|
this can be found on ulm's compiler site, on a page about differences: http://www.mathematik.uni-ulm.de/oberon/reports/ulmdiff-1994.html
apparently first two Oberon reports were defining DIV and MOD for negative operands on the right side, and the result had to be negative. |
|
May I suggest to have a look at: |
|
today i was reading Josef Templ's Dr. Dobb's Journal Oberon article, published in 1994. In the section 'type constructors' he writes:
|
|
I was reading this paper today and stumbled upon these lines:
One can only guess what this |
|
"more mathematical" means: if b > 0, then 0 <= a MOD b < b |
|
If we look at a common sitution where we Inc modulo and sometimes Dec modulo: FigNr := (FigNr + 1) MOD N; We want |
|
FWIW, I'd have written this as (see change in 4th line),
FigNr := (FigNr + 1) MOD N;
possible := CheckDisplay(FigNr);
IF possible THEN DrawFigure(FigNr)
ELSE FigNr := (FigNr + N - 1) MOD N (* Notice the +N in there *)
END
to avoid any concern about know exactly what MOD does.
Stefan
…On Sun, 13 Sep 2020 08:13:10 -0700 Markow Eduard ***@***.***> wrote:
If we look at a common sitution where we Inc modulo and sometimes Dec
modulo:
FigNr := (FigNr + 1) MOD N;
possible := CheckDisplay(FigNr);
IF possible THEN DrawFigure(FigNr)
ELSE FigNr := (FigNr - 1) MOD N
END
We want
FigNr (before) = FigNr (after Dec) [Modulo N], i.e.
FigNr (before) MOD N = FigNr (after Dec) MOD N.
--
You are receiving this because you are subscribed to this thread.
Reply to this email directly or view it on GitHub:
#91 (comment)
--
Stefan Vorkoetter
http://www.stefanv.com
|
|
Dear Stefan Thanks a lot for your contribution. This is a very good trick if one wants to program in a manner to reuse the statements in different contexts e.g. in Pascal, Modula-2 and Oberon. In our case however we are aiming at a clean solution for implementing the language by means of a compiler. By clearly stating the behaviour of the implementation or even better by generally coming to a conclusion what the correct interpretation for the language Oberon is we offer the programmer the possibility to write the most efficient statements. Eduard |

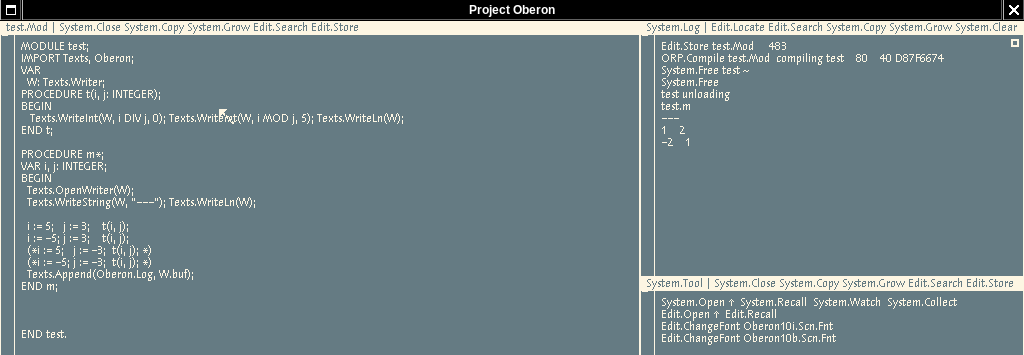
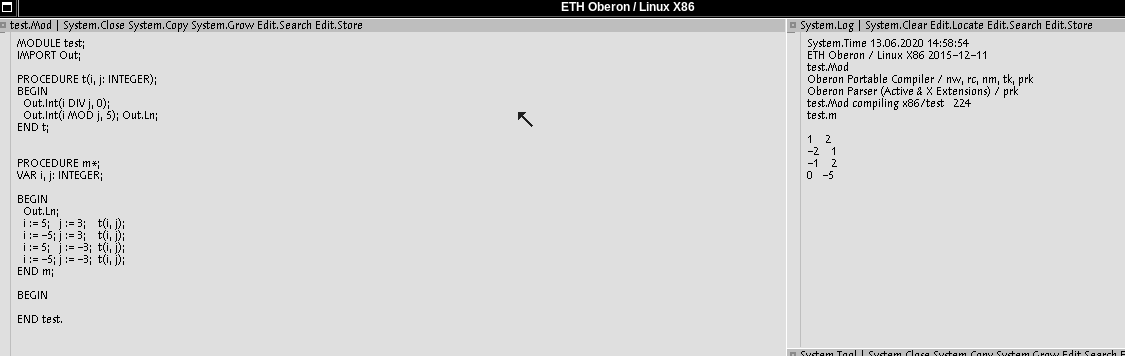
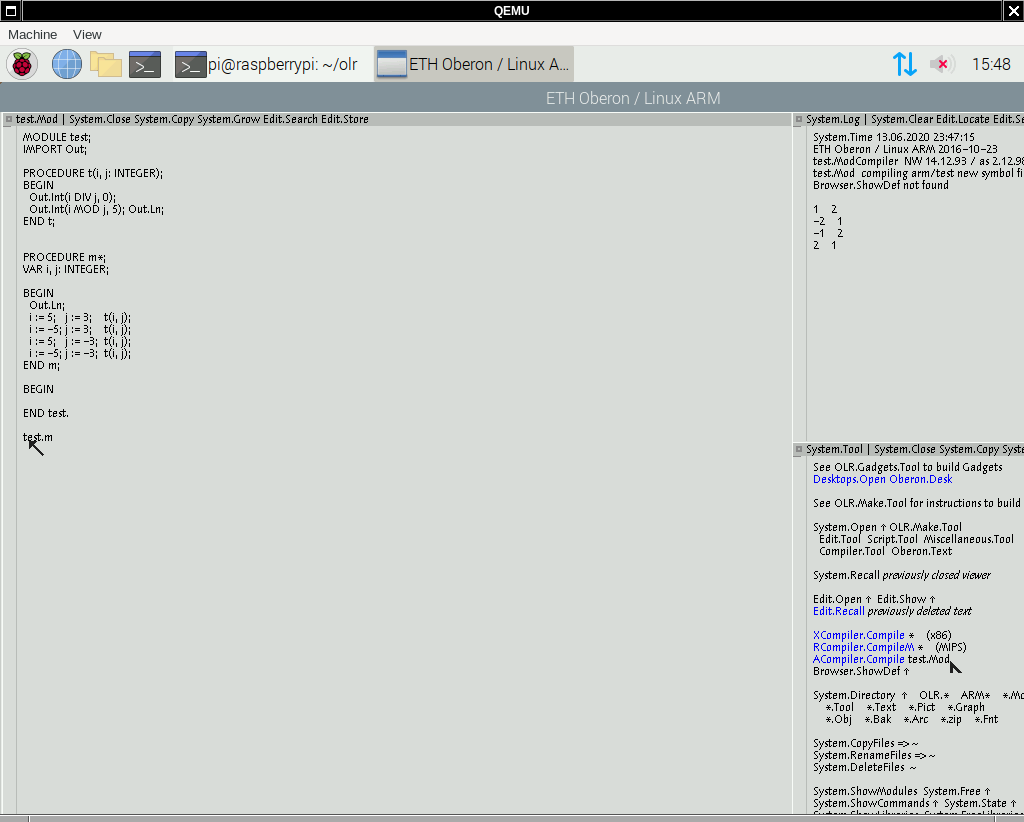

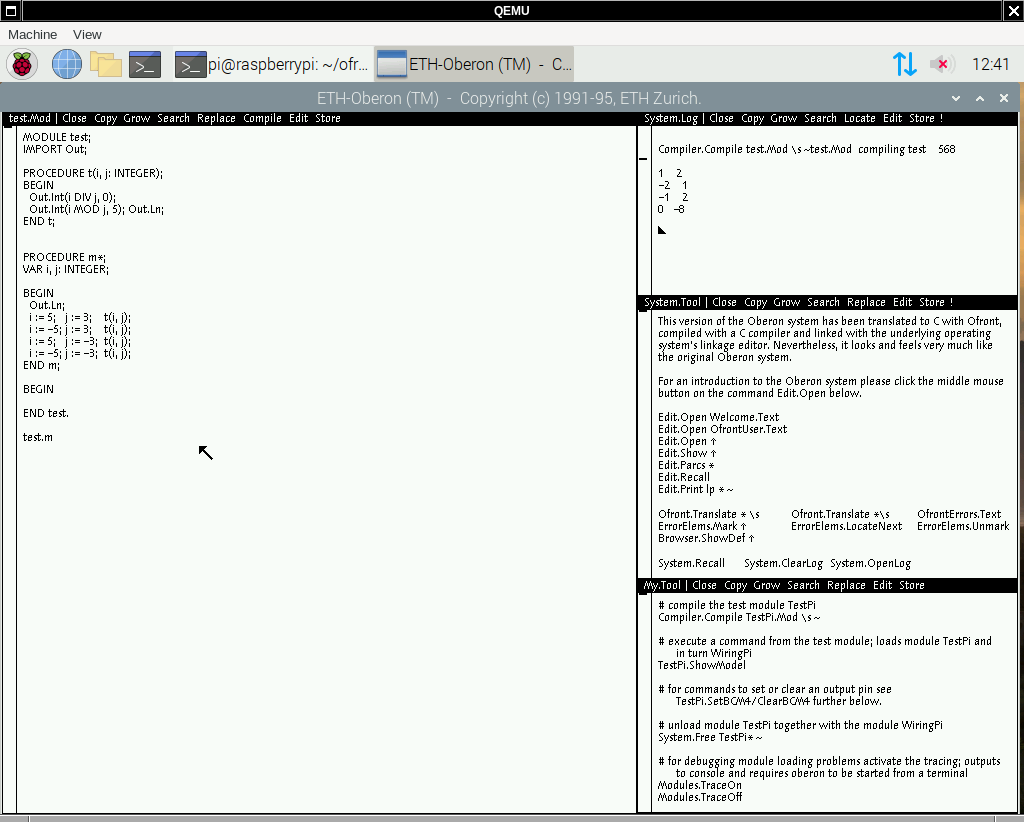

we get -2, as other languages.
should be, according to report: 1.
dealing with it.
The text was updated successfully, but these errors were encountered: