-
Notifications
You must be signed in to change notification settings - Fork 42
Problem Setup
In setting up a phase-field simulation, it is important to understand the role of spatial dimensions in the physics governing the problem, and how that might impact the simulation results and its interpretation. This is particularly important if simulations are being performed in reduced dimensions compared to the actual dimension of the problem, which is a common practice employed to reduce the computational costs.
It is likely that the physical behavior of a certain phenomenon might scale differently in 1D, 2D and 3D. This could be related to the physical processes in the bulk regions of the system or at the interfacial regions or both. For instance, the amount of interfacial region relative to the bulk phase region differs in 1D, 2D and 3D, and also governs many physical aspects of material behavior.
Therefore, it is important to determine how reduced dimensionality might affect predictions or comparison of simulation results with reality. In certain situations, on the other hand, it might be appropriate to setup the problem in reduced dimensions of 1D or 2D due to the inherent symmetry or directionality in the problem. Moreover, for simple microstructure geometries, it might be possible to setup the model in cylindrical or spherical coordinates, which can allow the simplicity of 1D computations while also capturing 2D and 3D behavior of the model accurately.
To demonstrate a case where simulation outcomes can significantly differ in different dimensions, we consider the single seed case of the homogeneous nucleation benchmark problem. A simple phase-field model with a single non-conserved order parameter describes an isothermal pure substance with one liquid phase (order parameter =
We consider a seed nucleus of
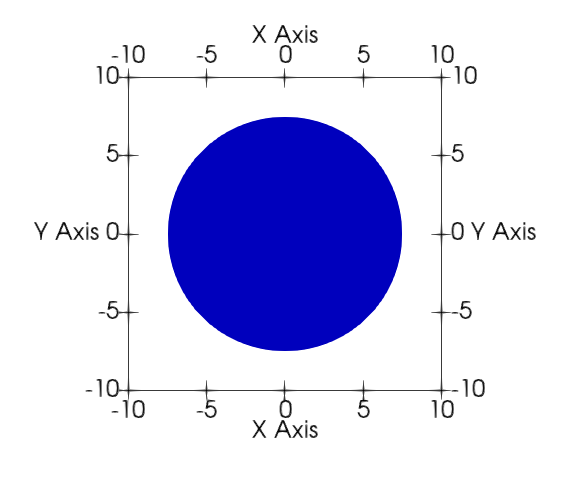
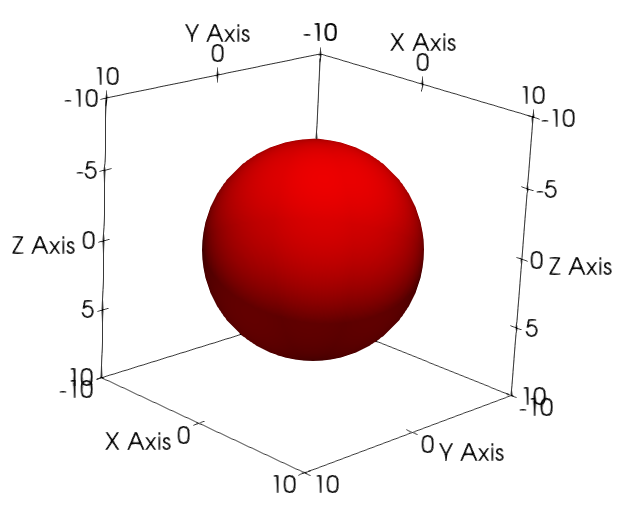
The time evolution of the order parameter, given by the Allen-Cahn equation, was solved using the MOOSE framework. Details of the numerical method can be found in Wu et al. (2021).
The simulations results of nucleus evolution are shown in the figures below: (left) order parameter profile measured radially from the center of domain at different evolution times; (right) radius as a function of evolution time. We see that the seed of same starting radius
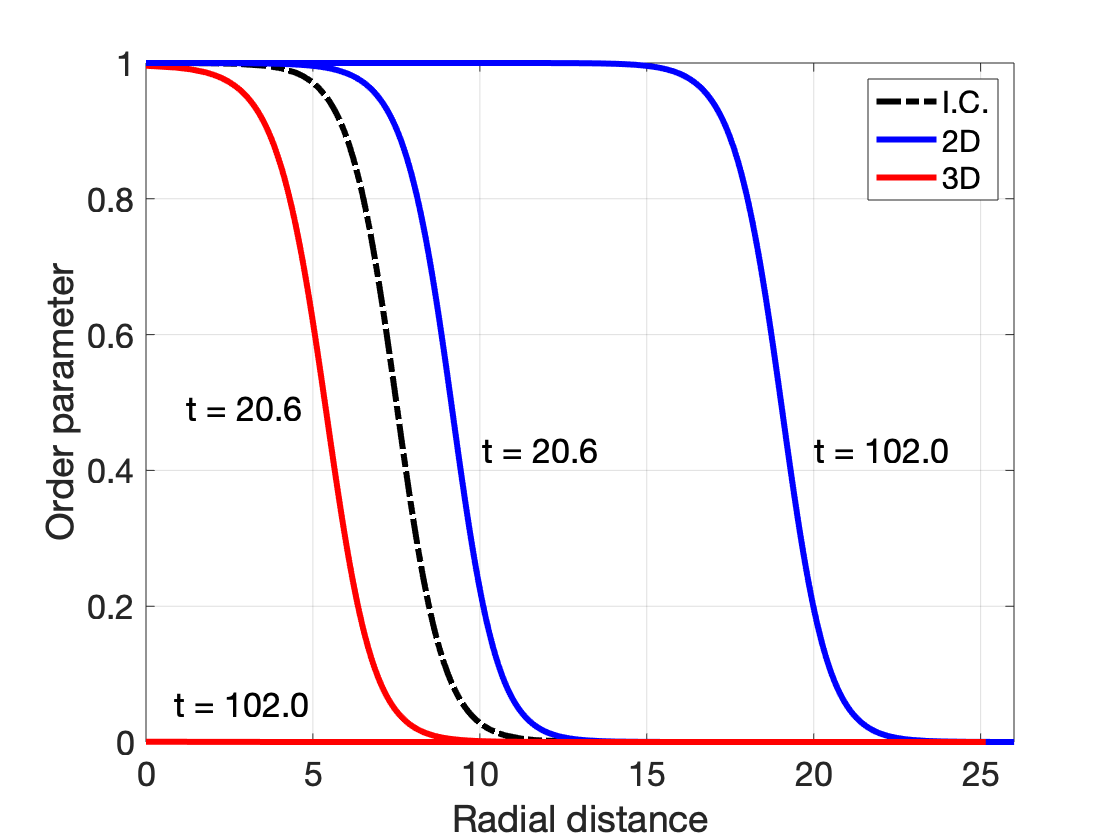
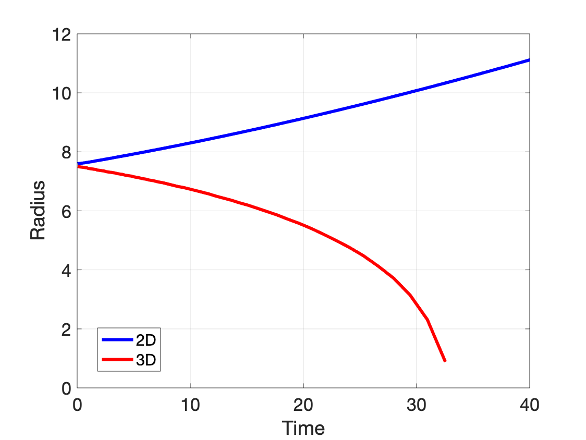
The role of dimensionality in homogeneous nucleation can be understood from the classical nucleation theory where the solid-liquid interface is modeled as a mathematically sharp interface. The interface is a 1D line in a 2D system and a 2D plane in a 3D system. The free energy of the nucleus particle
We can now apply the above sharp-interface analysis to our diffuse interface approximation in the phase-field model. For the given model parameters, we obtain
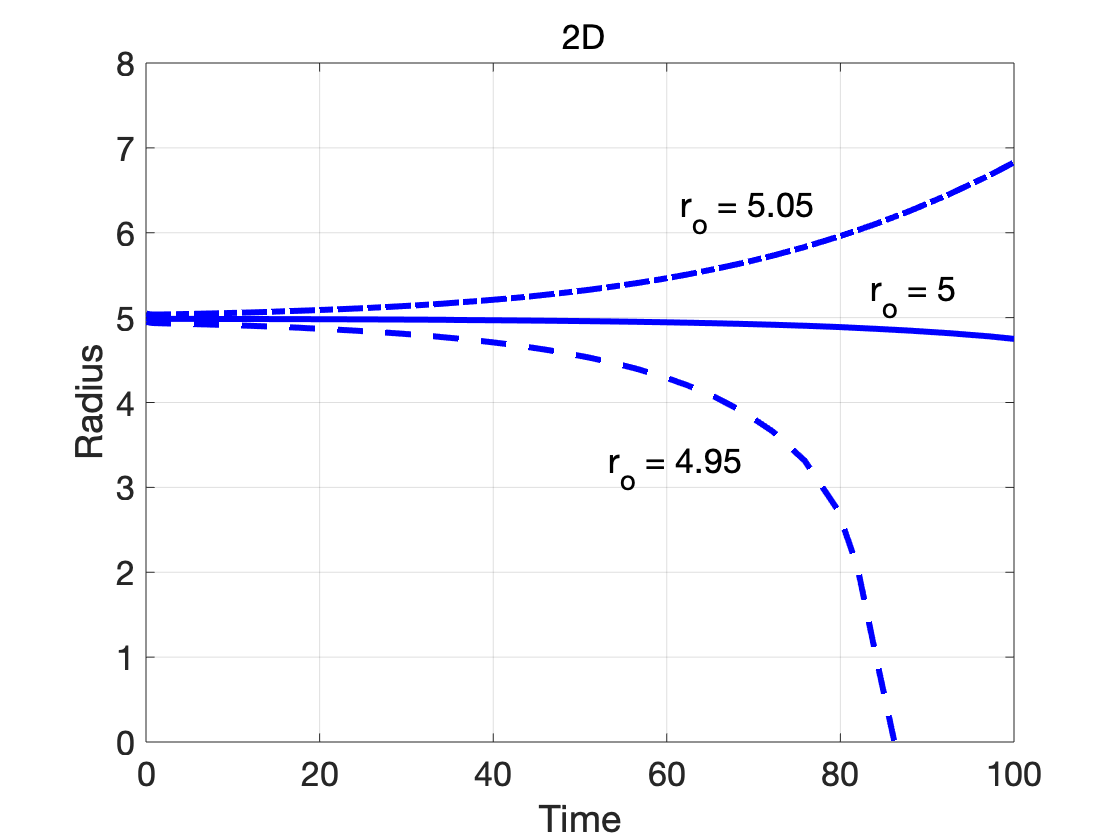
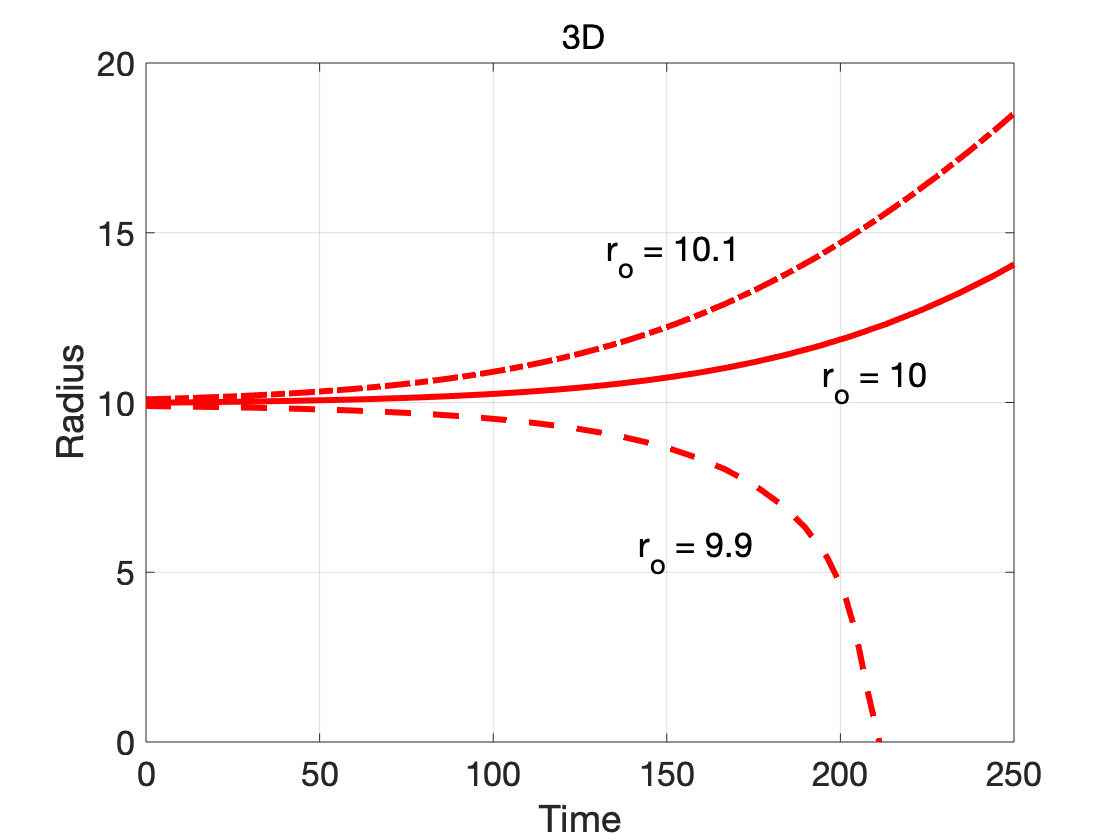
The dependence on dimensionality is further illustrated by considering cases where the initial radius is close to the critical radius:
We used the results from Benchmark Problem 1a and Problem 1b to analyze the effect of boundary conditions. In addition, we solved for Cahn-Hilliard dynamics under the same initial condition and simulation parameters as problem 1 but using mixed boundary conditions, i.e., different boundary conditions for each boundary. We compare the results for each case at simulation time t = 1000. The simulations were carried out in the PRISMS-PF framework using a uniform square mesh with

As can be seen in the figure above, for periodic boundary boundaries the
Carry out a convergence study on the interfacial width. Include impact on all coupled physics. (Demonstrate how to do it on PFHub).
As an example of a mesh convergence study, we can consider Benchmark Problem 1 from the Phase-Field Community Hub. In this problem, which models spinodal decomposition using the Cahn-Hilliard equation, the width of the diffuse interface is 4.47, as defined by the Cahn-Hilliard equation and physical parameters in the problem statement. Given this interface width, we need to ensure there are a sufficient number of grid points (for finite difference schemes) or mesh elements (for finite element or finite volume schemes) through the diffuse interface to adequately resolve the variation of the composition order parameter.
In Problem 1b, a square domain with dimensions
The simulation initial conditions and the microstructures at
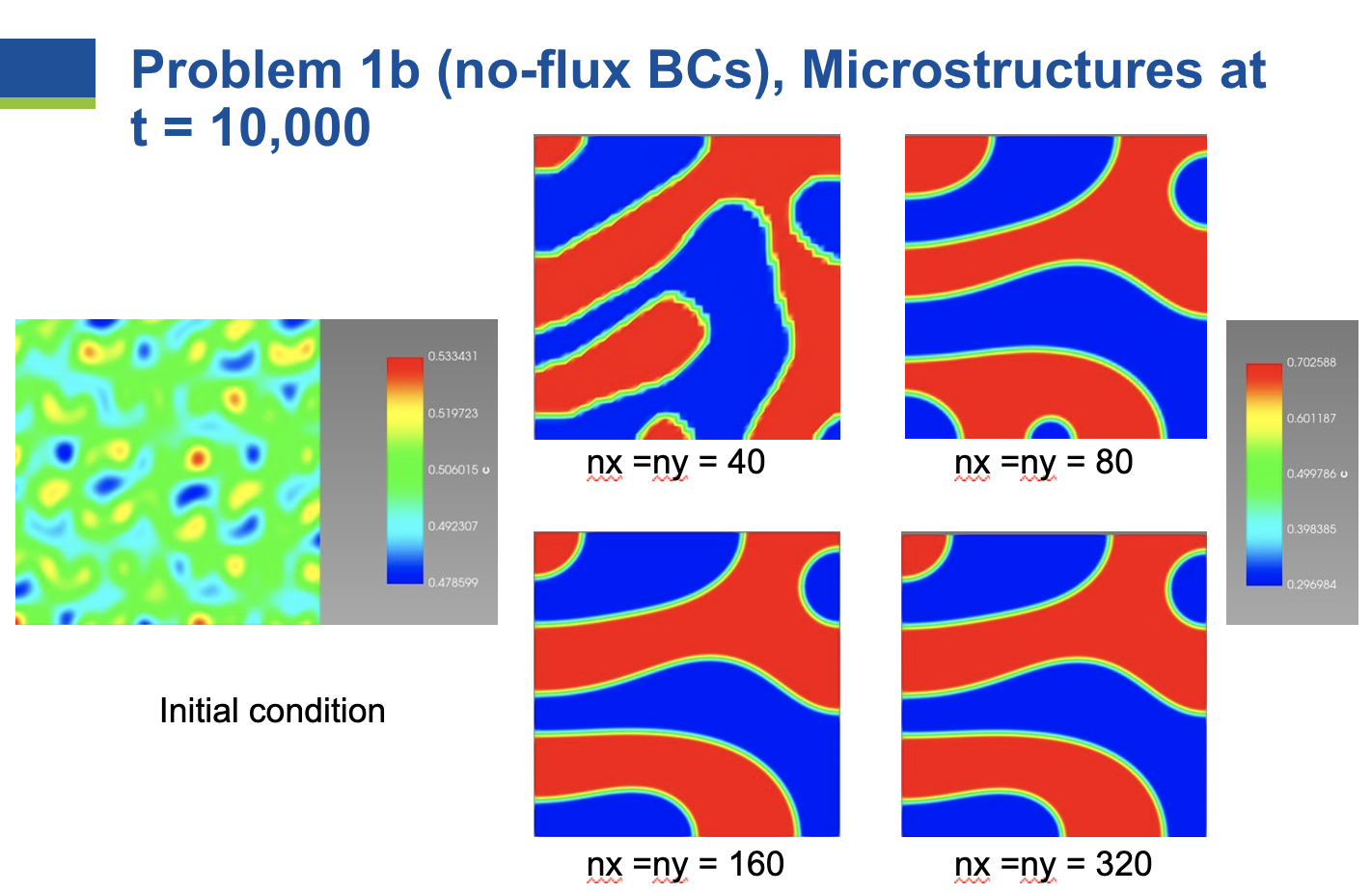
As the number of elements in each direction is increased from 40 to 80 to 160, changes in the microstructure are observed. However, once the number of elements increases to 320, no further changes are observed in the microstructure. Therefore, the problem is converged with respect to mesh resolution at
Carry out time step convergence studies. Try higher-order schemes, adaptive time stepping, etc. For explicit time integration, know your stability limit.
For codes that use explicit time integration, there is a maximum value of the time step beyond which the solution becomes numerically unstable. This stability limit can be determined by the Courant–Friedrichs–Lewy (CFL) condition and, in general, it strongly depends on the order of the spatial derivatives. Below we show the simulation results of Benchmark Problem 1b using time step values slightly below and slightly above the stability limit. We employed a forward Euler time-integration scheme and spatially discretized the system using
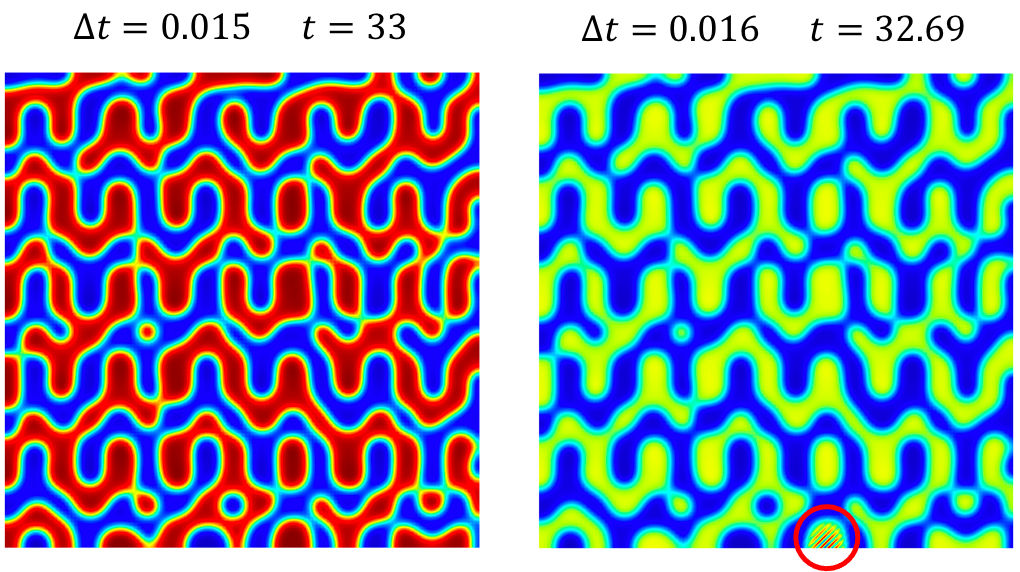
Codes that use implicit time stepping schemes may have fewer restrictions with respect to stability as time step size is increased, depending on the problem. However, discretization error still occurs in implicit schemes and increases with the size of the time step taken. Therefore, a convergence study should be carried out to ensure that the size of the time step does not affect the simulation results. As an example, we can again consider Benchmark Problem 1 from the Phase-Field Community Hub. Problem 1b was solved with the phase-field module from the MOOSE framework using

Adaptive time stepping can be useful to increase the time step size during time periods in the simulation where there are fewer microstructural changes, particularly for codes that use implicit time stepping schemes. However, convergence must still be checked for the parameters of the time stepping scheme being used. An example is the IterationAdaptiveDt time stepping scheme used in the MOOSE framework. This scheme attempts to increase or decrease the time step to keep the solver using a certain number of nonlinear iterations (controlled by the parameter optimal_iterations), within a window or plus or minus the parameter iteration_window. Higher values of optimal_iterations parameter result in higher time steps, and with that comes the risk of discretization error changing simulation results. As shown in the following, for Problem 1b, optimal_iterations values of 6 or 8 gave results consistent with the converged time step of 0.5, but when optimal_iterations was significantly increased to 15, changes in the microstructure resulted.

- Assume your results are wrong until you prove to yourself they are right
- Test rotations, translations, etc.; Purposely misalign problem with the mesh and see impact of result
Oftentimes, the results of the phase field simulations are sensitive to the orientation and alignment of the key microstructural features with the mesh/grid points. To demonstrate this we pick a simple solidification problem with dendritic structure formation. In this case, we utilize the solidification example from the MOOSE-based phase field module. This example problem can quickly demonstrate dendritic structure formation including the formation of secondary dendritic arms in a computationally cost-effective manner. Here, we use 4-fold symmetry of the structure and vary the reference angles to misorient the dendritic arms with respect to the mesh. Dendritic structures corresponding to 0 and 45 degree reference angle is presented below:


It is noteworthy that the shape of the dendrite varies with orientation (as observed by the difference in the dendrite center). For better comparison, we rotate the

This highlights the slight differences between the dendrite shapes, especially the center and the secondary dendritic arms. Additionally, the growth rate of the solid also varies with orientation as observed by the change in solid area fraction over time:
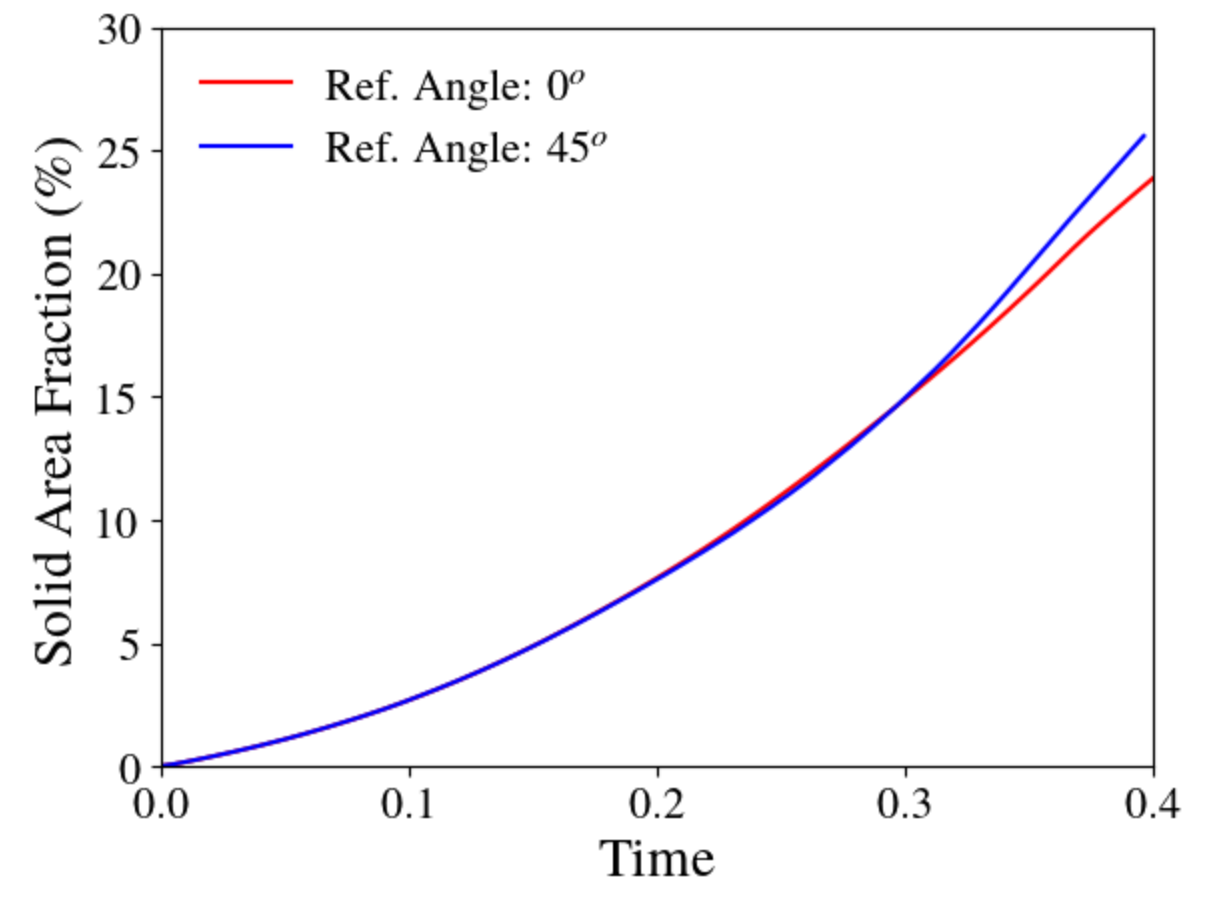
These effects are also influenced by the discretization of the mesh. Therefore, it is important to check the effect of orientation by misaligning the grids.
The amount of time the simulation should be run depends on the science or engineering question to be answered, and on the system being studied. For many classic phase-field problems such as grain growth and coarsening, a characteristic feature size of the system increases with time, and the progress of microstructural evolution slows as the characteristic feature size increases. For example, in grain growth, at long times the mean grain diameter
It is also useful to be aware that the system may reach a metastable or stable equilibrium state with respect to system energy, in which case no further microstructural evolution will occur for increasing simulation time. In the grain growth example, if the system evolves to a single grain, stable equilbrium has been reached. If the system evolves to a two-grain configuration with a flat grain boundary between the grains, it has reached a metastable equilibrium; the system could still lower it energy by removing the grain boundary, but in that configuration, there is no kinetic driving force to remove it from the metastable state. To monitor for such possibilities, it is useful for the simulation to periodically output the total free energy of the system; a stable or metastable equilibrium state is indicated by a constant free energy with respect to time.
- Home
- Benchmark Presentations
- Peter Voorhees Phase Field Lectures
- Phase-Field Method Recommended Practices
- Workshop Presentations
- Miscellaneous