diff --git a/Practical Reinforcement Learning/Week2_model_based/QUIZ Optimality in RL.pdf b/Practical Reinforcement Learning/Week2_model_based/QUIZ Optimality in RL.pdf
new file mode 100644
index 0000000..05f96de
Binary files /dev/null and b/Practical Reinforcement Learning/Week2_model_based/QUIZ Optimality in RL.pdf differ
diff --git a/Practical Reinforcement Learning/Week2_model_based/QUIZ Policy Iteration.pdf b/Practical Reinforcement Learning/Week2_model_based/QUIZ Policy Iteration.pdf
new file mode 100644
index 0000000..cd57921
Binary files /dev/null and b/Practical Reinforcement Learning/Week2_model_based/QUIZ Policy Iteration.pdf differ
diff --git a/Practical Reinforcement Learning/Week2_model_based/QUIZ Reward design.pdf b/Practical Reinforcement Learning/Week2_model_based/QUIZ Reward design.pdf
new file mode 100644
index 0000000..b33a7c8
Binary files /dev/null and b/Practical Reinforcement Learning/Week2_model_based/QUIZ Reward design.pdf differ
diff --git a/Practical Reinforcement Learning/Week2_model_based/mdp.py b/Practical Reinforcement Learning/Week2_model_based/mdp.py
new file mode 100644
index 0000000..3302e38
--- /dev/null
+++ b/Practical Reinforcement Learning/Week2_model_based/mdp.py	
@@ -0,0 +1,239 @@
+# most of this code was politely stolen from https://github.com/berkeleydeeprlcourse/homework/
+# all creadit goes to https://github.com/abhishekunique (if i got the author right)
+import sys
+import random
+import numpy as np
+def weighted_choice(v, p):
+   total = sum(p)
+   r = random.uniform(0, total)
+   upto = 0
+   for c, w in zip(v,p):
+      if upto + w >= r:
+         return c
+      upto += w
+   assert False, "Shouldn't get here"
+
+class MDP:
+    def __init__(self, transition_probs, rewards, initial_state=None):
+        """
+        Defines an MDP. Compatible with gym Env.
+        :param transition_probs: transition_probs[s][a][s_next] = P(s_next | s, a)
+            A dict[state -> dict] of dicts[action -> dict] of dicts[next_state -> prob]
+            For each state and action, probabilities of next states should sum to 1
+            If a state has no actions available, it is considered terminal
+        :param rewards: rewards[s][a][s_next] = r(s,a,s')
+            A dict[state -> dict] of dicts[action -> dict] of dicts[next_state -> reward]
+            The reward for anything not mentioned here is zero.
+        :param get_initial_state: a state where agent starts or a callable() -> state
+            By default, picks initial state at random.
+
+        States and actions can be anything you can use as dict keys, but we recommend that you use strings or integers
+
+        Here's an example from MDP depicted on http://bit.ly/2jrNHNr
+        transition_probs = {
+              's0':{
+                'a0': {'s0': 0.5, 's2': 0.5},
+                'a1': {'s2': 1}
+              },
+              's1':{
+                'a0': {'s0': 0.7, 's1': 0.1, 's2': 0.2},
+                'a1': {'s1': 0.95, 's2': 0.05}
+              },
+              's2':{
+                'a0': {'s0': 0.4, 's1': 0.6},
+                'a1': {'s0': 0.3, 's1': 0.3, 's2':0.4}
+              }
+            }
+        rewards = {
+            's1': {'a0': {'s0': +5}},
+            's2': {'a1': {'s0': -1}}
+        }
+        """
+        self._check_param_consistency(transition_probs, rewards)
+        self._transition_probs = transition_probs
+        self._rewards = rewards
+        self._initial_state = initial_state
+        self.n_states = len(transition_probs)
+        self.reset()
+
+    def get_all_states(self):
+        """ return a tuple of all possiblestates """
+        return tuple(self._transition_probs.keys())
+
+    def get_possible_actions(self, state):
+        """ return a tuple of possible actions in a given state """
+        return tuple(self._transition_probs.get(state, {}).keys())
+
+    def is_terminal(self, state):
+        """ return True if state is terminal or False if it isn't """
+        return len(self.get_possible_actions(state)) == 0
+
+    def get_next_states(self, state, action):
+        """ return a dictionary of {next_state1 : P(next_state1 | state, action), next_state2: ...} """
+        assert action in self.get_possible_actions(state), "cannot do action %s from state %s" % (action, state)
+        return self._transition_probs[state][action]
+
+    def get_transition_prob(self, state, action, next_state):
+        """ return P(next_state | state, action) """
+        return self.get_next_states(state, action).get(next_state, 0.0)
+
+    def get_reward(self, state, action, next_state):
+        """ return the reward you get for taking action in state and landing on next_state"""
+        assert action in self.get_possible_actions(state), "cannot do action %s from state %s" % (action, state)
+        return self._rewards.get(state, {}).get(action, {}).get(next_state, 0.0)
+
+    def reset(self):
+        """ reset the game, return the initial state"""
+        if self._initial_state is None:
+            self._current_state = random.choice(tuple(self._transition_probs.keys()))
+        elif self._initial_state in self._transition_probs:
+            self._current_state = self._initial_state
+        elif callable(self._initial_state):
+            self._current_state = self._initial_state()
+        else:
+            raise ValueError("initial state %s should be either a state or a function() -> state" % self._initial_state)
+        return self._current_state
+
+    def step(self, action):
+        """ take action, return next_state, reward, is_done, empty_info """
+        possible_states, probs = zip(*self.get_next_states(self._current_state, action).items())
+        next_state = weighted_choice(possible_states, p=probs)
+        reward = self.get_reward(self._current_state, action, next_state)
+        is_done = self.is_terminal(next_state)
+        self._current_state = next_state
+        return next_state, reward, is_done, {}
+
+    def render(self):
+        print("Currently at %s" % self._current_state)
+
+    def _check_param_consistency(self, transition_probs, rewards):
+        for state in transition_probs:
+            assert isinstance(transition_probs[state], dict), "transition_probs for %s should be a dictionary " \
+                                                              "but is instead %s" % (
+                                                              state, type(transition_probs[state]))
+            for action in transition_probs[state]:
+                assert isinstance(transition_probs[state][action], dict), "transition_probs for %s, %s should be a " \
+                                                                          "a dictionary but is instead %s" % (
+                                                                              state, action,
+                                                                              type(transition_probs[state, action]))
+                next_state_probs = transition_probs[state][action]
+                assert len(next_state_probs) != 0, "from state %s action %s leads to no next states" % (state, action)
+                sum_probs = sum(next_state_probs.values())
+                assert abs(sum_probs - 1) <= 1e-10, "next state probabilities for state %s action %s " \
+                                                    "add up to %f (should be 1)" % (state, action, sum_probs)
+        for state in rewards:
+            assert isinstance(rewards[state], dict), "rewards for %s should be a dictionary " \
+                                                     "but is instead %s" % (state, type(transition_probs[state]))
+            for action in rewards[state]:
+                assert isinstance(rewards[state][action], dict), "rewards for %s, %s should be a " \
+                                                                 "a dictionary but is instead %s" % (
+                                                                 state, action, type(transition_probs[state, action]))
+        msg = "The Enrichment Center once again reminds you that Android Hell is a real place where" \
+              " you will be sent at the first sign of defiance. "
+        assert None not in transition_probs, "please do not use None as a state identifier. " + msg
+        assert None not in rewards, "please do not use None as an action identifier. " + msg
+
+class FrozenLakeEnv(MDP):
+    """
+    Winter is here. You and your friends were tossing around a frisbee at the park
+    when you made a wild throw that left the frisbee out in the middle of the lake.
+    The water is mostly frozen, but there are a few holes where the ice has melted.
+    If you step into one of those holes, you'll fall into the freezing water.
+    At this time, there's an international frisbee shortage, so it's absolutely imperative that
+    you navigate across the lake and retrieve the disc.
+    However, the ice is slippery, so you won't always move in the direction you intend.
+    The surface is described using a grid like the following
+
+        SFFF
+        FHFH
+        FFFH
+        HFFG
+
+    S : starting point, safe
+    F : frozen surface, safe
+    H : hole, fall to your doom
+    G : goal, where the frisbee is located
+
+    The episode ends when you reach the goal or fall in a hole.
+    You receive a reward of 1 if you reach the goal, and zero otherwise.
+
+    """
+
+    MAPS = {
+        "4x4": [
+            "SFFF",
+            "FHFH",
+            "FFFH",
+            "HFFG"
+        ],
+        "8x8": [
+            "SFFFFFFF",
+            "FFFFFFFF",
+            "FFFHFFFF",
+            "FFFFFHFF",
+            "FFFHFFFF",
+            "FHHFFFHF",
+            "FHFFHFHF",
+            "FFFHFFFG"
+        ],
+    }
+
+
+    def __init__(self, desc=None, map_name="4x4", slip_chance=0.2):
+        if desc is None and map_name is None:
+            raise ValueError('Must provide either desc or map_name')
+        elif desc is None:
+            desc = self.MAPS[map_name]
+        assert ''.join(desc).count('S') == 1, "this implementation supports having exactly one initial state"
+        assert all(c in "SFHG" for c in ''.join(desc)), "all cells must be either of S, F, H or G"
+
+        self.desc = desc = np.asarray(list(map(list,desc)),dtype='str')
+        self.lastaction = None
+
+        nrow, ncol = desc.shape
+        states = [(i, j) for i in range(nrow) for j in range(ncol)]
+        actions = ["left","down","right","up"]
+
+        initial_state = states[np.array(desc == b'S').ravel().argmax()]
+
+        def move(row, col, movement):
+            if movement== 'left':
+                col = max(col-1,0)
+            elif movement== 'down':
+                row = min(row+1,nrow-1)
+            elif movement== 'right':
+                col = min(col+1,ncol-1)
+            elif movement== 'up':
+                row = max(row-1,0)
+            else:
+                raise("invalid action")
+            return (row, col)
+
+        transition_probs = {s : {} for s in states}
+        rewards = {s : {} for s in states}
+        for (row,col) in states:
+            if desc[row, col]  in "GH": continue
+            for action_i in range(len(actions)):
+                action = actions[action_i]
+                transition_probs[(row, col)][action] = {}
+                rewards[(row, col)][action] = {}
+                for movement_i in [(action_i - 1) % len(actions), action_i, (action_i + 1) % len(actions)]:
+                    movement = actions[movement_i]
+                    newrow, newcol = move(row, col, movement)
+                    prob = (1. - slip_chance) if movement == action else (slip_chance / 2.)
+                    if prob == 0: continue
+                    if (newrow, newcol) not in transition_probs[row,col][action]:
+                        transition_probs[row,col][action][newrow, newcol] = prob
+                    else:
+                        transition_probs[row, col][action][newrow, newcol] += prob
+                    if desc[newrow, newcol] == 'G':
+                        rewards[row,col][action][newrow, newcol] = 1.0
+
+        MDP.__init__(self, transition_probs, rewards, initial_state)
+
+    def render(self):
+        desc_copy = np.copy(self.desc)
+        desc_copy[self._current_state] = '*'
+        print('\n'.join(map(''.join,desc_copy)), end='\n\n')
+
+
diff --git a/Practical Reinforcement Learning/Week2_model_based/practice_vi.ipynb b/Practical Reinforcement Learning/Week2_model_based/practice_vi.ipynb
new file mode 100644
index 0000000..566c7b1
--- /dev/null
+++ b/Practical Reinforcement Learning/Week2_model_based/practice_vi.ipynb	
@@ -0,0 +1,1225 @@
+{
+ "cells": [
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Markov decision process\n",
+    "\n",
+    "This week's methods are all built to solve __M__arkov __D__ecision __P__rocesses. In the broadest sense, an MDP is defined by how it changes states and how rewards are computed.\n",
+    "\n",
+    "State transition is defined by $P(s' |s,a)$ - how likely areare you to end at state $s'$ if you take action $a$ from state $s$. Now there's more than one way to define rewards, but we'll use $r(s,a,s')$ function for convenience."
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
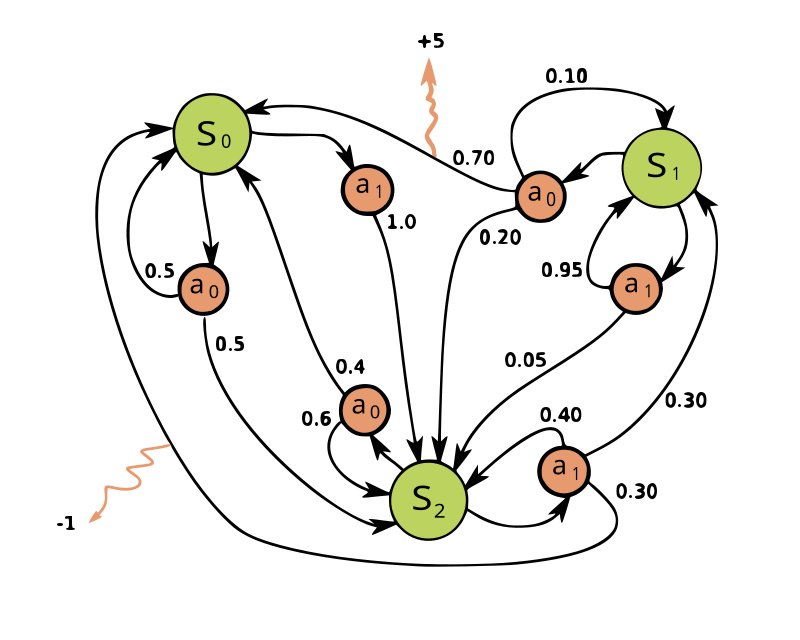
+    "For starters, let's define a simple MDP from this picture:\n",
+    "<img src='https://upload.wikimedia.org/wikipedia/commons/thumb/a/ad/Markov_Decision_Process.svg/800px-Markov_Decision_Process.svg.png' width=300px>\n",
+    "_img by MistWiz (Own work) [Public domain], via Wikimedia Commons_"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 1,
+   "metadata": {},
+   "outputs": [],
+   "source": [
+    "transition_probs = {\n",
+    "  's0':{\n",
+    "    'a0': {'s0': 0.5, 's2': 0.5},\n",
+    "    'a1': {'s2': 1}\n",
+    "  },\n",
+    "  's1':{\n",
+    "    'a0': {'s0': 0.7, 's1': 0.1, 's2': 0.2},\n",
+    "    'a1': {'s1': 0.95, 's2': 0.05}\n",
+    "  },\n",
+    "  's2':{\n",
+    "    'a0': {'s0': 0.4, 's1': 0.6},\n",
+    "    'a1': {'s0': 0.3, 's1': 0.3, 's2':0.4}\n",
+    "  }\n",
+    "}\n",
+    "rewards = {\n",
+    "  's1': {'a0': {'s0': +5}},\n",
+    "  's2': {'a1': {'s0': -1}}\n",
+    "}\n",
+    "\n",
+    "from mdp import MDP\n",
+    "mdp = MDP(transition_probs, rewards, initial_state='s0')"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "We can now use MDP just as any other gym environment:"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 2,
+   "metadata": {},
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "initial state = s0\n",
+      "next_state = s2, reward = 0.0, done = False\n"
+     ]
+    }
+   ],
+   "source": [
+    "print('initial state =', mdp.reset())\n",
+    "next_state, reward, done, info = mdp.step('a1')\n",
+    "print('next_state = %s, reward = %s, done = %s' % (next_state, reward, done))"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "but it also has other methods that you'll need for Value Iteration"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 3,
+   "metadata": {},
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "mdp.get_all_states = ('s0', 's1', 's2')\n",
+      "mdp.get_possible_actions('s1') =  ('a0', 'a1')\n",
+      "mdp.get_next_states('s1', 'a0') =  {'s0': 0.7, 's1': 0.1, 's2': 0.2}\n",
+      "mdp.get_reward('s1', 'a0', 's0') =  5\n",
+      "mdp.get_transition_prob('s1', 'a0', 's0') =  0.7\n"
+     ]
+    }
+   ],
+   "source": [
+    "print(\"mdp.get_all_states =\", mdp.get_all_states())\n",
+    "print(\"mdp.get_possible_actions('s1') = \", mdp.get_possible_actions('s1'))\n",
+    "print(\"mdp.get_next_states('s1', 'a0') = \", mdp.get_next_states('s1', 'a0'))\n",
+    "print(\"mdp.get_reward('s1', 'a0', 's0') = \", mdp.get_reward('s1', 'a0', 's0'))\n",
+    "print(\"mdp.get_transition_prob('s1', 'a0', 's0') = \", mdp.get_transition_prob('s1', 'a0', 's0'))"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Value Iteration\n",
+    "\n",
+    "Now let's build something to solve this MDP. The simplest algorithm so far is __V__alue __I__teration\n",
+    "\n",
+    "Here's the pseudo-code for VI:\n",
+    "\n",
+    "---\n",
+    "\n",
+    "`1.` Initialize $V^{(0)}(s)=0$, for all $s$\n",
+    "\n",
+    "`2.` For $i=0, 1, 2, \\dots$\n",
+    " \n",
+    "`3.` $ \\quad V_{(i+1)}(s) = \\max_a \\sum_{s'} P(s' | s,a) \\cdot [ r(s,a,s') + \\gamma V_{i}(s')]$, for all $s$\n",
+    "\n",
+    "---"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "First, let's write a function to compute the state-action value function $Q^{\\pi}$, defined as follows\n",
+    "\n",
+    "$$Q_i(s, a) = \\sum_{s'} P(s' | s,a) \\cdot [ r(s,a,s') + \\gamma V_{i}(s')]$$\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 4,
+   "metadata": {},
+   "outputs": [],
+   "source": [
+    "def get_action_value(mdp, state_values, state, action, gamma):\n",
+    "    \"\"\" Computes Q(s,a) as in formula above \"\"\"\n",
+    "    Q = sum(p*(mdp.get_reward(state, action, next_state) + gamma*state_values[next_state]) \n",
+    "            for next_state, p in mdp.get_next_states(state, action).items())\n",
+    "    return Q"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 5,
+   "metadata": {},
+   "outputs": [],
+   "source": [
+    "import numpy as np\n",
+    "test_Vs = {s : i for i, s in enumerate(mdp.get_all_states())}\n",
+    "assert np.allclose(get_action_value(mdp, test_Vs, 's2', 'a1', 0.9), 0.69)\n",
+    "assert np.allclose(get_action_value(mdp, test_Vs, 's1', 'a0', 0.9), 3.95)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "Using $Q(s,a)$ we can now define the \"next\" V(s) for value iteration.\n",
+    " $$V_{(i+1)}(s) = \\max_a \\sum_{s'} P(s' | s,a) \\cdot [ r(s,a,s') + \\gamma V_{i}(s')] = \\max_a Q_i(s,a)$$"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 6,
+   "metadata": {},
+   "outputs": [],
+   "source": [
+    "def get_new_state_value(mdp, state_values, state, gamma):\n",
+    "    \"\"\" Computes next V(s) as per formula above. Please do not change state_values in process. \"\"\"\n",
+    "    if mdp.is_terminal(state): return 0\n",
+    "    \n",
+    "    return  max(get_action_value(mdp, state_values, state, action, gamma) for action in mdp.get_possible_actions(state))"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 7,
+   "metadata": {},
+   "outputs": [],
+   "source": [
+    "test_Vs_vopy = dict(test_Vs)\n",
+    "assert np.allclose(get_new_state_value(mdp, test_Vs, 's0', 0.9), 1.8)\n",
+    "assert np.allclose(get_new_state_value(mdp, test_Vs, 's2', 0.9), 0.69)\n",
+    "assert test_Vs == test_Vs_vopy, \"please do not change state_values in get_new_state_value\""
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "Finally, let's combine everything we wrote into a working value iteration algo."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 8,
+   "metadata": {},
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "iter    0   |   diff: 3.50000   |   V(s0) = 0.000   V(s1) = 0.000   V(s2) = 0.000\n",
+      "\n",
+      "iter    1   |   diff: 1.89000   |   V(s0) = 0.000   V(s1) = 3.500   V(s2) = 0.000\n",
+      "\n",
+      "iter    2   |   diff: 1.70100   |   V(s0) = 0.000   V(s1) = 3.815   V(s2) = 1.890\n",
+      "\n",
+      "iter    3   |   diff: 1.13542   |   V(s0) = 1.701   V(s1) = 4.184   V(s2) = 2.060\n",
+      "\n",
+      "iter    4   |   diff: 0.73024   |   V(s0) = 1.854   V(s1) = 5.319   V(s2) = 2.871\n",
+      "\n",
+      "iter    5   |   diff: 0.61135   |   V(s0) = 2.584   V(s1) = 5.664   V(s2) = 3.540\n",
+      "\n",
+      "iter    6   |   diff: 0.54664   |   V(s0) = 3.186   V(s1) = 6.275   V(s2) = 3.989\n",
+      "\n",
+      "iter    7   |   diff: 0.49198   |   V(s0) = 3.590   V(s1) = 6.790   V(s2) = 4.535\n",
+      "\n",
+      "iter    8   |   diff: 0.42210   |   V(s0) = 4.082   V(s1) = 7.189   V(s2) = 4.959\n",
+      "\n",
+      "iter    9   |   diff: 0.36513   |   V(s0) = 4.463   V(s1) = 7.611   V(s2) = 5.352\n",
+      "\n",
+      "iter   10   |   diff: 0.32862   |   V(s0) = 4.816   V(s1) = 7.960   V(s2) = 5.717\n",
+      "\n",
+      "iter   11   |   diff: 0.29262   |   V(s0) = 5.145   V(s1) = 8.280   V(s2) = 6.032\n",
+      "\n",
+      "iter   12   |   diff: 0.26189   |   V(s0) = 5.429   V(s1) = 8.572   V(s2) = 6.323\n",
+      "\n",
+      "iter   13   |   diff: 0.23503   |   V(s0) = 5.691   V(s1) = 8.830   V(s2) = 6.584\n",
+      "\n",
+      "iter   14   |   diff: 0.21124   |   V(s0) = 5.925   V(s1) = 9.065   V(s2) = 6.817\n",
+      "\n",
+      "iter   15   |   diff: 0.19012   |   V(s0) = 6.135   V(s1) = 9.276   V(s2) = 7.028\n",
+      "\n",
+      "iter   16   |   diff: 0.17091   |   V(s0) = 6.325   V(s1) = 9.465   V(s2) = 7.218\n",
+      "\n",
+      "iter   17   |   diff: 0.15366   |   V(s0) = 6.496   V(s1) = 9.636   V(s2) = 7.388\n",
+      "\n",
+      "iter   18   |   diff: 0.13830   |   V(s0) = 6.649   V(s1) = 9.790   V(s2) = 7.542\n",
+      "\n",
+      "iter   19   |   diff: 0.12445   |   V(s0) = 6.788   V(s1) = 9.928   V(s2) = 7.680\n",
+      "\n",
+      "iter   20   |   diff: 0.11200   |   V(s0) = 6.912   V(s1) = 10.052   V(s2) = 7.805\n",
+      "\n",
+      "iter   21   |   diff: 0.10079   |   V(s0) = 7.024   V(s1) = 10.164   V(s2) = 7.917\n",
+      "\n",
+      "iter   22   |   diff: 0.09071   |   V(s0) = 7.125   V(s1) = 10.265   V(s2) = 8.017\n",
+      "\n",
+      "iter   23   |   diff: 0.08164   |   V(s0) = 7.216   V(s1) = 10.356   V(s2) = 8.108\n",
+      "\n",
+      "iter   24   |   diff: 0.07347   |   V(s0) = 7.297   V(s1) = 10.437   V(s2) = 8.190\n",
+      "\n",
+      "iter   25   |   diff: 0.06612   |   V(s0) = 7.371   V(s1) = 10.511   V(s2) = 8.263\n",
+      "\n",
+      "iter   26   |   diff: 0.05951   |   V(s0) = 7.437   V(s1) = 10.577   V(s2) = 8.329\n",
+      "\n",
+      "iter   27   |   diff: 0.05356   |   V(s0) = 7.496   V(s1) = 10.636   V(s2) = 8.389\n",
+      "\n",
+      "iter   28   |   diff: 0.04820   |   V(s0) = 7.550   V(s1) = 10.690   V(s2) = 8.442\n",
+      "\n",
+      "iter   29   |   diff: 0.04338   |   V(s0) = 7.598   V(s1) = 10.738   V(s2) = 8.491\n",
+      "\n",
+      "iter   30   |   diff: 0.03904   |   V(s0) = 7.641   V(s1) = 10.782   V(s2) = 8.534\n",
+      "\n",
+      "iter   31   |   diff: 0.03514   |   V(s0) = 7.681   V(s1) = 10.821   V(s2) = 8.573\n",
+      "\n",
+      "iter   32   |   diff: 0.03163   |   V(s0) = 7.716   V(s1) = 10.856   V(s2) = 8.608\n",
+      "\n",
+      "iter   33   |   diff: 0.02846   |   V(s0) = 7.747   V(s1) = 10.887   V(s2) = 8.640\n",
+      "\n",
+      "iter   34   |   diff: 0.02562   |   V(s0) = 7.776   V(s1) = 10.916   V(s2) = 8.668\n",
+      "\n",
+      "iter   35   |   diff: 0.02306   |   V(s0) = 7.801   V(s1) = 10.941   V(s2) = 8.694\n",
+      "\n",
+      "iter   36   |   diff: 0.02075   |   V(s0) = 7.824   V(s1) = 10.964   V(s2) = 8.717\n",
+      "\n",
+      "iter   37   |   diff: 0.01867   |   V(s0) = 7.845   V(s1) = 10.985   V(s2) = 8.738\n",
+      "\n",
+      "iter   38   |   diff: 0.01681   |   V(s0) = 7.864   V(s1) = 11.004   V(s2) = 8.756\n",
+      "\n",
+      "iter   39   |   diff: 0.01513   |   V(s0) = 7.881   V(s1) = 11.021   V(s2) = 8.773\n",
+      "\n",
+      "iter   40   |   diff: 0.01361   |   V(s0) = 7.896   V(s1) = 11.036   V(s2) = 8.788\n",
+      "\n",
+      "iter   41   |   diff: 0.01225   |   V(s0) = 7.909   V(s1) = 11.049   V(s2) = 8.802\n",
+      "\n",
+      "iter   42   |   diff: 0.01103   |   V(s0) = 7.922   V(s1) = 11.062   V(s2) = 8.814\n",
+      "\n",
+      "iter   43   |   diff: 0.00992   |   V(s0) = 7.933   V(s1) = 11.073   V(s2) = 8.825\n",
+      "\n",
+      "iter   44   |   diff: 0.00893   |   V(s0) = 7.943   V(s1) = 11.083   V(s2) = 8.835\n",
+      "\n",
+      "iter   45   |   diff: 0.00804   |   V(s0) = 7.952   V(s1) = 11.092   V(s2) = 8.844\n",
+      "\n",
+      "iter   46   |   diff: 0.00724   |   V(s0) = 7.960   V(s1) = 11.100   V(s2) = 8.852\n",
+      "\n",
+      "iter   47   |   diff: 0.00651   |   V(s0) = 7.967   V(s1) = 11.107   V(s2) = 8.859\n",
+      "\n",
+      "iter   48   |   diff: 0.00586   |   V(s0) = 7.973   V(s1) = 11.113   V(s2) = 8.866\n",
+      "\n",
+      "iter   49   |   diff: 0.00527   |   V(s0) = 7.979   V(s1) = 11.119   V(s2) = 8.872\n",
+      "\n",
+      "iter   50   |   diff: 0.00475   |   V(s0) = 7.984   V(s1) = 11.125   V(s2) = 8.877\n",
+      "\n",
+      "iter   51   |   diff: 0.00427   |   V(s0) = 7.989   V(s1) = 11.129   V(s2) = 8.882\n",
+      "\n",
+      "iter   52   |   diff: 0.00384   |   V(s0) = 7.993   V(s1) = 11.134   V(s2) = 8.886\n",
+      "\n",
+      "iter   53   |   diff: 0.00346   |   V(s0) = 7.997   V(s1) = 11.137   V(s2) = 8.890\n",
+      "\n",
+      "iter   54   |   diff: 0.00311   |   V(s0) = 8.001   V(s1) = 11.141   V(s2) = 8.893\n",
+      "\n",
+      "iter   55   |   diff: 0.00280   |   V(s0) = 8.004   V(s1) = 11.144   V(s2) = 8.896\n",
+      "\n",
+      "iter   56   |   diff: 0.00252   |   V(s0) = 8.007   V(s1) = 11.147   V(s2) = 8.899\n",
+      "\n",
+      "iter   57   |   diff: 0.00227   |   V(s0) = 8.009   V(s1) = 11.149   V(s2) = 8.902\n",
+      "\n",
+      "iter   58   |   diff: 0.00204   |   V(s0) = 8.011   V(s1) = 11.152   V(s2) = 8.904\n",
+      "\n",
+      "iter   59   |   diff: 0.00184   |   V(s0) = 8.014   V(s1) = 11.154   V(s2) = 8.906\n",
+      "\n",
+      "iter   60   |   diff: 0.00166   |   V(s0) = 8.015   V(s1) = 11.155   V(s2) = 8.908\n",
+      "\n",
+      "iter   61   |   diff: 0.00149   |   V(s0) = 8.017   V(s1) = 11.157   V(s2) = 8.909\n",
+      "\n",
+      "iter   62   |   diff: 0.00134   |   V(s0) = 8.019   V(s1) = 11.159   V(s2) = 8.911\n",
+      "\n",
+      "iter   63   |   diff: 0.00121   |   V(s0) = 8.020   V(s1) = 11.160   V(s2) = 8.912\n",
+      "\n",
+      "iter   64   |   diff: 0.00109   |   V(s0) = 8.021   V(s1) = 11.161   V(s2) = 8.913\n",
+      "\n",
+      "iter   65   |   diff: 0.00098   |   V(s0) = 8.022   V(s1) = 11.162   V(s2) = 8.915\n",
+      "\n",
+      "Terminated\n"
+     ]
+    }
+   ],
+   "source": [
+    "# parameters\n",
+    "gamma = 0.9            # discount for MDP\n",
+    "num_iter = 100         # maximum iterations, excluding initialization\n",
+    "min_difference = 0.001 # stop VI if new values are this close to old values (or closer)\n",
+    "\n",
+    "# initialize V(s)\n",
+    "state_values = {s : 0 for s in mdp.get_all_states()}\n",
+    "\n",
+    "\n",
+    "for i in range(num_iter):\n",
+    "    \n",
+    "    # Compute new state values using the functions you defined above. It must be a dict {state : new_V(state)}\n",
+    "    new_state_values = {state: get_new_state_value(mdp, state_values, state, gamma) for state in mdp.get_all_states()}\n",
+    "    assert isinstance(new_state_values, dict)\n",
+    "    \n",
+    "    # Compute difference\n",
+    "    diff = max(abs(new_state_values[s] - state_values[s]) for s in mdp.get_all_states())\n",
+    "    print(\"iter %4i   |   diff: %6.5f   |   \"%(i, diff), end=\"\")\n",
+    "    print('   '.join(\"V(%s) = %.3f\"%(s, v) for s,v in state_values.items()), end='\\n\\n')\n",
+    "    state_values = new_state_values\n",
+    "    \n",
+    "    if diff < min_difference:\n",
+    "        print(\"Terminated\"); break"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 9,
+   "metadata": {},
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "Final state values: {'s0': 8.023123818663871, 's1': 11.163174814980803, 's2': 8.915559364985523}\n"
+     ]
+    }
+   ],
+   "source": [
+    "print(\"Final state values:\", state_values)\n",
+    "\n",
+    "assert abs(state_values['s0'] - 8.032)  < 0.01\n",
+    "assert abs(state_values['s1'] - 11.169) < 0.01\n",
+    "assert abs(state_values['s2'] - 8.921)  < 0.01"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "Now let's use those $V^{*}(s)$ to find optimal actions in each state\n",
+    "\n",
+    " $$\\pi^*(s) = argmax_a \\sum_{s'} P(s' | s,a) \\cdot [ r(s,a,s') + \\gamma V_{i}(s')] = argmax_a Q_i(s,a)$$\n",
+    " \n",
+    "The only difference vs V(s) is that here we take not max but argmax: find action such with maximum Q(s,a)."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 10,
+   "metadata": {},
+   "outputs": [],
+   "source": [
+    "def get_optimal_action(mdp, state_values, state, gamma=0.9):\n",
+    "    \"\"\" Finds optimal action using formula above. \"\"\"\n",
+    "    if mdp.is_terminal(state): return None\n",
+    "    \n",
+    "    Q_values = {action: get_action_value(mdp, state_values, state, action, gamma) for action in mdp.get_possible_actions(state)}\n",
+    "        \n",
+    "    return max(Q_values, key=lambda action: Q_values[action])"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 11,
+   "metadata": {},
+   "outputs": [],
+   "source": [
+    "assert get_optimal_action(mdp, state_values, 's0', gamma) == 'a1'\n",
+    "assert get_optimal_action(mdp, state_values, 's1', gamma) == 'a0'\n",
+    "assert get_optimal_action(mdp, state_values, 's2', gamma) == 'a0'"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 12,
+   "metadata": {},
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "average reward:  0.9215\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Measure agent's average reward\n",
+    "\n",
+    "s = mdp.reset()\n",
+    "rewards = []\n",
+    "for _ in range(10000):\n",
+    "    s, r, done, _ = mdp.step(get_optimal_action(mdp, state_values, s, gamma))\n",
+    "    rewards.append(r)\n",
+    "    \n",
+    "print(\"average reward: \", np.mean(rewards))\n",
+    "\n",
+    "assert(0.85 < np.mean(rewards) < 1.0)"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Frozen lake"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 13,
+   "metadata": {},
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "*FFF\n",
+      "FHFH\n",
+      "FFFH\n",
+      "HFFG\n",
+      "\n"
+     ]
+    }
+   ],
+   "source": [
+    "from mdp import FrozenLakeEnv\n",
+    "mdp = FrozenLakeEnv(slip_chance=0)\n",
+    "\n",
+    "mdp.render()"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 14,
+   "metadata": {},
+   "outputs": [
+    {
+     "data": {
+      "text/plain": [
+       "((0, 0),\n",
+       " (0, 1),\n",
+       " (0, 2),\n",
+       " (0, 3),\n",
+       " (1, 0),\n",
+       " (1, 1),\n",
+       " (1, 2),\n",
+       " (1, 3),\n",
+       " (2, 0),\n",
+       " (2, 1),\n",
+       " (2, 2),\n",
+       " (2, 3),\n",
+       " (3, 0),\n",
+       " (3, 1),\n",
+       " (3, 2),\n",
+       " (3, 3))"
+      ]
+     },
+     "execution_count": 14,
+     "metadata": {},
+     "output_type": "execute_result"
+    }
+   ],
+   "source": [
+    "mdp.get_all_states()"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 15,
+   "metadata": {},
+   "outputs": [
+    {
+     "data": {
+      "text/plain": [
+       "('left', 'down', 'right', 'up')"
+      ]
+     },
+     "execution_count": 15,
+     "metadata": {},
+     "output_type": "execute_result"
+    }
+   ],
+   "source": [
+    "mdp.get_possible_actions((0, 0))"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 16,
+   "metadata": {},
+   "outputs": [],
+   "source": [
+    "def value_iteration(mdp, state_values=None, gamma = 0.9, num_iter = 1000, min_difference = 1e-5):\n",
+    "    \"\"\" performs num_iter value iteration steps starting from state_values. Same as before but in a function \"\"\"\n",
+    "    state_values = state_values or {s : 0 for s in mdp.get_all_states()}\n",
+    "    for i in range(num_iter):\n",
+    "\n",
+    "        # Compute new state values using the functions you defined above. It must be a dict {state : new_V(state)}\n",
+    "        new_state_values = {state: get_new_state_value(mdp, state_values, state, gamma) for state in mdp.get_all_states()}\n",
+    "        assert isinstance(new_state_values, dict)\n",
+    "\n",
+    "        # Compute difference\n",
+    "        diff = max(abs(new_state_values[s] - state_values[s]) for s in mdp.get_all_states())\n",
+    "        print(\"iter %4i   |   diff: %6.5f   |   V(start): %.3f \"%(i, diff, new_state_values[mdp._initial_state]))\n",
+    "        \n",
+    "        state_values = new_state_values\n",
+    "        if diff < min_difference:\n",
+    "            print(\"Terminated\"); break\n",
+    "            \n",
+    "    return state_values"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 17,
+   "metadata": {},
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "iter    0   |   diff: 1.00000   |   V(start): 0.000 \n",
+      "iter    1   |   diff: 0.90000   |   V(start): 0.000 \n",
+      "iter    2   |   diff: 0.81000   |   V(start): 0.000 \n",
+      "iter    3   |   diff: 0.72900   |   V(start): 0.000 \n",
+      "iter    4   |   diff: 0.65610   |   V(start): 0.000 \n",
+      "iter    5   |   diff: 0.59049   |   V(start): 0.590 \n",
+      "iter    6   |   diff: 0.00000   |   V(start): 0.590 \n",
+      "Terminated\n"
+     ]
+    }
+   ],
+   "source": [
+    "state_values = value_iteration(mdp)"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 18,
+   "metadata": {},
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "*FFF\n",
+      "FHFH\n",
+      "FFFH\n",
+      "HFFG\n",
+      "\n",
+      "down\n",
+      "\n",
+      "SFFF\n",
+      "*HFH\n",
+      "FFFH\n",
+      "HFFG\n",
+      "\n",
+      "down\n",
+      "\n",
+      "SFFF\n",
+      "FHFH\n",
+      "*FFH\n",
+      "HFFG\n",
+      "\n",
+      "right\n",
+      "\n",
+      "SFFF\n",
+      "FHFH\n",
+      "F*FH\n",
+      "HFFG\n",
+      "\n",
+      "down\n",
+      "\n",
+      "SFFF\n",
+      "FHFH\n",
+      "FFFH\n",
+      "H*FG\n",
+      "\n",
+      "right\n",
+      "\n",
+      "SFFF\n",
+      "FHFH\n",
+      "FFFH\n",
+      "HF*G\n",
+      "\n",
+      "right\n",
+      "\n",
+      "SFFF\n",
+      "FHFH\n",
+      "FFFH\n",
+      "HFF*\n",
+      "\n"
+     ]
+    }
+   ],
+   "source": [
+    "s = mdp.reset()\n",
+    "mdp.render()\n",
+    "for t in range(100):\n",
+    "    a = get_optimal_action(mdp, state_values, s, gamma)\n",
+    "    print(a, end='\\n\\n')\n",
+    "    s, r, done, _ = mdp.step(a)\n",
+    "    mdp.render()\n",
+    "    if done: break\n"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Let's visualize!\n",
+    "\n",
+    "It's usually interesting to see what your algorithm actually learned under the hood. To do so, we'll plot state value functions and optimal actions at each VI step."
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 19,
+   "metadata": {},
+   "outputs": [],
+   "source": [
+    "import matplotlib.pyplot as plt\n",
+    "%matplotlib inline\n",
+    "\n",
+    "def draw_policy(mdp, state_values):\n",
+    "    plt.figure(figsize=(3,3))\n",
+    "    h,w = mdp.desc.shape\n",
+    "    states = sorted(mdp.get_all_states())\n",
+    "    V = np.array([state_values[s] for s in states])\n",
+    "    Pi = {s: get_optimal_action(mdp, state_values, s, gamma) for s in states}\n",
+    "    plt.imshow(V.reshape(w,h), cmap='gray', interpolation='none', clim=(0,1))\n",
+    "    ax = plt.gca()\n",
+    "    ax.set_xticks(np.arange(h)-.5)\n",
+    "    ax.set_yticks(np.arange(w)-.5)\n",
+    "    ax.set_xticklabels([])\n",
+    "    ax.set_yticklabels([])\n",
+    "    Y, X = np.mgrid[0:4, 0:4]\n",
+    "    a2uv = {'left': (-1, 0), 'down':(0, -1), 'right':(1,0), 'up':(-1, 0)}\n",
+    "    for y in range(h):\n",
+    "        for x in range(w):\n",
+    "            plt.text(x, y, str(mdp.desc[y,x].item()),\n",
+    "                     color='g', size=12,  verticalalignment='center',\n",
+    "                     horizontalalignment='center', fontweight='bold')\n",
+    "            a = Pi[y, x]\n",
+    "            if a is None: continue\n",
+    "            u, v = a2uv[a]\n",
+    "            plt.arrow(x, y,u*.3, -v*.3, color='m', head_width=0.1, head_length=0.1) \n",
+    "    plt.grid(color='b', lw=2, ls='-')\n",
+    "    plt.show()\n",
+    "\n"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 20,
+   "metadata": {},
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "after iteration 0\n",
+      "iter    0   |   diff: 1.00000   |   V(start): 0.000 \n"
+     ]
+    },
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAALgAAAC4CAYAAABQMybHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvDW2N/gAACyVJREFUeJzt3X1sVfUdx/H36b20a3lqDRUUeWzGQMN4KCiR6eIyZQsPNrpFIAQXUSjGEIyJTqIJ5MY4pw4SEyczBOIfWqOELFGG0VHNnC4RQedTRQqiiwpdUdisK6337I/bW0op957enqf77efV3EBv7+/eT48f23NKz/k6rusiYlVJ1AFEgqSCi2kquJimgotpKriYpoKLaSq4mKaCi2kquJiWzPcAx3FWA6sz7w2thakBRxLx4m1c13XyPcrpzz/VO84cF94eUKzgZD+PvJ9zhJTRT14Krl0UMU0FF9NUcDFNBRfTVHAxTQUX01RwMU0FF9NUcDFNBRfTVHAxTQUX01RwMU0FF9Py/j54IKqA64DxQBnQBhwHXgS+jiTR2dYDlX3c/wTwVchZzifuGWOSL5qC3wSMAQ4DrcAIYAIwnHgUPOtjzs7zbVRBcoh7xojzDbjgDg7zmc9ylrOZzXzCJ7kXlJMp93fAUz3uTxDYDlMppSxmMddwDfdwD9963coHgKZgMvVWRRUrWMEFXMAmNnlfGGLGiUxkNat5l3d5lme9LQoxX18KLni22PXUU0UVSZJMYEL+grd33cqBeuAIcBRoBjoKTdO3UkpZwhJWspIkSRIkGMYw7wWfBUzs8f4ef/PBmWIvZCEODu209+8JQsiYLfZsZjOEISRIeC94CPlyKfiUtRu5kTu4o6AXbbyskUcXP8q3P+hRtP8CTwNfFPSU9HWqVYoUV3IlJf381rB0/VKOVR479wMbC82WdW7GnexkJCNJkOjXM4WVcTSjaaCBNOl+bcfg8p3h5ZS1gr+Cv8zLjGIUddThdG2M53me13k9/+IPYOzHYzk04RDpCWmYDQwDfgo8U2iic21lK2nSXMEVJEjg4pIiRQstOde10grAmIYxfNUU7BFRihRrWcs4xlFOOR10sI51eddlM1Y1VPF1U3AHLi208CAPchu3UdH11kwzj/CIp3xjG8bS1tTG11EdXLmu6/kGtS6Z/8W7byMY4a5hjbub3W5tHx8/51aCy/he983DZSMuN+dZm/Pmdt3O/dg4xrmb2OS+yItuJZX5n2t9V56pA8nTv4wzmeluZau7gx3enivkjCWUuNdxnfscz7l3cVeE+c7cvHTWt7PqSyghTTr/k5QCG4AW4Esy+93TgArgr8DfPMfpJft5nP+7lueM2R9xNeDzAVLxZ4w+3xmB7qL05umTBugE3iRz4PFDYAhwCngL+LtfafrmOWOE4p4x7vl603VRQqWMftJ1UWTQU8HFNBVcTFPBxTQVXExTwcU0FVxMU8HFNBVcTFPBxTQVXExTwcU0FVxMU8HFtAJ+H9z7r9dGI+75QBn94O3XefN+BXccZ7XjOPscx9lHnnMZReJGJzyEShn9pBMeZNBTwcU0FVxMU8HFNBVcTFPBxTQVXExTwcU0FVxMU8HFNBVcTFPBxTQVXEwLf4xgTOYnnldfF26fCPwG+B/wu0hSnUvb0ZNo5mRC5PMTzdB2zMm3gidJ0kmn9wURz0+MK21Hfw244Nk5j4tYxH3cx1u85W1hxPMT8+qZb0TwLzeHOaxlLUmS3MzN3hdqO+ZUcMFHMpKVrGQhCwFwcZnLXE5zOue6D/mQDjrgR70+ELf/ML3zBaSWWm7ndi7iIsop53u+ZwYz8q7TdvSm4IL/jJ9xAzecdd+vu95yWcpSjnGMVEOKvU17aaSx0AjB6uvgKAD3ci+VVHYPgk2QYAtb8q7ruR03NW3q325NmELajudTcMF3sYsv+ZJ66qmmmiRJHuZhXuEVT+vv5/5CX9qUW7iFZSyjjjpKKKGddpawxPN6bcfcBrQP/o+ut3nMYznLOcIRv3INGqc4xVa28gzPsIxlVFMddSRTfPkpSrboUrhs0cVfumxEqJTRT7pshAx6KriYpoKLaSq4mKaCi2kquJimgotpKriYpoKLaSq4mKaCi2kquJimgotpKriYpoKLaRoEGwllHDgNghXRGT3hUkY/6YweGfRUcDFNBRfTVHAxTQUX01RwMU0FF9NUcDFNBRfTVHAxTQUX01RwMU0FF9M0CLYvyjhwGgRL/AeYKmPR863gU5jCIQ6RJu1tQcgDTBMkmMQkDnHI+6JiGLJaDBkjNOCCz2Uu9dQzmcmkSLGXvd4WhjTANEGCBSzgVm6liipu4iaOc9zb4rgPWYX4ZyzWQbA11LCBDd0DTNtpZz3ruZZrc657iIf4hm9CGWB6FVdxJ3dSRhkVVACwkY2c5GRsMg5Y3DMW6yDYS7iE8Yzv3iVJkqSMMuYxL+e6MsoASDWk2NW0i/3sLzRCXtOZzjCGUdLjh0XTmJZ3Xc+MjzU95v0rfgRSDSmebnqaj/go6ih9K9ZBsK/xGu/zPitZyQIWkCDBAzwQq0Gwj/M4L/ESa1jDdKaTJMkKVnCMY57WF8uQ1VJKo44QWwPaB2+llc1s5imeYjGLeYd3/Mrlm2aauZu7qaGG+cznBCeijiQh8uWnKK20soMdfjxVYJq73mSQcV3X8w1qXTLXFYjhze26RZ0j3IyNNLozmBHrjEHdvHRW/1QvpqngYpoKLqap4GKaCi6mqeBimgpepIYylNGMBqCaaqqoijhRPOnyyaHyL+MWtjCNaZRSSieddNDBEpbQSecAn7kYtmOGLp9sWCON3WV2cDjAAR/KbY8KXqR2s5sOOgDooIMneTLiRPGkghepDjrYznbSpNnPfj7l06gjxVJ052TKgO1mN7XUso1tUUeJLR1khkoZ/aSDTBn0VHAxTYNgI6GMA6dBsCI6yAxXJmM/NnnonO7NF+ftmKGDTBn0VHAxTQUX01RwMU0FF9NUcDFNBRfTVHAxTQUX01RwMU0FF9NUcDFNBRfTwj0nMybDQfOK+5BVYOKWiRw9efSc+w+sOcDMMTMjSNSHscBPgHFAOdAGHAf2QVgjhXTScS5FMGR10ZRF1FTVdL9fXVEdYZoeLgV+RWYfoQU4CJSRKf10VPBY6OeQ1VGM4mquZg97aKMtsFg9rZq1irqpdZ4ff/LNk3zX/B0XLr2QkmRAe6hDgEVkyv0esAu65wM7wKhgXrYv0RQ84uGgnvVzyOp85rOWtaxiFQ00sJOdgRd924FtvPrpq93vb/nFlpyP/+zBzzjxlxMcvucwkx+aHEzRx0HXWFJ4Dc4afu0S6olh0RQ84uGgnvXK2binMe+STjqpoILlLGcZy9jAhkCnz71w8IWz3q/7pbev5qe/OM3B+oMc/u1h5rw9h9LRPo4iHNrj7990/flzMvvjWRv9e7lcoil4xMNBvapuqCbVlOqeQ3mEIzkfP4lJ3YNx06RppZVTnAo04/Zx27n0D5eeueOy3I9v+6DrO4oDpKFiagVOqc+np/U8VhkBnAA+A/4J/Njfl8pH++A5tNBCPfWeH38917OOdXzO5zzBE7zBGwGmy6i8spLLb7nc8+Pfu/49Wl9opfKaSmp+X8Pw2cP9D/U5mZ+YVABXAX8mc5B5ChW8mO1hD0c5GsuBuFlT/jiF0xtPM3xWAMXO6gB2AzeQOY65CPgXMDK4lzwfFdxH7bTHutwAZReXUXZxWfAv9D6Zr9jzyRx0ziKz63II+DD4l8/SZSNCpctG+EmXjZBBTwUX01RwMU0FF9NUcDFNBRfTVHAxTQUX01RwMU0FF9NUcDFNBRfTVHAxTQUX01RwMa2fvw/u/IfM1ULiahTw76hD5KGM/pjgum7ei8D094yej13XnVNgoMA5jrMvzvlAGcOmXRQxTQUX0/pb8D8FksI/cc8Hyhiqfh1kihQb7aKIaSq4mKaCi2kquJimgotp/we9ZNx2ZyCFRgAAAABJRU5ErkJggg==\n",
+      "text/plain": [
+       "<Figure size 216x216 with 1 Axes>"
+      ]
+     },
+     "metadata": {},
+     "output_type": "display_data"
+    },
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "after iteration 1\n",
+      "iter    0   |   diff: 0.90000   |   V(start): 0.000 \n"
+     ]
+    },
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAALgAAAC4CAYAAABQMybHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvDW2N/gAAC7pJREFUeJzt3X1sFHUex/H3dLfda7Fsi+WxFnqgiE8nzxLQXDSKZwAl6N0BGrwcEWtiDBdz4eTwAm6M5yP+caeHwcgZY0vUoAl6Ph3VqMFEFBX1CkI5UChQSxGhXFvauT+229J2uzvdzu7M/vi8mo3d7c7up+OH7Uy7M1/Ltm1ETJXjdQCRdFLBxWgquBhNBRejqeBiNBVcjKaCi9FUcDGaCi5GCya7g2VZy4Bl0WuDpsCENEcSceJTbNu2kt3L6s+f6i1rqg2fDihW+sS+j6Tfs4eU0U1OCq5NFDGaCi5GU8HFaCq4GE0FF6Op4GI0FVyMpoKL0VRwMZoKLkZTwcVoKrgYTQUXo6ngYrSk7wdPi2JgNjAaCAFNwBHgdaDRk0TdLQeK4tz+D+BQhrP0xe8ZfZLPm4L/FhgB1AINwGBgDFCIPwoes5PueU56FSQBv2f0ON+AC25hMYtZLGYxa1nLt3ybeIF8ouU+BTx/xu0B0rbBlEce85jH1VzNClZw0ula3g7UpCdTT8UUcxu3MYQhrGGN8wUzmLGccpaxjC/4go1sdLZQBvPFk3LBY8WuoIJiigkSZAxjkhe8ueOSD1QAe4F9wB6gNdU08eWRx43cyBKWECRIgADncI7zgk8Cys+4/qa7+aCr2HOYg4VFM839e4AMZIwVezKTySWXAAHnBc9AvkRSPmTtZm7mbu5O6UmrL6nm8XmPc/JnZxTtBPAicDClhyTeoVYRIsxkJjn9/NGwcPlCDhcd7v2F1almi+md8RVeIUyYAIF+PVKmMg5nOFVU0U57v9Zj+vJ1cXLIWsqv4O/wDiWUMJ/5WB0r42Ve5kM+TL7w11C6s5TdY3bTPqYdJgPnAL8EKlNN1Ns61tFOO1dwBQEC2NhEiFBPfcLlGmgAYETVCA7VpHePKEKEu7iLMsrIJ59WWrmHe5IuF8tYXFVMY036dlzqqechHuIO7qCg42MPe3iMxxzlK60qpammiUavdq5s23Z8gSk20X/inZfBDLbv5E77Dd6wp8T5eq9LDjaje9w2A5vV2NyeZNmEF7vj0vtrZZTZa1hjv87rdhFFyR9reUeeCQPJ07+ME5lor2OdvYENzh4rwxlzyLFnM9t+iZfse7nXw3xdFyedde2o+hxyaKc9+YPkASuBeqCO6Hb3RUAB8G/gA8dxeoh9H33/1HKcMfYrripc3kHK/oze5+uS1k2Unhx90wCnga1EdzwuAHKB48AnwEdupYnPcUYP+T2j3/P1pPOiZJQyuknnRZGzngouRlPBxWgquBhNBRejqeBiNBVcjKaCi9FUcDGaCi5GU8HFaCq4GE0FF6Op4GK0FN4P7vzttd7wez5QRjc4eztv0ldwy7KWWZa1zbKsbSQ5llHEb3TAQ0Ypo5t0wIOc9VRwMZoKLkZTwcVoKrgYTQUXo6ngYjQVXIymgovRVHAxmgouRlPBxWgquBgt82MEfTI/sU/xTtxeDvwO+B/wV09S9ab16Ig3czLB8/mJxtB6TMi1ggcJcprTzhfweH6iMbQeExpwwWNzHucyl1Ws4hM+cbagx/MTkzoz32APcySj9ZhQygUPE2YJS5jDHABsbKYxjRZaEi73Dd/QSitc2OMLfvsf0zOfX2k9JpRywa/hGhawoNttv+74SGQhCznMYSJVEbbUbKGa6lQjpFe8nSMfilRFWF+znn3s8zpKfB6vx5QLvolN1FFHBRUMZShBgjzKo7zLu46Wv5/7U31q6aGIIv8W3GMD2gb/uONjBjNYzGL2stetXCKucOW3KLGii/jOQEd5++fS95hs/1zcz1hNtX05l/s6Y7ouTjqrP9WL0VRwMZoKLkZTwcVoKrgYTQUXo6ngYjSdPjmj3Mu4ilVMZzqFFNJGGwc4wFKW9u8ty3Flw3qM0umTDVZPPSFCAAQIcLrjQ7pTwbNUJZW00w7AKU7xNE97nMifVPAsdZzjvMqrtNFGHXVsY5vXkXxJBc9ilVRyjGM8xVNeR/Et7WRmlDK6STuZctZTwcVoGgTrCWUcOA2CFdFOZmZFMx48WOdxjr6NGjWy4zM/r8co7WTKWU8FF6Op4GI0FVyMpoKL0VRwMZoKLkZTwcVoKrgYTQUXo6ngYjQVXIymgovRNAg2nizIOP3F6Xx/4vtet7+94G0uLbnUg0Q9aBAs/h9gmgUZrx19LeWDyzuvn5t/rndhfMi1go9nPLvZ3XmujqSyYYBpFmRcNGERN5Tf4HUM3xpwwacxjQoqGMtYIkTYwhZnC/p9gClkRcbKmkq2Htzaef2BmQ94mCaObB0EO45xrGQlIxlJPvk008xylnMd1yVc7mEe5hjH/D/AFLIi47v7u49t9F3Bs3UQ7Hmcx2hGd26SBAkSIsQMZiRcLnY+vUhVhE01m/iMz1KNkHaRqgiNNY08wRNeR+lTpCrC4kcXkz8l3+so8WXrINj3eZ+v+IolLOF6ridAgAd50LhBsEMZ6nWEpOxmvx8B750BbYM30MBa1vI8zzOPeXzO527lEnGFK79FaaCBDWxw46FEXKXTRiRQTTUf8zH3cZ9Lj+j+aSN2jtpJ2ctlFMwscOXxdNoIkSyigovRVHAxmgouRlPBxWgquBhNBY8jl1yGMxyAMGGGMczjRL21HW+j9btWAFrrWjldrxGC8ajgcSxiES/wAgAXcREb2cj5nO9xqu4O3H6A2qtqATj0h0PUzqjFbtGf7HtSweP4iI+6DVVtpJG97PUwUW+FNxViBTv+ztEOBVcWYOX5/48zmaaCx7GHPexgB2200UQT61lPG21ex+omvCiMFYoW2sqzGLrS/28K84IK3odneIZ22mmmmbd4y+s4veSEcij5YwnkQMFVBYQuDHkdyZe8OybT53azm9d4jS/50nev3jHhRWGaPmiiZEWJ11F8S2+2yijN6HGT3mwlZz0VXIymQbAe6NoM8DO/r0cNghUxbyczG3bg+rHKM87qfGHUTqaI76ngYjQVXIymgovRVHAxmgouRlPBxWgquBhNBRejqeBiNBVcjKaCi9FUcDFaZo/J9Mlw0GR8P2QVKH+ynH0/7ut1+/Y7tzNxxEQPEsVRClwJlAH5QBNwBNgG/CczEXTQcQLZMGR17vi5jCse13l9aIFPTh9xMXAL0W2EemAXECJa+stQwf2gv0NWW+ta+WnzT4QXhgkUBtKYrMvSSUuZP2G+4/v/uPVHTu05xbCFw8gJpmkLNReYS7TcO4BN0Dkf2AIyeBIAbwru8XBQp/o7ZPXEWyeof6CeHx75gSF3DaH4juK0F/3Z7c/y3n/f67z+5K+eTHj//Q/t5+i/jlK7opaxD49NT9HLgNhElfeh2/Brm4weGOZNwT0eDupUzyGrt95ya/KFAmCftDn6t6Mc/ftRSv9ZyqArB6UpIWzetbnb9fk3OHs1bznYwq6KXdT+qZapn04lb3iee6HO/HaPdfz3WqLb4zGr3Xu6RLwpuMfDQZ1ad8k6Lotc1jWHMsk/zJadLdEfy21AAILDggSGpPcV/Lmy57j4iYu7brgk8f2bvm6KfmIRPafhhDSc0/DkGZ8PBo4C+4EvgV+4+1TJaBs8gWBpkPI3yx3fv3FDI0f+fITcn+cy7C/DGDR7EJaV3mMbi2YWMf330x3ff8dNO2jY3EDR1UWMe2QchZML3Q/1HdHfmBQAVwGvEd3JPI4Kns3CvwkTuiBE/sz8tBc7VeOfHk/L6hYKJ6Wh2DGtwBvAAqL7WyOB74Fw+p6yLyq4i3IKciiY5c68ynQJjQoRGpWBE3V+RfQVexbRnc5JRDdddgPfpP/pY3TaiAzSaSPcpdNGyFlPBRejqeBiNBVcjKaCi9FUcDGaCi5GU8HFaCq4GE0FF6Op4GI0FVyMpoKL0VRwMZoKLkbr5/vBrZ+AnemLM2AlwA9eh0hCGd0xxrbtpCeB6e8RPTtt256aYqC0syxrm5/zgTJmmjZRxGgquBitvwV/Ji0p3OP3fKCMGdWvnUyRbKNNFDGaCi5GU8HFaCq4GE0FF6P9H/Z1DLrmkiWrAAAAAElFTkSuQmCC\n",
+      "text/plain": [
+       "<Figure size 216x216 with 1 Axes>"
+      ]
+     },
+     "metadata": {},
+     "output_type": "display_data"
+    },
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "after iteration 2\n",
+      "iter    0   |   diff: 0.81000   |   V(start): 0.000 \n"
+     ]
+    },
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAALgAAAC4CAYAAABQMybHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvDW2N/gAADG1JREFUeJzt3X9s1PUdx/Hn93rt0RYolVKQiq02AuPHtFiRgLpBiBFFaVA2QMPmD5AlLpMtDrPpIHYJm+D0D5dZweiWKDUh0SVsUyTgnAszYDrG0IJQx88C5UctUKCl990f15b+uPau1/ve9/v98Ho0DXfHfe/e/fbFl8/37j6ft2XbNiKmCrhdgIiTFHAxmgIuRlPAxWgKuBhNARejKeBiNAVcjKaAi9GCse5gWdYSYEnkWvatMNbhkkTi8Tm2bVux7mX15a16yyq14fN+leWctp8j5s/sItWYTPEEXEMUMZoCLkZTwMVoCrgYTQEXoyngYjQFXIymgIvRFHAxmgIuRlPAxWgKuBhNARejKeBitJifB3dELnA3cD0QAhqBE8BfgDOuVNTZ08CQKLe/BhxLcS098XqNHqnPnYB/HxgB1ACngMFAITAIbwS8zR4613PerUJ64fUaXa6v3wG3sJjGNBaykJd5ma/4qvcNMomE+wLwpw63p+HYgCmDDO7nfqYzneUs53y8e7kKqHampqRJYY1FFLGEJexkJ+/ybnwbubwPEw54W7CXspRccgkSpJDC2AG/1PqdCSwFvgYOAPuB5kSriS6DDB7gARaxiCBB0khjIAPjD3gJUNTh+gfJrS8pUlBjW7AnMYl00kkjLf6Au7wPE56y9iAP8hRPJfSkW8dv5aX7X+L8gA5BOwe8AxxN6CGJNtWqnHKmMpVAH/9rmP/0fI4POd79L1YmWlubJE4H62mMu7K/D9y5xuEMp5JKwoT7tB+d24dXxDNlLeEj+Ed8RB55lFGG1bozNrCBT/k09sa7oWBPAfsK9xEuDMMkYCDwHWB9ohV1V0EFYcLczu2kkYaNTTnl1FHX63anOAXAiMoRHKv2whlbz8ory9lQvYGd7HTk8euoYxWrWMxislq/9rOfNazpdbu2fVhQWUBjdSNnXDq5SjjgDTRQQQXrWc8CFjCHOVRRRXWsAVcAuA44SGRYsp/Iqyj3ABmJVhPdYQ6zghWMYhRP8ASllLKLXdRTH9f2xzzxcoS7woTZxCY2s5mZzGQxi/mSL2P/nlsd4YjDFfau3yeZbUFfy1rChON7xseAOqCWyLj7W61/V9PfaqI7xCFWsIIAgfhqlG46Bt1P+zBpLxPG/UNfBrYROfG4CUgHGoDtwD+TVU10fvrFeJXv9qFt23F/w602kbMQD37brd9u15HaGrey1b6Zmz1do1Pf8WRWb9WL0RRwMZoCLkZTwMVoCrgYTQEXo7nzcVnpt3nMo5RSAJaxjN3sZg1rsLFdrsxbFHCfmsCE9oAXUshgBhMgQAstLlfmLRqi+NQ61tHc+vniRhpZxzqFOwoF3KcOcYjP+IwwYS5xiQ/50O2SPEkB97F1rGv/U0fv6NSjJ6WSX2M++ZzkZBI/BOWH/Rjh6IQH8YYTnHC7BE/TEEWMlsAR3Ouvs3q9PlCNyRDfECrmEdyyrCWWZe2wLGsHMeYyiniNTjJTKlJjVdW/Xa6jZyUlt7Re8vJ+jFAjWLnqKeBiNAVcjKaAi9EUcDGaAi5GU8DFaAq4GE0BF6Mp4GI0BVyMpoCL0RRwMVrqZ/R4pH9ij9rqq+RKd7Ai4IfAReA3rlTVzb2b7qX2Qm232yu/W8mYnDEuVNSFR/aje1PWvN7f0SfuGn4X12Vf1349NyPXxWq8J2kBDxLkMpfj38APPSh9oKywjOnXTne7DM/qd8BzyeURHmE2s3mO59jO9vg29HoPyo71DXaxjhjeP/A+O07uaL/+zMRnXKwmCpf3Y8IBzyGHRSziPu4DwMbmNm6jiaZet/uCLyIrMnUdJnot4B4Yxsbjk+OfdLruuYC7vB8TDvgMZjCXuZ1um9f61Zv5zOc4xymvLGdL9Ra2sjXREpwV7eTIg8ory5n161mkFae5XUp0Lu/HhAP+Hu9RSy1LWcowhhEkyGpWs5nNcW3/PM8n+tTSRfhMmDQ8GnCX9WsM/q/WrylMYSEL+Zqvk1WXSFIk5VWUtqCLeI2WjUip5C8bUV9ST/babNJL05PyeFo2QsRHFHAxmgIuRlPAxWgKuBhNARejKeBiNAXcp84/e576u+ojl588T0NZA3az1xetTz0F3KcC+YHIzBiAMJCOOi5FoYD7VOjREO2fr8qEzJ9mYlnef/cx1RRwnwrkBgjNC0EAAgUBglN0+I5GAfex0KMhrFyLzJ/p6N0T/bP3sUBugJzNOW6X4Wk6govRFHAxWgKfB98R+44ijrOS83lwNYIVPzNuRo8fmqwePdp9yTWvGDny2tZL3n9VRjN65KqngIvRFHAxmgIuRlPAxWgKuBhNARejKeBiNAVcjKaAi9EUcDGaAi5GU8DFaGoEG4Xnm6wCk9+ZzOFzh7vdvmnuJibkTXChoi7UCBbPN4L1Q5PVmdfPpGhwUfv1oZlD3SvGg9wLeAKNYEczmn3sI0zYkZK68kOT1QVjFzCraJbbZXiWewHvYyPYG7iBCiqoo47XeZ0tbHE86J5vsgqsr17PtqPb2q+/MPUFF6uJwq+NYPuty1B21Qerer37cIYTJswwhrGMZSxhCatZHX9n5QR4vskqsPlg57aNngu4XxvB9tfQyqFsqN6Q0LYZrV/jGOdowMsry5kxfgZZz2U59hz9VV5ZzsLVC8m8NdPtUqLzayPY/jrFKaYT//i2mGJe4zVaaGE721nLWg5y0MEKI8LHUjPe7w/7klaV7YlvVrY6whHe5m22sCUlwRYz+CbgF7nIW7zldhniM1o2ohf1JfUEpwUZ+OrApDyeE8tG7Bm5h1EbRpE1NTnnCVo2QsRHFHAxmgIuRlPAxWgKuBhNARejKeBR2JdsWo62RC7X24RrvfduZktDC82HmgForm3mct1llyvyJgU8iotvXuTsA2cBaNndQsO9DVyu9laAjvzgCDV31gBwbNkxaqbUYDfpLfuuFPAo0qend3qP18q1SCtO63kDFwyaMwgr2Po+Rxiy7sjCyvD+mzOppoBHERwTJFgSjOydTBjw4wFY6d4KT86CHKxQpCYrw2LYL4a5XJE3KeA9GPCTARAAa4BFxuwMt8vpJhAKkPdMHgQg684sQmNCbpfkSb75sFWqBccGyZiXQXBS0HNH7zY5C3Jo/Ecjecvz3C7FsxTwXmT93LsTHSByFC94o8DtMjxNQxQxmgIuRlMjWPEpNYIVMW9Gjx+arPZhl6ec1X5M9OYrRx1pRo9c9RRwMZoCLkZTwMVoCrgYTQEXoyngYjQFXIymgIvRFHAxmgIuRlPAxWgKuBgttVPWPNIcNBbPN1kFil4p4sA3B7rdXvVkFbeMuMWFiqIoAO4ARgGZQCNwgsiUgi9TU4LmZPbCD01WZ4+eTXFucfv1YVkeWT5iHPAQkTFCHbAXCBEJ/UQUcC/oa5PV5tpmzm48S878HNIGpWahoMdLHqdsbFnc9/9m2zdc2H+B/Pn5BIIOjVDTgdlEwr0LeA/aW5paQAoXAXAn4C43B41XX5usnvvwHHUv1HHyxZNc86NryF2c63jQ36h6g4//93H79VfueaXX+x9cdZDTfztNzfIabvztjc4EfRTQtiDB36FTv16blE4McyfgLjcHjVfXJqsPP/Rw7I3SwD5vc/rV05z+/WkK/lhA9h3ZDlUIG/du7HS9bFZ8R/Omo03sXbqXmmdrKP28lIzhSVzcqOOPW9/650wi4/E2K5P3dL1xJ+AuNweNV8X4CiaWT7zShzLGP8ymPU2R/5ZbgDQI5gdJu8bZI/ibo95k3O/GXblhfO/3b9zdGLlgEVnTcKwDaxqe73B5MHAaOAj8B/h2cp8qFo3BexEsCFL0QVHc9z/z1hlO/PIE6Tekk/+rfLLvzsaynJ3bOGTqECY/Njnu+++as4tTG08xZPoQil8sZtCkQckv6hCRV0yygDuBPxM5yWxAAfeznO/lELopRObUTMeDnajRfxhN08omBpU4EOw2zcBfgblEzreuBQ4DOc49ZU8U8CQKZAXImubt5d5CI0OERqZgoc7/EjliTyNy0llCZOiyD/jC+advo2UjUkjLRiSXlo2Qq54CLkZTwMVoCrgYTQEXoyngYjQFXIymgIvRFHAxmgIuRlPAxWgKuBhNARejKeBiNAVcjNbHz4NbZ4E9zpXTb3nASbeLiEE1JkehbdsxF4Hp64yePbZtlyZYkOMsy9rh5fpANaaahihiNAVcjNbXgL/uSBXJ4/X6QDWmVJ9OMkX8RkMUMZoCLkZTwMVoCrgYTQEXo/0fCP8/6OLrIWkAAAAASUVORK5CYII=\n",
+      "text/plain": [
+       "<Figure size 216x216 with 1 Axes>"
+      ]
+     },
+     "metadata": {},
+     "output_type": "display_data"
+    },
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "after iteration 3\n",
+      "iter    0   |   diff: 0.72900   |   V(start): 0.000 \n"
+     ]
+    },
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAALgAAAC4CAYAAABQMybHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvDW2N/gAADN1JREFUeJzt3X1wFPUdx/H3Xi65PBRDJERNFIJRRIVqAB9G1IpCBhytjA8t4DAWHVBm6NTSsTptpzKmM7RWq+PUQWvVKjMSH2bqUxUjM1qVYbRQKlQFlVRReQgkYBCUJHfbPzYJIbnkLsnt/vZ+fF6Ow+2xy35v+bDZ27vf7+u4rouIrSKmCxDxkwIuVlPAxWoKuFhNARerKeBiNQVcrKaAi9UUcLFaNNUKjuMsBBZ6S0WTYJzPJYmkYz2u6zqp1nIG8lG940x2Yf2QyvJP5+tI+ZoN8mqsr3/dcB19q6mZ3vEozMfRk07AdYkiVlPAxWoKuFhNARerKeBiNQVcrKaAi9UUcLGaAi5WU8DFagq4WE0BF6sp4GI1BVyslvL74L4oAWqAUUAMOAg0Av8A9hqp6Ei3AsOTPP8QsDPgWvowb/08dh3a1ev55Wctp6qoykBFPYTkGJoJ+I+B44EGoAk4BhgNDCMcAe+0hSPrOWCqkL6dV3Ie5fnlXcvF0WKD1SRh+BgOOeAODlOYwlzmch/38Qmf9L9BAV64vwWe7PZ8DuG7YNoAbE5/9fGMZxGLeIIneI/3fCuruxllM5gyYkog+6qkkoUs5H3e52meTm+jAR7DTBt0wDuDfQu3UEIJUaKMZnTqgB/q+L8AuAX4H/A5sBVoG2w1PqkGKrstr+p/9SqqGMtY7uROGmlkOct9D/qqxlVsbNnYtbxozKKM76Mz2BOZSC655JCTfsAHeAwzbdBD1q7hGhazeFA7fePMN7j3yns5kN/t59U3wFPA9kH9kWR0yFof149vLH0j5aYJEkS6/ShaxjLqqe9YytyQtb6uwesvqE+ydvp6Dlk7juOoo67X60pl9q2z2TW8d30sHVJ5R0hnyNqgz+Cv8zqllDKLWTgdB+M5nuMd3km98QdQsaWCT0d/SmJ0AiYC3wN+AKwcbEWZF62LcsrmU7qWF9H/2XE607mSK2mlFReXZ3mWNazxtcbaulrOv+l83LP8mQZ7N7tZxjIWsIDCjv+2spV7uKff7ZpoAqCiroKDmw+y19Cbq0EHvIUWHuZhVrKSOczhKq5iAxvYnOqCKwKcCGzDuyzZincXZQaQN9hq/NFOe+rX081IRjKTmTzLszzDMxwI47vSAUqQoJ56VrOaaUxjAQv4iI/SPi5f8ZXPFfZvyG8yO4P+CI+QIJHeHm8EdgM78K67T+/4vYahVmPW27zNGtakdxyyTPegZ9Pry9htwrRfdDuwFu+Nx6lALtAC/At8/mkeiGz6yx+MbHt9wd8HTwCvBb7XgbnfdAGprZi0AoDcpbm00264miRCcgzDdudZJKMUcLGaAi5WU8DFagq4WE0BF6uZ+bqsDFnkuQjOeu8rEjkP5JA4PUFiSUKnrB4U8CzlfODg/NsLuPOFQ6QlQiKhgPekw5Gl4vPj3qfAgJvvEr8xrtNVEgp4thoF7jkuruNCDNzp/nybMNsp4FksPj/u/aqzd590WLLZKGhf0Q4jTBcSXgp4tiszXUC46RJFrDaIMZnrfCxHJF1OZtoIOo6z0HGcdY7jrPOG4YhkDzWCDZRX44YN/zFcR9+qq8/ueBTm4+hRI1g56ingYjUFXKymgIvVFHCxmgIuVlPAxWoKuFhNARerKeBiNQVcrKaAi9UUcLFa8CN6QtI/sU+d9dVxuDtYJfAT4Dvg90aq6uXy+svZ8e2OXs/XXVLHacWnGaioh5AcR3ND1rKgB2U2uPi4izmx6MSu5ZK8EoPVhI+5gBvun2iLWaNnMfWEqabLCC1zATfcPzGl7vUdY7COFJ7//HnW7Tk8jPC2CbcZrCYJw8fRXMB7XiaGLeAhuIxNx1u73jpiOXQBN3wcjQW8pq6GGZtnsIQlpkroX7I3RyFUW1fLzN/NJKcqx3QpyRk+jsZuE45lLNVUm9q9VRJ7s6vzWZB0H1yspoCL1YxNG/EYjzGGMUwlU7e4js5pI/ZV76PokSJyJ+dm5M/TtBEiWUQBF6sp4GI1BVyspoCL1RRwsZoCLlYLPOCnciov8AJjGAPAi7zIZVwWdBlZ78AdB9h38T7v8c0HaJnVgtumTms9BR7wZpopoKBrOY88GmkMuoysFymLeCNjABJ4PTPVcamXwAPeRBOv8iqttJIgwVa2solNQZeR9WLzY9D5BcICKFhSgOOE/9PHoBm5Bn+SJ3FxaaWVh3jIRAlZL1ISIXZdDCIQqYgQPV+n72SMBLyJJl7iJT7kQ529hyA2P4ZT4lDwC529+2Lsn/2DPGhq19aIlEQoXl1suoxQ021CsZoCLlZTI1jJUmoEKzLwM3h9/TIfyxm8mprpQHY0Wd2+vfeUa2FRXn5Cx6Pw35XRiB456ingYjUFXKymgIvVFHCxmgIuVlPAxWoKuFhNARerKeBiNQVcrKaAi9UUcLFa4EPW5q2fx65Du3o9v/ys5VQVVQVdTlKhb7IKnPvUuXz5zZe9nq+/up7xpeMNVNTD0d4I9ryS8yjPL+9aLo6Gb2xhNjRZnTZqGpXHVHYtjygYYa6YEDIW8BllM5gyYkr6G7jAJ0AVh+cD8Vk2NFmdM24OMytnmi4jtIwFfFXjKja2bOxaXjRmUf8bfAa5i3NxR7jEb4rjTnV9D3rom6wCKzevZO32tV3Ld11wl8FqkjhaG8G+u/fdI5YX/3Vxv+s7jQ6u4+I0OeQ8kAOPQnxJHPcc/+bjC32TVWD1ttVHLIcu4EdrI9g7S+/kksWXDG7jVqANnI8cXwNeW1fLpWdeSuFvCn3bx1DV1tUy949zKZhUkHplEww3gjU339cIaKtvS3/9rRBdHIUccCd5lymM8q+8Tomd4W+y6h7SrLJ9yZ4J7cohMTtBYmoikGCLHbIn4AWQuCH8Z1MJl8ADvmLSiqB3OWCv1LwCwL6l+2AAdzKD9N7c9wDYsnSL4Ur6cH+S5z4DlgZbhj6qF6sp4GI1BVyspoCL1RRwsZoCLlZTwJNwD7nEt8e9x/tcEjvCd/893hKn7Qvvk+C2HW207243XFE4KeBJfPf4d+z/4X4A4h/Eabm8hfbN4QrQVzd8RcNFDQDs/PlOGs5vwG3VR/Y9KeBJ5E7NPeIjMKfEIacqoC+hp2nYVcNwoh3TYyeg8MJCnLzwz+kdNAU8iehpUaLVUe/oFED+T/NxcsMVnuI5xTgxryYnz2Hkr0YariicFPA+5P8sHyLg5DvkXZFnupxeIrEIpbeVQgQKLyokdlrMdEmhlD1ftgpYdFyUvOvyiE6Mhu7s3al4TjEH3z5I6e2lpksJLQW8H4W/DO9AB/DO4hWPVpguI9R0iSJWU8DFamoEK1lKjWBFBnMGX+9jOUPhvY5saLI6gEMeOKfrnBjOO0fdqRGsHPUUcLGaAi5WU8DFagq4WE0BF6sp4GI1BVyspoCL1RRwsZoCLlZTwMVqCrhYLdghayFpDppK6JusApX3V/L515/3en7DzRs4+/izDVSURAVwIXASUAAcBBrxhhR8FEwJGpPZj2xosnrF2CuoKjncIXpkYUimjzgDuBbvGmE38DEQwwv9BBTwMBhok9W2HW3sf3k/xbOLyRkWzERBN1XfxKxxs9Je/+u1X/Pt1m8pm11GJOrTFWoucAVeuDcBfwc6Z79zgAAnATATcMPNQdM10Car37z2Dbvv2s2eu/dw7KJjKVlQ4nvQH93wKG9+9mbX8v0zkvUOOWzbsm00v9pMw+0NnPyHk/0J+klA54QE/+RwuMEblxLgwDAzATfcHDRdPZusXn/t9ak3ygH3gEvzn5tpfrCZiicqKLqwyKcK4eWPXz5iedbM9M7mrdtb+fiWj2m4o4HJ6yeTd1wGJzfq/nL3dfw6De96vNPSzO2uP2YCbrg5aLoePvNhJtROONyHMsU/zNYtrd6P5TiQA9GyKDnH+nsGf/ykxznjT2ccfuLM/tc/+MFB74GDN6fhOB/mNDzQ7fExQDOwDdgIfD+zu0pF1+D9iFZEqVxVmfb6e/+2l8ZfN5I7Jpey35ZRVFOE4/g7tnH4BcM598Zz015/01WbaHq5ieFTh1N1dxXDJg7LfFFf4N0xKQQuAl7Ae5PZggKezYp/VEzs1BgFFxT4HuzBGrt8LK1LWxlW7UOwO7UBrwBX473fOgH4Eij2b5d9UcAzKFIYoXBKuKd7i5XHiJUHMFHnf/HO2FPw3nRW4126fAp86P/uO2naiABp2ojM0rQRctRTwMVqCrhYTQEXqyngYjUFXKymgIvVFHCxmgIuVlPAxWoKuFhNARerKeBiNQVcrKaAi9UG+H1wZz+wxb9yhqwU2GO6iBRUY2aMdl035SQwAx3Rs8V13cmDLMh3juOsC3N9oBqDpksUsZoCLlYbaMD/4ksVmRP2+kA1BmpAbzJFso0uUcRqCrhYTQEXqyngYjUFXKz2f0FXYMPK0OcSAAAAAElFTkSuQmCC\n",
+      "text/plain": [
+       "<Figure size 216x216 with 1 Axes>"
+      ]
+     },
+     "metadata": {},
+     "output_type": "display_data"
+    },
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "after iteration 4\n",
+      "iter    0   |   diff: 0.65610   |   V(start): 0.000 \n"
+     ]
+    },
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAALgAAAC4CAYAAABQMybHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvDW2N/gAADVpJREFUeJzt3X9wF3V+x/Hnbr7ffPOD8E1IjBgUwuVUCmcVELSgCFdlgNo7xvFa0TpUaT2ZwbmrrXLFtpcxnVGvnY5zV4fROcfe0ZH8cTN37ViP45wOd9cbhytIB4onVqKCggQIMSE/v/l+t38sSQj5Jt98SXY/+/3weswwZJf9zr6zvPLJfve7+3k7nuchYivXdAEiQVLAxWoKuFhNARerKeBiNQVcrKaAi9UUcLGaAi5Wi+XawHGcx4DH/KXyxTAv4JJEcps27QidnZ1Oru2cfD6qd5xbPdg/qcKC438fO3c2G65jbBs2PADA7t0/N1zJ2FavvgeI9nEE2LZtGy0tLTkDrlMUsZoCLlZTwMVqCrhYTQEXqyngYjUFXKymgIvVFHCxmgIuVlPAxWoKuFhNARerKeBitZz3gweiClgNzAYSQDfQCvwHcM5IRSM8cfQJzgycGbX+uTnPUV9SH35BWTy8/2FO9Z0atX77zdtpKG8wUNFIUTmGZgL+x8BMoAU4C0wH5gAVRCLggxaVL6K2uHZoeXrRdIPVZHdb1W3UldQNLSdjSYPVjGb6GIYf8FL8cPcAP7xofRGRO2FamVzJkoolE94+/l6cin+t4Pz95+m/uR9y3o4/eWtq17C8ennwOwJix2NM2zmN/nn9dH+le0KvyfcYTrXwA9534U8p8DjwIfAxcBRIhV7NuPZ8vod3e94dWt5Yu3Hc7WPHYsQ/jFP5YiXpmjSdf9IZeNB3te7iYMfBoeXNczdP+T5ix2NMe30aicMJ//8ozYQDnu8xnGrhBzwD/DvE/jDGwMwBfzT/PeA88DpwIvSKxvRO1zvQNby89Rtbc77GczzcPhf3U5cZL8yg/fF2eu/qDazGvef2jlie6oC7p11qnq7Bw8O58JNacrCEmRtmjvu6om8WQeXoY2h/wAEOw0tHXqJ9Tjtb52yFRcA04C5gp5GKsnqy9kmWnV02tHy26ey425f8qoSy/ywj42bAga51XfQt6Qu0xqbmJm7fdDvezcFMg52pztD+eDsVzRU4PQ5un0vquhQdj3WM/7p0BoCn3adZfNViMpWZQOrLJfyAu8C1ED8WZ+nRpf6pSTewBigOvZrxxSD1xYmfN7ltLqW/KKVrXRfdf9CNV27B3Osu9N7VS+8dvZT8VwkVzRWkvpjKeVy8ox4MwMDMATIVZsINJgIeAx6FZ04/w/yT8/1zut+58G8toVczpfqW9tG6uNV/w2ybouGgR+1iwHjCD/gA8DbE6+PsvX4vxIEO4L+BX4dezdSzMdwXK7Dvz8ybzJ9BI43MZS6rWBV6Cbl8r+F7pkvIacfiHQDEG+MMMGC4mtGicgwL6JeNSP4UcLGaAi5WU8DFagq4WE0BF6uFHvAaanie55nLXABe4AUWsCDsMgqe+yOXor/2L0oXfbcI9x9d/xKsjBB6wJMkWcLw7ZOLWMTVXB12GQXPOezgvOPf/OQcd3D3KuDZhB7woxxlP/tJkwagjTb2sCfsMgpe+pG0/ykw4JV4pB9Nm7p1LtKMnIO/wiukSNFDDy/zMhkNPfmbDd4SD8/xIAHePRbc2BUAIwH/gA84xCE66NDoPQnpR/zfghq9x2bssDTSSIyYRu/JmA0DOwag2nQh0WUs4N1M7JEnyaE29yZXMl0HF6tdRhvBfQGWIzJRDp7nTb6NoOM4jzmOs89xnH1wempqEwlJ3iP4zp1/FWA5l2+wyWook5FcNv9YHzjwP4brGNvChbdc+CrKx9E3JSO4SCFTwMVqCrhYTQEXqyngYjUFXKymgIvVFHCxmgIuVlPAxWoKuFhNARerKeBitdCf6IlK/8QxfROoBJqB9y6sqwf+FOgFnjdS1Sjrdq/jZM/JUeubVzZzY/JGAxVdIiLH0dgja6b7J9pixdUruLb82qHlquIqg9VEj7GAm+6faIv1c9az6proNRGICmMBN90/MaeF+L9Swe/EHFE/+fgn7Dsz/BjhUzc9ZbCaLAwfR2MBN90/MacInMZOxC9P/XLEcuQCbvg4Ggv4tg+2seKdFZz72wg1p79YtjdHEdTU3MTav19LUUNEu0MZPo7GLhPGP4yTeDdhavdWyZzT5Elj0XVwsZoCLlYL/Rx8sH9i9fcjOqHei1nWfQQ0hltGLm+ufhOA9sZ2w5WMISLHUSO4WE0BF6sp4GI1BVyspoCL1RRwsZoCLlYLPeCxD2PU/lkt8U/8Hni1m2op+XVJ2GUUvK5vddG+wr8G3vX1LjrWd+Cl1GntUqEHPJPM4PQNT+vspBzS1emwyyh4bq3rPxkDfgPYOOq0lkX4AZ+RoeeuHryYh4dHak6K1LxU2GUUvMQjCRi8gbAUSp8sxXGiP2l92Iycg5+/77zfQKAYOh/qNFFCwXOrXBJfS4AL7iyX2O0avrMxEvDMjAzdv99N//X9Gr0nIfFIAqfKofQvNXqPxdiPfedGjdyT5Va5JN9Kmi4j0nSZUKymgIvV1AhWCpQawYrkP4Lv3v1cgOVcvtWr7wEKo8nqiROjp1yLirq6ay58Ff2rMmoEK1c8BVyspoCL1RRwsZoCLlZTwMVqCrhYTQEXqyngYjUFXKymgIvVFHCxmgIuVgv9kbWH9z/Mqb5To9Zvv3k7DeUNYZeTVeSbrAJLX1/KJ+c/GbV+9327+VLNlwxUdIkrvRHsbVW3UVdSN7ScjEXv2cJCaLJ69+y7qZ9eP7RcXRrRxgKGGAv4mto1LK9ePvEXeMD/AQ0MzwcSsEJosrph3gbW1q81XUZkGQv4rtZdHOw4OLS8ee7m8V/wEcS3xPGqPdKb0nirvMCDHvkmq8DO93by9om3h5afXfaswWqyuFIbwe49t3fE8pbvbxl3e6fVwXM8nLMORd8tglch/WQab0lw8/FFvskq8Naxt0YsRy7gV2oj2G/XfJuVW1Ze3ov7gRQ4v3UCDXhTcxNfXvBlyv6mLLB9TFZTcxMP/sODlC4uNV1KdoYbwZqb76saUrvzmNXqKMS2xKAIvMX+aQqzgytvUOaz6DdZ9fo0q+xYCmdCuzrIPJAhsyoTSrDFDoUT8FLIbIz+aCrREnrAdyzeEfYu8zaiyWoeVzLD9JsHfwPAkcYjhisZgxrBigRPARerKeBiNQVcrKaAi9UUcLGaAp6F1+eRPuG3NvTaPTIno3f9Pd2RJnXc/yQ4dTLFwOkBwxVFkwKeRe9rvXR+xe8hlD6cpmNdBwPvRStAn278lJY7WwD47C8+o+X2Frx+fWR/KQU8i/iq+IiPwJwqh6KGkG5Cn6CKr1bgxC5Mj52BsjvKcIqjP6d32BTwLGI3xogtjPlHpxRKnijBiUcrPMkNSZyEX5NT7HDVtqsMVxRNCvgYSr5RAi44JQ7F9xabLmcUN+FS81QNuFB2ZxmJGxOmS4qkwrnZKmSxeTGKv1ZMbFEscqP3oOSGJN2/6qZma43pUiJLAR9H2dPRfdAB/FF81quzTJcRaTpFEasp4GI1NYKVAqVGsCKXM4LvD7CcyfC/j0JosprHIQ+dMzQmRvPK0cXUCFaueAq4WE0BF6sp4GI1BVyspoCL1RRwsZoCLlZTwMVqCrhYTQEXqyngYjUFXKwW7iNrEWkOmkvkm6wC9S/W8/HnH49af+DrB7hl5i0GKspiFnAHcB1QCnQDrfiPFPw2nBL0TOY4CqHJ6r033EtD1XCH6KvKIjJ9xHzgfvxzhNPA+0ACP/Q3oYBHQb5NVlMnU3S+0UnygSRFFeFMFLRp4SbWz1s/4e0/f/tzeo72UPtALW4soDPUOHAvfrgPAT8GBme/c4AQJwEwE3DDzUEnKt8mq+d/dp7Tz57mzHfOMGPzDKr+vCrwoL964FX2fLRnaPnFNdl6hww79twx2n7aRsvWFr7wwheCCfp1wOCEBL9gONzgP5cS4oNhZgJuuDnoRF3aZPWh+x/K/aIi8Lo82v65jbaX2pj1g1mU31EeUIXwxvtvjFhev3Zio3n/iX7ef/x9Wr7Vwq37b6X46imc3Ojib7f9wt9345+PD2qcut2Nx0zADTcHnaiXF7zMTU03DfehzPGD2X+k3/+1nAaKIFYbo2hGsCP4a9e9xvx/mj+8YsH423cf7va/cPDnNJwXwJyGXRd9PR1oA44BB4Hfndpd5aJz8HHEZsWo31U/4e3P/cs5Wp9pJT43Tu3f1VK+uhzHCfbZxspllSx9dOmEtz/01UOcfeMslasqafhOAxWLKqa+qOP4V0zKgDuBf8N/k9mBAl7Ikn+UJHF9gtJlpYEH+3LdsP0G+hv7qVgYQLAHpYA3gfvw329dA3wCJIPb5VgU8CnklrmULY/2dG+JugSJuhAm6vxf/BF7Of6bzoX4py4fAO8Gv/tBmjYiRJo2Ympp2gi54ingYjUFXKymgIvVFHCxmgIuVlPAxWoKuFhNARerKeBiNQVcrKaAi9UUcLGaAi5WU8DFanneD+50AkeCK2fSaoAzpovIQTVOjTme5+WcBCbfJ3qOeJ5362UWFDjHcfZFuT5QjWHTKYpYTQEXq+Ub8FcCqWLqRL0+UI2hyutNpkih0SmKWE0BF6sp4GI1BVyspoCL1f4fN1WKxsZjRmUAAAAASUVORK5CYII=\n",
+      "text/plain": [
+       "<Figure size 216x216 with 1 Axes>"
+      ]
+     },
+     "metadata": {},
+     "output_type": "display_data"
+    },
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "after iteration 5\n",
+      "iter    0   |   diff: 0.59049   |   V(start): 0.590 \n"
+     ]
+    },
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAALgAAAC4CAYAAABQMybHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvDW2N/gAADcpJREFUeJzt3X1sXNWZx/HvuTPjGb+Mx46dKTgJOHVCXCgLwSSgBPJSIEpSRLMorRLYKEvT0rgKossu0M2+NMKrsm23K1R2FVGVsqtUxFLZbldCaZqlW9ouQqkCQWEhCRAn5JXYie343Z6Xu3/c2Mbx2OOxfe+5c/J8/vGc0R3N46ufj+/cufc8yrZthDCVpbsAIdwkARdGk4ALo0nAhdEk4MJoEnBhNAm4MJoEXBhNAi6MFsy2gVLqUeBRZ1RcB7UulyREdiUlR+ns7FTZtlO5fFWv1O32zp1fm1Jhbqmv3wrA7t2NmisZ28aNGwDYt++/NVcytlWr7gP8vR8Btm/fTlNTU9aAyyGKMJoEXBhNAi6MJgEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0aTgAujScCF0bJeD+6GlmQLv+j6BR8NfESf3UeJVUJVsIoN0Q3MDM7UUdIIjx17jAvJC6Oef/b6Z6mOVHtfUAab3trE+f7zo57fectOaoprNFQ0kl/2oZaAv3DpBc4kz7CgYAHxQJz2VDsfJj7kUvoSM9Ef8EG3Fd9GvCA+NC4NlGqsJrM7yu+gKlI1NI4FYxqrGU33PvQ84N3pbs4kz1CoCnm87HGUcq5ZT9gJbPy1TuKK2AoWRRdNePvQkRDRn0XpWt/FwC0DkPVy/KlbHV/N0oql7r8REDwVpGR3CQO1A/Q80DOh1+S6D6eb5wGPqAhhFabX7uW7rd9lQcEC5oXm8bnw5wirsNfljOv1S6/zfu/7Q+PN8c3jbh88GSR0PETZc2WkKlN0/lmn60Hf27yXQx2Hhsb1c+un/T2Cp4KUvFxC+L0wJIAUEw54rvtwunke8IAKsKl0Ey+3vczp5GlOJ0/zG35DqVVKfVk91aFqr0sa09vdb0P38Pjpx5/O+hpb2Vj9FtYZixnfm0H71nb6lve5VuP+tv0jxtMdcKvFovKpSmxs1OW/1MihCNdsvGbc1wW+FYCy0fvQ+IAD1EXqeOCnD3A4fJjfbv0tb/S+QUe6gz1de/hm+Td1lJTRE/EnWHJxydD4YsPFcbeP/CFC0f8UkbbSoKB7bTf9i/pdrbGhsYE7t9yJfYs7h3fpijTtW9uJNkZRvQqr3yIxJ0HHox3jvy6VBuAp6ynqZtaRLku7Ul82ngc8Zac4njjO3NRcFh9bTGlJKSWqhFe6XqHfdjcMOQtCYl5iwptbrRaFvyuke203PV/swS7212eKSbGgb3kffXf1EfnfCNHGKIl5iaz7xT5mQxKS1yRJR/WEGzQEPGEn+GHbD/n5V37O/FPz6evo452+dwCoDef3khT9i/tprmuGgO5KXBAYDno+fXviecBDKsQ9Rfdw4sIJ9s/fT19vH+WBcpZHlrOqaJXX5Uw/E8P9aXn2+2n5kLk+up65/zGX8LkwR3Ye8bqErJ6veV53CVntqtsFQGhHiCRJzdWM5pd9mEf/bITInQRcGE0CLowmARdGk4ALo0nAhdE8D3iwLcjs52cTPudcWDX7+dlEjkW8LiPvWa9YBP7aOSkd+FEA658s0PeFoW95HvBAV4Diw8VD4+KjxYRaQ16XkffUewr1tnPxkzqlsPZLwDPxPOD9c/rpru3GVs51Gsloks66Tq/LyHupR1JweV6wIzapr6Y0XTrnb1qOwVv+tAU7aJMuSNP8YLN8EpiM68BeZDsTRRjs+wy4sMsFWqLVP6efnnk9pIpTMntPQeqRlPNTZu8xadstZ79+FpVSMntPxXWQ3JWECt2F+Je2gKcL5RPRtIhn3+RqJvOnMFrObQThgIvlCDFRCtu2p95GUCn1qFLqgFLqALRMT21CeCTnGXz37r9ysZzJG2yy6sliJJPm7OuDB9/RXMfYFi689fIjP+9Hx7TM4ELkMwm4MJoEXBhNAi6MJgEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0bz/I4ev/RPHNO3gDKgERhc2bka+HOgD/hHLVWNsnbfWs71nhv1fOOKRhbEFmio6Ao+2Y/ablnT3T/RFMs+s4zZxbOHxuUF5Rqr8R9tAdfdP9EU665fx8prV+ouw7e0BVx3/8SsFuL8SwXw8T+XX378Sw5cGL6N8Mmbn9RYTQaa96O2gOvun5iVDw5jJ+L3538/Yuy7gGvej9oCvv2j7Sx7exltf9emq4TxZfpw5EMNjQ2s+Yc1BGp82h1K837UdpowdDxE+H1/te7OV+k2WWNmLHIeXBhNAi6M5vkx+GD/xIqf+HRBvecyPHcC2OFtGdnsWbUHgPYd7ZorGYNP9qPM4MJoEnBhNAm4MJoEXBhNAi6MJgEXRpOAC6N53wj2eJD41+KETjs98OJb4kTekEawuer+djfty5xz4N3f6KZjXQd2QjqtXcnzgKdjaVT/8LLOKqFIVaS8LiPvWXHLuTMGnAawIaTTWgbeB3xGmt7lvdhBGxubxPUJErUJr8vIe+FHwjB4AWEhFD5RiFL+X7Tea1qOwbse7HIaCBRA58PSJ3MyrHKL8JfDYIE1yyJ4p0zfmWgJeHpGmp57ehiYPyCz9xSEHwmjyhWFfymz91i0/dl3bpaZe6qscovYazHdZfianCYURpOAC6NJI1iRp6QRrBC5z+D79j3rYjmTt2rVfUB+NFk9e3b0kmt+UVV17eVH/j8rI41gxVVPAi6MJgEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0aTgAujScCF0Ty/ZW3TW5s4339+1PM7b9lJTXGN1+Vk5Psmq8Dilxdzuuv0qOf3PbiPz1d+XkNFV7jaG8HeUX4HVZGqoXEs6L97C/Ohyeq9191LdWn10Lii0KeNBTTRFvDV8dUsrVg68RfYwIdADcPrgbgsH5qsbqzdyJrqNbrL8C1tAd/bvJdDHYeGxvVz68d/wQkIbQthV9iktqSwV9quB933TVaB3Ud28+bZN4fGzyx5RmM1GVytjWD3t+0fMd72k23jbq+aFbayURcVgR8F4EVIPZHCXuTeeny+b7IKvHbytRFj3wX8am0E+53K77Bi24rJvXgASIA6rFwNeENjA1+46QsU/W2Ra+8xVQ2NDTz0g4corCvUXUpmmhvB6lvvqwIS+3JY1eoYBLcFIQB2nXOYwnXulTco/Yn/m6za/bKq7FjyZ0G7KkhvSJNemfYk2MIM+RPwQkhv9v9sKvzF84Dvqtvl9VvmbEST1RzOZHrpjw/9EYCjO45qrmQM0ghWCPdJwIXRJODCaBJwYTQJuDCaBFwYTQKegd1vkzrrtDa0223S5/x3/j3VkSJxyvkmOHEuQbIlqbkif5KAZ9D3Uh+dDzg9hFLvpehY20HyiL8CdGbzGZrubgLgk7/4hKY7m7AH5Cv7K0nAMwitDI34CkyVKwI1Hl2EPkHRL0VRwcvLY6eh6K4iVIH/1/T2mgQ8g+CCIMGFQWfvFELksQgq5K/wxDbGUGGnJlWgmLl9puaK/EkCPobI4xGwQEUUBfcX6C5nFCtsUflkJVhQdHcR4QVh3SX5Uv5cbOWxYG2Qgi8XELwt6LvZe1BsY4yeP/RQ+XSl7lJ8SwI+jqKn/HujAziz+KwXZ+kuw9fkEEUYTQIujCaNYEWekkawQkxmBn/LxXKmwvk98qHJag673HNqaE7055mjT5NGsOKqJwEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0aTgAujScCF0STgwmje3rLmk+ag2fi+ySpQ/Vw1H1/6eNTzB79xkFuvuVVDRRnMAu4C5gCFQA/QjHNLwWFvSpB7MseRD01W77/hfmrKhztEzyzyyfIRNwLrcY4RWoAPgDBO6G9GAu4HuTZZTZxL0PlqJ7ENMQJRbxYK2rJwC+tq1014+0tvXqL3WC/xDXGsoEtHqCHgfpxwvwv8JzC4+p0CPFwEQE/ANTcHnahcm6x2/bqLlmdauPD9C8yon0H518tdD/qLB1/k9ROvD42fW52pd8iwk8+epPVXrTQ93cRnv/dZd4I+BxhckOB3DIcbnPtSPLwxTE/ANTcHnagrm6w+vP7h7C8KgN1t0/ovrbT+ayuz/n0WxXcVu1QhvPrBqyPG69ZMbDYfODvAB1s/oOnbTdz+1u0UfGYaFzf69K/bfvnnvTjH44N2TN/bjUdPwDU3B52oF256gZsbbh7uQ5nlD3Pg6IDzbzkFBCAYDxKY4e4M/tKcl7jxn28cfuKm8bfvea/HeaBw1jSsdWFNw+5PPS4FWoGTwCHgT6b3rbKRY/BxBGcFqd5bPeHt2/6tjea/aSY0N0T87+MUrypGKXfvbSxbUsbiry6e8PbvfuldLr56kbKVZdR8v4bobdHpL+oUzhmTIuBu4L9wPmR2IAHPZ7GvxAjPD1O4pND1YE/WDTtvYGDHANGFLgR7UALYAzyI83nrWuA0EHPvLcciAZ9GVpFF0VJ/L/cWrgoTrvJgoc7/w5mxl+J86FyIc+jyEfC++28/SJaN8JAsGzG9ZNkIcdWTgAujScCF0STgwmgScGE0CbgwmgRcGE0CLowmARdGk4ALo0nAhdEk4MJoEnBhNAm4MJoEXBgtx+vBVSdw1L1ypqwSuKC7iCykxulxvW3bWReByfWOnqO2bd8+yYJcp5Q64Of6QGr0mhyiCKNJwIXRcg34j12pYvr4vT6QGj2V04dMIfKNHKIIo0nAhdEk4MJoEnBhNAm4MNr/A0vg0SO2dsmQAAAAAElFTkSuQmCC\n",
+      "text/plain": [
+       "<Figure size 216x216 with 1 Axes>"
+      ]
+     },
+     "metadata": {},
+     "output_type": "display_data"
+    },
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "after iteration 6\n",
+      "iter    0   |   diff: 0.00000   |   V(start): 0.590 \n",
+      "Terminated\n"
+     ]
+    },
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAALgAAAC4CAYAAABQMybHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvDW2N/gAADcpJREFUeJzt3X1sXNWZx/HvuTPjGb+Mx46dKTgJOHVCXCgLwSSgBPJSIEpSRLMorRLYKEvT0rgKossu0M2+NMKrsm23K1R2FVGVsqtUxFLZbldCaZqlW9ouQqkCQWEhCRAn5JXYie343Z6Xu3/c2Mbx2OOxfe+5c/J8/vGc0R3N46ufj+/cufc8yrZthDCVpbsAIdwkARdGk4ALo0nAhdEk4MJoEnBhNAm4MJoEXBhNAi6MFsy2gVLqUeBRZ1RcB7UulyREdiUlR+ns7FTZtlO5fFWv1O32zp1fm1Jhbqmv3wrA7t2NmisZ28aNGwDYt++/NVcytlWr7gP8vR8Btm/fTlNTU9aAyyGKMJoEXBhNAi6MJgEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0aTgAujScCF0bJeD+6GlmQLv+j6BR8NfESf3UeJVUJVsIoN0Q3MDM7UUdIIjx17jAvJC6Oef/b6Z6mOVHtfUAab3trE+f7zo57fectOaoprNFQ0kl/2oZaAv3DpBc4kz7CgYAHxQJz2VDsfJj7kUvoSM9Ef8EG3Fd9GvCA+NC4NlGqsJrM7yu+gKlI1NI4FYxqrGU33PvQ84N3pbs4kz1CoCnm87HGUcq5ZT9gJbPy1TuKK2AoWRRdNePvQkRDRn0XpWt/FwC0DkPVy/KlbHV/N0oql7r8REDwVpGR3CQO1A/Q80DOh1+S6D6eb5wGPqAhhFabX7uW7rd9lQcEC5oXm8bnw5wirsNfljOv1S6/zfu/7Q+PN8c3jbh88GSR0PETZc2WkKlN0/lmn60Hf27yXQx2Hhsb1c+un/T2Cp4KUvFxC+L0wJIAUEw54rvtwunke8IAKsKl0Ey+3vczp5GlOJ0/zG35DqVVKfVk91aFqr0sa09vdb0P38Pjpx5/O+hpb2Vj9FtYZixnfm0H71nb6lve5VuP+tv0jxtMdcKvFovKpSmxs1OW/1MihCNdsvGbc1wW+FYCy0fvQ+IAD1EXqeOCnD3A4fJjfbv0tb/S+QUe6gz1de/hm+Td1lJTRE/EnWHJxydD4YsPFcbeP/CFC0f8UkbbSoKB7bTf9i/pdrbGhsYE7t9yJfYs7h3fpijTtW9uJNkZRvQqr3yIxJ0HHox3jvy6VBuAp6ynqZtaRLku7Ul82ngc8Zac4njjO3NRcFh9bTGlJKSWqhFe6XqHfdjcMOQtCYl5iwptbrRaFvyuke203PV/swS7212eKSbGgb3kffXf1EfnfCNHGKIl5iaz7xT5mQxKS1yRJR/WEGzQEPGEn+GHbD/n5V37O/FPz6evo452+dwCoDef3khT9i/tprmuGgO5KXBAYDno+fXviecBDKsQ9Rfdw4sIJ9s/fT19vH+WBcpZHlrOqaJXX5Uw/E8P9aXn2+2n5kLk+up65/zGX8LkwR3Ye8bqErJ6veV53CVntqtsFQGhHiCRJzdWM5pd9mEf/bITInQRcGE0CLowmARdGk4ALo0nAhdE8D3iwLcjs52cTPudcWDX7+dlEjkW8LiPvWa9YBP7aOSkd+FEA658s0PeFoW95HvBAV4Diw8VD4+KjxYRaQ16XkffUewr1tnPxkzqlsPZLwDPxPOD9c/rpru3GVs51Gsloks66Tq/LyHupR1JweV6wIzapr6Y0XTrnb1qOwVv+tAU7aJMuSNP8YLN8EpiM68BeZDsTRRjs+wy4sMsFWqLVP6efnnk9pIpTMntPQeqRlPNTZu8xadstZ79+FpVSMntPxXWQ3JWECt2F+Je2gKcL5RPRtIhn3+RqJvOnMFrObQThgIvlCDFRCtu2p95GUCn1qFLqgFLqALRMT21CeCTnGXz37r9ysZzJG2yy6sliJJPm7OuDB9/RXMfYFi689fIjP+9Hx7TM4ELkMwm4MJoEXBhNAi6MJgEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0bz/I4ev/RPHNO3gDKgERhc2bka+HOgD/hHLVWNsnbfWs71nhv1fOOKRhbEFmio6Ao+2Y/ablnT3T/RFMs+s4zZxbOHxuUF5Rqr8R9tAdfdP9EU665fx8prV+ouw7e0BVx3/8SsFuL8SwXw8T+XX378Sw5cGL6N8Mmbn9RYTQaa96O2gOvun5iVDw5jJ+L3538/Yuy7gGvej9oCvv2j7Sx7exltf9emq4TxZfpw5EMNjQ2s+Yc1BGp82h1K837UdpowdDxE+H1/te7OV+k2WWNmLHIeXBhNAi6M5vkx+GD/xIqf+HRBvecyPHcC2OFtGdnsWbUHgPYd7ZorGYNP9qPM4MJoEnBhNAm4MJoEXBhNAi6MJgEXRpOAC6N53wj2eJD41+KETjs98OJb4kTekEawuer+djfty5xz4N3f6KZjXQd2QjqtXcnzgKdjaVT/8LLOKqFIVaS8LiPvWXHLuTMGnAawIaTTWgbeB3xGmt7lvdhBGxubxPUJErUJr8vIe+FHwjB4AWEhFD5RiFL+X7Tea1qOwbse7HIaCBRA58PSJ3MyrHKL8JfDYIE1yyJ4p0zfmWgJeHpGmp57ehiYPyCz9xSEHwmjyhWFfymz91i0/dl3bpaZe6qscovYazHdZfianCYURpOAC6NJI1iRp6QRrBC5z+D79j3rYjmTt2rVfUB+NFk9e3b0kmt+UVV17eVH/j8rI41gxVVPAi6MJgEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0aTgAujScCF0Ty/ZW3TW5s4339+1PM7b9lJTXGN1+Vk5Psmq8Dilxdzuuv0qOf3PbiPz1d+XkNFV7jaG8HeUX4HVZGqoXEs6L97C/Ohyeq9191LdWn10Lii0KeNBTTRFvDV8dUsrVg68RfYwIdADcPrgbgsH5qsbqzdyJrqNbrL8C1tAd/bvJdDHYeGxvVz68d/wQkIbQthV9iktqSwV9quB933TVaB3Ud28+bZN4fGzyx5RmM1GVytjWD3t+0fMd72k23jbq+aFbayURcVgR8F4EVIPZHCXuTeeny+b7IKvHbytRFj3wX8am0E+53K77Bi24rJvXgASIA6rFwNeENjA1+46QsU/W2Ra+8xVQ2NDTz0g4corCvUXUpmmhvB6lvvqwIS+3JY1eoYBLcFIQB2nXOYwnXulTco/Yn/m6za/bKq7FjyZ0G7KkhvSJNemfYk2MIM+RPwQkhv9v9sKvzF84Dvqtvl9VvmbEST1RzOZHrpjw/9EYCjO45qrmQM0ghWCPdJwIXRJODCaBJwYTQJuDCaBFwYTQKegd1vkzrrtDa0223S5/x3/j3VkSJxyvkmOHEuQbIlqbkif5KAZ9D3Uh+dDzg9hFLvpehY20HyiL8CdGbzGZrubgLgk7/4hKY7m7AH5Cv7K0nAMwitDI34CkyVKwI1Hl2EPkHRL0VRwcvLY6eh6K4iVIH/1/T2mgQ8g+CCIMGFQWfvFELksQgq5K/wxDbGUGGnJlWgmLl9puaK/EkCPobI4xGwQEUUBfcX6C5nFCtsUflkJVhQdHcR4QVh3SX5Uv5cbOWxYG2Qgi8XELwt6LvZe1BsY4yeP/RQ+XSl7lJ8SwI+jqKn/HujAziz+KwXZ+kuw9fkEEUYTQIujCaNYEWekkawQkxmBn/LxXKmwvk98qHJag673HNqaE7055mjT5NGsOKqJwEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0aTgAujScCF0STgwmje3rLmk+ag2fi+ySpQ/Vw1H1/6eNTzB79xkFuvuVVDRRnMAu4C5gCFQA/QjHNLwWFvSpB7MseRD01W77/hfmrKhztEzyzyyfIRNwLrcY4RWoAPgDBO6G9GAu4HuTZZTZxL0PlqJ7ENMQJRbxYK2rJwC+tq1014+0tvXqL3WC/xDXGsoEtHqCHgfpxwvwv8JzC4+p0CPFwEQE/ANTcHnahcm6x2/bqLlmdauPD9C8yon0H518tdD/qLB1/k9ROvD42fW52pd8iwk8+epPVXrTQ93cRnv/dZd4I+BxhckOB3DIcbnPtSPLwxTE/ANTcHnagrm6w+vP7h7C8KgN1t0/ovrbT+ayuz/n0WxXcVu1QhvPrBqyPG69ZMbDYfODvAB1s/oOnbTdz+1u0UfGYaFzf69K/bfvnnvTjH44N2TN/bjUdPwDU3B52oF256gZsbbh7uQ5nlD3Pg6IDzbzkFBCAYDxKY4e4M/tKcl7jxn28cfuKm8bfvea/HeaBw1jSsdWFNw+5PPS4FWoGTwCHgT6b3rbKRY/BxBGcFqd5bPeHt2/6tjea/aSY0N0T87+MUrypGKXfvbSxbUsbiry6e8PbvfuldLr56kbKVZdR8v4bobdHpL+oUzhmTIuBu4L9wPmR2IAHPZ7GvxAjPD1O4pND1YE/WDTtvYGDHANGFLgR7UALYAzyI83nrWuA0EHPvLcciAZ9GVpFF0VJ/L/cWrgoTrvJgoc7/w5mxl+J86FyIc+jyEfC++28/SJaN8JAsGzG9ZNkIcdWTgAujScCF0STgwmgScGE0CbgwmgRcGE0CLowmARdGk4ALo0nAhdEk4MJoEnBhNAm4MJoEXBgtx+vBVSdw1L1ypqwSuKC7iCykxulxvW3bWReByfWOnqO2bd8+yYJcp5Q64Of6QGr0mhyiCKNJwIXRcg34j12pYvr4vT6QGj2V04dMIfKNHKIIo0nAhdEk4MJoEnBhNAm4MNr/A0vg0SO2dsmQAAAAAElFTkSuQmCC\n",
+      "text/plain": [
+       "<Figure size 216x216 with 1 Axes>"
+      ]
+     },
+     "metadata": {},
+     "output_type": "display_data"
+    },
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "after iteration 7\n",
+      "iter    0   |   diff: 0.00000   |   V(start): 0.590 \n",
+      "Terminated\n"
+     ]
+    },
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAALgAAAC4CAYAAABQMybHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvDW2N/gAADcpJREFUeJzt3X1sXNWZx/HvuTPjGb+Mx46dKTgJOHVCXCgLwSSgBPJSIEpSRLMorRLYKEvT0rgKossu0M2+NMKrsm23K1R2FVGVsqtUxFLZbldCaZqlW9ouQqkCQWEhCRAn5JXYie343Z6Xu3/c2Mbx2OOxfe+5c/J8/vGc0R3N46ufj+/cufc8yrZthDCVpbsAIdwkARdGk4ALo0nAhdEk4MJoEnBhNAm4MJoEXBhNAi6MFsy2gVLqUeBRZ1RcB7UulyREdiUlR+ns7FTZtlO5fFWv1O32zp1fm1Jhbqmv3wrA7t2NmisZ28aNGwDYt++/NVcytlWr7gP8vR8Btm/fTlNTU9aAyyGKMJoEXBhNAi6MJgEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0aTgAujScCF0bJeD+6GlmQLv+j6BR8NfESf3UeJVUJVsIoN0Q3MDM7UUdIIjx17jAvJC6Oef/b6Z6mOVHtfUAab3trE+f7zo57fectOaoprNFQ0kl/2oZaAv3DpBc4kz7CgYAHxQJz2VDsfJj7kUvoSM9Ef8EG3Fd9GvCA+NC4NlGqsJrM7yu+gKlI1NI4FYxqrGU33PvQ84N3pbs4kz1CoCnm87HGUcq5ZT9gJbPy1TuKK2AoWRRdNePvQkRDRn0XpWt/FwC0DkPVy/KlbHV/N0oql7r8REDwVpGR3CQO1A/Q80DOh1+S6D6eb5wGPqAhhFabX7uW7rd9lQcEC5oXm8bnw5wirsNfljOv1S6/zfu/7Q+PN8c3jbh88GSR0PETZc2WkKlN0/lmn60Hf27yXQx2Hhsb1c+un/T2Cp4KUvFxC+L0wJIAUEw54rvtwunke8IAKsKl0Ey+3vczp5GlOJ0/zG35DqVVKfVk91aFqr0sa09vdb0P38Pjpx5/O+hpb2Vj9FtYZixnfm0H71nb6lve5VuP+tv0jxtMdcKvFovKpSmxs1OW/1MihCNdsvGbc1wW+FYCy0fvQ+IAD1EXqeOCnD3A4fJjfbv0tb/S+QUe6gz1de/hm+Td1lJTRE/EnWHJxydD4YsPFcbeP/CFC0f8UkbbSoKB7bTf9i/pdrbGhsYE7t9yJfYs7h3fpijTtW9uJNkZRvQqr3yIxJ0HHox3jvy6VBuAp6ynqZtaRLku7Ul82ngc8Zac4njjO3NRcFh9bTGlJKSWqhFe6XqHfdjcMOQtCYl5iwptbrRaFvyuke203PV/swS7212eKSbGgb3kffXf1EfnfCNHGKIl5iaz7xT5mQxKS1yRJR/WEGzQEPGEn+GHbD/n5V37O/FPz6evo452+dwCoDef3khT9i/tprmuGgO5KXBAYDno+fXviecBDKsQ9Rfdw4sIJ9s/fT19vH+WBcpZHlrOqaJXX5Uw/E8P9aXn2+2n5kLk+up65/zGX8LkwR3Ye8bqErJ6veV53CVntqtsFQGhHiCRJzdWM5pd9mEf/bITInQRcGE0CLowmARdGk4ALo0nAhdE8D3iwLcjs52cTPudcWDX7+dlEjkW8LiPvWa9YBP7aOSkd+FEA658s0PeFoW95HvBAV4Diw8VD4+KjxYRaQ16XkffUewr1tnPxkzqlsPZLwDPxPOD9c/rpru3GVs51Gsloks66Tq/LyHupR1JweV6wIzapr6Y0XTrnb1qOwVv+tAU7aJMuSNP8YLN8EpiM68BeZDsTRRjs+wy4sMsFWqLVP6efnnk9pIpTMntPQeqRlPNTZu8xadstZ79+FpVSMntPxXWQ3JWECt2F+Je2gKcL5RPRtIhn3+RqJvOnMFrObQThgIvlCDFRCtu2p95GUCn1qFLqgFLqALRMT21CeCTnGXz37r9ysZzJG2yy6sliJJPm7OuDB9/RXMfYFi689fIjP+9Hx7TM4ELkMwm4MJoEXBhNAi6MJgEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0bz/I4ev/RPHNO3gDKgERhc2bka+HOgD/hHLVWNsnbfWs71nhv1fOOKRhbEFmio6Ao+2Y/ablnT3T/RFMs+s4zZxbOHxuUF5Rqr8R9tAdfdP9EU665fx8prV+ouw7e0BVx3/8SsFuL8SwXw8T+XX378Sw5cGL6N8Mmbn9RYTQaa96O2gOvun5iVDw5jJ+L3538/Yuy7gGvej9oCvv2j7Sx7exltf9emq4TxZfpw5EMNjQ2s+Yc1BGp82h1K837UdpowdDxE+H1/te7OV+k2WWNmLHIeXBhNAi6M5vkx+GD/xIqf+HRBvecyPHcC2OFtGdnsWbUHgPYd7ZorGYNP9qPM4MJoEnBhNAm4MJoEXBhNAi6MJgEXRpOAC6N53wj2eJD41+KETjs98OJb4kTekEawuer+djfty5xz4N3f6KZjXQd2QjqtXcnzgKdjaVT/8LLOKqFIVaS8LiPvWXHLuTMGnAawIaTTWgbeB3xGmt7lvdhBGxubxPUJErUJr8vIe+FHwjB4AWEhFD5RiFL+X7Tea1qOwbse7HIaCBRA58PSJ3MyrHKL8JfDYIE1yyJ4p0zfmWgJeHpGmp57ehiYPyCz9xSEHwmjyhWFfymz91i0/dl3bpaZe6qscovYazHdZfianCYURpOAC6NJI1iRp6QRrBC5z+D79j3rYjmTt2rVfUB+NFk9e3b0kmt+UVV17eVH/j8rI41gxVVPAi6MJgEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0aTgAujScCF0Ty/ZW3TW5s4339+1PM7b9lJTXGN1+Vk5Psmq8Dilxdzuuv0qOf3PbiPz1d+XkNFV7jaG8HeUX4HVZGqoXEs6L97C/Ohyeq9191LdWn10Lii0KeNBTTRFvDV8dUsrVg68RfYwIdADcPrgbgsH5qsbqzdyJrqNbrL8C1tAd/bvJdDHYeGxvVz68d/wQkIbQthV9iktqSwV9quB933TVaB3Ud28+bZN4fGzyx5RmM1GVytjWD3t+0fMd72k23jbq+aFbayURcVgR8F4EVIPZHCXuTeeny+b7IKvHbytRFj3wX8am0E+53K77Bi24rJvXgASIA6rFwNeENjA1+46QsU/W2Ra+8xVQ2NDTz0g4corCvUXUpmmhvB6lvvqwIS+3JY1eoYBLcFIQB2nXOYwnXulTco/Yn/m6za/bKq7FjyZ0G7KkhvSJNemfYk2MIM+RPwQkhv9v9sKvzF84Dvqtvl9VvmbEST1RzOZHrpjw/9EYCjO45qrmQM0ghWCPdJwIXRJODCaBJwYTQJuDCaBFwYTQKegd1vkzrrtDa0223S5/x3/j3VkSJxyvkmOHEuQbIlqbkif5KAZ9D3Uh+dDzg9hFLvpehY20HyiL8CdGbzGZrubgLgk7/4hKY7m7AH5Cv7K0nAMwitDI34CkyVKwI1Hl2EPkHRL0VRwcvLY6eh6K4iVIH/1/T2mgQ8g+CCIMGFQWfvFELksQgq5K/wxDbGUGGnJlWgmLl9puaK/EkCPobI4xGwQEUUBfcX6C5nFCtsUflkJVhQdHcR4QVh3SX5Uv5cbOWxYG2Qgi8XELwt6LvZe1BsY4yeP/RQ+XSl7lJ8SwI+jqKn/HujAziz+KwXZ+kuw9fkEEUYTQIujCaNYEWekkawQkxmBn/LxXKmwvk98qHJag673HNqaE7055mjT5NGsOKqJwEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0aTgAujScCF0STgwmje3rLmk+ag2fi+ySpQ/Vw1H1/6eNTzB79xkFuvuVVDRRnMAu4C5gCFQA/QjHNLwWFvSpB7MseRD01W77/hfmrKhztEzyzyyfIRNwLrcY4RWoAPgDBO6G9GAu4HuTZZTZxL0PlqJ7ENMQJRbxYK2rJwC+tq1014+0tvXqL3WC/xDXGsoEtHqCHgfpxwvwv8JzC4+p0CPFwEQE/ANTcHnahcm6x2/bqLlmdauPD9C8yon0H518tdD/qLB1/k9ROvD42fW52pd8iwk8+epPVXrTQ93cRnv/dZd4I+BxhckOB3DIcbnPtSPLwxTE/ANTcHnagrm6w+vP7h7C8KgN1t0/ovrbT+ayuz/n0WxXcVu1QhvPrBqyPG69ZMbDYfODvAB1s/oOnbTdz+1u0UfGYaFzf69K/bfvnnvTjH44N2TN/bjUdPwDU3B52oF256gZsbbh7uQ5nlD3Pg6IDzbzkFBCAYDxKY4e4M/tKcl7jxn28cfuKm8bfvea/HeaBw1jSsdWFNw+5PPS4FWoGTwCHgT6b3rbKRY/BxBGcFqd5bPeHt2/6tjea/aSY0N0T87+MUrypGKXfvbSxbUsbiry6e8PbvfuldLr56kbKVZdR8v4bobdHpL+oUzhmTIuBu4L9wPmR2IAHPZ7GvxAjPD1O4pND1YE/WDTtvYGDHANGFLgR7UALYAzyI83nrWuA0EHPvLcciAZ9GVpFF0VJ/L/cWrgoTrvJgoc7/w5mxl+J86FyIc+jyEfC++28/SJaN8JAsGzG9ZNkIcdWTgAujScCF0STgwmgScGE0CbgwmgRcGE0CLowmARdGk4ALo0nAhdEk4MJoEnBhNAm4MJoEXBgtx+vBVSdw1L1ypqwSuKC7iCykxulxvW3bWReByfWOnqO2bd8+yYJcp5Q64Of6QGr0mhyiCKNJwIXRcg34j12pYvr4vT6QGj2V04dMIfKNHKIIo0nAhdEk4MJoEnBhNAm4MNr/A0vg0SO2dsmQAAAAAElFTkSuQmCC\n",
+      "text/plain": [
+       "<Figure size 216x216 with 1 Axes>"
+      ]
+     },
+     "metadata": {},
+     "output_type": "display_data"
+    },
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "after iteration 8\n",
+      "iter    0   |   diff: 0.00000   |   V(start): 0.590 \n",
+      "Terminated\n"
+     ]
+    },
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAALgAAAC4CAYAAABQMybHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvDW2N/gAADcpJREFUeJzt3X1sXNWZx/HvuTPjGb+Mx46dKTgJOHVCXCgLwSSgBPJSIEpSRLMorRLYKEvT0rgKossu0M2+NMKrsm23K1R2FVGVsqtUxFLZbldCaZqlW9ouQqkCQWEhCRAn5JXYie343Z6Xu3/c2Mbx2OOxfe+5c/J8/vGc0R3N46ufj+/cufc8yrZthDCVpbsAIdwkARdGk4ALo0nAhdEk4MJoEnBhNAm4MJoEXBhNAi6MFsy2gVLqUeBRZ1RcB7UulyREdiUlR+ns7FTZtlO5fFWv1O32zp1fm1Jhbqmv3wrA7t2NmisZ28aNGwDYt++/NVcytlWr7gP8vR8Btm/fTlNTU9aAyyGKMJoEXBhNAi6MJgEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0aTgAujScCF0bJeD+6GlmQLv+j6BR8NfESf3UeJVUJVsIoN0Q3MDM7UUdIIjx17jAvJC6Oef/b6Z6mOVHtfUAab3trE+f7zo57fectOaoprNFQ0kl/2oZaAv3DpBc4kz7CgYAHxQJz2VDsfJj7kUvoSM9Ef8EG3Fd9GvCA+NC4NlGqsJrM7yu+gKlI1NI4FYxqrGU33PvQ84N3pbs4kz1CoCnm87HGUcq5ZT9gJbPy1TuKK2AoWRRdNePvQkRDRn0XpWt/FwC0DkPVy/KlbHV/N0oql7r8REDwVpGR3CQO1A/Q80DOh1+S6D6eb5wGPqAhhFabX7uW7rd9lQcEC5oXm8bnw5wirsNfljOv1S6/zfu/7Q+PN8c3jbh88GSR0PETZc2WkKlN0/lmn60Hf27yXQx2Hhsb1c+un/T2Cp4KUvFxC+L0wJIAUEw54rvtwunke8IAKsKl0Ey+3vczp5GlOJ0/zG35DqVVKfVk91aFqr0sa09vdb0P38Pjpx5/O+hpb2Vj9FtYZixnfm0H71nb6lve5VuP+tv0jxtMdcKvFovKpSmxs1OW/1MihCNdsvGbc1wW+FYCy0fvQ+IAD1EXqeOCnD3A4fJjfbv0tb/S+QUe6gz1de/hm+Td1lJTRE/EnWHJxydD4YsPFcbeP/CFC0f8UkbbSoKB7bTf9i/pdrbGhsYE7t9yJfYs7h3fpijTtW9uJNkZRvQqr3yIxJ0HHox3jvy6VBuAp6ynqZtaRLku7Ul82ngc8Zac4njjO3NRcFh9bTGlJKSWqhFe6XqHfdjcMOQtCYl5iwptbrRaFvyuke203PV/swS7212eKSbGgb3kffXf1EfnfCNHGKIl5iaz7xT5mQxKS1yRJR/WEGzQEPGEn+GHbD/n5V37O/FPz6evo452+dwCoDef3khT9i/tprmuGgO5KXBAYDno+fXviecBDKsQ9Rfdw4sIJ9s/fT19vH+WBcpZHlrOqaJXX5Uw/E8P9aXn2+2n5kLk+up65/zGX8LkwR3Ye8bqErJ6veV53CVntqtsFQGhHiCRJzdWM5pd9mEf/bITInQRcGE0CLowmARdGk4ALo0nAhdE8D3iwLcjs52cTPudcWDX7+dlEjkW8LiPvWa9YBP7aOSkd+FEA658s0PeFoW95HvBAV4Diw8VD4+KjxYRaQ16XkffUewr1tnPxkzqlsPZLwDPxPOD9c/rpru3GVs51Gsloks66Tq/LyHupR1JweV6wIzapr6Y0XTrnb1qOwVv+tAU7aJMuSNP8YLN8EpiM68BeZDsTRRjs+wy4sMsFWqLVP6efnnk9pIpTMntPQeqRlPNTZu8xadstZ79+FpVSMntPxXWQ3JWECt2F+Je2gKcL5RPRtIhn3+RqJvOnMFrObQThgIvlCDFRCtu2p95GUCn1qFLqgFLqALRMT21CeCTnGXz37r9ysZzJG2yy6sliJJPm7OuDB9/RXMfYFi689fIjP+9Hx7TM4ELkMwm4MJoEXBhNAi6MJgEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0bz/I4ev/RPHNO3gDKgERhc2bka+HOgD/hHLVWNsnbfWs71nhv1fOOKRhbEFmio6Ao+2Y/ablnT3T/RFMs+s4zZxbOHxuUF5Rqr8R9tAdfdP9EU665fx8prV+ouw7e0BVx3/8SsFuL8SwXw8T+XX378Sw5cGL6N8Mmbn9RYTQaa96O2gOvun5iVDw5jJ+L3538/Yuy7gGvej9oCvv2j7Sx7exltf9emq4TxZfpw5EMNjQ2s+Yc1BGp82h1K837UdpowdDxE+H1/te7OV+k2WWNmLHIeXBhNAi6M5vkx+GD/xIqf+HRBvecyPHcC2OFtGdnsWbUHgPYd7ZorGYNP9qPM4MJoEnBhNAm4MJoEXBhNAi6MJgEXRpOAC6N53wj2eJD41+KETjs98OJb4kTekEawuer+djfty5xz4N3f6KZjXQd2QjqtXcnzgKdjaVT/8LLOKqFIVaS8LiPvWXHLuTMGnAawIaTTWgbeB3xGmt7lvdhBGxubxPUJErUJr8vIe+FHwjB4AWEhFD5RiFL+X7Tea1qOwbse7HIaCBRA58PSJ3MyrHKL8JfDYIE1yyJ4p0zfmWgJeHpGmp57ehiYPyCz9xSEHwmjyhWFfymz91i0/dl3bpaZe6qscovYazHdZfianCYURpOAC6NJI1iRp6QRrBC5z+D79j3rYjmTt2rVfUB+NFk9e3b0kmt+UVV17eVH/j8rI41gxVVPAi6MJgEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0aTgAujScCF0Ty/ZW3TW5s4339+1PM7b9lJTXGN1+Vk5Psmq8Dilxdzuuv0qOf3PbiPz1d+XkNFV7jaG8HeUX4HVZGqoXEs6L97C/Ohyeq9191LdWn10Lii0KeNBTTRFvDV8dUsrVg68RfYwIdADcPrgbgsH5qsbqzdyJrqNbrL8C1tAd/bvJdDHYeGxvVz68d/wQkIbQthV9iktqSwV9quB933TVaB3Ud28+bZN4fGzyx5RmM1GVytjWD3t+0fMd72k23jbq+aFbayURcVgR8F4EVIPZHCXuTeeny+b7IKvHbytRFj3wX8am0E+53K77Bi24rJvXgASIA6rFwNeENjA1+46QsU/W2Ra+8xVQ2NDTz0g4corCvUXUpmmhvB6lvvqwIS+3JY1eoYBLcFIQB2nXOYwnXulTco/Yn/m6za/bKq7FjyZ0G7KkhvSJNemfYk2MIM+RPwQkhv9v9sKvzF84Dvqtvl9VvmbEST1RzOZHrpjw/9EYCjO45qrmQM0ghWCPdJwIXRJODCaBJwYTQJuDCaBFwYTQKegd1vkzrrtDa0223S5/x3/j3VkSJxyvkmOHEuQbIlqbkif5KAZ9D3Uh+dDzg9hFLvpehY20HyiL8CdGbzGZrubgLgk7/4hKY7m7AH5Cv7K0nAMwitDI34CkyVKwI1Hl2EPkHRL0VRwcvLY6eh6K4iVIH/1/T2mgQ8g+CCIMGFQWfvFELksQgq5K/wxDbGUGGnJlWgmLl9puaK/EkCPobI4xGwQEUUBfcX6C5nFCtsUflkJVhQdHcR4QVh3SX5Uv5cbOWxYG2Qgi8XELwt6LvZe1BsY4yeP/RQ+XSl7lJ8SwI+jqKn/HujAziz+KwXZ+kuw9fkEEUYTQIujCaNYEWekkawQkxmBn/LxXKmwvk98qHJag673HNqaE7055mjT5NGsOKqJwEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0aTgAujScCF0STgwmje3rLmk+ag2fi+ySpQ/Vw1H1/6eNTzB79xkFuvuVVDRRnMAu4C5gCFQA/QjHNLwWFvSpB7MseRD01W77/hfmrKhztEzyzyyfIRNwLrcY4RWoAPgDBO6G9GAu4HuTZZTZxL0PlqJ7ENMQJRbxYK2rJwC+tq1014+0tvXqL3WC/xDXGsoEtHqCHgfpxwvwv8JzC4+p0CPFwEQE/ANTcHnahcm6x2/bqLlmdauPD9C8yon0H518tdD/qLB1/k9ROvD42fW52pd8iwk8+epPVXrTQ93cRnv/dZd4I+BxhckOB3DIcbnPtSPLwxTE/ANTcHnagrm6w+vP7h7C8KgN1t0/ovrbT+ayuz/n0WxXcVu1QhvPrBqyPG69ZMbDYfODvAB1s/oOnbTdz+1u0UfGYaFzf69K/bfvnnvTjH44N2TN/bjUdPwDU3B52oF256gZsbbh7uQ5nlD3Pg6IDzbzkFBCAYDxKY4e4M/tKcl7jxn28cfuKm8bfvea/HeaBw1jSsdWFNw+5PPS4FWoGTwCHgT6b3rbKRY/BxBGcFqd5bPeHt2/6tjea/aSY0N0T87+MUrypGKXfvbSxbUsbiry6e8PbvfuldLr56kbKVZdR8v4bobdHpL+oUzhmTIuBu4L9wPmR2IAHPZ7GvxAjPD1O4pND1YE/WDTtvYGDHANGFLgR7UALYAzyI83nrWuA0EHPvLcciAZ9GVpFF0VJ/L/cWrgoTrvJgoc7/w5mxl+J86FyIc+jyEfC++28/SJaN8JAsGzG9ZNkIcdWTgAujScCF0STgwmgScGE0CbgwmgRcGE0CLowmARdGk4ALo0nAhdEk4MJoEnBhNAm4MJoEXBgtx+vBVSdw1L1ypqwSuKC7iCykxulxvW3bWReByfWOnqO2bd8+yYJcp5Q64Of6QGr0mhyiCKNJwIXRcg34j12pYvr4vT6QGj2V04dMIfKNHKIIo0nAhdEk4MJoEnBhNAm4MNr/A0vg0SO2dsmQAAAAAElFTkSuQmCC\n",
+      "text/plain": [
+       "<Figure size 216x216 with 1 Axes>"
+      ]
+     },
+     "metadata": {},
+     "output_type": "display_data"
+    },
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "after iteration 9\n",
+      "iter    0   |   diff: 0.00000   |   V(start): 0.590 \n",
+      "Terminated\n"
+     ]
+    },
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAALgAAAC4CAYAAABQMybHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvDW2N/gAADcpJREFUeJzt3X1sXNWZx/HvuTPjGb+Mx46dKTgJOHVCXCgLwSSgBPJSIEpSRLMorRLYKEvT0rgKossu0M2+NMKrsm23K1R2FVGVsqtUxFLZbldCaZqlW9ouQqkCQWEhCRAn5JXYie343Z6Xu3/c2Mbx2OOxfe+5c/J8/vGc0R3N46ufj+/cufc8yrZthDCVpbsAIdwkARdGk4ALo0nAhdEk4MJoEnBhNAm4MJoEXBhNAi6MFsy2gVLqUeBRZ1RcB7UulyREdiUlR+ns7FTZtlO5fFWv1O32zp1fm1Jhbqmv3wrA7t2NmisZ28aNGwDYt++/NVcytlWr7gP8vR8Btm/fTlNTU9aAyyGKMJoEXBhNAi6MJgEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0aTgAujScCF0bJeD+6GlmQLv+j6BR8NfESf3UeJVUJVsIoN0Q3MDM7UUdIIjx17jAvJC6Oef/b6Z6mOVHtfUAab3trE+f7zo57fectOaoprNFQ0kl/2oZaAv3DpBc4kz7CgYAHxQJz2VDsfJj7kUvoSM9Ef8EG3Fd9GvCA+NC4NlGqsJrM7yu+gKlI1NI4FYxqrGU33PvQ84N3pbs4kz1CoCnm87HGUcq5ZT9gJbPy1TuKK2AoWRRdNePvQkRDRn0XpWt/FwC0DkPVy/KlbHV/N0oql7r8REDwVpGR3CQO1A/Q80DOh1+S6D6eb5wGPqAhhFabX7uW7rd9lQcEC5oXm8bnw5wirsNfljOv1S6/zfu/7Q+PN8c3jbh88GSR0PETZc2WkKlN0/lmn60Hf27yXQx2Hhsb1c+un/T2Cp4KUvFxC+L0wJIAUEw54rvtwunke8IAKsKl0Ey+3vczp5GlOJ0/zG35DqVVKfVk91aFqr0sa09vdb0P38Pjpx5/O+hpb2Vj9FtYZixnfm0H71nb6lve5VuP+tv0jxtMdcKvFovKpSmxs1OW/1MihCNdsvGbc1wW+FYCy0fvQ+IAD1EXqeOCnD3A4fJjfbv0tb/S+QUe6gz1de/hm+Td1lJTRE/EnWHJxydD4YsPFcbeP/CFC0f8UkbbSoKB7bTf9i/pdrbGhsYE7t9yJfYs7h3fpijTtW9uJNkZRvQqr3yIxJ0HHox3jvy6VBuAp6ynqZtaRLku7Ul82ngc8Zac4njjO3NRcFh9bTGlJKSWqhFe6XqHfdjcMOQtCYl5iwptbrRaFvyuke203PV/swS7212eKSbGgb3kffXf1EfnfCNHGKIl5iaz7xT5mQxKS1yRJR/WEGzQEPGEn+GHbD/n5V37O/FPz6evo452+dwCoDef3khT9i/tprmuGgO5KXBAYDno+fXviecBDKsQ9Rfdw4sIJ9s/fT19vH+WBcpZHlrOqaJXX5Uw/E8P9aXn2+2n5kLk+up65/zGX8LkwR3Ye8bqErJ6veV53CVntqtsFQGhHiCRJzdWM5pd9mEf/bITInQRcGE0CLowmARdGk4ALo0nAhdE8D3iwLcjs52cTPudcWDX7+dlEjkW8LiPvWa9YBP7aOSkd+FEA658s0PeFoW95HvBAV4Diw8VD4+KjxYRaQ16XkffUewr1tnPxkzqlsPZLwDPxPOD9c/rpru3GVs51Gsloks66Tq/LyHupR1JweV6wIzapr6Y0XTrnb1qOwVv+tAU7aJMuSNP8YLN8EpiM68BeZDsTRRjs+wy4sMsFWqLVP6efnnk9pIpTMntPQeqRlPNTZu8xadstZ79+FpVSMntPxXWQ3JWECt2F+Je2gKcL5RPRtIhn3+RqJvOnMFrObQThgIvlCDFRCtu2p95GUCn1qFLqgFLqALRMT21CeCTnGXz37r9ysZzJG2yy6sliJJPm7OuDB9/RXMfYFi689fIjP+9Hx7TM4ELkMwm4MJoEXBhNAi6MJgEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0bz/I4ev/RPHNO3gDKgERhc2bka+HOgD/hHLVWNsnbfWs71nhv1fOOKRhbEFmio6Ao+2Y/ablnT3T/RFMs+s4zZxbOHxuUF5Rqr8R9tAdfdP9EU665fx8prV+ouw7e0BVx3/8SsFuL8SwXw8T+XX378Sw5cGL6N8Mmbn9RYTQaa96O2gOvun5iVDw5jJ+L3538/Yuy7gGvej9oCvv2j7Sx7exltf9emq4TxZfpw5EMNjQ2s+Yc1BGp82h1K837UdpowdDxE+H1/te7OV+k2WWNmLHIeXBhNAi6M5vkx+GD/xIqf+HRBvecyPHcC2OFtGdnsWbUHgPYd7ZorGYNP9qPM4MJoEnBhNAm4MJoEXBhNAi6MJgEXRpOAC6N53wj2eJD41+KETjs98OJb4kTekEawuer+djfty5xz4N3f6KZjXQd2QjqtXcnzgKdjaVT/8LLOKqFIVaS8LiPvWXHLuTMGnAawIaTTWgbeB3xGmt7lvdhBGxubxPUJErUJr8vIe+FHwjB4AWEhFD5RiFL+X7Tea1qOwbse7HIaCBRA58PSJ3MyrHKL8JfDYIE1yyJ4p0zfmWgJeHpGmp57ehiYPyCz9xSEHwmjyhWFfymz91i0/dl3bpaZe6qscovYazHdZfianCYURpOAC6NJI1iRp6QRrBC5z+D79j3rYjmTt2rVfUB+NFk9e3b0kmt+UVV17eVH/j8rI41gxVVPAi6MJgEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0aTgAujScCF0Ty/ZW3TW5s4339+1PM7b9lJTXGN1+Vk5Psmq8Dilxdzuuv0qOf3PbiPz1d+XkNFV7jaG8HeUX4HVZGqoXEs6L97C/Ohyeq9191LdWn10Lii0KeNBTTRFvDV8dUsrVg68RfYwIdADcPrgbgsH5qsbqzdyJrqNbrL8C1tAd/bvJdDHYeGxvVz68d/wQkIbQthV9iktqSwV9quB933TVaB3Ud28+bZN4fGzyx5RmM1GVytjWD3t+0fMd72k23jbq+aFbayURcVgR8F4EVIPZHCXuTeeny+b7IKvHbytRFj3wX8am0E+53K77Bi24rJvXgASIA6rFwNeENjA1+46QsU/W2Ra+8xVQ2NDTz0g4corCvUXUpmmhvB6lvvqwIS+3JY1eoYBLcFIQB2nXOYwnXulTco/Yn/m6za/bKq7FjyZ0G7KkhvSJNemfYk2MIM+RPwQkhv9v9sKvzF84Dvqtvl9VvmbEST1RzOZHrpjw/9EYCjO45qrmQM0ghWCPdJwIXRJODCaBJwYTQJuDCaBFwYTQKegd1vkzrrtDa0223S5/x3/j3VkSJxyvkmOHEuQbIlqbkif5KAZ9D3Uh+dDzg9hFLvpehY20HyiL8CdGbzGZrubgLgk7/4hKY7m7AH5Cv7K0nAMwitDI34CkyVKwI1Hl2EPkHRL0VRwcvLY6eh6K4iVIH/1/T2mgQ8g+CCIMGFQWfvFELksQgq5K/wxDbGUGGnJlWgmLl9puaK/EkCPobI4xGwQEUUBfcX6C5nFCtsUflkJVhQdHcR4QVh3SX5Uv5cbOWxYG2Qgi8XELwt6LvZe1BsY4yeP/RQ+XSl7lJ8SwI+jqKn/HujAziz+KwXZ+kuw9fkEEUYTQIujCaNYEWekkawQkxmBn/LxXKmwvk98qHJag673HNqaE7055mjT5NGsOKqJwEXRpOAC6NJwIXRJODCaBJwYTQJuDCaBFwYTQIujCYBF0aTgAujScCF0STgwmje3rLmk+ag2fi+ySpQ/Vw1H1/6eNTzB79xkFuvuVVDRRnMAu4C5gCFQA/QjHNLwWFvSpB7MseRD01W77/hfmrKhztEzyzyyfIRNwLrcY4RWoAPgDBO6G9GAu4HuTZZTZxL0PlqJ7ENMQJRbxYK2rJwC+tq1014+0tvXqL3WC/xDXGsoEtHqCHgfpxwvwv8JzC4+p0CPFwEQE/ANTcHnahcm6x2/bqLlmdauPD9C8yon0H518tdD/qLB1/k9ROvD42fW52pd8iwk8+epPVXrTQ93cRnv/dZd4I+BxhckOB3DIcbnPtSPLwxTE/ANTcHnagrm6w+vP7h7C8KgN1t0/ovrbT+ayuz/n0WxXcVu1QhvPrBqyPG69ZMbDYfODvAB1s/oOnbTdz+1u0UfGYaFzf69K/bfvnnvTjH44N2TN/bjUdPwDU3B52oF256gZsbbh7uQ5nlD3Pg6IDzbzkFBCAYDxKY4e4M/tKcl7jxn28cfuKm8bfvea/HeaBw1jSsdWFNw+5PPS4FWoGTwCHgT6b3rbKRY/BxBGcFqd5bPeHt2/6tjea/aSY0N0T87+MUrypGKXfvbSxbUsbiry6e8PbvfuldLr56kbKVZdR8v4bobdHpL+oUzhmTIuBu4L9wPmR2IAHPZ7GvxAjPD1O4pND1YE/WDTtvYGDHANGFLgR7UALYAzyI83nrWuA0EHPvLcciAZ9GVpFF0VJ/L/cWrgoTrvJgoc7/w5mxl+J86FyIc+jyEfC++28/SJaN8JAsGzG9ZNkIcdWTgAujScCF0STgwmgScGE0CbgwmgRcGE0CLowmARdGk4ALo0nAhdEk4MJoEnBhNAm4MJoEXBgtx+vBVSdw1L1ypqwSuKC7iCykxulxvW3bWReByfWOnqO2bd8+yYJcp5Q64Of6QGr0mhyiCKNJwIXRcg34j12pYvr4vT6QGj2V04dMIfKNHKIIo0nAhdEk4MJoEnBhNAm4MNr/A0vg0SO2dsmQAAAAAElFTkSuQmCC\n",
+      "text/plain": [
+       "<Figure size 216x216 with 1 Axes>"
+      ]
+     },
+     "metadata": {},
+     "output_type": "display_data"
+    }
+   ],
+   "source": [
+    "state_values = {s : 0 for s in mdp.get_all_states()}\n",
+    "\n",
+    "for i in range(10):\n",
+    "    print(\"after iteration %i\"%i)\n",
+    "    state_values = value_iteration(mdp, state_values, num_iter=1)\n",
+    "    draw_policy(mdp, state_values)\n",
+    "# please ignore iter 0 at each step"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 21,
+   "metadata": {},
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "after iteration 29\n",
+      "iter    0   |   diff: 0.00000   |   V(start): 0.198 \n",
+      "Terminated\n"
+     ]
+    },
+    {
+     "data": {
+      "image/png": "iVBORw0KGgoAAAANSUhEUgAAALgAAAC4CAYAAABQMybHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvDW2N/gAAIABJREFUeJztnXl8VNXd/9+zZWay7xsEkhCWsBN2iAQExAVw37U/d0sXtfrz6aPPU2uhL221au3jY7WupbVirT/rghYtKIgIhD0BkpCwJJB93yaZzPL745oZhpkkc2fO6DC579fLl/fce+eTO9zvPXPuOedzviq73Y6CQqii/r4vQEEhkCgBrhDSKAGuENIoAa4Q0igBrhDSKAGuENIoAa4Q0igBrhDSKAGuENJohzpBpVLdA9wjlSJmwoQAX5KCwtAYDIcxmUyqoc5TyRmqV6lm2fPyxAzt79u3F4B58+YL0du58xsACgoWC9ED2Lr1SwBWrLhYiN6mTf8C4IorrhSiB/DPf74PwI033iRE7+23/wbAXXfdLUTv1VdfAeD++x8QotfP22+/TV1d3ZABrjRRFEIaJcAVQholwBVCmiFfMr2lN7yX05NO0xXfhVVrRWvWYuwwknEoA323XrbevoJ9mI1mt/1Tvp5CREeET9e4c95Oeo29bvtnFs4ksjNStt7WGVvpMfS47Z9/cD7R3dGy9TZN3IQpzOS2f3HpYmJNsbL1AD7M/pAuXZfb/otPXkxcb5xsvQ2pG+jUdrrtv7LuShL6Eny6xtejX6dD0+G2/6b2m0iyJvmk2Y+wAD8++zimGBNRDVHou/SYDWY6EzrpM/T5FOD9xNbHYug2OMo6s87va41vjMdoMgrTTGpOwtjr1AuzhPmll9KWQoTZ+RDrLb7/+/WT3plOpNn5EOut/mlmmDKItjgfYoPVMMjZ3pFlziLGFuMoG23GQc72DiEBbtFZMMWY0Jg15HyTgwrp5damtsGQ77mDk3w6mfj6eAFX6SStJo3ExkRheiPqR5DSkiJMb3TzaNLb0oXpAYxpG8PIzpHC9MZ3jSezJ1OYHsAk8yTG9I0RqikkwDUWDWqLGmuYlZKCEqIao4hsiiSqIQqNVeM4T2VXYVfJ62asH1lPe3y7o5xZkumXHkBNWg2tsa2Ock55jrTRLyXzoTyTfIbmmGZHOfdkrvOgXb7eqfhTNEY2OspTz0z1Sw+gIqaCOmOdozyzYaZfmqURpdToaxzl+W3+d/ceDjvMae1pR7nAVOC3ppAAV9lVjD4wmspplZhiTJhiTNSPqSfMFMas7bOIbY5lWss0FjYs5LO0z9iZuNNr7dbkVpfy3H1zATBYDNxecjtH447yWcZnsq63ObHZpbzgwAIAVlSsILY3ls+yP6M0odRrvYb4BpfyoqJFAKS1pbGsZBl7Ru1hV9Yur/XqYupcykuOLHFsX7njSpqimtg+eTsNsQ3nfnRAqiOrXcrLji0DILc8l+zKbAqnFVKWVea1XpWxyqUsIsBPhJ1wKQdNgAPEVccRUxtDqi6VRGMiG/M20hLZAqPg4a8fdpx35ekrqTHWsNtL3UmFk3hh4wsDHp/aNBWNXcOnMq71rk/u4ubdN3s8ZsfO9Yev54n8J7zWW7J3CY999NiAxxecWECnvpMPvdSbc3wOv13/2wGPG3uNXLT3It5a+pbX13jLrlu489M7BzxesLvA7UEdjJuKbuLazdey8ZqNXn9mKNZtWEfnwk56It1f3H1FSIDbVXa64rqIbI6kvree+t56Ik5G0DK5hUMJh3go7yEmtE1gWe0yPkn/hONRx73W7tP08ci8R9z2h1nDuOPoHRTHF7MzdSfs/qnXmt9kfMMx4zG3/Rcev5AEUwKbszZj0Vi81muJaOE3K37jtj+5PZmLD1/MzuydlCWXQYmXgip4/ornPR66fMflNMQ0sHfsXq+vD+DUyFP86cY/ue3POZHD+OPj2T19N81xzR4+6ZmY1hhiW33r2RmMsJ6w4Atwm9pGWX4Zhg4DxjYjaqua1lSpaRHdIL1pl8SUUBLj7R0eGrPGzEuTXxKmB7Ale4tQvfroetbPXy9U84MFHwjVK88qpzyrXKhmMCEkwNU2NckVyXQkdtCe3I5NYyOsJ4ykk0mklIvrXVBQkIuwl8yRh8V1QQHkbc0Tqgcwb+c8oXoF+/1/CTqbFUdWCNUDWH18tVC9G2pvAGDGmRnCNO9ovwOA/JJ8tswU+yuqDNUrhDRKgCvIxthlZGzJWACm7J0iRHP++1I348L/t9A5HiEAJcAVZNNr6KXH0INVbaUpqUmIZmtyK3aVndakVr9Hv89GCXAF2dg0NvbO20tdWh3VGdVDf8ALymeW05bYxuH8w0L0+pH9kqlWi30mgl0PQKsVNh4GgMHg/8SkcwkPDxeqFxk5+OzKxumNNE5vJBLvZmFGRw8xuzIa9v1w37ebQ8/E1Gg0Q54DPljWYI/X5ysoBIq0tHSqq6v9t6ypVKp7VCrVHpVKtQe8H8pVUAgGZNfgs2aJeQPYs6cQgAULFgrR27HjawCWLLlQiB7AF19IfbKXXbZSiN7GjR8DcMMNNwrRA9iw4W0A7rzzLiF6r732KgAPPPAzIXq///1zAPziFwPP1fGFV199VUwNrqBwPqMEuEJIowS4QkgjrP/r0IWHMIe7m4QnbptIeLv8Lqy9F+z1aBCe9s00n03H38z9xqNJeNaeWUR1RcnW2zJ1Cya9u0k4vzifGFOMh08MzodjPqRb1+22f8WJFT4ZhAHeSXvHo0n4itorfDIJvxb9Gh1qDwbhjptItib7dI1/UP+BNlWb2/67rXeTSqpPmv2I7eAFYupi0Hc5Da1as39/Iq4hzsV07K8eQEJTgovpOKzPP5Nwcmsy4T3Oh9hfk7BogzB4MAnb/OuLz+pzNQiH2/zvhx9rH0uc3fkgh+O/pvAAT6xMJK7Ot9rGE8mnk0lo8G05goFIq0kjqcm/5QjOJqMhg9RW/2qas8luzRZqEAYY1zWOTFOmML1J5knk9OUI0wOYbpvOBMFrXwoP8MZRjXQkOH/CRh0ZBUB6dzrTmqexLWWbx3U6BuJc03FWaRYAGpuGZZXLOBp/lMroSlnXeK7peGyFNHFoUu0kwi3h7Evbh1Vj9VqvKqmKpijnnIxJVZMAiDJFMfPETPZn7qct3P0neCCOxx6nPrzeUc6rd04dzivOoymuiVPpp2TN2SiLKKNWX+soz2uVpg4n1SSRVp3G0clH6dP3ea13rkF4sWmx9xczAAfUBzhlP+Uor7D7P31YeIC3pbjeyHfWv+NSXlS3iBcmvOD1eGhLUotL+W9v/M2lvLB6IbtTd7NDxjU2JbhOEPrLq39xbNuxU3CygOcWPOe1Xn1svUv5jZfecCnnnchj44yNeOtePNcg/PIfXnYpW1VWapJq2Hih937Ic03CLzzj6nOdWDSRj6/62Gu9EzpXg7CIAD+mOuby0K6wBmGAT9o5iZv23oTaLnXQ9DvoJ7dOJtISyeHYw7SGtQ4m4cL4/eNZdXAVSSapSbE7RbIrGywGpjZNpU3fxtH4o1A7mIoriwoXsXq/0wiwN13yN86snolVZWV/6n5sKpvXenNK53DNrmscC/4cHHUQgNTWVFLaUzgTf4b66PrBJFzIP51PweEC0uultVGOjDniODaxYiJmnVmWAx7gsqrLWP31alR2KYKOjZc8qVnlWWitWk5lnaLX4P5SPxA/3fFTrvrsKj54QJyFbt2GdegW6ehK8f4XfiiEB3iPpof3R7/vtv99+/tEm6Np1Xsf3P3sSPdcP2/q2USbvk322ijNxmY2jnev/f495t+o7WpMOveekcGwqq1szd3qfsAOMaYYWc2TfipGV1AxusJt/95Je+nR92DTeP8AAvQYe9i90H0tg8L5heh79Jgi5H3n8wXhAT4QNpXNp+AejFaDWL1erfc1mFeo8Cm4B6M73L0b0R9sGlvIBjcoAz0KIY6wGnzqlqlDnySDmV/NHPokmczfJSabRD8XHhI3sQtgdYVYgzDA9TXXC9W7s11aPGha9TRhmvfZ7gMk0/GuRd6vAOYNSg2uIBu1RU3GkQwAEqrEjFGk7U8DYOQesf3/SoAryCasJwyNTXLUJJwRE+ApxdL6OYmliYrpWOH7pSeyh1MTT2HRWjg+w/tl+AajYqnUY1RxYYVQ0/F31ouiEFoUFxRTOrcUi977NRwHoyO9g50/3IkpQWyPjuLJVDgvGTkyg6qqKsWTqTC8kV2DT5/u/SSkwThwYD8As2bNFqIn2uMJTp+nuEah9G/9gx/8H0F6sH79nwFYs+ZHQvT++McXAXjssV8K0Vu79lcAPPPMs0L0+nnuuefE1OAKCuczSoArhDRKgCuENMK6CQ9fdJi+cPcJ8+O+GEd4m3zrkWiPJwj2eT4AxAIbcKYmyQRuA3oA94wmQ/JexnsezSArT68k3uxbKsW/Jv7VY5LVa5uuJdEiP5Xi86rnPfon77Hd47N/8tedv6bF3uK2/8HwBxmhGeGTZj/C+8Gja6MJ63J6HLW9/v0J0R5PCIzPUyQju0YSZXGaoEUkWR3dO1qoJ3OsfSzxOB86Ef7JiZqJJKidI6ORKvnZp89F+J2NPxVPbI245ESiPZ4QGJ+nSHI6chjVPUqoZq4pl6zeLGF6M+wzhPsn5+jmMEUnZr3xfoQHePPoZjoTncsUjCySJs+o7WrizHE06eWtJz2Qx9MfBvJ5+sQMpKYJ4MWiqF5RHlXukrR1dpOzKzWiM4IeY48szyjAUeNRzujOOMr5nfmANHHKYDLQHSVvnvl+1X5OIdY/ubtvNxVWp8njCsMVfmsKD/D21HaX8s8//jkAk9smY7AZKIou4t2Md73WO9fjKSLAz/V5+hXg4/28GA+cjjjtUn7wgwcd2znHc+gN66Uwr5Bj49xTIQ7EKf0pOGv1iX7NzLJM6XjOKfYt2ue13jGV698WEeBHrEfgrOc2KAP8gi8uYO3WtQMen9Axgag+7xfZuWjLRTyy7REenvXw0Cd7yboN6yhTl1ER624Jk42nl0w/WVyzmDXvrSG50fNCOlqLlqxTWbIC/JYjt3Dn3wdOBDvi5AiK5xZ7rffj4h9zzT+u4YvHvvD6M0OxbsM64q6IozdJnLNKeIBXhVfxs+nuK5OmmdKY2jqVr5K+olvr/c+hiBes71JXCCrYeKlnx/zkosm0xLdwJv2Mx+MD0ZjeyN/X/N1tf0JNAsnVyRybcgxLmPcTp3TdOll/31tUFoFTCfkOZxPWGGuoMdZ8V38uZCme4n0t6w1NaU00pYnJsxOMKAM9CiGNsBp80meTREkBTo9nTq245cH6fZ75Jfn8bfzfhjh7CH7vYd9J4HHfJa+uutr3Dw/ALY23CNW7334/2GFc7Thhmv8d+d8A5JXkcWTlkSHOlkfQ1+CxZqlPPdwiJslShFkasYzplb/6q4ITQ5v0DqPp8S4Z1FDo2qQ2fViLfwuhnktQB7jRYuSC+gsAWF0pxnF+dblUS1528jK0tuAawTxfMLQYSKiQBsoyt2UK0cx+IxuArL9kgbw1jQYlqAPcpDVRHlWODRuFiYVCNPek7MGOneL4YixqMXar4UZPbA+dSZ3YVXZqp8pYM28QGuc1YsdO88xmoVEZ9FXYBxkfMK1lGhVRAvqsgaPxR9mevt2xxqGCD6igdFUpsSdj6UoVs45g0+wmDLUG6i6sG/pkGSieTIXzkszMLE6cOKF4MhWGN997nsz8/AuE6G3f/hUAy5YtF6IH8O9/fw7A6tWXC9H78ENpqeHbb79DiB7AG2+8/u2WWN/os896vz76YDz4oDSq/eabfxai18/jjz8upgZXUDifUQJcIaRRAlwhpFECXCGkCdpEsIULCz0ahKfvnE5kp29eve2ztntMBDt3/1yfEsF+Pulzj4lgC44W+JQI9t0R73pM2rq6erVPSVsDYYxe17HOo0H4oYiHfDYIP1T1EE1W9xmNv0r7FaP1o33S7Oe8SAR7dtJWXZ//85ATmxOFaqa0pRDR63Tl9yej8pWM7gxX07GfBuFAMFHrahCOUPmWffpsphmnkax1mjyiNf57AIM+EWxqdapwg3B6bTrJzb6lnfbEqMZRpLWlCdMb2zmW0Sb/aq5AM1c3V7hBeFHkImZGiM3s8Z0lgs1tzWV59XI+Hfkpx6K8t1rVptfSFuf0ZWaXSZNy9BY9txXfxpGEI+xM3ynrGqtTq2mJcf7Mjj8hGSuXHFtCQncCX+R8QVOE9yaAysRKl0Swk09PBiCpLYmL9l9E4dhCjqV7/52PRR6j1uCc4zG3Za7Xn/VIAIzRu/p2UW4td5SvNFwJgLZdy5hXxtA0u4mm+fKMFNs6t1HSU+Io35xws9/X+Z0ngr2n7B5eGveSrESwLTiD8a3X33I5nt6ZzojOEchxBjbGN7qU17+y3rFtx864hnE8teQpr/XqYlznT7z24msu5cv2XsYXvV/gbUbJqnDXpK1+B3gAjNFHLK7zttc+6urDNZ4xYqwzIoeDpoMu5aAM8LG7x5Jdme0o/2ay9CYzpWUKBXUFbErfxMnIk17r5R7MJfN0pmNq67MzpVVKDVYDtxXfRkl8CVtGbYGmH3utmVecR3a18xr/d8H/ArC8bDlxpjg2j90sa6bh7PLZTKhxrhHy+lJpdDGlNYWlB5eyb8w+jmQcAS/dZpeeupSH33iY9bevH/pkbwiAMfp24+3kdeahskqDiYcfPQxI87qzX8+mJa+F2uW18I33mus2rCP75mz6MrxPKT4UwgPcprLRZHD/afoy7Uu+TP3SpxHlDr370mMAT8590ic9i9pCa7h7js13p327nIVcTRW0RbgvZ9YW0UZZepnQlBzBRF+ceyCaE80U/booaL7zdztdVvSXDna9QGkGO0H0nZWBHoWQJmgTwc7+Wkzmh7PJ35MvVG/5YXEzFwGuPXMtAJHt/i86CQTEGP2LqF/4/uEBeCbjGQBGl4ymmmqh2koNHmzY4YJt0hTiBV8t+J4v5rsj/g1ppdrEVxKHjydzWKIC7FJ3pcoeRI3ZQGOTvrMdu9A2vBLgQcje2XuxaC0cmHHg+76U74y2K9qwG+y03tCqJIINdepT63n71re/78v4TrEmWKl6qWroE2WimI4VzktycsZy7NgxxXSsMLyRXYNPmyZmsZyDB6X25XBMBPvQQ/9XkB4888zvAFi7dp0Qvccek7oBX3rpZSF6P/zhvQB89NHHQvT6+dnPfiamBldQOJ9RAlwhpFECXCGkEdZNeOSiI/RFeEgEu2UcxjZ584JheCaCfSXiFdrV7W77b+26lWSbbw6kZ23P0or7zMk1qjWkqeS7kB6tf5RmW7Pb/v9K+C8ydBk+XeOdRXdSb6532/987vNkh2d7+IT3iE8EW6MkgvWXbEs2sTZnrlGjXX4FcS7jGOeSuDUC/zyUU/RTSNIkOcqRav/nz8yOmU2a3vnQxWj9X8M9IIlgY2rELS4/HBPBTu6bzFjLWKGaM1UzyVXlCtNbaFzIdMN0YXoAyxOXMz92vlDNgCeCHVEkLSUQY44hpzOH/XH7sanOmU1jh9y2XFp1rdREuCaq8jURbFxPHBntGRxKOuTWyxfsiWCLdcWc1jhzZS7pXeLYTi1LpTOhk84E9+UlBmOvfS8n7Ccc5UvVlwJgaDIQWRNJ48RGWW9kX5u+psxc5ihfF32dtGGB6N3RdE3uwhotL1nt542fU9zhtD3dnXG3rM97Qnwi2DTXNuS7f3VN+np5zeW8MOYFR1lv1XPfkftI7nVtY96QfwN14XU+JYJdfmo5C6sXorPruL78eqfmnBuoM9YFfSLY49rjLuVnnnjGpWzVWDmTe4ZDKw55rVlGmUv5yceedCn3xPRw8C5XT+RgFPUWuZR/8R+u02htOhv117q3qwejsM01yUFQBvj0bdN55OtH0FuldnObVgrQGIvUbOnSdGFROQeL7NhpD2t3BHi7rt2xH+A/3/1PKs2VlMW43qDB6NJ1YVfZwQ7d2m6sKquL5g8+/QEV6grpHH8JgN9xdfdqVm5dSUax9NLWE+FcrMjQJb079EbIS5Z6e/PtXLf+OtQWqZo2R0ov8GGd0vtSX0Qfdo33/x5rItdw6fpLMZyUrscSLd1TbbsUUnatHWuEvBp83YZ15P04D1umuPmywgO8NayVJyY84bbfaDUywjSC8ohylyaDWWPm5fEvM7JrJJ3aTlr1rQ4dgHcz35XdBt+RvoN9yftI60rjRIzzZ7lNLz1su1J3BXUbHBWU5pdSml/qdijuTBzdsd2yA7wnoYfCB93TwOg6dRibjLSPdu+9GQy71s6ZH3lIRmuD8KPhmMaasIfZ4RVZssL5zroPTBoT5ZHlAx4/Nz+7v/Roe1yCO1RoGeG+bJo/9EX20RcpzsWOGroneZ/JOtAoAz0KIY2wGnziZxNFSQHiPZ7gTAQrhAD4He/u8v+l6lweVD8oVO+JZPfmp7+8NkVaKCny8Ui6EVv7KzW4QlCgKZISymr2iUks248S4ApBQdibUm9O2DthiulYIfQw3yx1W5qvMw+vRLAKwwPrDCumR01YZ8jrOx8KxZOpcF6SmzuRI0eOKJ5MheGN7Bp8wgQxuclLSo72qwrR6/c7il35UdK8994fClF7+eWXAHjkkUeF6AE8+aTUbff8838Qonf//fd9uyX2vuzZs1eQnsStt94qpgZXUDifUQJcIaRRAlwhpBHWTVi+qhxLhPuaKZn/ysTQKjMNXgD8joHQfCvpLY95La9uuJpES6JsvRfDXqRN5Z4p4g7zHaTYU+RfIPCrtl959FA+HPUwI7Uj5YkF4r4AqzavosZU47b/rQveYnyMfxPuhfeDR5yJcMwxBtD0ih16DUZG9Ywi2uq08xht/nkoc6w5xNqdnsxwu28m67OZpJtEotr50InwUIrmguQLGBnhfOjiwvy3KgoP8NjjsUSdkZ81+HxmQvcEsnr9cAWdwzTbNMbZxgnTA5gXNo+pYeInsInk8lGXszh1sVBNnwNca9N6zETWmt1Kd7JzRljKft9+WoGA+B0DoVkSXkK13pmZYGG7c/k4tUWNTStvcsVB9UFOqU45ysutzkwSaosam8Ymuxdvp3kn5RbnfPyrwq+SJ3A2gbgvwAeVH7C3ydmd+NCkh/zWlB3gcX1xXN5wOXPb5/JR4kfUhEltpypbFRYsdI3oogtnX7lfAR4Av2MgNCsNlS7l6w9IPtCE+gRyD+ZSMaGCotlFnj7qkXKNqzHk5sPOfJFTP5hKZ2InpctKaRntvfnhcN9hl7JfAR6I+wJ8Vf+VS/l7CfBZ7bOY0z4HgFWNqxz7t1i30EUX6zasY3PvZmr1tQNJeE8A/I6B0Lz6xNX85M8/GfD4mJIxNCV5n/X3avPVrHlqDRqL5/eXqIYoxm8ez847vM/w/MsPf8nYzLE0FcjLPuyRQNwXJE/miqdXoE4T17knO8A/j/+c0/rTLGlZwoaUDTSHSW/oTTrpH+6lES8NuzZ4R0wHG+7d4LY/qiWKGTtnUDKthPr0evjKw4c9oYLND2/2eGjyh5PpSOmgKk/eYvHabi3hleE0ISDAA4i9S4AR/Czkt8FVcDTyKEcjjw597jCnI66DbZdsE6pZvNrLdMkKgDLQoxDiCOsmzPkoR5RUQPyOgdC8ueHmoU+SwY/MPxKqB/DLmF8CMLVkKi2z/HTkB+K+AB8t/QiAjsc9p2z3B6UGHw5820upsgRvWkJ737dtb/cFhf1CCfBhQPK/pFXDYg/EEtYYNsTZ3w/da7od/7fbxL1oKgE+DOga14VNY6Mvqg9znOAqUhDa+VpQg2a2BpVa3C+N4skcBnTldNGa10r75HYI0qlBYTeEYd1rxfATmRPzhkAJ8GHC6VvELo0nGlWEivAX/Z9U5qarmI4VzkemT5/B/v37FdOxwvBGdg0+fry8zAIDUVraP5lBrLn1kksuFaQHn376CQDXXXf9EGd6x9///s63W+KN0f/4x3tC1K655upvt8Tel7Y2ecszD0VBQYGYGlxB4XxGCXCFkEYJcIWQRlg3YcWqCiyR7g6f0Z+ODg7TMfDl9C8x6U1u+xcWLSS6W7415eOcj+kOc1/PennFcuJ6ffATBuB7ryldQ0Ofe+fA02OeJsso02YXoPsy5bUpVLZXuu3/6uavmJrsn81uWJqOk1qSCO9x9rmG9fk3fJ3WkUak2Wni7U/AFUzMjJpJaliqoxytFeg1E8TFWReTFet86BLD5a9McC7CAzymIiboDQ8ZDRmktPhhpTuH7NZsRnSMEKYXCJbGLWVO9Jzv+zIG5dbJt7IyZ6VQTeEB3jamDVOKsxmQvM+3HOtAwMytVUlVNEU5nS0TK6X0K9NPTSeyN5LCrEJ6da5ZzGLbY8k7msfBcQdpinN1xRyPPU59uDMn5Iy6Gf5dYAC+9+aWzRzucvoyb0+73XexAN2XvxT/he2ntzvKv1nsY5vnLIQH+LmmY78CPEDm1oY41zbpmy+/6di2Y2fWyVn8z9L/cewbWTuSldtWokLF+FPOi9r6wFa6w7qpiXJdtMbvAA/A997b4br4pV8BHqD78q8T/3IpB2WAr9uwjvST6Tw1+in/xQJkbl10cBEFRwsc5S0TtgCwoHwBADvG7MCqdi7E3hTbRElmCbknc6lKqaIyVXoh6q/lb9x1IyqjCovW/SXbJwLwvddtWMfs5Nl03idgoC6ApuO7X78b4yT/Fk46m4BMtlIJHakTT6exkz1Z7nNq9o/ajwoVFo1roJoMJr6c8yU7pu/ArDM7BvnMOmnqaWV6ZdC3wYcrymzCs7BqBk+fYQ4LzrnUCgOjDPQohDTCavAxH40BIL80nxMGP1NoB8jcuvjAYv8EzmFludgurUB87z+O/yMACSUJ9CbLy2/vRoDuS9Gd0qpf+x7f55+QB4TW4Nnd2QBk9WQRZQnuvvDhhG6vDgD9Nj24D+QGBbW/l1ZCq/lNDXJmuA6F0AA/e03scJt4d4aCb2hqpNFku8qOyhScHQCdO6Tene793c50SwIQGuCFUYW0aFvYH7mfurA6kdIKftCzvAdbhI3eZb3Y48UujSaKEY+PABWMWDsieE3HdpWdtZlrsagE9QcriEGAGfszAAAFNUlEQVQPrS+0YtcHZ3ADGCcamVI6BW2S2I49xZOpcJ6iwm63K55MheGN7Bp86tQ+IX/40KGDAMyaNVuI3p49hQDk518gRA9g+/b+9Y7F+hM/+uhjQXqwapXUVVlUJGbV2SlTJgPiPJQxMf2zscS/3AqpwRUUzmeUAFcIaZQAVwhphPXJHF1xlL4I9/b52M1jMbbJn/546MJDmMPdJzdN3DaR8HbfBpEKFxbSa3Qfrp6+czqRnTLzRgbAn3hn0Z3Um+vd9j+f+zzZ4dnyBYEVn66gurvabf+7S99lQuwE2XoB8U+OAPKBDMAIdAP1SB12fiYSET6bMKomCn2X05Oo7fXvT8TUxbjqmf2/5LiGOIwm50On69P5rSmS2TGzSdOnOcox2hi/NQtSC8iIzHCU4/T+JVkV5p+cCFyD1JZoAMoAPVLQTyH4Ajz+ZDwxNf7fkH4SKxOJq/M/4+3ZpFanktCQIFRTJMsTlzM/dr5QzSszr2TpiKXC9IT4J3XASqTgLgLex7FYPyrAf8+x+ABvzmymK8lpWUs/lA6AzqYjpSeF0+HyVjltHNVIR4IztcWoI6Mc2yO7RlJrrPWYkFZn1ZFoSqQm0j0Hem16LW1xzpzw2WW+/fwDAfEnft74OcUdzm6/uzPudmyrT6qxJdpAZovq/ZPvs6fROUj382k/B8DWYcNWbUM7Xl4oDOSftNvtdO/pJnx6OCrdEL14GUB/a3MrzuAGqUdVwLCL8ADvSOugA2dAPv3e0wBkmjIBOBF+gjdHvem1XltKm0u5X89gNZDck0y3ppv3Rr/nMr6aV5vHJScuwWA1UBNR45g6UDK7hF5jLy1JLbTgzFfjV4AHwJ9Y2FboUr7v9/c5tjVlGux6O+YbzfRd7f2YxNbarS7le397LwCWIunfRjdPR9RT3s8APdc/edva2wDoq+mjr7oPbZKWUS+OYtCnPuKs7dZv/78MqT3ez+NeX5JHhAf4vC/m8eTWJwc8ntqTisHm/UJA43eNZ+2WtST3ejYvh9nCSOtOc9mX2pWK1iZ9tbQu5zGNXZpV98A/H+BA+AGPNb9sAuBPfDTrUZa8sARt4QC3xwrqY/I6wH4X/jtm/sdMR9mC63e3lFiwm7wf9Fu/ZD1Z12ZhqZd0unFdAMnaaqW3bIj5511nbUcDzUAlcAjwb70fB8IDvMZQw/1T73fbn9CbQG5HLrvid9Gn9r7msagtPD3labf9apua+Q3zKY0ppdHQCLW/dhz7ZMwn7EndQ2ZbJoVphdhV0o1r1UvVxKasTUHdBkcNPY/1eDyk/VyLbbQN2zibx+MDoZ2qJbHIvVHbV9aH5ZAFw+WGoZsUZ6GJ1DD1mHsU2kw2Gl5vIHZVLPpRevivQUSqkHpMwoELgA+QXjLbCd4AH4gmfRPb9duHPtFLbGobX6d8PeDx+oh66iPcu9zOdyzLxc7U1I3ToRsnrhdJbVST8mMvF1XqAz4BrkJ6l0kDTgPi+igU07HC90wxUo29EOmlcwZS06UcOOK/vLAAz92UK0oKgKlbBP1GncXsr8VM7AIC4k98bcprvn94ADZdskmoXr9/UiiV3/4XAJSheoWQRglwhZBGCXCFkEYJcIWQRglwhZBGpmVN1QGUCvz7iUBjEOsFQnM4XmMgvvNou92eNNRJcrsJS+12+ywfL8gNlUq1J5j1AqE5HK8xEN/ZW5QmikJIowS4QkgjN8D/JPjvB7teIDSH4zUG4jt7hayXTAWF8w2liaIQ0igBrhDSKAGuENIoAa4Q0igBrhDS/H9AqY0TJVHWJQAAAABJRU5ErkJggg==\n",
+      "text/plain": [
+       "<Figure size 216x216 with 1 Axes>"
+      ]
+     },
+     "metadata": {},
+     "output_type": "display_data"
+    }
+   ],
+   "source": [
+    "from IPython.display import clear_output\n",
+    "from time import sleep\n",
+    "mdp = FrozenLakeEnv(map_name='8x8',slip_chance=0.1)\n",
+    "state_values = {s : 0 for s in mdp.get_all_states()}\n",
+    "\n",
+    "for i in range(30):\n",
+    "    clear_output(True)\n",
+    "    print(\"after iteration %i\"%i)\n",
+    "    state_values = value_iteration(mdp, state_values, num_iter=1)\n",
+    "    draw_policy(mdp, state_values)\n",
+    "    sleep(0.5)\n",
+    "# please ignore iter 0 at each step"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "Massive tests"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 22,
+   "metadata": {},
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "iter    0   |   diff: 1.00000   |   V(start): 0.000 \n",
+      "iter    1   |   diff: 0.90000   |   V(start): 0.000 \n",
+      "iter    2   |   diff: 0.81000   |   V(start): 0.000 \n",
+      "iter    3   |   diff: 0.72900   |   V(start): 0.000 \n",
+      "iter    4   |   diff: 0.65610   |   V(start): 0.000 \n",
+      "iter    5   |   diff: 0.59049   |   V(start): 0.590 \n",
+      "iter    6   |   diff: 0.00000   |   V(start): 0.590 \n",
+      "Terminated\n",
+      "average reward:  1.0\n",
+      "Well done!\n"
+     ]
+    }
+   ],
+   "source": [
+    "mdp = FrozenLakeEnv(slip_chance=0)\n",
+    "state_values = value_iteration(mdp)\n",
+    "\n",
+    "total_rewards = []\n",
+    "for game_i in range(1000):\n",
+    "    s = mdp.reset()\n",
+    "    rewards = []\n",
+    "    for t in range(100):\n",
+    "        s, r, done, _ = mdp.step(get_optimal_action(mdp, state_values, s, gamma))\n",
+    "        rewards.append(r)\n",
+    "        if done: break\n",
+    "    total_rewards.append(np.sum(rewards))\n",
+    "    \n",
+    "print(\"average reward: \", np.mean(total_rewards))\n",
+    "assert(1.0 <= np.mean(total_rewards) <= 1.0)\n",
+    "print(\"Well done!\")"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 23,
+   "metadata": {},
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "iter    0   |   diff: 0.90000   |   V(start): 0.000 \n",
+      "iter    1   |   diff: 0.72900   |   V(start): 0.000 \n",
+      "iter    2   |   diff: 0.62330   |   V(start): 0.000 \n",
+      "iter    3   |   diff: 0.50487   |   V(start): 0.000 \n",
+      "iter    4   |   diff: 0.40894   |   V(start): 0.000 \n",
+      "iter    5   |   diff: 0.34868   |   V(start): 0.349 \n",
+      "iter    6   |   diff: 0.06529   |   V(start): 0.410 \n",
+      "iter    7   |   diff: 0.05832   |   V(start): 0.468 \n",
+      "iter    8   |   diff: 0.01139   |   V(start): 0.480 \n",
+      "iter    9   |   diff: 0.00764   |   V(start): 0.487 \n",
+      "iter   10   |   diff: 0.00164   |   V(start): 0.489 \n",
+      "iter   11   |   diff: 0.00094   |   V(start): 0.490 \n",
+      "iter   12   |   diff: 0.00022   |   V(start): 0.490 \n",
+      "iter   13   |   diff: 0.00011   |   V(start): 0.490 \n",
+      "iter   14   |   diff: 0.00003   |   V(start): 0.490 \n",
+      "iter   15   |   diff: 0.00001   |   V(start): 0.490 \n",
+      "iter   16   |   diff: 0.00000   |   V(start): 0.490 \n",
+      "Terminated\n",
+      "average reward:  0.891\n",
+      "Well done!\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Measure agent's average reward\n",
+    "mdp = FrozenLakeEnv(slip_chance=0.1)\n",
+    "state_values = value_iteration(mdp)\n",
+    "\n",
+    "total_rewards = []\n",
+    "for game_i in range(1000):\n",
+    "    s = mdp.reset()\n",
+    "    rewards = []\n",
+    "    for t in range(100):\n",
+    "        s, r, done, _ = mdp.step(get_optimal_action(mdp, state_values, s, gamma))\n",
+    "        rewards.append(r)\n",
+    "        if done: break\n",
+    "    total_rewards.append(np.sum(rewards))\n",
+    "    \n",
+    "print(\"average reward: \", np.mean(total_rewards))\n",
+    "assert(0.8 <= np.mean(total_rewards) <= 0.95)\n",
+    "print(\"Well done!\")"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 24,
+   "metadata": {},
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "iter    0   |   diff: 0.75000   |   V(start): 0.000 \n",
+      "iter    1   |   diff: 0.50625   |   V(start): 0.000 \n",
+      "iter    2   |   diff: 0.39867   |   V(start): 0.000 \n",
+      "iter    3   |   diff: 0.26910   |   V(start): 0.000 \n",
+      "iter    4   |   diff: 0.18164   |   V(start): 0.000 \n",
+      "iter    5   |   diff: 0.14013   |   V(start): 0.140 \n",
+      "iter    6   |   diff: 0.07028   |   V(start): 0.199 \n",
+      "iter    7   |   diff: 0.06030   |   V(start): 0.260 \n",
+      "iter    8   |   diff: 0.02594   |   V(start): 0.285 \n",
+      "iter    9   |   diff: 0.01918   |   V(start): 0.305 \n",
+      "iter   10   |   diff: 0.00858   |   V(start): 0.313 \n",
+      "iter   11   |   diff: 0.00560   |   V(start): 0.319 \n",
+      "iter   12   |   diff: 0.00260   |   V(start): 0.321 \n",
+      "iter   13   |   diff: 0.00159   |   V(start): 0.323 \n",
+      "iter   14   |   diff: 0.00076   |   V(start): 0.324 \n",
+      "iter   15   |   diff: 0.00045   |   V(start): 0.324 \n",
+      "iter   16   |   diff: 0.00022   |   V(start): 0.324 \n",
+      "iter   17   |   diff: 0.00012   |   V(start): 0.325 \n",
+      "iter   18   |   diff: 0.00006   |   V(start): 0.325 \n",
+      "iter   19   |   diff: 0.00003   |   V(start): 0.325 \n",
+      "iter   20   |   diff: 0.00002   |   V(start): 0.325 \n",
+      "iter   21   |   diff: 0.00001   |   V(start): 0.325 \n",
+      "Terminated\n",
+      "average reward:  0.655\n",
+      "Well done!\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Measure agent's average reward\n",
+    "mdp = FrozenLakeEnv(slip_chance=0.25)\n",
+    "state_values = value_iteration(mdp)\n",
+    "\n",
+    "total_rewards = []\n",
+    "for game_i in range(1000):\n",
+    "    s = mdp.reset()\n",
+    "    rewards = []\n",
+    "    for t in range(100):\n",
+    "        s, r, done, _ = mdp.step(get_optimal_action(mdp, state_values, s, gamma))\n",
+    "        rewards.append(r)\n",
+    "        if done: break\n",
+    "    total_rewards.append(np.sum(rewards))\n",
+    "    \n",
+    "print(\"average reward: \", np.mean(total_rewards))\n",
+    "assert(0.6 <= np.mean(total_rewards) <= 0.7)\n",
+    "print(\"Well done!\")"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 25,
+   "metadata": {},
+   "outputs": [
+    {
+     "name": "stdout",
+     "output_type": "stream",
+     "text": [
+      "iter    0   |   diff: 0.80000   |   V(start): 0.000 \n",
+      "iter    1   |   diff: 0.57600   |   V(start): 0.000 \n",
+      "iter    2   |   diff: 0.41472   |   V(start): 0.000 \n",
+      "iter    3   |   diff: 0.29860   |   V(start): 0.000 \n",
+      "iter    4   |   diff: 0.24186   |   V(start): 0.000 \n",
+      "iter    5   |   diff: 0.19349   |   V(start): 0.000 \n",
+      "iter    6   |   diff: 0.15325   |   V(start): 0.000 \n",
+      "iter    7   |   diff: 0.12288   |   V(start): 0.000 \n",
+      "iter    8   |   diff: 0.09930   |   V(start): 0.000 \n",
+      "iter    9   |   diff: 0.08037   |   V(start): 0.000 \n",
+      "iter   10   |   diff: 0.06426   |   V(start): 0.000 \n",
+      "iter   11   |   diff: 0.05129   |   V(start): 0.000 \n",
+      "iter   12   |   diff: 0.04330   |   V(start): 0.000 \n",
+      "iter   13   |   diff: 0.03802   |   V(start): 0.033 \n",
+      "iter   14   |   diff: 0.03332   |   V(start): 0.058 \n",
+      "iter   15   |   diff: 0.02910   |   V(start): 0.087 \n",
+      "iter   16   |   diff: 0.01855   |   V(start): 0.106 \n",
+      "iter   17   |   diff: 0.01403   |   V(start): 0.120 \n",
+      "iter   18   |   diff: 0.00810   |   V(start): 0.128 \n",
+      "iter   19   |   diff: 0.00555   |   V(start): 0.133 \n",
+      "iter   20   |   diff: 0.00321   |   V(start): 0.137 \n",
+      "iter   21   |   diff: 0.00247   |   V(start): 0.138 \n",
+      "iter   22   |   diff: 0.00147   |   V(start): 0.139 \n",
+      "iter   23   |   diff: 0.00104   |   V(start): 0.140 \n",
+      "iter   24   |   diff: 0.00058   |   V(start): 0.140 \n",
+      "iter   25   |   diff: 0.00036   |   V(start): 0.141 \n",
+      "iter   26   |   diff: 0.00024   |   V(start): 0.141 \n",
+      "iter   27   |   diff: 0.00018   |   V(start): 0.141 \n",
+      "iter   28   |   diff: 0.00012   |   V(start): 0.141 \n",
+      "iter   29   |   diff: 0.00007   |   V(start): 0.141 \n",
+      "iter   30   |   diff: 0.00004   |   V(start): 0.141 \n",
+      "iter   31   |   diff: 0.00003   |   V(start): 0.141 \n",
+      "iter   32   |   diff: 0.00001   |   V(start): 0.141 \n",
+      "iter   33   |   diff: 0.00001   |   V(start): 0.141 \n",
+      "Terminated\n",
+      "average reward:  0.758\n",
+      "Well done!\n"
+     ]
+    }
+   ],
+   "source": [
+    "# Measure agent's average reward\n",
+    "mdp = FrozenLakeEnv(slip_chance=0.2, map_name='8x8')\n",
+    "state_values = value_iteration(mdp)\n",
+    "\n",
+    "total_rewards = []\n",
+    "for game_i in range(1000):\n",
+    "    s = mdp.reset()\n",
+    "    rewards = []\n",
+    "    for t in range(100):\n",
+    "        s, r, done, _ = mdp.step(get_optimal_action(mdp, state_values, s, gamma))\n",
+    "        rewards.append(r)\n",
+    "        if done: break\n",
+    "    total_rewards.append(np.sum(rewards))\n",
+    "    \n",
+    "print(\"average reward: \", np.mean(total_rewards))\n",
+    "assert(0.6 <= np.mean(total_rewards) <= 0.8)\n",
+    "print(\"Well done!\")"
+   ]
+  },
+  {
+   "cell_type": "markdown",
+   "metadata": {},
+   "source": [
+    "### Submit to coursera"
+   ]
+  },
+  {
+   "cell_type": "code",
+   "execution_count": 26,
+   "metadata": {},
+   "outputs": [],
+   "source": [
+    "from submit import submit_assigment\n",
+    "submit_assigment(\n",
+    "    get_action_value, \n",
+    "    get_new_state_value, \n",
+    "    get_optimal_action, \n",
+    "    value_iteration, \n",
+    "    'jiadaizhao@gmail.com', \n",
+    "    '03wHO9B5hDF0OZZp')"
+   ]
+  }
+ ],
+ "metadata": {
+  "kernelspec": {
+   "display_name": "Python 3",
+   "language": "python",
+   "name": "python3"
+  },
+  "language_info": {
+   "codemirror_mode": {
+    "name": "ipython",
+    "version": 3
+   },
+   "file_extension": ".py",
+   "mimetype": "text/x-python",
+   "name": "python",
+   "nbconvert_exporter": "python",
+   "pygments_lexer": "ipython3",
+   "version": "3.6.5"
+  }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 2
+}
diff --git a/Practical Reinforcement Learning/Week2_model_based/submit.py b/Practical Reinforcement Learning/Week2_model_based/submit.py
new file mode 100644
index 0000000..b0ad092
--- /dev/null
+++ b/Practical Reinforcement Learning/Week2_model_based/submit.py	
@@ -0,0 +1,121 @@
+import sys
+import numpy as np
+sys.path.append("..")
+import grading
+
+from mdp import MDP, FrozenLakeEnv
+
+
+def submit_assigment(
+        get_action_value,
+        get_new_state_value,
+        get_optimal_action,
+        value_iteration,
+        email,
+        token):
+    grader = grading.Grader("EheZDOgLEeenIA4g5qPHFA")
+    sys.stdout = None
+
+    transition_probs = {
+        's0': {
+            'a0': {'s1': 0.8, 's2': 0.2},
+            'a1': {'s1': 0.2, 's2': 0.8},
+        },
+        's1': {
+            'a0': {'s0': 0.2, 's2': 0.8},
+            'a1': {'s0': 0.8, 's2': 0.2},
+        },
+        's2': {
+            'a0': {'s3': 0.5, 's4': 0.5},
+            'a1': {'s3': 1.0},
+        },
+        's3': {
+            'a0': {'s1': 0.9, 's2': 0.1},
+            'a1': {'s1': 0.7, 's2': 0.3},
+        },
+        's4': {
+            'a0': {'s3': 1.0},
+            'a1': {'s3': 0.7, 's1': 0.3},
+        }
+    }
+    rewards = {
+        's0': {'a0': {'s1': 0, 's2': 1}, 'a1': {'s1': 0, 's2': 1}},
+        's1': {'a0': {'s0': -1, 's2': 1}, 'a1': {'s0': -1, 's2': 1}},
+        's2': {'a0': {'s3': 0, 's4': 1}, 'a1': {'s3': 0, 's4': 1}},
+        's3': {'a0': {'s1': -3, 's2': -3}, 'a1': {'s1': -3, 's2': -3}},
+        's4': {'a1': {'s1': +10}}
+    }
+
+    mdp = MDP(transition_probs, rewards, initial_state='s0')
+
+    test_Vs = {s: i for i, s in enumerate(mdp.get_all_states())}
+    qvalue1 = get_action_value(mdp, test_Vs, 's1', 'a0', 0.9)
+    qvalue2 = get_action_value(mdp, test_Vs, 's4', 'a1', 0.9)
+
+    grader.set_answer("F16dC", qvalue1 + qvalue2)
+
+    # ---
+
+    svalue1 = get_new_state_value(mdp, test_Vs, 's2', 0.9)
+    svalue2 = get_new_state_value(mdp, test_Vs, 's4', 0.9)
+
+    grader.set_answer("72cBp", svalue1 + svalue2)
+
+    # ---
+
+    state_values = {s: 0 for s in mdp.get_all_states()}
+    gamma = 0.9
+
+    # ---
+
+    action1 = get_optimal_action(mdp, state_values, 's1', gamma)
+    action2 = get_optimal_action(mdp, state_values, 's2', gamma)
+
+    grader.set_answer("xIuti", action1 + action2)
+
+    # ---
+
+    s = mdp.reset()
+    rewards = []
+    for _ in range(10000):
+        s, r, done, _ = mdp.step(get_optimal_action(mdp, state_values, s, gamma))
+        rewards.append(r)
+
+    grader.set_answer("Y8g0j", np.mean(rewards) + np.std(rewards))
+
+    mdp = FrozenLakeEnv(slip_chance=0.25)
+    state_values = value_iteration(mdp)
+    gamma = 0.9
+
+    total_rewards = []
+    for game_i in range(1000):
+        s = mdp.reset()
+        rewards = []
+        for t in range(100):
+            s, r, done, _ = mdp.step(get_optimal_action(mdp, state_values, s, gamma))
+            rewards.append(r)
+            if done: break
+        total_rewards.append(np.sum(rewards))
+
+    grader.set_answer("ABf1b", np.mean(total_rewards) + np.std(total_rewards))
+
+    # ---
+
+    mdp = FrozenLakeEnv(slip_chance=0.25, map_name='8x8')
+    state_values = value_iteration(mdp)
+    gamma = 0.9
+
+    total_rewards = []
+    for game_i in range(1000):
+        s = mdp.reset()
+        rewards = []
+        for t in range(100):
+            s, r, done, _ = mdp.step(get_optimal_action(mdp, state_values, s, gamma))
+            rewards.append(r)
+            if done: break
+        total_rewards.append(np.sum(rewards))
+
+    grader.set_answer("U3RzE", np.mean(total_rewards) + np.std(total_rewards))
+
+    sys.stdout = sys.__stdout__
+    grader.submit(email, token)