https://leetcode-cn.com/problems/decode-string/
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
示例:
s = "3[a]2[bc]", 返回 "aaabcbc".
s = "3[a2[c]]", 返回 "accaccacc".
s = "2[abc]3[cd]ef", 返回 "abcabccdcdcdef".
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/decode-string
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
n[string] 表示解析 [] 模板里面的内容,然后重复 n 次,即得到 n 个 string 拼接起来的字符串。
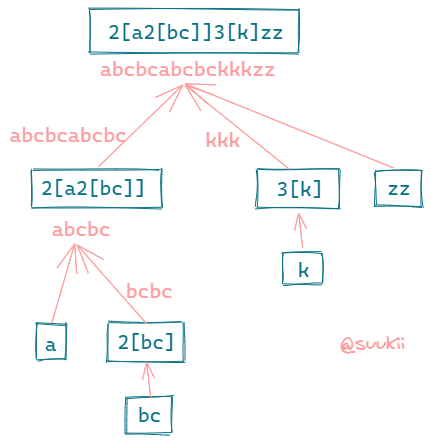
根据题意,[] 里面也是可以嵌套 [] 的,例如 n[m[string]]。这种情况下,我们得先解析最内层的模板,重复 m 次,然后将 m * string 的结果作为外层模板的解析内容,再重复 n 次。
如果嵌套的层数更多,我们也是得先找到最内层的 [],就像洋葱一样,一层一层地剥开,然后再从内到外一层一层地解析和拼接。这种描述很容易就让人想到了递归。
看代码注释吧。
- 时间复杂度:$O(S)$,S 是解析后字符串的长度。
- 空间复杂度:$O(S)$,S 是解析后字符串的长度,递归栈空间。
const type = {
isAlpha: s => /[a-z]/i.test(s),
isDigit: s => /[0-9]/.test(s),
isOpenParen: s => s === '[',
isCloseParen: s => s === ']',
};
/**
* @param {string} s
* @return {string}
*/
var decodeString = function (s, i = 0) {
// 从 i 开始遍历字符串
let decoded = ''; // 解密字符串
let cnt = ''; // 累计次数
while (i < s.length) {
if (type.isAlpha(s[i])) {
// 普通字符,直接拼接到 decoded
decoded += s[i];
i++;
} else if (type.isDigit(s[i])) {
// 数字,拼接到 cnt
cnt += s[i];
i++;
} else if (type.isOpenParen(s[i])) {
// 遇到开括号,就把括号内的字符串重复 cnt 次,再拼接到 decoded
// 但括号内可能存在嵌套括号,所以需要递归处理
// 我们需要从递归中取两个东西,1.括号内解析后的模式,2.这个开括号对应的右括号的下标,下次遍历字符串就从这个下标+1开始
const [pattern, nextIndex] = decodeString(s, i + 1);
// 重复 cnt 次拼接到 decoded
decoded += pattern.repeat(Number(cnt));
cnt = '';
i = nextIndex;
continue;
} else if (type.isCloseParen(s[i])) {
// 遇到闭括号,说明括号内的模式解析完毕
// 递归结束,返回我们需要的东西:1.解析后的字符串,2.解析到的字符下标
return [decoded, i + 1];
}
}
return decoded;
};C++ Code
class Solution {
private:
int ptr_ = 0;
public:
string decodeString(string s) {
string decoded_str = "";
string repeat_times = "";
int i = ptr_;
while (i < s.length()) {
if (isalpha(s[i])) {
decoded_str += s[i];
i++;
} else if (isdigit(s[i])) {
repeat_times += s[i];
i++;
} else if (s.compare(i, 1, "[") == 0) {
ptr_ = i + 1;
string pattern = decodeString(s);
i = ptr_;
int times = stoi(repeat_times);
for (int t = 0; t < times; t++) {
decoded_str += pattern;
}
repeat_times = "";
} else if (s.compare(i, 1, "]") == 0) {
ptr_ = i + 1;
return decoded_str;
}
}
return decoded_str;
}
};可以用递归解决的问题,也可以用循环来解决。
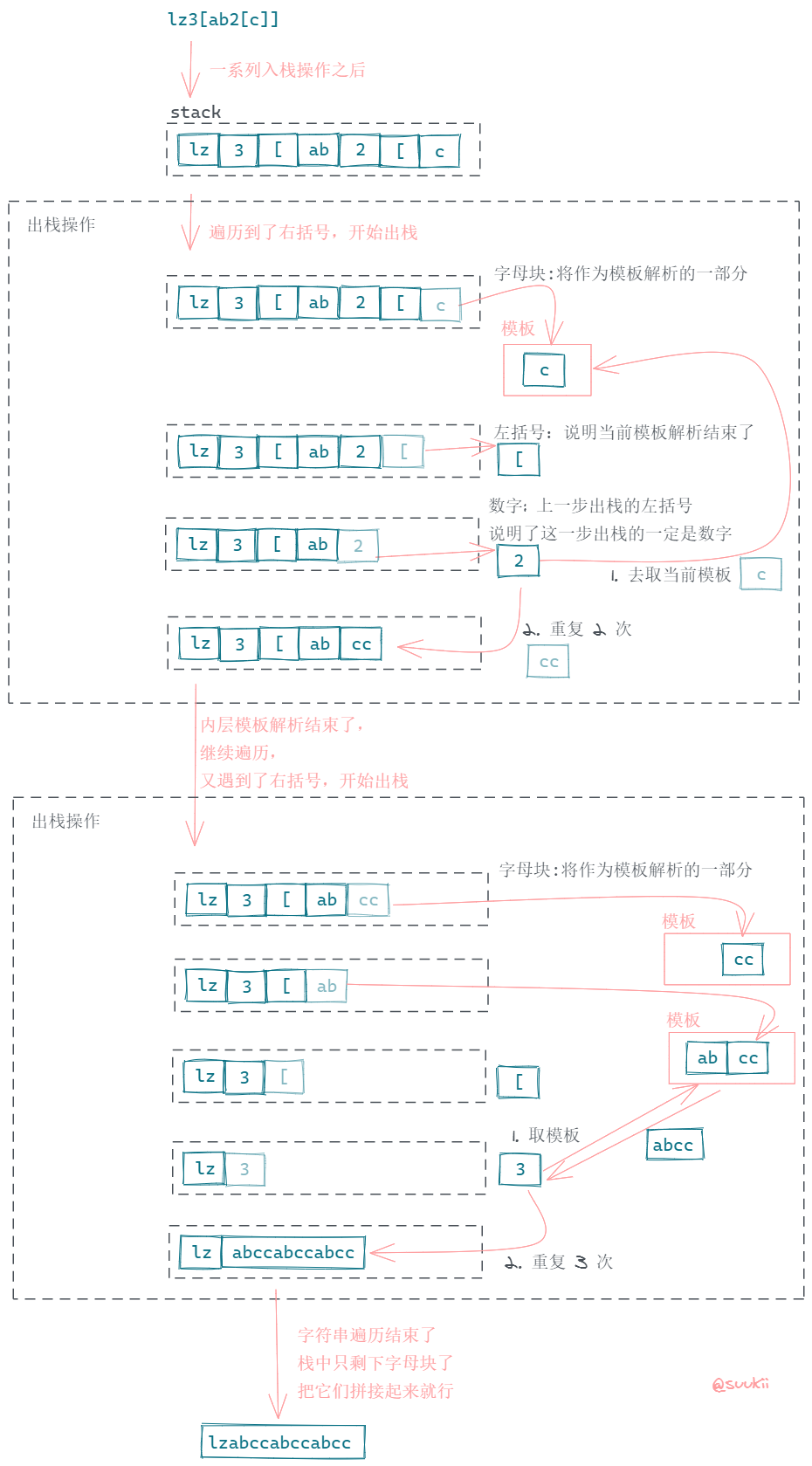
这里我用了正则 /[a-zA-Z]+|[0-9]+|\[|\]/ 和 exec() 方法来遍历字符串并把它们拆分成 token,比如,lz3[ab2[c]] 会被拆分成 lz, 3, [, ab, 2, [, c, ], ]。
- 遇到字母块 (
lz)、数字时,入栈; - 遇到
[时,入栈,用来标识当前进入一个模板解析了; - 遇到
]时,说明当前模板遍历完了,我们可以开始解析了。开始出栈,把出栈的字母块都拼接起来,等出栈到[时,说明当前模板解析完成了。继续出栈一个元素,这个元素就是当前模板要重复的次数,把"字母块 * 次数"后推入栈中。之所以要推入栈中是因为模板是可以嵌套的,当前模板的外层可以还是一个模板,所以我们要把结果放回去,继续解析外层的模板。
- 时间复杂度:$O(S)$,S 是解析后字符串的长度。
- 空间复杂度:$O(S)$,S 是解析后字符串的长度。
/**
* @param {string} s
* @return {string}
*/
var decodeString = function (s) {
const reg = /[a-zA-Z]+|[0-9]+|\[|\]/g;
const stack = [];
const peek = () => stack[stack.length - 1]; // p.s. 不正经栈
while (reg.lastIndex < s.length) {
let token = reg.exec(s)[0];
if (token !== ']') {
// 数字,字母,左括号通通入栈
stack.push(token);
} else {
// 遇到右括号就开始出栈
let str = '';
// [] 中间的就是要重复的模式,把它们全部出栈,拼接起来
while (peek() !== '[') {
str = stack.pop() + str;
}
// 丢掉左括号
stack.pop();
// 左括号前面的一定是模式重复的次数
const num = +stack.pop();
// 把复制操作后的字符串放回栈中,作为外层 [] 模式的一部分
stack.push(str.repeat(num));
}
}
return stack.join('');
};