有一个二维矩阵 grid ,每个位置要么是陆地(记号为 0 )要么是水域(记号为 1 )。
我们从一块陆地出发,每次可以往上下左右 4 个方向相邻区域走,能走到的所有陆地区域,我们将其称为一座「岛屿」。
如果一座岛屿 完全 由水域包围,即陆地边缘上下左右所有相邻区域都是水域,那么我们将其称为 「封闭岛屿」。
请返回封闭岛屿的数目。
示例 1:
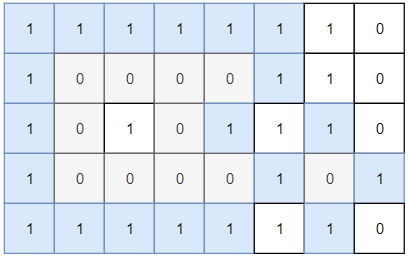
输入:grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]] 输出:2 解释: 灰色区域的岛屿是封闭岛屿,因为这座岛屿完全被水域包围(即被 1 区域包围)。
示例 2:
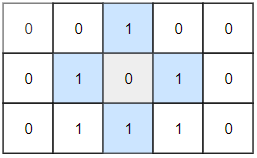
输入:grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]] 输出:1
示例 3:
输入:grid = [[1,1,1,1,1,1,1],
[1,0,0,0,0,0,1],
[1,0,1,1,1,0,1],
[1,0,1,0,1,0,1],
[1,0,1,1,1,0,1],
[1,0,0,0,0,0,1],
[1,1,1,1,1,1,1]]
输出:2
提示:
1 <= grid.length, grid[0].length <= 1000 <= grid[i][j] <=1
题目标签:Depth-first Search
题目链接:LeetCode / LeetCode中国
【并查集】
建立一个容量为m*n+2的并查集,0设为与边缘连通的0,m*n+1设为1,网格上坐标为(i, j)的点设为m*i+j+1。
使用并查集解本题有不少细节需要注意:
1、初始化时:如果边缘的点值为0,那么与0连通;如果边缘的点值为1,那么与m*n+1连通。4个边缘,8种情况,都需要进行相应的初始化。
2、join时,改变当前位置的父节点,而不是把其它位置的父节点设为当前位置。或者说,join时需要注意参数的次序。
3、在搜索中间位置时,如果网格上的点的值为0,只需要看左边的格子和上边的格子。
4、在搜素中间位置时,由于3,需要搜索最后一行和最后一列。
5、如果当前位置与边缘0连通,并且左边或上边的格子的值为0,那么,要改变左边或上边格子的父节点为0,而不是使用2的规则。
| Language | Runtime | Memory |
|---|---|---|
| cpp | 16 ms | 11.4 MB |
class UF {
private:
public:
vector<int> fa;
UF (int n) {
for (int i = 0; i < n; i++) {
fa.push_back(i);
}
}
int find(int x) {
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
void join(int x, int y) {
fa[find(x)] = find(y);
}
};
class Solution {
public:
void printUF(UF& uf, int n, int m) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cout << uf.fa[m * i + j + 1] << "\t";
}
cout << endl;
}
cout << "-----" << endl;
}
int closedIsland(vector<vector<int>>& grid) {
int n = grid.size();
int m = grid[0].size();
if (n < 3 || m < 3) return 0;
UF edge(n * m + 2);
for (int i = 0; i < n; i++) {
if (!grid[i][0]) {
edge.join(m * i + 1, 0);
} else {
edge.join(m * i + 1, m * n + 1);
}
if (!grid[i][m - 1]) {
edge.join(m * (i + 1), 0);
} else {
edge.join(m * (i + 1), m * n + 1);
}
}
for (int i = 0; i < m; i++) {
if (!grid[0][i]) {
edge.join(i + 1, 0);
} else {
edge.join(i + 1, m * n + 1);
}
if (!grid[n - 1][i]) {
edge.join(m * (n - 1) + i + 1, 0);
} else {
edge.join(m * (n - 1) + i + 1, m * n + 1);
}
}
for (int i = 1; i < n; i++) {
for (int j = 1; j < m; j++) {
if (!grid[i][j]) {
if (!grid[i - 1][j]) {
if (edge.find(m * i + j + 1) == 0) {
edge.join(m * (i - 1) + j + 1, 0);
} else {
edge.join(m * i + j + 1, m * (i - 1) + j + 1);
}
}
if (!grid[i][j - 1]) {
if (edge.find(m * i + j + 1) == 0) {
edge.join(m * i + j, 0);
} else {
edge.join(m * i + j + 1, m * i + j);
}
}
} else {
edge.join(m * i + j + 1, m * n + 1);
}
}
}
unordered_set<int> fas;
int t;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if ((t = edge.find(m * i + j + 1)) != 0 && t != m * n + 1) {
fas.insert(t);
}
}
}
// printUF(edge, n, m);
return fas.size();
}
};【DFS】
考虑漫水填充的思路,对每一个0位置,使用DFS,如果访问到了边缘,那么不是封闭的岛屿。
注意,要记录哪些位置已访问。
| Language | Runtime | Memory |
|---|---|---|
| cpp | 8 ms | 10.3 MB |
int dx[] = {-1, 1, 0, 0};
int dy[] = {0, 0, 1, -1};
class Solution {
public:
void dfs(vector<vector<int>>& grid, int n, int m, int x, int y, vector<vector<int>>& vt, bool& flag) {
vt[x][y] = 1;
// 如果触达边缘,则未封闭
if (x == 0 || x == n - 1 || y == 0 || y == m - 1) {
flag = false;
}
for (int k = 0; k < 4; k++) {
int nx = x + dx[k];
int ny = y + dy[k];
// 未越界,可访问且还未访问
if (nx >= 0 && nx < n && ny >= 0 && ny < m && !grid[nx][ny] && !vt[nx][ny]) {
dfs(grid, n, m, nx, ny, vt, flag);
}
}
}
int closedIsland(vector<vector<int>>& grid) {
int n = grid.size();
int m = grid[0].size();
vector<vector<int>> vt(n, vector<int>(m));
int res = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
// 可访问且还未访问
if (!grid[i][j] && !vt[i][j]) {
bool flag = true;
dfs(grid, n, m, i, j, vt, flag);
if (flag) res++;
}
}
}
return res;
}
};