参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
题目描述
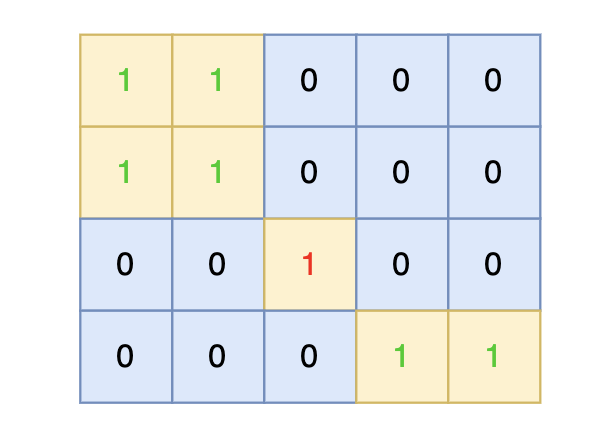
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域,且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。
现在你需要计算所有孤岛的总面积,岛屿面积的计算方式为组成岛屿的陆地的总数。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0。
输出描述
输出一个整数,表示所有孤岛的总面积,如果不存在孤岛,则输出 0。
输入示例
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例:
1
提示信息:
在矩阵中心部分的岛屿,因为没有任何一个单元格接触到矩阵边缘,所以该岛屿属于孤岛,总面积为 1。
数据范围:
1 <= M, N <= 50。
本题使用dfs,bfs,并查集都是可以的。
本题要求找到不靠边的陆地面积,那么我们只要从周边找到陆地然后 通过 dfs或者bfs 将周边靠陆地且相邻的陆地都变成海洋,然后再去重新遍历地图 统计此时还剩下的陆地就可以了。
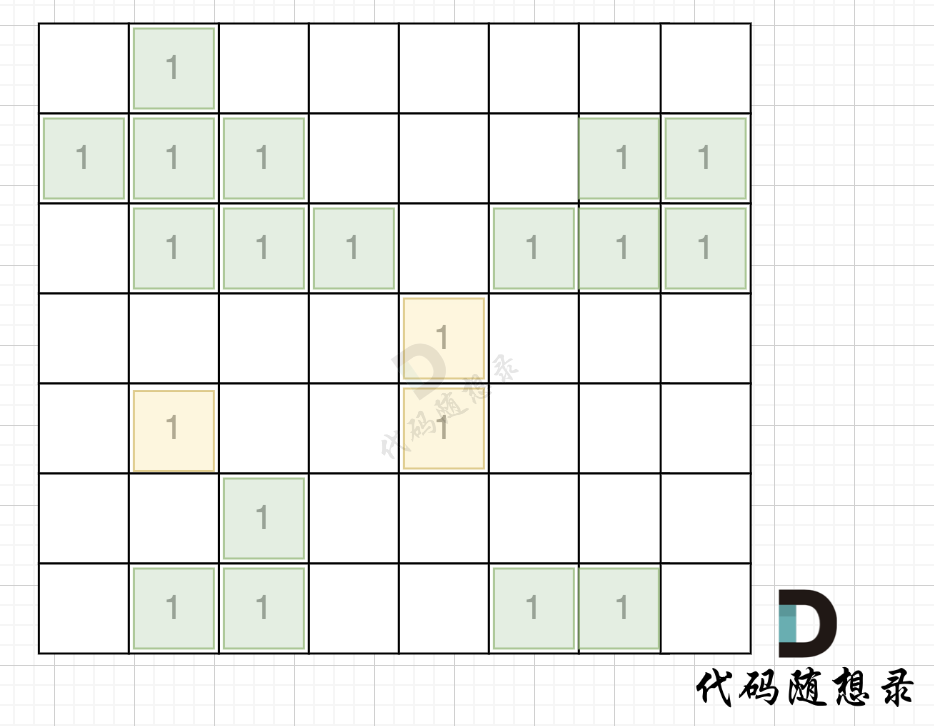
如图,在遍历地图周围四个边,靠地图四边的陆地,都为绿色,
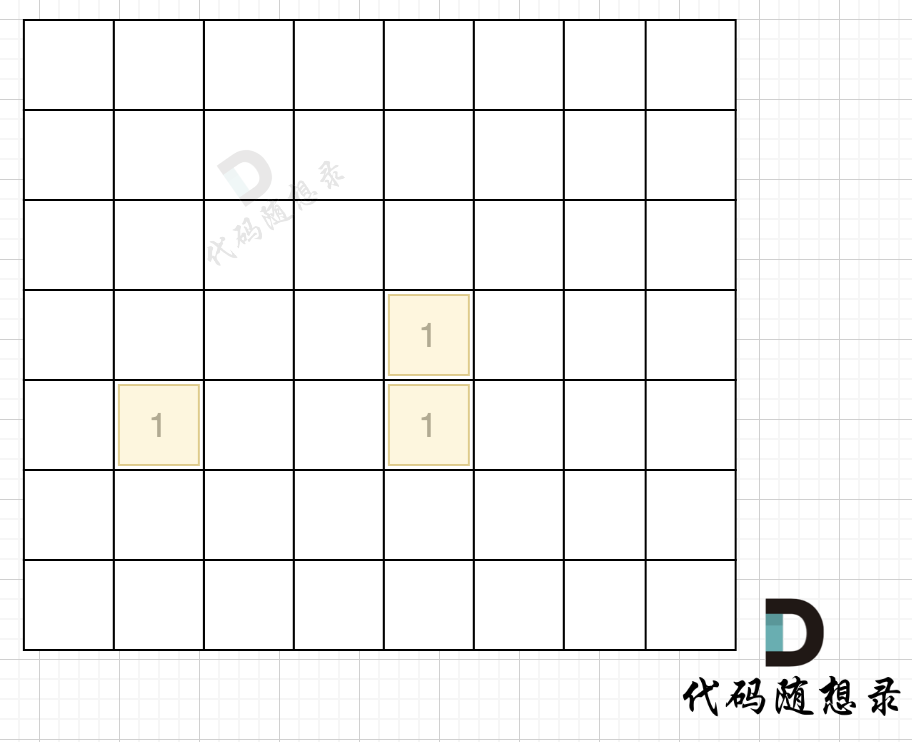
在遇到地图周边陆地的时候,将1都变为0,此时地图为这样:
然后我们再去遍历这个地图,遇到有陆地的地方,去采用深搜或者广搜,边统计所有陆地。
如果对深搜或者广搜不够了解,建议先看这里:深度优先搜索精讲,广度优先搜索精讲。
采用深度优先搜索的代码如下:
#include <iostream>
#include <vector>
using namespace std;
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1}; // 保存四个方向
int count; // 统计符合题目要求的陆地空格数量
void dfs(vector<vector<int>>& grid, int x, int y) {
grid[x][y] = 0;
count++;
for (int i = 0; i < 4; i++) { // 向四个方向遍历
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
// 超过边界
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
// 不符合条件,不继续遍历
if (grid[nextx][nexty] == 0) continue;
dfs (grid, nextx, nexty);
}
return;
}
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
// 从左侧边,和右侧边 向中间遍历
for (int i = 0; i < n; i++) {
if (grid[i][0] == 1) dfs(grid, i, 0);
if (grid[i][m - 1] == 1) dfs(grid, i, m - 1);
}
// 从上边和下边 向中间遍历
for (int j = 0; j < m; j++) {
if (grid[0][j] == 1) dfs(grid, 0, j);
if (grid[n - 1][j] == 1) dfs(grid, n - 1, j);
}
count = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 1) dfs(grid, i, j);
}
}
cout << count << endl;
}采用广度优先搜索的代码如下:
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int count = 0;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<int>>& grid, int x, int y) {
queue<pair<int, int>> que;
que.push({x, y});
grid[x][y] = 0; // 只要加入队列,立刻标记
count++;
while(!que.empty()) {
pair<int ,int> cur = que.front(); que.pop();
int curx = cur.first;
int cury = cur.second;
for (int i = 0; i < 4; i++) {
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
if (grid[nextx][nexty] == 1) {
que.push({nextx, nexty});
count++;
grid[nextx][nexty] = 0; // 只要加入队列立刻标记
}
}
}
}
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
// 从左侧边,和右侧边 向中间遍历
for (int i = 0; i < n; i++) {
if (grid[i][0] == 1) bfs(grid, i, 0);
if (grid[i][m - 1] == 1) bfs(grid, i, m - 1);
}
// 从上边和下边 向中间遍历
for (int j = 0; j < m; j++) {
if (grid[0][j] == 1) bfs(grid, 0, j);
if (grid[n - 1][j] == 1) bfs(grid, n - 1, j);
}
count = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 1) bfs(grid, i, j);
}
}
cout << count << endl;
}from collections import deque
# 处理输入
n, m = list(map(int, input().strip().split()))
g = []
for _ in range(n):
row = list(map(int, input().strip().split()))
g.append(row)
# 定义四个方向、孤岛面积(遍历完边缘后会被重置)
directions = [[0,1], [1,0], [-1,0], [0,-1]]
count = 0
# 广搜
def bfs(r, c):
global count
q = deque()
q.append((r, c))
g[r][c] = 0
count += 1
while q:
r, c = q.popleft()
for di in directions:
next_r = r + di[0]
next_c = c + di[1]
if next_c < 0 or next_c >= m or next_r < 0 or next_r >= n:
continue
if g[next_r][next_c] == 1:
q.append((next_r, next_c))
g[next_r][next_c] = 0
count += 1
for i in range(n):
if g[i][0] == 1: bfs(i, 0)
if g[i][m-1] == 1: bfs(i, m-1)
for i in range(m):
if g[0][i] == 1: bfs(0, i)
if g[n-1][i] == 1: bfs(n-1, i)
count = 0
for i in range(n):
for j in range(m):
if g[i][j] == 1: bfs(i, j)
print(count)