参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
题目描述:
给定一个由 1(陆地)和 0(水)组成的矩阵,你需要计算岛屿的数量。岛屿由水平方向或垂直方向上相邻的陆地连接而成,并且四周都是水域。你可以假设矩阵外均被水包围。
输入描述:
第一行包含两个整数 N, M,表示矩阵的行数和列数。
后续 N 行,每行包含 M 个数字,数字为 1 或者 0。
输出描述:
输出一个整数,表示岛屿的数量。如果不存在岛屿,则输出 0。
输入示例:
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例:
3
提示信息
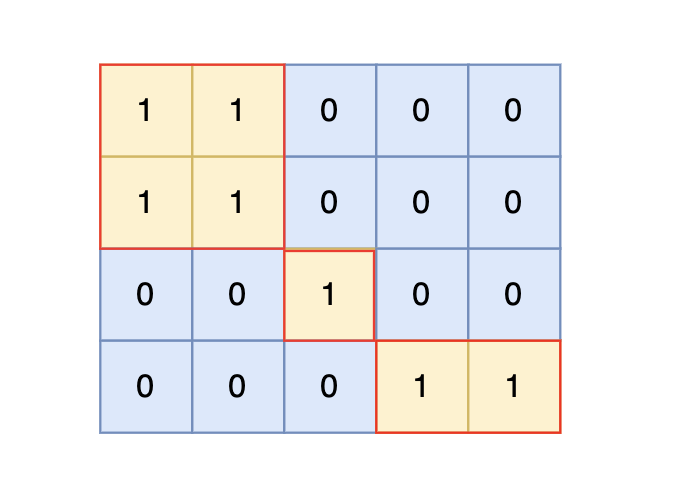
根据测试案例中所展示,岛屿数量共有 3 个,所以输出 3。
数据范围:
- 1 <= N, M <= 50
注意题目中每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
这道题题目是 DFS,BFS,并查集,基础题目。
本题思路,是用遇到一个没有遍历过的节点陆地,计数器就加一,然后把该节点陆地所能遍历到的陆地都标记上。
在遇到标记过的陆地节点和海洋节点的时候直接跳过。 这样计数器就是最终岛屿的数量。
那么如何把节点陆地所能遍历到的陆地都标记上呢,就可以使用 DFS,BFS或者并查集。
以下代码使用dfs实现,如果对dfs不太了解的话,建议按照代码随想录的讲解顺序学习。
C++代码如下:
// 版本一
#include <iostream>
#include <vector>
using namespace std;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void dfs(const vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
if (!visited[nextx][nexty] && grid[nextx][nexty] == 1) { // 没有访问过的 同时 是陆地的
visited[nextx][nexty] = true;
dfs(grid, visited, nextx, nexty);
}
}
}
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
vector<vector<bool>> visited(n, vector<bool>(m, false));
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (!visited[i][j] && grid[i][j] == 1) {
visited[i][j] = true;
result++; // 遇到没访问过的陆地,+1
dfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
}
}
}
cout << result << endl;
}很多录友可能有疑惑,为什么 以上代码中的dfs函数,没有终止条件呢? 感觉递归没有终止很危险。
其实终止条件 就写在了 调用dfs的地方,如果遇到不合法的方向,直接不会去调用dfs。
当然也可以这么写:
// 版本二
#include <iostream>
#include <vector>
using namespace std;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void dfs(const vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
if (visited[x][y] || grid[x][y] == 0) return; // 终止条件:访问过的节点 或者 遇到海水
visited[x][y] = true; // 标记访问过
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
dfs(grid, visited, nextx, nexty);
}
}
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
vector<vector<bool>> visited(n, vector<bool>(m, false));
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (!visited[i][j] && grid[i][j] == 1) {
result++; // 遇到没访问过的陆地,+1
dfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
}
}
}
cout << result << endl;
}这里大家应该能看出区别了,无疑就是版本一中 调用dfs 的条件判断 放在了 版本二 的 终止条件位置上。
版本一的写法是 :下一个节点是否能合法已经判断完了,传进dfs函数的就是合法节点。
版本二的写法是:不管节点是否合法,上来就dfs,然后在终止条件的地方进行判断,不合法再return。
理论上来讲,版本一的效率更高一些,因为避免了 没有意义的递归调用,在调用dfs之前,就做合法性判断。 但从写法来说,可能版本二 更利于理解一些。(不过其实都差不太多)
很多同学看了同一道题目,都是dfs,写法却不一样,有时候有终止条件,有时候连终止条件都没有,其实这就是根本原因,两种写法而已。
其实本题是 dfs,bfs 模板题,但正是因为是模板题,所以大家或者一些题解把重要的细节都很忽略了,我这里把大家没注意的但以后会踩的坑 都给列出来了。
本篇我只给出的dfs的写法,大家发现我写的还是比较细的,那么后面我再单独给出本题的bfs写法,虽然是模板题,但依然有很多注意的点,敬请期待!