1123

1123. Lowest Common Ancestor of Deepest Leaves (Medium)

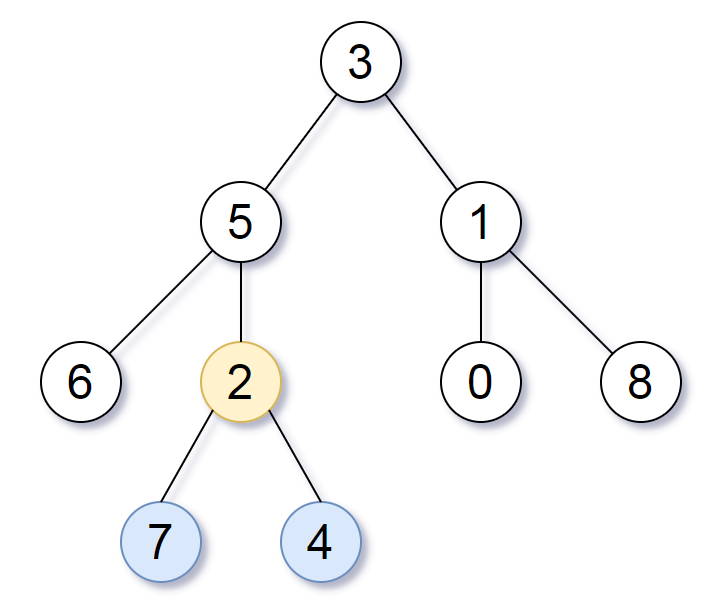
Given the root of a binary tree, return the lowest common ancestor of its deepest leaves.

Recall that:

• The node of a binary tree is a leaf if and only if it has no children
• The depth of the root of the tree is 0. if the depth of a node is d, the depth of each of its children is d + 1.
• The lowest common ancestor of a set S of nodes, is the node A with the largest depth such that every node in S is in the subtree with root A.

 

Example 1:

Input: root = [3,5,1,6,2,0,8,null,null,7,4]
Output: [2,7,4]
Explanation: We return the node with value 2, colored in yellow in the diagram.
The nodes coloured in blue are the deepest leaf-nodes of the tree.
Note that nodes 6, 0, and 8 are also leaf nodes, but the depth of them is 2, but the depth of nodes 7 and 4 is 3.

Example 2:

Input: root = [1]
Output: [1]
Explanation: The root is the deepest node in the tree, and it's the lca of itself.

Example 3:

Input: root = [0,1,3,null,2]
Output: [2]
Explanation: The deepest leaf node in the tree is 2, the lca of one node is itself.

 

Constraints:

• The number of nodes in the tree will be in the range [1, 1000].
• 0 <= Node.val <= 1000
• The values of the nodes in the tree are unique.

 

Note: This question is the same as 865: https://leetcode.com/problems/smallest-subtree-with-all-the-deepest-nodes/

Companies:
Facebook, Microsoft

Related Topics:
Hash Table, Tree, Depth-First Search, Breadth-First Search, Binary Tree

Similar Questions:

• Lowest Common Ancestor of a Binary Tree IV (Medium)

Solution 1.

// OJ: https://leetcode.com/problems/lowest-common-ancestor-of-deepest-leaves/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(H)
class Solution {
    int maxDepth = -1, target = 0, cnt = 0;
    void count(TreeNode *root, int d) {
        if (!root) return;
        if (d > maxDepth) {
            target = 1;
            maxDepth = d;
        } else if (d == maxDepth) ++target;
        count(root->left, d + 1);
        count(root->right, d + 1);
    }
    TreeNode *find(TreeNode *root, int d) {
        if (!root) return NULL;
        int before = cnt;
        auto left = find(root->left, d + 1);
        if (left) return left;
        auto right = find(root->right, d + 1);
        if (right) return right;
        if (d == maxDepth) ++cnt;
        return before == 0 && cnt == target ? root : NULL;
    }
public:
    TreeNode* lcaDeepestLeaves(TreeNode* root) {
        count(root, 0);
        return find(root, 0);
    }
};

Solution 2.

The lowest ancester is the highest node whose left and right subtrees have the same height.

// OJ: https://leetcode.com/problems/lowest-common-ancestor-of-deepest-leaves/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(H)
class Solution {
    pair<TreeNode*, int> dfs(TreeNode *root, int d = 0) { // latest node which has equal depth in left and right sub-trees; the corresponding height
        if (!root) return {nullptr, d};
        const auto &[left, ld] = dfs(root->left, d + 1);
        const auto &[right, rd] = dfs(root->right, d + 1);
        if (ld > rd) return {left, ld};
        if (ld < rd) return {right, rd};
        return {root, ld};
    }
public:
    TreeNode* lcaDeepestLeaves(TreeNode* root) {
        return dfs(root).first;
    }
};