You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
Hi Professor Lu, thanks for the well-written codes. I am reading the advection data generation code, case 3, where the input function is defined to be a square wave plus a continuous bump, the following are your parameter setting:
Thus, the c2 + a / h2 could be bigger than 1. In pde.solve code, seems like this case is never handled, and because of the periodic boundary condition assumption, the current implementation may have the following inputs:
Initial condition:
solution at t = 29/40
which means currently, the initial boundary will always be 0, which is not ideal (shall not be a big concern though). I am not sure if this is intended. Please let me know if there are some reasons behind this, thanks!
The text was updated successfully, but these errors were encountered:
with periodic boundary condition. In the code, $$a\in[5,10], h_2 \in [0.5,2], c_2 \in [0.7, 0.8]$$.
For example, if $c_2 = 0.8, a = 5, h_2 = 2$, for the second term to be nonzero, we have $x \in [0.4,1.2]$. The problem occurs at the boundary, $x=1$, $u_0(1)$ will be nonzero in this case but $u_0(0)$ is always zero with the current choice of $c_1, w$.
In the current implementation, $u_0(1)$ is not computed as we are using the periodic boundary, but this will lead to a jump of discontinuity in the function definition. The plot I attached in this initial post gives such an example. I am not sure if this is intended.
Hi Professor Lu, thanks for the well-written codes. I am reading the advection data generation code, case 3, where the input function is defined to be a square wave plus a continuous bump, the following are your parameter setting:
Thus, the c2 + a / h2 could be bigger than 1. In pde.solve code, seems like this case is never handled, and because of the periodic boundary condition assumption, the current implementation may have the following inputs:
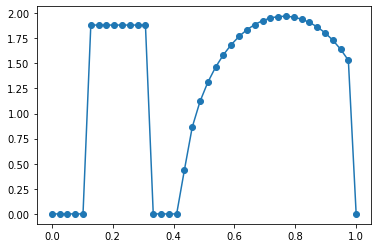
Initial condition:
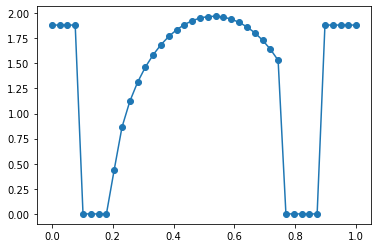
solution at t = 29/40
which means currently, the initial boundary will always be 0, which is not ideal (shall not be a big concern though). I am not sure if this is intended. Please let me know if there are some reasons behind this, thanks!
The text was updated successfully, but these errors were encountered: