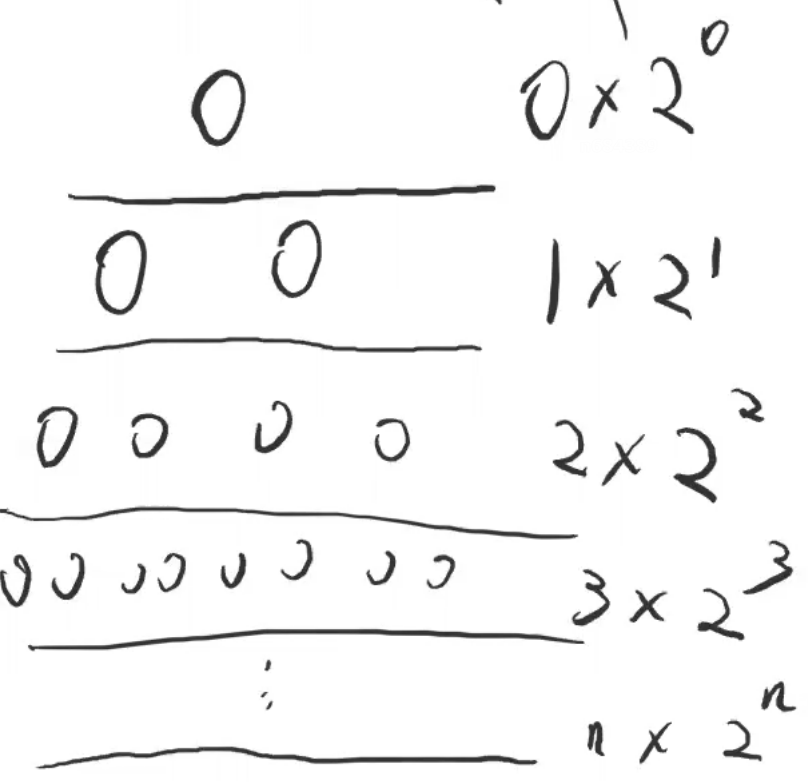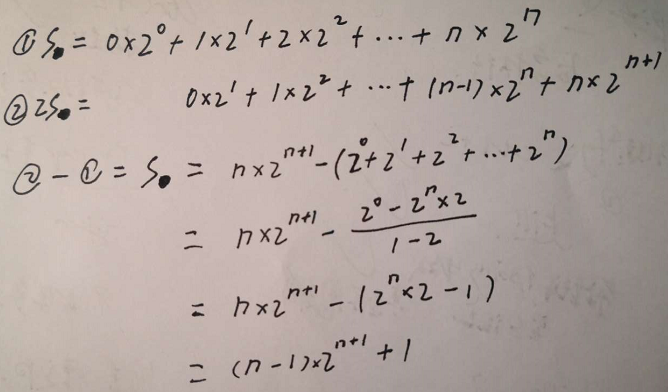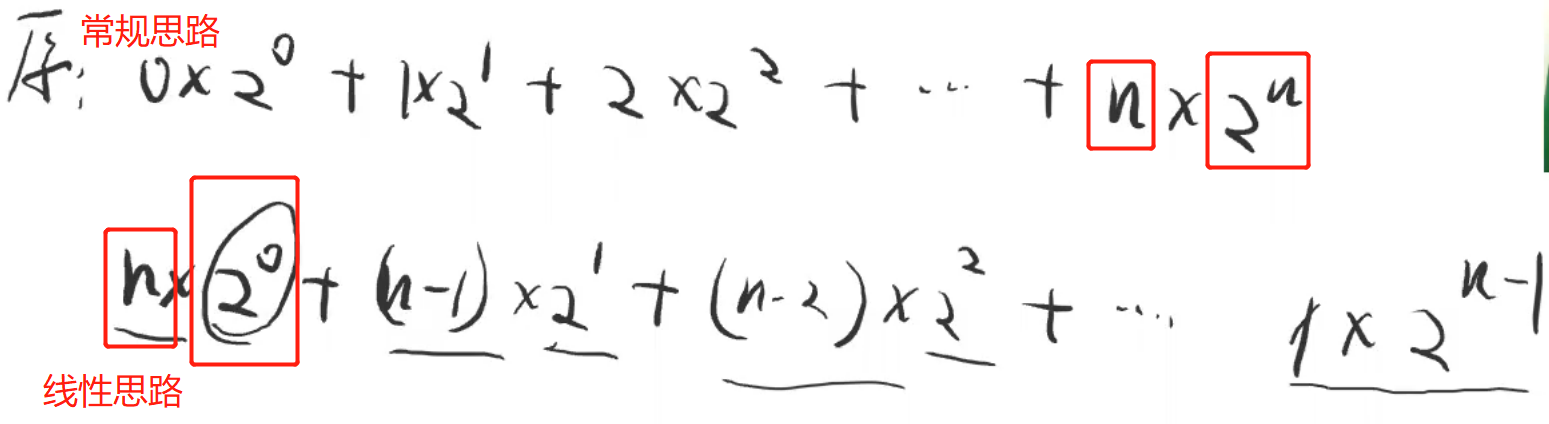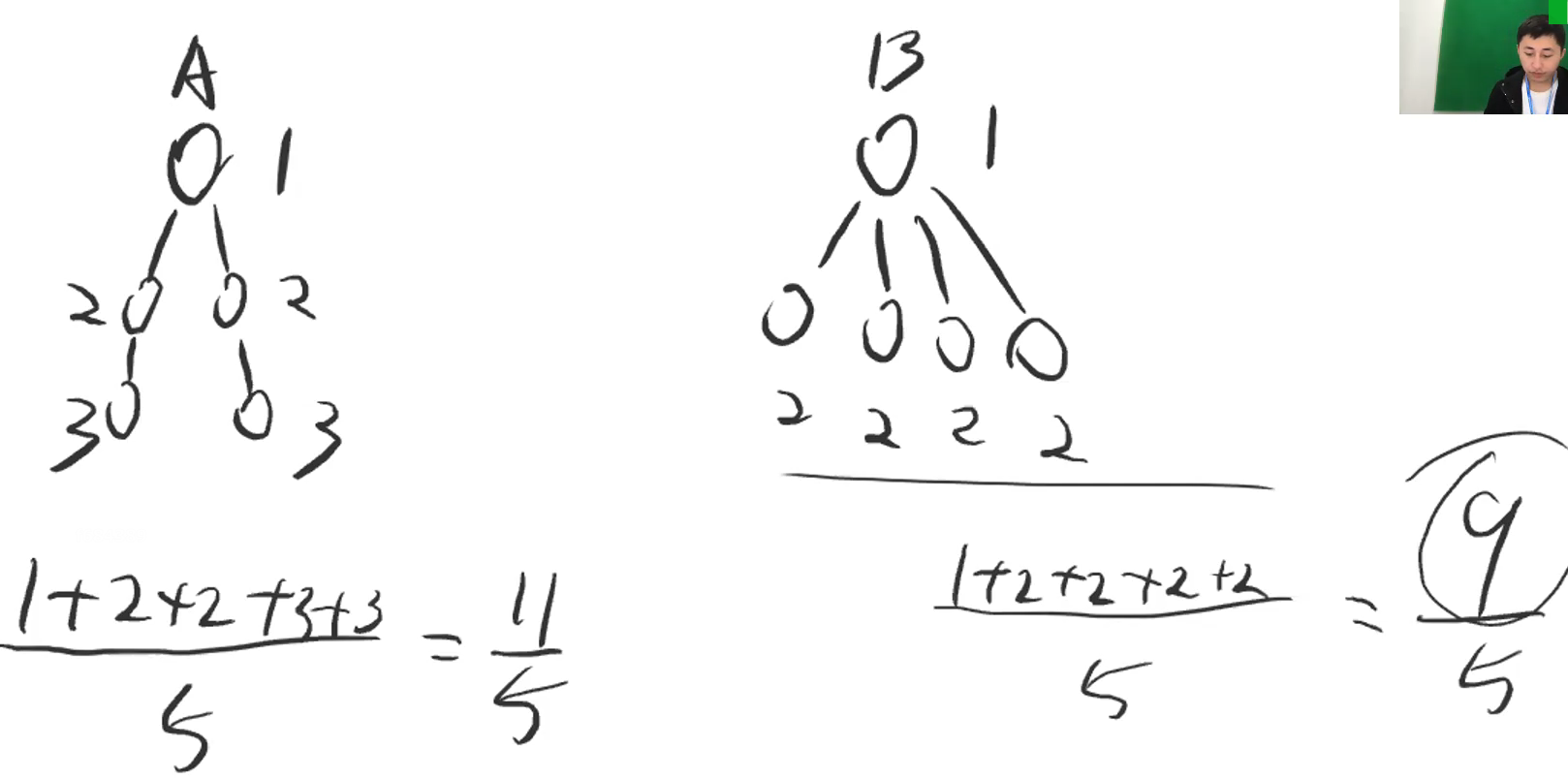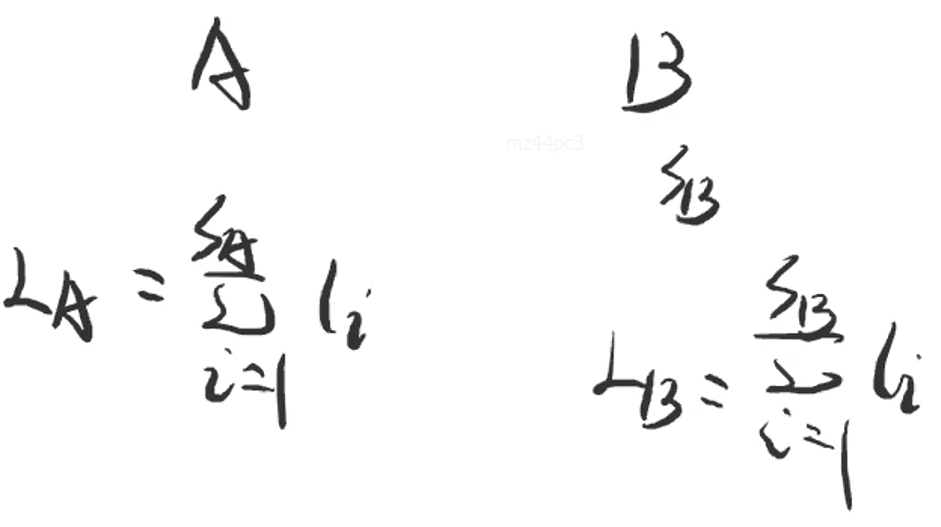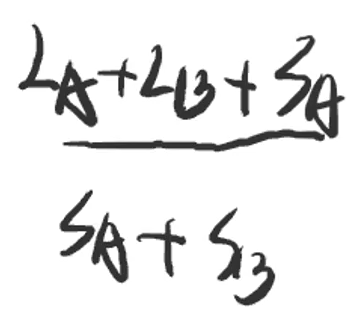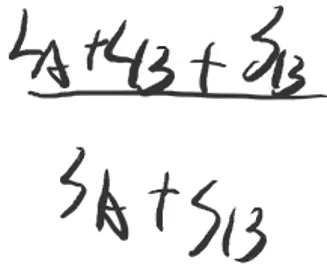程序 = 算法 + 数据结构
程序设计 = 算法 + 数据结构 + 编程范式
算法解决的是计算机的计算资源 而数据结构解决的是计算机的存储资源 解决这两个问题才是一个好的程序 这也就是为什么要学习数据结构的原因
⚡数据结构 = 结构定义 + 结构操作 (对于什么是数据 后面会有更深的理解)
一种功能更为高级的一种数组 它需要开辟一段连续的空间并且空间的每个位置可以存储任意类型
size表示顺序表的大小 length表示当前元素的个数 data_type表示元素的类型
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define COLOR(a, b) "\033[" #b "m" a "\033[0m"
#define GREEN(a) COLOR(a, 32)
typedef struct Vector {
int *data;//指向的是一段自己开辟的类型的空间的首地址
int size, length;
} Vec;
Vec *init(int n) {
Vec *v = (Vec *)malloc(sizeof(Vec));
v->data = (int *)malloc(sizeof(int) * n);
v->size = n;
v->length = 0;
return v;
}
int expand(Vec *v) {
int extr_size = v->size;
//return v->data = (int *)realloc(v->data, sizeof(int) * (v->size + extr_size));
int *p;
while (extr_size) {
//realloc会自动将原来的空间回收掉
p = (int *)realloc(v->data, sizeof(int) * (v->size + extr_size));
//如果p不为空地址 则我们开辟成功 直接break退出循坏 否则一直开辟原来的1/2倍
if (p) break;
extr_size >>= 1;
}
//如果extr_size == 0 则说明真的开不下了 直接返回0值
if (extr_size == 0) return 0;
v->data = p;
v->size += extr_size;
return 1;
}
int insert(Vec *v, int val, int ind) {
if (v == NULL) return 0;
if (ind < 0 || ind > v->length) return 0;
if (v->length == v->size) {
if (!expand(v)) return 0;
printf(GREEN("success to expand! the Vector size is %d\n"), v->size);
}
for (int i = v->length; i > ind; i--) {
v->data[i] = v->data[i - 1];
}
v->data[ind] = val;
v->length += 1;
return 1;
}
int erase(Vec *v, int ind) {
if (v == NULL) return 0;
if (ind < 0 || ind >= v->length) return 0;
for (int i = ind + 1; i < v->length; i++) {
v->data[i - 1] = v->data[i];
}
v->length -= 1;
return 1;
}
//动态开辟空间需要自己手动释放 避免内存泄漏
void clear(Vec *v) {
if (v == NULL) return;
free(v->data);
free(v);
return ;
}
void output(Vec *v) {
if (v == NULL) return;
printf("Vector : [");
for (int i = 0; i < v->length; i++) {
i && printf(", ");
printf("%d", v->data[i]);
}
printf("]\n");
return ;
}
int main() {
srand(time(0));
#define max_op 20
Vec *v = init(2);
for (int i = 0; i < max_op; i++) {
int val = rand() % 100;
int ind = rand() % (v->length + 3) - 1;
int op = rand() % 4;
switch (op) {
case 1:
case 2:
case 0: {
printf("insert %d at %d to Vector = %d\n", val, ind, insert(v, val, ind));
} break;
case 3: {
printf("erase a iterm at %d from Vector = %d\n", ind, erase(v, ind));
} break;
}
output(v);
printf("\n");
}
clear(v);
return 0;
}-
malloc动态内存申请 malloc只是划分一个空间告诉你这个空间是可以用的
- 成功时，返回指向新分配内存开头的指针。
- 为了避免内存泄漏，必须使用free（） 或 realloc（）释放返回的指针。
- 失败时，返回一个空指针。
-
而calloc在开辟空间的时候会将这段空间清0或者是空地址
-
realloc(地址,大小)指的是重新给你分配一段空间
-
第一个参数传进去一个地址 是我们要对哪片空间进行重新划分 而这片空间的首地址就是我们的第一个参数
-
第二个参数是 将现在的这片空间扩大多大的字节数 返回值是新开辟出来的空间的首地址
-
可以在原来的基础上开辟额外的空间 如果还是存不下则会返回NULL值 此时必须格外注意， 不能让原数据域指向它
-
如果开辟了额外空间还是存不下 则会重新分配一段和原空间一样大的空间并且扩大两倍 不过我们在这里让它扩大原来的1/2倍
-
-
链表可以分为两部分
-
程序内部 这里指的就是头指针 我们在程序内部能看到的只有头指针所连接的链表
- 我们可以通过头指针去操作链表
-
内存内部 这部分是链表的本质 在逻辑上如上图一样
- 最后一个节点的指针域为NULL
- 单向链表的指针域又名“后继”；双向链表有“前驱”和“后继”
-
-
对于普通的链表中的指针域 我们称之为后继（当前指针域指向后面节点的地址）
-
-
插入
- ①走到待插入位置的**前一个**位置的节点p - ②先将新的节点x的指针域指向待插入位置的节点p.next - ③将p的指针域指向新的节点x - 顺序不能变！否则可能引发内存泄漏（你想用已经用不了，但系统却以为你在用）-
删除
- 走到待删除节点位置的前一个位置
-
翻转
- 方法一
- 用一个新链表存，使用头插法
- 不断在index = 0 的位置插入节点
- 不足：浪费空间，麻烦
- 方法二
- 原地翻转，用两个变量倒，也是头插法
- 前提：每次操作不要造成内存泄漏
- NULL地址还是在最后面，不会翻转
- 方法一
-
-
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define COLOR(a, b) "\033[" #b "m" a "\033[0m"
#define GREEN(a) COLOR(a, 32)
//链表的结构定义
typedef struct ListNode {
int data;
struct ListNode *next;//struct 结构体类型关键字 虽然我们重命名了ListNode 但是12行还没有生效
} ListNode;
//链表整体的结构定义
typedef struct List {
//ListNode *head;//头指针 因为插入的原则是 在待插入元素前进行插入 当链表为空时 很不好操作
ListNode head;//虚拟头节点 为了方便插入和删除第一个元素
int length;
} List;
//链表的结构操作
//初始化
ListNode *getNewNode(int);
List *getLinkList();
void clear_node(ListNode *);
void clear(List*);
int insert(List *, int, int);
int erase(List *, int);
void output(List *);
void reverse(List *);
int main() {
srand(time(0));
#define max_op 20
List *l = getLinkList();
for (int i = 0; i < max_op; i++) {
int val = rand() % 100;
int ind = rand() % (l->length + 3) - 1;
int op = rand() % 4;
switch (op) {
case 0:
case 1: {
printf("insert %d at %d to List = %d\n", val, ind, insert(l, ind, val));
} break;
case 2: {
printf("erase a iterm at %d from List = %d\n", ind, erase(l, ind));
} break;
case 3: {
printf(GREEN("reverse the list!\n"));
reverse(l);
} break;
}
output(l), printf("\n");
}
#undef max_op
clear(l);
return 0;
}
ListNode *getNewNode(int val) {
ListNode *p = (ListNode *)malloc(sizeof(ListNode));
p->data = val;
p->next = NULL;
return p;
}
List *getLinkList() {
List *l = (List *)malloc(sizeof(List));
l->head.next = NULL;//因为虚拟头节点是一个没有实际意义的节点 所以虚拟头节点指向的后面的那个节点才是真的头节点
l->length = 0;
return l;
}
int insert(List *l, int ind, int val) {
if (l == NULL) return 0;
if (ind < 0 || ind > l->length) return 0;//下标是0 ~ length-1
ListNode *p = &(l->head), *node = getNewNode(val);
while (ind--) p = p->next;
node->next = p->next;
p->next = node;
l->length += 1;
return 1;
}
int erase(List *l, int ind) {
if (l == NULL) return 0;
if (ind < 0 || ind >= l->length) return 0;
ListNode *p = &(l->head), *q;
while (ind--) p = p->next;
q = p->next;
p->next = q->next;
free(q);
l->length -= 1;
return 1;
}
//链表原地翻转 先将头节点指向空 用p 和 q去维护整个链表
void reverse(List *l) {
if (l == NULL) return;
ListNode *p = l->head.next, *q;
l->head.next = NULL;
while (p) {
q = p->next;
p->next = l->head.next;
l->head.next = p;
p = q;
}
return ;
}
void output(List *l) {
if (l == NULL) return ;
printf("List(%d) = [", l->length);
for (ListNode *p = l->head.next; p; p = p->next) {
printf("%d->", p->data);
}
printf("NULL]\n");
return ;
}
void clear_node(ListNode *node) {
if (node == NULL) return;
free(node);
return;
}
void clear(List *l) {
if (l == NULL) return;
ListNode *p = l->head.next, *q;//q中间变量
while (p) {
q = p->next;
clear_node(p);
p = q;
}
free(l);
return ;
}- ⭐初始化数据结构[比如链表、链表结点]时，为什么要动态开辟内存[用malloc等]，而不是定义普通变量？
- 首先，排除盲区：用指针才能接受malloc返回的地址，但指针也能指向普通变量
- 关键：【malloc申请的内存在堆空间，普通变量定义在栈空间(在函数里面定义的)】
- 栈空间：大小只有8MB；出了函数[作用域]变量就被自动释放了
- 堆空间：可分配大内存；变量生命周期长，一般需手动释放
- ❓虚拟头结点定义为普通变量和指针变量的区别
- 个人理解，用指针变量，是为了接收malloc返回的地址
- 而虚拟头结点，在这只是一个指示作用，不需要大空间，所以用普通变量即可而
队列 先进先出的数据结构（First in First out） 从队尾加入（push）一个元素 从队首弹出（pop）一个元素
head记录队首元素的位置 tail记录队尾元素的位置
- 出队： 让head指向下一个元素 长度和容量都不变
- 入队：让tail指向后一个地址 在此地址中进行加入元素
-
假溢出问题：当队列如下图时 弹出了3个元素且加入了4个元素使得队列满了 我们可以发现
tail已经走到了末尾 如果此时我们还想插入一个元素10 该怎么办呢？ 其实之前我们弹出了3个元素 这3个空间是可以使用的 那么我们是否可以将tail指向被弹出的元素的地址（队列的头部）呢？ 答案是可以的 当我们这么做时 此时的队列就变成了==循环队列==
循环队列就是用于解决这种假溢出问题的
那么我们如何去判断一个队列是否是满的呢？ 在循环队列中我们还需要加入一个字段count用于记录有效元素个数
==普通队列==
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
typedef struct Queue {
int *data;
int head, tail, length;//length 容量
} Queue;
Queue *init(int n) {
Queue *q = (Queue *)malloc(sizeof(Queue));
q->data = (int *)malloc(sizeof(int) * n);
q->length = n;
q->head = q->tail = 0;//tail有两种实现方式 1.指向最后一个元素的地址 2.指向最后一个元素的下一个地址 这里我们选择第二种
return q;
}
int front(Queue *q) {
//if (q == NULL) return 0;
return q->data[q->head];
}
int empty(Queue *q) {
return q->head == q->tail; //tail 指向的是最后一个元素的下一个
}
int push(Queue *q, int val) {
if (q == NULL) return 0;
if (q->tail == q->length) return 0;
q->data[q->tail++] = val;//将val放入tail指向的位置 然后将tail++操作
return 1;
}
int pop(Queue *q) {
if (q == NULL) return 0;
if (empty(q)) return 0;//判断当前队列是否为空
q->head++;
return 1;
}
void output(Queue *q) {
if (q == NULL) return;
printf("Queue : [");
for (int i = q->head, j = 0; i < q->tail; i++, j++) {
j && printf(", "); //打印逗号和空格
printf("%d", q->data[i]);
}
printf("]\n");
return ;
}
void clear(Queue *q) {
if (q == NULL) return ;
free(q->data);
free(q);
return;
}
int main() {
srand(time(0));
#define max_op 20
Queue *q = init(max_op);
for (int i = 0; i < max_op; i++) {
int val = rand() % 100;
int op = rand() % 4;
switch (op) {
case 0:
case 1:
case 2: {
printf("push %d to the Queue! ", val);
printf("result = %d\n", push(q, val));
} break;
case 3: {
printf("pop %d from the Queue! ", front(q));
printf("result = %d\n", pop(q));
} break;
}
output(q), printf("\n");
}
#undef max_op
clear(q);
return 0;
}==循环队列==
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define COLOR(a, b) "\033[" #b "m" a "\033[0m"
#define GREEN(a) COLOR(a, 32)
typedef struct Queue {
int *data;//队列数据域
int head, tail, length;//length 容量
int cnt;//循环队列的字段
} Queue;
Queue *init(int n) {
Queue *q = (Queue *)malloc(sizeof(Queue));
q->data = (int *)malloc(sizeof(int) * n);
q->length = n;
q->head = q->tail = 0;//tail有两种实现方式 1.指向最后一个元素的地址 2.指向最后一个元素的下一个地址，方便循环队列判空
q->cnt = 0;
return q;
}
int front(Queue *q) {
//if (q == NULL) return 0;
return q->data[q->head];
}
int empty(Queue *q) {
// return q->head == q->tail; //tail 指向的是最后一个元素的下一个
return q->cnt == 0;//循环队列判空
}
//遇到真溢出
//realloc不适用 尽管它能重新给我们分配一段大的空间 但是进行数据拷贝时是从0地址到尾地址进行拷贝 tail可能在head的前面
int expand(Queue *q) {
int extr_size = q->length;
int *p;
while (extr_size) {
p = (int *)malloc(sizeof(int) * (q->length + extr_size));
if (p) break;
extr_size >>= 1;
}
if (p == NULL) return 0;
for (int i = q->head, j = 0; j < q->cnt; j++) {
p[j] = q->data[(i + j) % q->length];
}
free(q->data);
q->data = p;
q->length += extr_size;
q->head = 0;
q->tail = q->cnt;
return 1;
}
int push(Queue *q, int val) {
if (q == NULL) return 0;
//if (q->tail == q->length) return 0;
if (q->cnt == q->length) {
if (!expand(q)) return 0; //扩容操作
printf(GREEN("expand successfully! Queue->size(%d)\n"), q->length);
}
q->data[q->tail++] = val;//将val放入tail指向的位置 然后将tail++操作
if (q->tail == q->length) q->tail = 0;
q->cnt += 1;
return 1;
}
int pop(Queue *q) {
if (q == NULL) return 0;
if (empty(q)) return 0;//判断当前队列是否为空
q->head++;
if (q->head == q->length) q->head = 0;//head也可能越界
q->cnt -= 1;
return 1;
}
void output(Queue *q) {
if (q == NULL) return;
printf("Queue : [");
for (int i = q->head, j = 0; j < q->cnt; i++, j++) {
j && printf(", "); //打印逗号和空格
printf("%d", q->data[i % q->length]); //取模得到真实的位置
}
printf("]\n");
return ;
}
void clear(Queue *q) {
if (q == NULL) return ;
free(q->data);
free(q);
return;
}
int main() {
srand(time(0));
#define max_op 20
Queue *q = init(2);
for (int i = 0; i < max_op; i++) {
int val = rand() % 100;
int op = rand() % 4;
switch (op) {
case 0:
case 1:
case 2: {
printf("push %d to the Queue! ", val);
printf("result = %d\n", push(q, val));
} break;
case 3: {
printf("pop %d from the Queue! ", front(q));
printf("result = %d\n", pop(q));
} break;
}
output(q), printf("\n");
}
#undef max_op
clear(q);
return 0;
}==栈==
- 一种先进后出的数据结构 （FILO）
- 如果是一个空栈 top = -1 因为顺序结构下标从0~n-1进行访问
-
出栈
-
将栈顶指针向下移动一位
-
出栈要进行判空操作
-
-
入栈
- 将栈顶指针向上移动
- 要进行判断边界操作
struct Stack {
char *val;
int p, maxSize;
};
void initStack(struct Stack *s, int maxSize) {
s->val = malloc(maxSize);
s->p = 0;
}
bool emptyStack(struct Stack *s) {
return !(s->p);
}
void pushStack(struct Stack *s, char c) {
s->val[s->p++] = c;
}
void popStack(struct Stack *s) {
--(s->p);
}
char seekStack(struct Stack *s) {
return s->val[s->p - 1];
}
bool isValid(char * s){
struct Stack stack;
int len = strlen(s);
initStack(&stack, len);
for (int i = 0; i < len; i++) {
switch (s[i]) {
case '(':
case '[':
case '{':
pushStack(&stack, s[i]);
break;
case ')':
if (emptyStack(&stack)) return false;
if (seekStack(&stack) != '(') return false;
popStack(&stack);
break;
case ']':
if (emptyStack(&stack)) return false;
if (seekStack(&stack) != ']') return false;
popStack(&stack);
break;
case '}':
if (emptyStack(&stack)) return false;
if (seekStack(&stack) != '}') return false;
popStack(&stack);
break;
}
}
return emptyStack(&stack);
}==栈的代码==
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define COLOR(a, b) "\033[" #b "m" a "\033[0m"
#define GREEN(a) COLOR(a, 32)
typedef struct Stack {
int *data;
int size, top;//size容量 top栈顶指针
} Stack;
Stack *init(int n) {
Stack *s = (Stack *)malloc(sizeof(Stack));
s->data = (int *)malloc(sizeof(int) * n);
s->size = n;
s->top = -1;
return s;
}
int top(Stack *s) {
return s->data[s->top];
}
int empty(Stack *s) {
return s->top == -1;
}
int expand(Stack *s) {
int extr_size = s->size;
int *p;
while (extr_size) {
p = (int *)realloc(s->data, sizeof(int) * (s->size + extr_size));
if (p) break;
extr_size >>= 1;
}
if (p == NULL) return 0;
s->data = p;
s->size += extr_size;
return 1;
}
int push(Stack *s, int val) {
if (s == NULL) return 0;
if (s->top == s->size - 1) {
if (!expand(s)) return 0;
printf(GREEN("expand successfully! stack->size = (%d)\n"), s->size);
}
s->data[++(s->top)] = val;
return 1;
}
int pop(Stack *s) {
if (s == NULL) return 0;
if (empty(s)) return 0;
s->top -= 1;
return 1;
}
void output(Stack *s) {
if (s == NULL) return ;
printf("[");
for (int i = 0; i <= s->top; i++) {
i && printf(", ");
printf("%d", s->data[i]);
}
printf("]\n");
return ;
}
void clear(Stack *s) {
if (s == NULL ) return;
free(s->data);
free(s);
return ;
}
int main() {
srand(time(0));
#define max_op 20
Stack *s = init(4);
int flag;
for (int i = 0; i < max_op; i++) {
int val = rand() % 100;
int op = rand() % 4;
switch (op) {
case 0:
case 1:
case 2: {
printf("push %d to the Stack = %d\n", val, push(s, val));
} break;
case 3: {
flag = !empty(s);
flag && printf("pop %d frome the Stack", top(s));
printf("result = %d\n", pop(s));
} break;
}
output(s), printf("\n");
}
#undef max_op
clear(s);
return 0;
}
树的组成：结点 + 边
- 结点 👉 集合，边 👉 关系
- 根结点：全集；子结点：子集
- 根结点的所有子结点的集合并集 = 全集
- 【思想】大问题抽象为树，小问题抽象为子结点
- 深度、高度
- 树的深度和高度是一个值：最大层数
- 结点的深度和高度不一样
- 深度：从根结点往下数，该结点是第几层
- 高度：从最深的层数往上数，该结点是第几层
- 度：有几个子孩子
- ⭐【重要公式】结点数 = 边数 + 1
- 二叉树
- 任何树都可以变成一颗二叉树
-
- 这是一颗三叉树 可以把它变成二叉树二进制可以转换成任何进制，二叉树同理
- 首先简单
- 且可以表示所有的树形结构
- 方法：左孩子、右兄弟法，又称十字链表法
- 从上往下，从左往右，结点的孩子放在左边，结点的相邻兄弟放在右边
-
⭐【重要公式】二叉树中，度为0的结点比度为2的结点多1个
-
利用另一重要公式：结点数 = 边数 + 1
-
令ni表示度为i的结点个数
-
则：[结点数] n0 + n1 + n2 = n1 + 2 * n2 + 1 [边数 + 1]
-
得：n0 = n2 + 1
-
完全二叉树：只差最后一个右孩子
-
满二叉树： 只有度为0 和度为2 的节点
-
完美二叉树： 不多不少很完美
- 对于一颗二叉树
- 若根节点表示i
- 左孩子为 2*i
- 右孩子为 2*i + 1
- 若根节点表示i
==binary_tree==
- 实现的是二叉查找树（二叉排序树）
- 维护的性质: 对于一个三元组来说👇
- 左孩子小于根节点
- 右孩子大于根节点
- 对于中序遍历而言 ： 可以实现从小到大排序
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
//节点
typedef struct Node {
int data;
struct Node *lchild, *rchild;//二叉 指针域 左孩子 右孩子
} Node;
typedef struct tree {
Node *root;//指向根节点的指针变量
int n;//节点个数
} Tree;
Node *getNewNode(int val) {
Node *p = (Node *)malloc(sizeof(Node));
p->data = val;
p->lchild = p->rchild = NULL;
return p;
}
Tree *getNewTree() {
Tree *tree = (Tree *)malloc(sizeof(Tree));
tree->root = NULL;
tree->n = 0;
return tree;
}
void clearNode(Node *node) {
if (node == NULL) return ;
clearNode(node->lchild);//沿着当前节点的左子树进行递归回收
clearNode(node->rchild);
free(node);//回收当前节点
return ;
}
void clear(Tree *tree) {
if (tree == NULL) return ;
clearNode(tree->root);
free(tree);
return ;
}
Node *insert_node(Node *root, int val, int *flag) {
if (root == NULL){
*flag = 1;//root为空表示插入成功
return getNewNode(val);//若root节点为空 则将val封装成根节点
}
if (root->data == val) return root;//如果根节点的值等于val 则返回root
//如果当前的val值小于当前根节点所指向的值
//那么我们需要将val值递归插入到根节点的左子树中
if (val < root->data) root->lchild = insert_node(root->lchild, val, flag);
else root->rchild = insert_node(root->rchild, val, flag);
return root;
}
//二叉查找树 左孩子小于根节点 右孩子大于根节点
void insert(Tree *tree, int val) {
int flag = 0;//传出参数
tree->root = insert_node(tree->root, val, &flag);
//若插入成功 则此时flag = 1 且将节点个数加1
tree->n += flag;
return ;
}
void pre_order_node(Node *node) {
if (node == NULL) return ;
printf("%d ", node->data);
pre_order_node(node->lchild);
pre_order_node(node->rchild);
return ;
}
//前序遍历
void pre_order(Tree *tree) {
if (tree == NULL) return ;
printf("pre_order :");
pre_order_node(tree->root);
printf("\n");
return;
}
void in_order_node(Node *node) {
if (node == NULL) return ;
in_order_node(node->lchild);
printf("%d ", node->data);
in_order_node(node->rchild);
return ;
}
//中序遍历
void in_order(Tree *tree) {
if (tree == NULL) return ;
printf("in_order :");
in_order_node(tree->root);
printf("\n");
return;
}
void post_order_node(Node *node) {
if (node == NULL) return ;
post_order_node(node->lchild);
post_order_node(node->rchild);
printf("%d ", node->data);
return ;
}
//后序遍历
void post_order(Tree *tree) {
if (tree == NULL) return ;
printf("post_order :");
post_order_node(tree->root);
printf("\n");
return;
}
//打印广义表
void output_node(Node *root) {
if (root == NULL) return ;
printf("%d", root->data);
if (root->lchild == NULL && root->rchild == NULL) return;
//打印左子树时先输出`(`
printf("(");
output_node(root->lchild);
printf(", ");
//打印右子树后输出`)`
output_node(root->rchild);
printf(")");
return ;
}
void output(Tree *tree) {
if (tree == NULL) return ;
printf("tree(%d) : ", tree->n);
output_node(tree->root);
printf("\n");
return ;
}
int main() {
srand(time(0));
Tree *tree =getNewTree();
#define max_op 10
for (int i = 0; i < max_op; i++) {
int val = rand() % 100;
insert(tree, val);
output(tree);
}
pre_order(tree);
in_order(tree);
post_order(tree);
#undef max_op
clear(tree);
return 0;
}- 😎三种遍历方式中 任选两种（其中必须包含中序遍历）可以还原一颗二叉树
==广义表转二叉树==
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef struct Node {
char data;
struct Node *lchild, *rchild;
} Node;
typedef struct Tree {
Node *root;
int n;
} Tree;
typedef struct Stack {
Node **data;
int top, size;
} Stack;
Node *getNewNode(char val) {
Node *p = (Node *)malloc(sizeof(Node));
p->data = val;
p->lchild = p->rchild = NULL;
return p;
}
Tree *getNewTree() {
Tree *tree = (Tree *)malloc(sizeof(Tree));
tree->root = NULL;
tree->n = 0;
return tree;
}
Stack *init_stack(int n) {
Stack *s = (Stack *)malloc(sizeof(Stack));
s->data = (Node **)malloc(sizeof(Node *) * n);
s->top = -1;
s->size = n;
return s;
}
Node *top(Stack *s) {
return s->data[s->top];
}
int empty(Stack *s) {
return s->top == -1;
}
int push(Stack *s, Node *val) {
if (s == NULL) return 0;
if (s->top == s->size - 1) return 0;
s->data[++(s->top)] = val;
return 1;
}
int pop(Stack *s) {
if (s == NULL) return 0;
if (empty(s)) return 0;
s->top -= 1;
return 1;
}
void clear_stack(Stack *s) {
if (s == NULL) return;
free(s->data);
free(s);
return ;
}
void clear_node(Node *node) {
if (node == NULL) return ;
clear_node(node->lchild);
clear_node(node->rchild);
free(node);
return ;
}
void clear_tree(Tree *tree) {
if (tree == NULL) return ;
clear_node(tree->root);
free(tree);
return ;
}
Node *build(const char *str, int *node_num) {
Stack *s = init_stack(strlen(str));
int flag = 0;
Node *temp = NULL, *p = NULL;
while (str[0]) {
switch (str[0]) {
case '(': {
push(s, temp);
flag = 0;
} break;
case ')': {
p = top(s);
pop(s);
} break;
case ',': {
flag = 1;
} break;
case ' ': break;
default:
temp = getNewNode(str[0]);
if (!empty(s) && flag == 0) {
top(s)->lchild = temp;
} else if (!empty(s) && flag == 1) {
top(s)->rchild = temp;
}
++(*node_num);
break;
}
++str;
}
clear_stack(s);
if (temp && !p) p = temp;
return p;
}
void pre_order_node(Node *root) {
if (root == NULL) return ;
printf("%c ", root->data);
pre_order_node(root->lchild);
pre_order_node(root->rchild);
return ;
}
void pre_order(Tree *tree) {
if (tree == NULL) return ;
printf("pre_order : ");
pre_order_node(tree->root);
printf("\n");
return ;
}
void in_order_node(Node *root) {
if (root == NULL) return ;
in_order_node(root->lchild);
printf("%c ", root->data);
in_order_node(root->rchild);
return ;
}
void in_order(Tree *tree) {
if (tree == NULL) return ;
printf("in_order : ");
in_order_node(tree->root);
printf("\n");
return ;
}
void post_order_node(Node *root) {
if (root == NULL) return ;
post_order_node(root->lchild);
post_order_node(root->rchild);
printf("%c ", root->data);
return ;
}
void post_order(Tree *tree) {
if (tree == NULL) return ;
printf("post_order : ");
post_order_node(tree->root);
printf("\n");
return ;
}
int main() {
char str[1000] = {0};
int node_num = 0;
scanf("%[^\n]s", str);
Tree *tree = getNewTree();
tree->root = build(str, &node_num);
tree->n = node_num;
pre_order(tree);
in_order(tree);
post_order(tree);
clear_tree(tree);
return 0;
}
==稳定排序==
对于相同的元素 经过排序操作后 他们的相对位置保持不变 这样的排序我们称为稳定排序
-
插入排序
- 时间复杂度O(n^2) 至少要n-1轮操作
-
-
冒泡排序
-
归并排序
-
时间复杂度O(nlog·N) 分治思想 不是基于比较跟交换的排序方式
-
==★==这是一个外部排序（很重要）
-
外部排序: 我们可以将数据分为多段加载到内存中
-
内部排序：需要将数据整个加载到内存中进行排序
-
比如我们有40G的数据要进行排序 怎么办？ 我们可以使用归并排序 把40G的数据分成20G 再不行就分成10G
-
#include <stdio.h> #include <stdlib.h> #include <string.h> #include <time.h> #define swap(a, b) {\ a ^= b; b ^= a; a ^= b;\ } #define TEST(arr, n, func, args...) {\ int *num = (int *)malloc(sizeof(int) * n);\ memcpy(num, arr, sizeof(int) * n);\ output(num, n);\ printf("%s= ", #func);\ func(args);\ output(num, n);\ free(num);\ } //插入排序 void insert_sort(int *num, int n) { for (int i = 1; i < n; i++) { for (int j = i ; j > 0 && num[j] < num[j - 1]; j--) { swap(num[j], num[j - 1]); } } return ; } //冒泡 我们在这里设置一个记录交换次数的值 若是一个从小到大的有序数组 times交换次数必定为0 且时间复杂度为O(n) void bubble_sort(int *num, int n) { int times = 1; // 进行交换的次数 for (int i = 1; i < n && times; i++) {//times == 0 结束循环 times = 0; for (int j = 0; j < n - i; j++) { if (num[j] <= num[j + 1]) continue; //减少缩进 swap(num[j], num[j + 1]); times++; } } return ; } //归并排序 分治思想 用递归 void merge_sort(int *num, int l, int r) { //边界条件 只剩两个元素 if (r - l <= 1) { if (r - l == 1 && num[r] < num[l]) { swap(num[r], num[l]); } return; } int mid = (l + r) >> 1; merge_sort(num, l, mid);//从l 到 mid 进行排序 merge_sort(num, mid + 1, r);//从 mid + 1 到 r 进行排序 //合并 int *temp = (int *)malloc(sizeof(int) * (r - l + 1)); //p1 指向的是 int p1 = l, p2 = mid + 1, k = 0; while (p1 <= mid || p2 <= r) { if (p2 > r || (p1 <= mid && num[p1] <= num[p2])) { temp[k++] = num[p1++]; } else { temp[k++] = num[p2++]; } } //将temp拷贝回num里 memcpy(num + l, temp, sizeof(int) * (r -l + 1)); free(temp); return ; } void randint(int *num, int n) { while (n--) num[n] = rand() % 100; return ; } void output(int *num, int n) { printf("["); for (int i = 0; i < n; i++) { printf("%d ", num[i]); } printf("]\n"); } int main() { srand(time(0)); #define max_n 20 int arr[max_n]; randint(arr, max_n); TEST(arr, max_n, insert_sort, num, max_n); TEST(arr, max_n, bubble_sort, num, max_n); TEST(arr, max_n, merge_sort, num, 0, max_n - 1); #undef max_n return 0; }
-
-
选择排序
-
时间复杂度：O(n^2)
-
不稳定排序 比如 5 3 2 5 1 经过排序后 第一个5的位置变到了最后一个 两个5的相对位置发生了改变
-
-
快速排序
- 时间复杂度：O(nlog·N) 选一个基数 让左半边小于这个基数 右半边大于这个基数
- ①选择头部元素作为基数
- ②有头尾两个指针 尾指针找第一个小于基数的值然后放入头部中 头指针找第一个大于基数的值放入刚刚移走的值的位置
- ③最后指针重叠 放入基数
- 时间复杂度：O(nlog·N) 选一个基数 让左半边小于这个基数 右半边大于这个基数
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
//^= 两个值不能异或自己
#define swap(a, b) {\
__typeof(a) __temp = a;\
a = b; b = __temp;\
}
#define TEST(arr, n, func, args...) {\
int *num = (int *)malloc(sizeof(int) * n);\
memcpy(num, arr, sizeof(int) * n);\
output(num, n);\
printf("%s = ", #func);\
func(args);\
output(num, n);\
free(num);\
}
void select_sort(int *num, int n) {
for (int i = 0; i < n - 1; i++) {
int ind = i;
for (int j = i + 1; j < n; j++) {
if (num[ind] > num[j]) ind = j;
}
swap(num[i], num[ind]);
}
return ;
}
void quick_sort(int *num, int l, int r) {
if (l > r) return ;
int x = l, y = r, z = num[x];
while (x < y) {
while (x < y && num[y] > z) y--;
if (x < y) num[x++] = num[y];
while (x < y && num[x] < z) x++;
if (x < y) num[y--] = num[x];
}
num[x] = z;
quick_sort(num, l, x - 1);
quick_sort(num, x + 1, r);
return ;
}
void randint(int *num, int n) {
while (n--) num[n] = rand() % 100;
return ;
}
void output(int *num, int n) {
printf("[");
for (int i = 0; i < n; i++) {
printf("%d ", num[i]);
}
printf("]\n");
return ;
}
int main() {
srand(time(0));
#define max_n 20
int arr[max_n];
randint(arr, max_n);
TEST(arr, max_n, select_sort, num, max_n);
TEST(arr, max_n, quick_sort, num, 0, max_n - 1);
return 0;
}-
快速排序优化
-
二分查找
-
虚拟头尾指针 一堆0的情况
-
特殊情况① 1111111100000000
-
1 表示满足某种性质 0 表示不满足某种性质
-
-
如果我们的数据全是0 0000000000000 最后mid指向第一个0 我们说不清到底是找到了答案还是没找到 所以我们引入了虚拟头指针 去判断它是否等于-1
-
-
-
特殊情况② 00000000011111111111
-
-
三分查找
#include <stdio.h>
#define P(func) {\
printf("%s = %d\n", #func, func);\
}
int binary_search1(int *num, int n, int x) {
int head = 0, tail = n - 1, mid;
while (head <= tail) {
mid = (head + tail) >> 1;
if (num[mid] == x) return mid;
if (num[mid] < x) head = mid + 1;
else tail = mid - 1;
}
return -1;
}
//111111000000
//head 虚拟头指针
int binary_search2(int *num, int n) {
int head = -1, tail = n - 1, mid;
while (head < tail) {
mid = (head + tail + 1) >> 1;
if (num[mid] == 1) head = mid;
else tail = mid - 1;
}
return head;
}
//00000011111111
//tail 虚拟尾指针
int binary_search3(int *num, int n) {
int head = 0, tail = n, mid;
while (head < tail) {
mid = (head + tail) >> 1;
if (num[mid] == 1) tail = mid;
else head = mid + 1;
}
return head == n ? -1 : head;
}
int main() {
int arr1[10] = {1, 3, 5, 7, 9, 11, 13, 17, 19, 21};
int arr2[10] = {1, 1, 1, 1, 0, 0, 0, 0, 0, 0};
int arr3[10] = {0, 0, 0, 0, 0, 0, 1, 1, 1, 1};
P(binary_search1(arr1, 10, 7));
P(binary_search2(arr2, 10));
P(binary_search3(arr3, 10));
return 0;
}- 时间复杂度：趋近与O(1)
- 是一种用来查找的数据结构（下标与值的访问）
-
可以将任意一种类型映射成数组下标的形式进行访问
- 冲突处理方法（无法避免，但是可以减少发生的概率）
- 放入元素 ：当前我要插入16这个值 用16取模与当前的容量 放入到下标为【7】的位置中
-
- 发生冲突： 我要插入7这个值 7%9 = 7 此时我要把7放入到下标为【7】的位置中 但是【7】的位置中已存在值 这时冲突便发生了
-
-
这是就引出了哈希表很重要的结构： 冲突处理方法
- ①开放定值： 当前7的位置有值 那我就去寻找后面的位置 是否有值 如果没有值就将7放入8的位置
- 容易产生数据堆聚问题 ：数据会集中存储在空间中的某一块区域
- ②再哈希法：在我的哈希表中 我设置了不止一种哈希函数 一种不行 我再用下一种
- ③拉链法：在当前位置我不存储一个元素，我们去存储一个链表，将这个值封装一个节点存在链表的后面
- ④建立公共溢出区：这个区域专门用来存储冲突元素的
- ①开放定值： 当前7的位置有值 那我就去寻找后面的位置 是否有值 如果没有值就将7放入8的位置
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef struct Node {
char *str;
struct Node *next;
} Node;
typedef struct HashTable {
Node **data;//哈希表(也是顺序表)里面存储的是一个地址 地址所指向的类型是Node*类型 拉链法
int size;
} HashTable;
Node *init_node(char *str, Node *head) {
Node *p = (Node *)malloc(sizeof(Node));
p->str = strdup(str);
p->next = head; //头插法
return p;
}
HashTable *init_hashtable(int n) {
HashTable *h = (HashTable *)malloc(sizeof(HashTable));
//利用率和哈希函数冲突概率有关 我们把n扩大一倍 使其只有50%利用率
h->size = n << 1;//哈希表的空间利用率不可能达到100% 一般的空间利用率为50%——90% 工业上达到70%才可以使用
h->data = (Node **)calloc(h->size,sizeof(Node *));//数据的每一位都为0值 都是空地址
return h;
}
//哈希函数
int BKDRHash(char *str) {
//seed是一个素数就行
int seed = 31, hash = 0;
for (int i = 0; str[i]; i++) hash = hash * seed + str[i];
//hash有可能超出整型范围 变成一个负数
//这里的0x7fffffff 表示的是符号位为0 其余位为1的数
return hash & 0x7fffffff;
}
int insert(HashTable *h, char *str) {
int hash = BKDRHash(str);
int ind = hash % h->size;
//将字符串插入到下标为ind的这个位置所对应的链表中
h->data[ind] = init_node(str, h->data[ind]);
return 1;
}
int search(HashTable *h, char *str) {
int hash = BKDRHash(str);
int ind = hash % h->size;
//p指向ind这位链表里存的头节点
Node *p = h->data[ind];
//沿着链表的头节点 遍历链表的每一位 strcmp返回值不为0时代表没找到
while (p && strcmp(p->str, str)) p = p->next;
//如果p 不等于NULL 说明是因为strcmp返回值为0退出的循环 也就是说找到了值
return p != NULL;
}
void clear_node(Node *node) {
if (node == NULL) return ;
Node *p = node, *q;
while (p) {
q = p->next;
free(p->str);
free(p);
p = q;
}
return ;
}
void clear_hashtable(HashTable *h) {
if (h == NULL) return ;
for (int i = 0; i < h->size; i++) {
clear_node(h->data[i]);
}
free(h->data);
free(h);
return ;
}
int main() {
int op;
#define max_n 100
char str[max_n + 5] = {0};
HashTable *h = init_hashtable(max_n + 5);
while (~scanf("%d%s", &op, str)) {
switch (op) {
case 0:
printf("insert %s to HashTable\n", str);
insert(h, str);
break;
case 1:
printf("search %s from HashTable result = %d\n", str, search(h, str));
break;
}
}
#undef max_n
clear_hashtable(h);
return 0;
}
- 完全二叉树默认从1开始编号
- 这样可以保证左孩子、右孩子编号简洁
- [否则] 左孩子编号需为2 * i + 1，右孩子编号需为2 * i + 2
==数据结构： 你定义了一种性质，并且能维护这一种性质，那么这种结构就是一个新的数据结构==
- 优先队列是堆的一个别名
- 堆在思维逻辑上就是一颗完全二叉树
- 尾部插入元素(O(logn))
- 一开始以7为根节点 13为左孩子 右孩子为空 这个三元组进行调整
-
头部弹出调整（删除操作）
- 从头部删除元素 并维护堆的性质进行调整
- 我们让最后一个孩子作为头部元素 自上而下进行调整
-
堆排序
- 我们将堆顶元素和堆尾元素置换 每次调整n-1个元素
- 时间复杂度O(nlogn)：因为每次是一层一层遍历
- 大顶堆：从小到大排序 小顶堆：从大到小排序
-
普通队列与堆的比较
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define swap(a, b) {\
__typeof(a) __temp = a;\
a = b; b = __temp;\
}
typedef struct priority_queue {
int *data;
int cnt, size;//个数， 容量
} priority_queue;
priority_queue *init(int n) {
priority_queue *q = (priority_queue *)malloc(sizeof(priority_queue));
//由于优先队列是以数组的形式进行存储 且在逻辑上是一棵二叉树 所以在这里多开一位
//目的：可以方便计算
q->data = (int *)malloc(sizeof(int) * (n + 1));
q->cnt = 0;
q->size = n;
return q;
}
int empty(priority_queue *q) {
return q->cnt == 0;
}
//堆顶弹出元素
int top(priority_queue *q) {
return q->data[1];
}
int push(priority_queue *q, int val) {
if (q == NULL) return 0;
if (q->cnt == q->size) return 0; //判断堆是否满
q->data[++(q->cnt)] = val; //++(q->cnt)是因为我们从1开始存储所以个数要先加1
int ind = q->cnt; //ind记录的是最后插入元素的下标
//由于我们插入一个元素 要进行向上调整 也就是当前节点需要跟父节点进行比较
// ind >> 1 表示我们的父节点 维护大顶堆
while (ind >> 1 && q->data[ind] > q->data[ind >> 1]) {
swap(q->data[ind], q->data[ind >> 1]);
ind >>= 1; //交换后当前节点等于父节点
}
return 1;
}
int pop(priority_queue *q) {
if (q == NULL) return 0;
if (empty(q)) return 0;
//我们将最后一个节点覆盖掉第一个节点 并让个数减1
q->data[1] = q->data[q->cnt--];
int ind = 1; //调整下标
//左孩子的下标没有超过q->cnt的下标的话 说明ind这个节点有左孩子
while ((ind << 1) <= q->cnt) {
//😱(ind << 1 | 1) 骚操作 表示的是ind * 2 + 1
int temp = ind, l = ind << 1, r = ind << 1 | 1;
if (q->data[l] > q->data[temp]) temp = l;
if (r <= q->cnt && q->data[r] > q->data[temp]) temp = r;
if (temp == ind) break;
swap(q->data[ind], q->data[temp]);
ind = temp;
}
return 1;
}
void clear(priority_queue *q) {
if (q == NULL) return ;
free(q->data);
free(q);
return ;
}
int main() {
srand(time(0));
#define max_op 20
priority_queue *q = init(max_op);
for (int i = 0; i < max_op; i++) {
int val = rand() % 100;
push(q, val);
printf("insert %d to the priority_queue!\n", val);
}
for (int i = 0; i < max_op; i++) {
printf("%d ", top(q));
pop(q);
}
printf("\n");
#undef max_op
clear(q);
return 0;
}- 根据其性质，全部弹出，将得到一个排好序的序列
- ⭐思维转变：堆顶元素的弹出操作 ==> 堆顶元素与堆尾元素交换
- 【如此操作】
- 大顶堆的元素全部弹出👉原数组存储了一个从小到大的排序序列
- [至此，从大顶堆，得到一个特殊的小顶堆]
- 时间复杂度：O(NlogN)
- 消耗的时间在于调整操作，每次调整的时间复杂度是O(logN)，共N个元素，需调整N - 1次
- 弹出操作的时间复杂度是O(1)的
- 时间效率一定不会退化
【若要使用堆排序，首先需要维护一个堆，也就是用普通的序列建堆，下面有2种思路】
又叫插入建堆法
- 按照前述尾部插入的调整方法：自下向上
- 从第0层 [默认根结点在第0层] 开始，计算每一层的最多调整次数：
-
- 第 i 层元素的调整次数为 i，第 i 层的结点数为2 ^ i→ 第 i 层的总调整次数为 i * (2 ^ i)
- 最坏的建堆时间复杂度O(NlogN)，计算过程如下：
- 总的调整次数 S = (n - 1) * 2 ^ (n + 1) + 1，过程如下：
-
- 利用裂项相消法
-
- 上面的n对应层数 - 1 [从第0层开始的]，若令总的结点数为N，则n ≈ log[2]N
- ❗【层数n→结点数N的换算】将n ≈ log[2]N代入S，得到S ≈ Nlog[2]N
- 即最坏的时间复杂度为：O(NlogN)
- 总的调整次数 S = (n - 1) * 2 ^ (n + 1) + 1，过程如下：
也就是【线性建堆法】
-
如图所示
- 常规思路：越到下面层，需要的调整次数越多，也就是权重越大
- ❗ 那是否可以思维反转，把大权重放到前面，让下面结点数多的层的权重减小
- 线性思路：可以！从倒数第二层开始排，【自上向下】调整
-
🆒最坏的建堆时间复杂度O(N)
- 同样利用裂项相消法得到总的调整次数 S = 2 ^ (n + 1) - 2 - n
- 把层数n换算到结点数N，得到S ≈ 2N - 2 - log[2]N
- 即最坏的时间复杂度为：O(N)
-
⭐推荐视频
Linear Time BuildHeap
——Youtube
- 比较了常规建堆和线性建堆两种思路，并有直观的动画演示，加深印象
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define swap(a, b) {\
__typeof(a) __temp = a;\
a = b; b = __temp;\
}
void downUpdate(int *arr, int n, int ind) {
while ((ind << 1) <= n) {
int temp = ind, l = ind << 1, r = ind << 1 | 1;
if (arr[l] > arr[temp]) temp = l;
if (r <= n && arr[r] > arr[temp]) temp = r;
if (ind == temp) break;
swap(arr[temp], arr[ind]);
ind = temp;
}
return ;
}
void heap_sort(int *arr, int n) {
arr -= 1;
//我要从倒数第二层的最右边那个节点进行调整
for (int i = n >> 1; i >= 1; i--) {
downUpdate(arr, n, i);
}
for (int i = n; i > 1; i--) {
swap(arr[i], arr[1]);
downUpdate(arr, i - 1, 1);
}
return ;
}
void output(int *arr, int n) {
printf("[");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("]\n");
return ;
}
int main() {
srand(time(0));
#define max_n 20
int *arr = (int *)malloc(sizeof(int) * max_n);
for (int i = 0; i < max_n; i++) {
arr[i] = rand() % 100;
}
output(arr, max_n);
heap_sort(arr, max_n);
output(arr, max_n);
free(arr);
#undef max_n
return 0;
}
并查集能解决的问题： 具有连通性关系的问题
- 确认连通关系：广义上来说 是将两个集合进行合并成具有连通关系的集合
- 可以判断我们两个点在一个集合中是否具有连通关系
==quick-find算法==
- 核心思想：染色
- 一个颜色，对应一个类别
- 初始化：个体独立，都写成自己的索引，属于一个独立的集合里
- ⭐把和自己连通的所有点的颜色改成要染的颜色
-
-
==quick_union算法==
- 找代表元素👉（找大哥） 对于两个点 我们如果想判断连通性 那么我们就去查看他们的大哥是不是同一个
- 对于集合和集合之间建立的连通关系可以认为是集合和集合之间的合并操作
- 👉 （逻辑上）两颗子树的合并操作
- 👉 最终会在一个根结点下面 也就只有一个代表元素
-
首先链表是一棵极端的树
-
当我们用这种算法时两棵子树可能退化成链表 且有n个节点 则此时的树高也为n
- 合并操作将退化为O(n) →O(树高)
- 联通操作将退化为O(n) →O(树高)
==Weighted quick_union算法==
-
按秩优化
-
如何避免退化？→保证枝繁叶茂
- 合并依据1：树高，矮树挂在高树下[两两结合]
- 高度为 h 的树，至少需要的结点个数N为2 ^ (h - 1)
- 即树高h = log[2]N + 1 ≈ log[2]N
- [PS] 只有两棵一样树高的树合并，才会使高度增加
- 合并依据2：结点数量，结点少的树挂在结点多的树下
- 两种优化方式都能得到O(logN)，但是合并依据2【结点数量】更优秀一些
- 合并依据1：树高，矮树挂在高树下[两两结合]
-
⭐为什么合并依据2更优秀
- 【示例】什么是平均查找次数
- 如下图所示，计算了A、B树的平均查找次数
-
- 结点深度即为结点的查找次数，平均查找次数 = 总查找次数 / 总结点数
- 此示例，B树的查找操作更快
- 【推导】合并依据2直接决定平均查找次数
- 对于有SA、SB个结点的A、B树，它们的总查找次数LA、LB分别为：
-
- 其中，li 代表第 i 个结点的深度
-
- 此时进行合并操作，分别计算①A→B和②B→A的平均查找次数
- ①当A树作为子树合并到B树时，为
-
- A树中的所有结点需要多查找一次
-
- ②当B树作为子树合并到A树时，为
-
- B树中的所有结点需要多查找一次
-
- ①当A树作为子树合并到B树时，为
- ❗【比较两种方式的平均查找次数】
- 和树高[LA、LB]没有直接关系，而分子的结点数量[SA、SB]【直接】决定查找次数，次数越小越好
- 👉谁的结点数少，就作为子树被合并
- ❓思考：上面的推导是否证明高度无法作为合并依据呢？
- ❌否，高度间接影响着结点数量，一般情况高度越低，结点数量越少
- 但是，对于特殊情况，A树比B树高，而A树结点数量却比B树少时，还是按照【结点数量】作为合并依据，将A树作为子树合并到B树里
- 对于有SA、SB个结点的A、B树，它们的总查找次数LA、LB分别为：
- 所以以结点数作为合并依据更优秀！👇合并思路如下
- 【示例】什么是平均查找次数
-
在合并两棵子树时
- 如果结点数一样，就按照普通Quick-Union的思路换
- 如果不一样，结点数少的子树的根结点接在👉结点数多的子树的根结点下面
-
[PS]换句话说
- 在换大哥时
- 如果小弟数量一样，就按照普通Quick-Union的思路换
- 如果不一样，小弟少的大哥得跟👉小弟多的大哥混
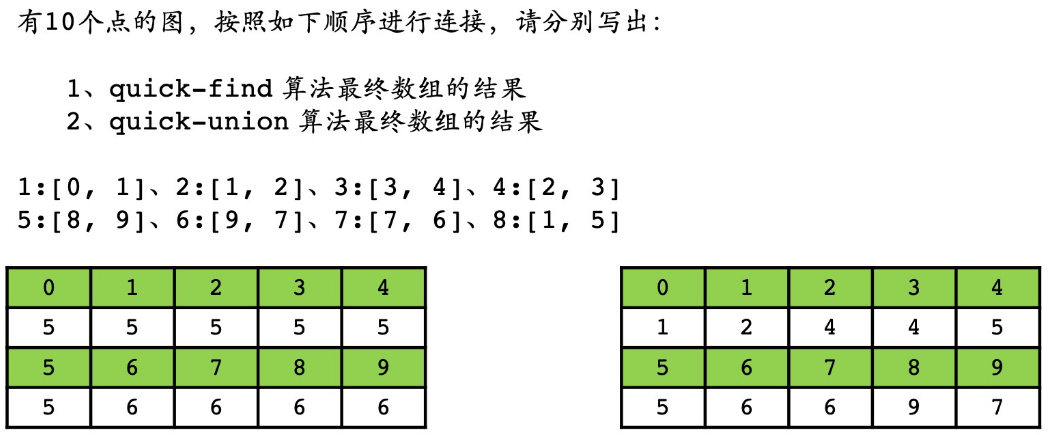
- ==Quick-Find vs. Quick-Union==
-
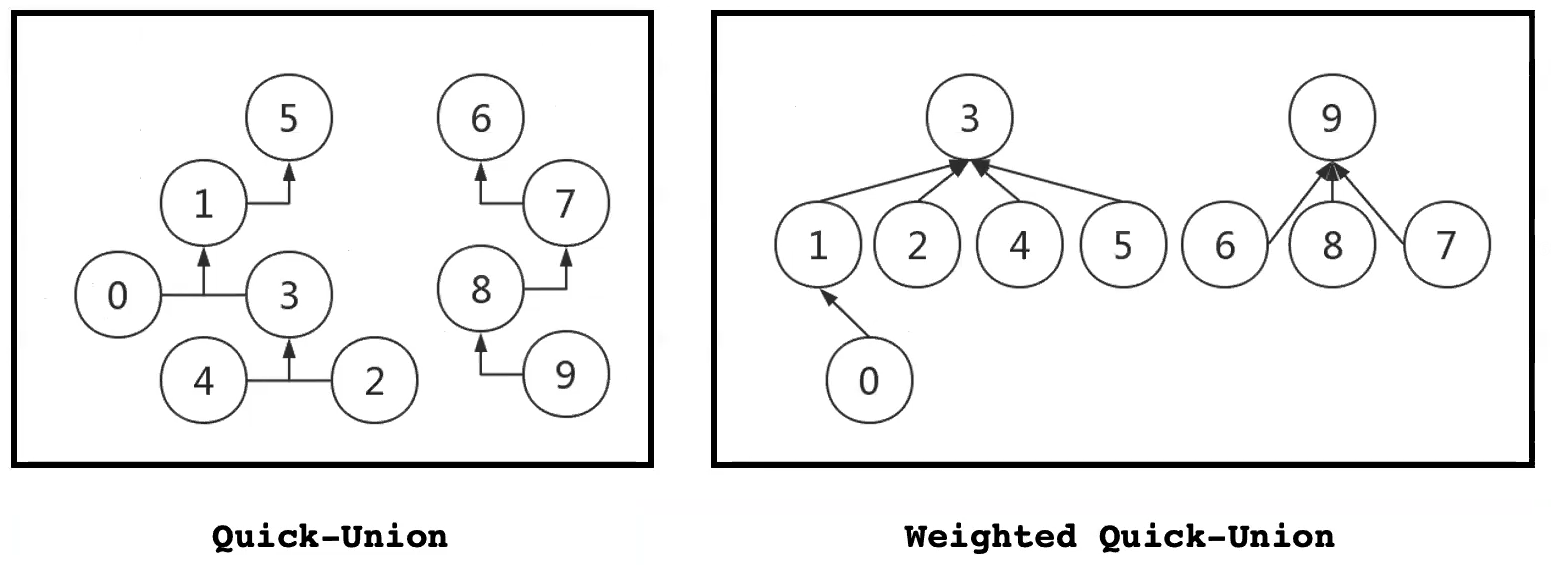
【关键】理解Quick-Union
- 0->1->2->4->5、3->4->5；8->9->7->6
- 查找、合并边界：自己的代表元素就是本身时，停止
-
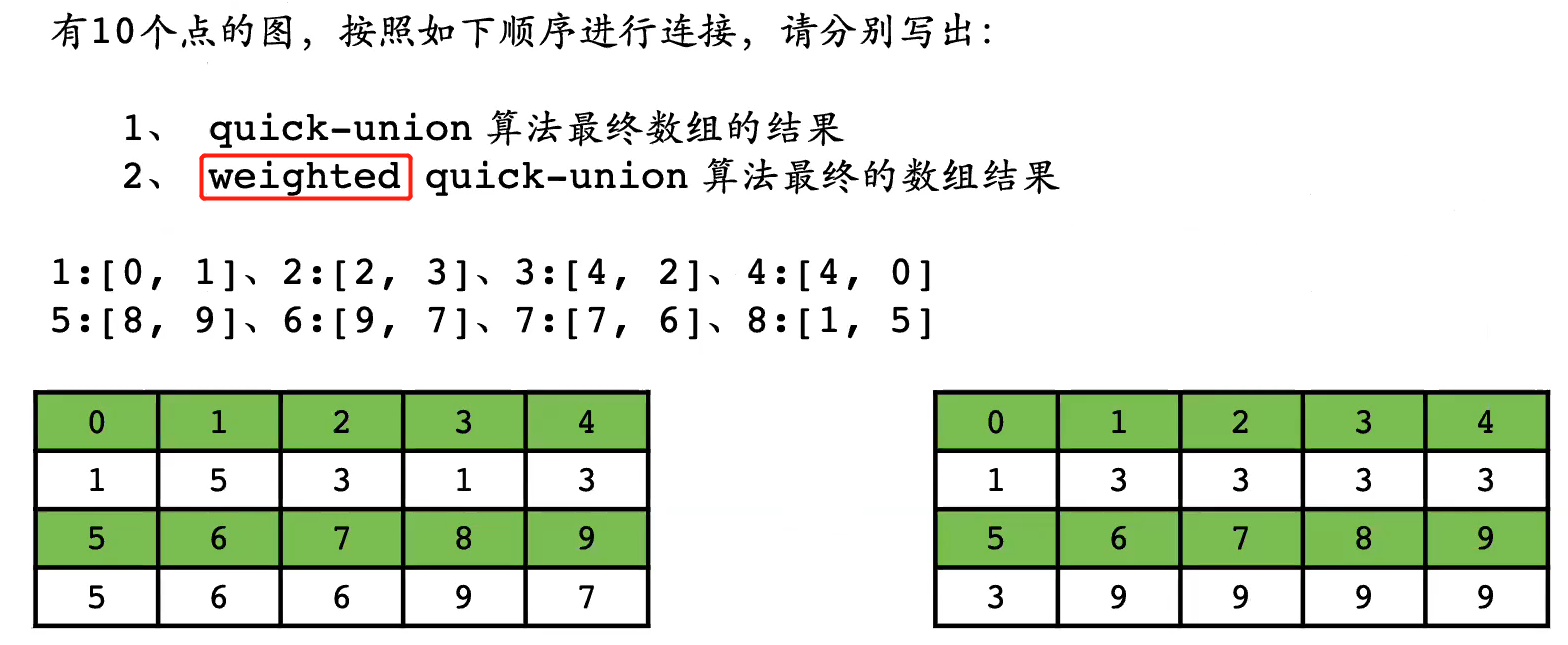
==Quick-Union vs. weighted Quick-Union==
-
【关键】理解weighted的含义
- 当两个集合的元素个数不一样时
- 元素少的集合的代表元素的值👉元素多的集合的代表元素的值
- 小弟少的大哥得跟着小弟多的大哥混
-
结果可视化
-
- 很明显，weighted方法得到的树更矮，合并、查找效率更高
-
-
从练习题入手并查集
样例输入
6 5
1 1 2
2 1 3
1 2 4
1 4 3
2 1 3
样例输出
No
Yes
quick_find
#include <stdio.h>
#include <stdlib.h>
typedef struct UnionSet {
int *color; //需要一片连续的空间存储每个元素的颜色
int n; //color指向这片连续空间的首地址
} UnionSet;
UnionSet *init(int n) {
UnionSet *u = (UnionSet *)malloc(sizeof(UnionSet));
u->color = (int *)malloc(sizeof(int) * (n + 1));
u->n = n;
for (int i = 1; i <= n; i++) {
u->color[i] = i; // 将每个元素初始化为自己
}
return u;
}
int find(UnionSet *u, int x) {
return u->color[x];
}
//合并
int merge(UnionSet *u, int a, int b) {
if (find(u, a) == find(u, b)) return 0; //判断a和b是否连通
int color_a = u->color[a]; //保存前一个变量的颜色
//把所有a的颜色 改为 b的颜色
for (int i = 1; i <= u->n; i++) {
if (u->color[i] - color_a) continue; //若当前i的颜色等与a的颜色 则执行下次循环 否则
u->color[i] = u->color[b]; //将i的颜色改为b的颜色
}
return 1;
}
void clear(UnionSet *u) {
if (u == NULL) return ;
free(u->color);
free(u);
return ;
}
int main() {
int n, m;
scanf("%d%d", &n, &m);
UnionSet *u = init(n);
for (int i = 0; i < m; i++) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
switch (a) {
case 1: merge(u, b, c); break;
case 2: printf("%s\n", find(u, b) == find(u, c) ? "Yes" : "No");
break;
}
}
clear(u);
return 0;
}==Weighted quick_union + 路径压缩==
#include <stdio.h>
#include <stdlib.h>
#define swap(a, b) {\
__typeof(a) __temp = a;\
a = b; b = __temp;\
}
typedef struct UnionSet {
int *father;
int *size; //记录相关的节点个数 weighted quick-union 优化
int n;
} UnionSet;
UnionSet *init(int n) {
UnionSet *u = (UnionSet *)malloc(sizeof(UnionSet));
u->father = (int *)malloc(sizeof(int) * (n + 1));
u->size = (int *)malloc(sizeof(int) * (n + 1));
u->n = n;
for (int i = 1; i <= n; i++) {
u->father[i] = i;
u->size[i] = 1; //最开始相关的节点数为自己 = 1
}
return u;
}
int find(UnionSet *u, int x) {
//if (u->father[x] == x) return x;//返回的是当前元素的代表元素
//return find(u, u->father[x]); //否则我们就递归去找它父亲的父亲
//优化 ：路径压缩 找到最直接的父亲 在路径压缩面前 可以去掉按节点合并的优化操作 其效率差不多
return u->father[x] = (u->father[x] == x ? x : find(u, u->father[x]));
}
int merge(UnionSet *u, int a, int b) {
int fa = find(u, a), fb = find(u, b);
if (fa == fb) return 0;
if (u->size[fa] < u->size[fb]) swap(fa, fb); //当fa的节点个数小于fb的节点个数 交换它们 保证fa的节点数是最大的
u->father[fb] = fa; //把fa当做合并后的根节点
u->size[fa] += u->size[fb]; //当fb作为子树时 fa整体的节点个数要加上fb的
return 1;
}
void clear(UnionSet *u) {
if (u == NULL) return ;
free(u->father);
free(u->size);
free(u);
return ;
}
int main() {
int n, m;
scanf("%d%d", &n, &m);
UnionSet *u = init(n);
for (int i = 0; i < m; i++) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
switch (a) {
case 1: merge(u, b, c); break;
case 2: printf("%s\n", find(u, b) == find(u, c) ? "Yes" : "No");
break;
}
}
clear(u);
return 0;
}