Skip to content

Latest commit

 

History

History
391 lines (327 loc) · 11 KB

README.md

File metadata and controls

391 lines (327 loc) · 11 KB
Raw

2158. 每天绘制新区域的数量

English Version

题目描述

有一幅细长的画，可以用数轴来表示。 给你一个长度为 n 、下标从 0 开始的二维整数数组 paint ，其中 paint[i] = [starti, endi] 表示在第 i 天你需要绘制 starti 和 endi 之间的区域。

多次绘制同一区域会导致不均匀，因此每个区域最多只能绘制 一次 。

返回一个长度为 n 的整数数组 worklog，其中 worklog[i] 是你在第 i 天绘制的 新 区域的数量。

 

示例 1：

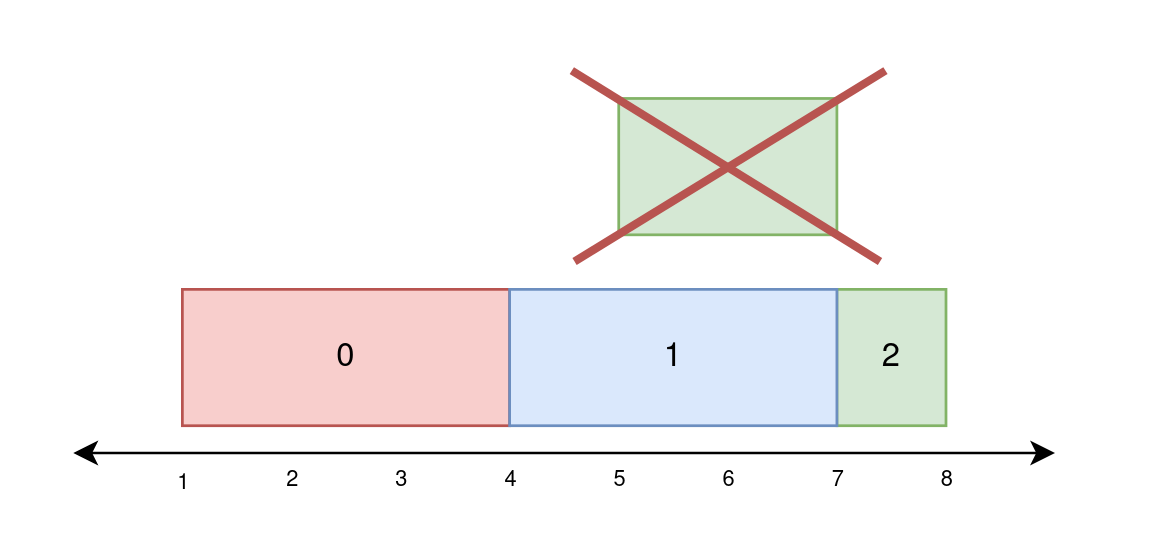
输入：paint = [[1,4],[4,7],[5,8]]
输出：[3,3,1]
解释：
在第 0 天，绘制 1 到 4 之间的所有内容。
第 0 天绘制的新区域数量为 4 - 1 = 3 。
在第 1 天，绘制 4 到 7 之间的所有内容。
第 1 天绘制的新区域数量为 7 - 4 = 3 。
在第 2 天，绘制 7 到 8 之间的所有内容。
5 到 7 之间的所有内容都已在第 1 天绘制完毕。
第 2 天绘制的新区域数量为 8 - 7 = 1 。

示例 2：

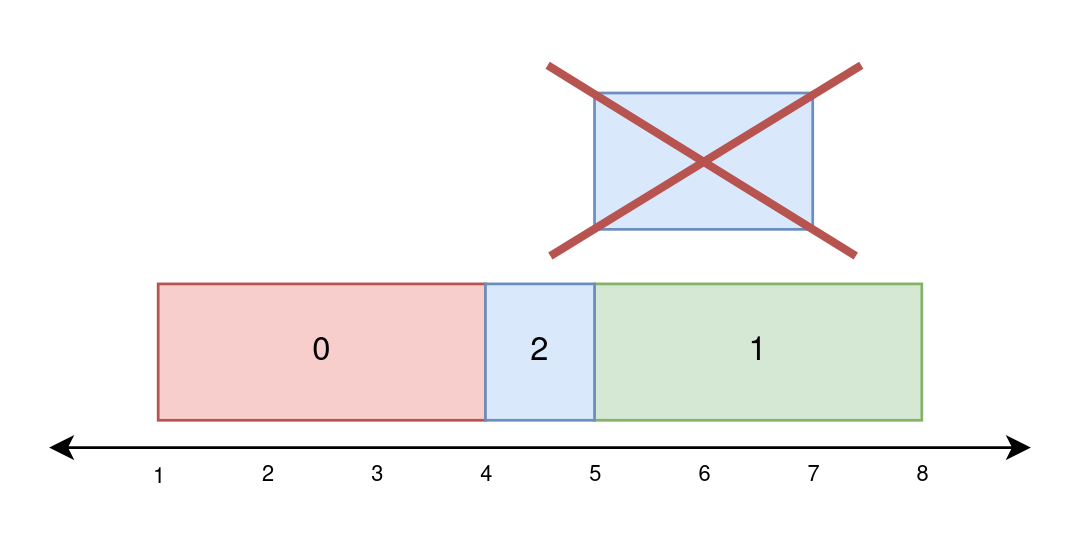
输入：paint = [[1,4],[5,8],[4,7]]
输出：[3,3,1]
解释：
在第 0 天，绘制 1 到 4 之间的所有内容。
第 0 天绘制的新区域数量为 4 - 1 = 3 。
第 1 天，绘制 5 到 8 之间的所有内容。
第 1 天绘制的新区域数量为 8 - 5 = 3 。
在第 2 天，绘制 4 到 5 之间的所有内容。
5 到 7 之间的所有内容都已在第 1 天绘制完毕。
第 2 天绘制的新区域数量为 5 - 4 = 1 。

示例 3：

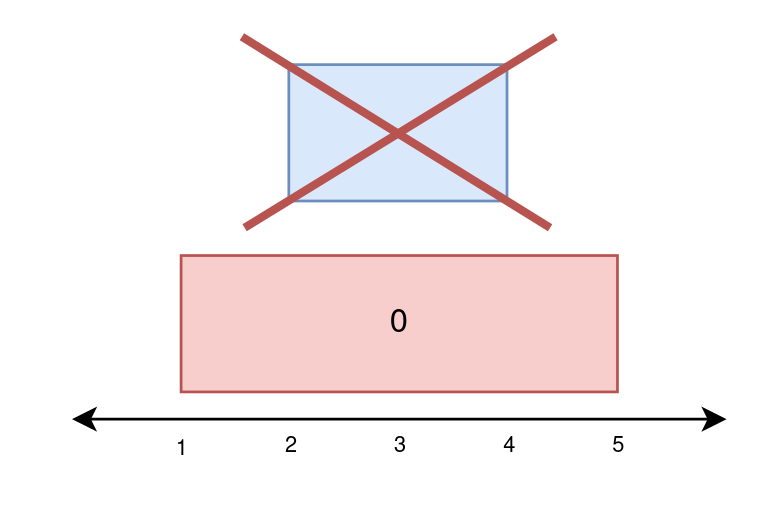
输入：paint = [[1,5],[2,4]]
输出：[4,0]
解释：
在第 0 天，绘制 1 到 5 之间的所有内容。
第 0 天绘制的新区域数量为 5 - 1 = 4 。
在第 1 天，什么都不画，因为第 0 天已经画了 2 到 4 之间的所有内容。
第 1 天绘制的新区域数量为 0 。

 

提示：

  • 1 <= paint.length <= 105
  • paint[i].length == 2
  • 0 <= starti < endi <= 5 * 104

解法

方法一：线段树

线段树将整个区间分割为多个不连续的子区间，子区间的数量不超过 log(width)。更新某个元素的值，只需要更新 log(width) 个区间，并且这些区间都包含在一个包含该元素的大区间内。区间修改时，需要使用懒标记保证效率。

  • 线段树的每个节点代表一个区间；
  • 线段树具有唯一的根节点，代表的区间是整个统计范围，如 [1, N]；
  • 线段树的每个叶子节点代表一个长度为 1 的元区间 [x, x]；
  • 对于每个内部节点 [l, r]，它的左儿子是 [l, mid]，右儿子是 [mid + 1, r], 其中 mid = ⌊(l + r) / 2⌋ (即向下取整)。

对于本题，线段树节点维护的信息有：

  1. 区间中元素大于 0 的个数 v
  2. 懒标记 add

Python3

class Node:
    def __init__(self, l, r):
        self.left = None
        self.right = None
        self.l = l
        self.r = r
        self.mid = (l + r) >> 1
        self.v = 0
        self.add = 0


class SegmentTree:
    def __init__(self):
        self.root = Node(1, 10**5 + 10)

    def modify(self, l, r, v, node=None):
        if l > r:
            return
        if node is None:
            node = self.root
        if node.l >= l and node.r <= r:
            node.v = node.r - node.l + 1
            node.add = v
            return
        self.pushdown(node)
        if l <= node.mid:
            self.modify(l, r, v, node.left)
        if r > node.mid:
            self.modify(l, r, v, node.right)
        self.pushup(node)

    def query(self, l, r, node=None):
        if l > r:
            return 0
        if node is None:
            node = self.root
        if node.l >= l and node.r <= r:
            return node.v
        self.pushdown(node)
        v = 0
        if l <= node.mid:
            v += self.query(l, r, node.left)
        if r > node.mid:
            v += self.query(l, r, node.right)
        return v

    def pushup(self, node):
        node.v = node.left.v + node.right.v

    def pushdown(self, node):
        if node.left is None:
            node.left = Node(node.l, node.mid)
        if node.right is None:
            node.right = Node(node.mid + 1, node.r)
        if node.add:
            left, right = node.left, node.right
            left.v = left.r - left.l + 1
            right.v = right.r - right.l + 1
            left.add = node.add
            right.add = node.add
            node.add = 0


class Solution:
    def amountPainted(self, paint: List[List[int]]) -> List[int]:
        tree = SegmentTree()
        ans = []
        for i, (start, end) in enumerate(paint):
            l, r = start + 1, end
            v = tree.query(l, r)
            ans.append(r - l + 1 - v)
            tree.modify(l, r, 1)
        return ans

Java

class Node {
    Node left;
    Node right;
    int l;
    int r;
    int mid;
    int v;
    int add;

    public Node(int l, int r) {
        this.l = l;
        this.r = r;
        this.mid = (l + r) >> 1;
    }
}

class SegmentTree {
    private Node root = new Node(1, 100010);

    public SegmentTree() {
    }

    public void modify(int l, int r, int v) {
        modify(l, r, v, root);
    }

    public void modify(int l, int r, int v, Node node) {
        if (l > r) {
            return;
        }
        if (node.l >= l && node.r <= r) {
            node.v = node.r - node.l + 1;
            node.add = v;
            return;
        }
        pushdown(node);
        if (l <= node.mid) {
            modify(l, r, v, node.left);
        }
        if (r > node.mid) {
            modify(l, r, v, node.right);
        }
        pushup(node);
    }

    public int query(int l, int r) {
        return query(l, r, root);
    }

    public int query(int l, int r, Node node) {
        if (l > r) {
            return 0;
        }
        if (node.l >= l && node.r <= r) {
            return node.v;
        }
        pushdown(node);
        int v = 0;
        if (l <= node.mid) {
            v += query(l, r, node.left);
        }
        if (r > node.mid) {
            v += query(l, r, node.right);
        }
        return v;
    }

    public void pushup(Node node) {
        node.v = node.left.v + node.right.v;
    }

    public void pushdown(Node node) {
        if (node.left == null) {
            node.left = new Node(node.l, node.mid);
        }
        if (node.right == null) {
            node.right = new Node(node.mid + 1, node.r);
        }
        if (node.add != 0) {
            Node left = node.left, right = node.right;
            left.add = node.add;
            right.add = node.add;
            left.v = left.r - left.l + 1;
            right.v = right.r - right.l + 1;
            node.add = 0;
        }
    }
}

class Solution {
    public int[] amountPainted(int[][] paint) {
        SegmentTree tree = new SegmentTree();
        int n = paint.length;
        int[] ans = new int[n];
        for (int i = 0; i < n; ++i) {
            int l = paint[i][0] + 1;
            int r = paint[i][1];
            int v = tree.query(l, r);
            ans[i] = r - l + 1 - v;
            tree.modify(l, r, 1);
        }
        return ans;
    }
}

C++

class Node {
public:
    Node* left;
    Node* right;
    int l;
    int r;
    int mid;
    int v;
    int add;

    Node(int l, int r) {
        this->l = l;
        this->r = r;
        this->mid = (l + r) >> 1;
        this->left = this->right = nullptr;
        v = add = 0;
    }
};

class SegmentTree {
private:
    Node* root;

public:
    SegmentTree() {
        root = new Node(1, 100010);
    }

    void modify(int l, int r, int v) {
        modify(l, r, v, root);
    }

    void modify(int l, int r, int v, Node* node) {
        if (l > r) return;
        if (node->l >= l && node->r <= r) {
            node->v = node->r - node->l + 1;
            node->add = v;
            return;
        }
        pushdown(node);
        if (l <= node->mid) modify(l, r, v, node->left);
        if (r > node->mid) modify(l, r, v, node->right);
        pushup(node);
    }

    int query(int l, int r) {
        return query(l, r, root);
    }

    int query(int l, int r, Node* node) {
        if (l > r) return 0;
        if (node->l >= l && node->r <= r) return node->v;
        pushdown(node);
        int v = 0;
        if (l <= node->mid) v += query(l, r, node->left);
        if (r > node->mid) v += query(l, r, node->right);
        return v;
    }

    void pushup(Node* node) {
        node->v = node->left->v + node->right->v;
    }

    void pushdown(Node* node) {
        if (!node->left) node->left = new Node(node->l, node->mid);
        if (!node->right) node->right = new Node(node->mid + 1, node->r);
        if (node->add) {
            Node* left = node->left;
            Node* right = node->right;
            left->v = left->r - left->l + 1;
            right->v = right->r - right->l + 1;
            left->add = node->add;
            right->add = node->add;
            node->add = 0;
        }
    }
};

class Solution {
public:
    vector<int> amountPainted(vector<vector<int>>& paint) {
        int n = paint.size();
        vector<int> ans(n);
        SegmentTree* tree = new SegmentTree();
        for (int i = 0; i < n; ++i) {
            int l = paint[i][0] + 1;
            int r = paint[i][1];
            int v = tree->query(l, r);
            ans[i] = r - l + 1 - v;
            tree->modify(l, r, 1);
        }
        return ans;
    }
};

TypeScript



...