You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
{{ message }}
This repository has been archived by the owner on Jul 23, 2019. It is now read-only.
For a given vector , we need a method for calculating the covariant derivative given by:
The covariant derivative should be implemented as an operator, however, the contraction of the input vector with the Christoffel symbols implies that the covariant derivative is not compatible with the current API for tensors.
I propose to simply model the covariant derivative as a tensor operator similar to the DiffOperator in partial.py where it is a subclass of ~sympy.tensor.tensor.TensExpr and defines the __mul__ and __rmul__ magic methods to return an expression of the form provided by the equation above.
The text was updated successfully, but these errors were encountered:
Sign up for freeto subscribe to this conversation on GitHub.
Already have an account?
Sign in.
For a given vector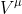 , we need a method for calculating the covariant derivative given by:
, we need a method for calculating the covariant derivative given by:
The covariant derivative should be implemented as an operator, however, the contraction of the input vector with the Christoffel symbols implies that the covariant derivative is not compatible with the current API for tensors.
I propose to simply model the covariant derivative as a tensor operator similar to the DiffOperator in
partial.pywhere it is a subclass of~sympy.tensor.tensor.TensExprand defines the__mul__and__rmul__magic methods to return an expression of the form provided by the equation above.The text was updated successfully, but these errors were encountered: