Skip to content

Latest commit

 

History

History
245 lines (194 loc) · 6.5 KB

README.md

File metadata and controls

245 lines (194 loc) · 6.5 KB
Raw
comments difficulty edit_url tags
true
困难
数组
数学
矩阵
排序

296. 最佳的碰头地点 🔒

English Version

题目描述

给你一个 m x n  的二进制网格 grid ，其中 1 表示某个朋友的家所处的位置。返回 最小的 总行走距离 。

总行走距离 是朋友们家到碰头地点的距离之和。

我们将使用 曼哈顿距离 来计算，其中 distance(p1, p2) = |p2.x - p1.x| + |p2.y - p1.y| 。

 

示例 1：

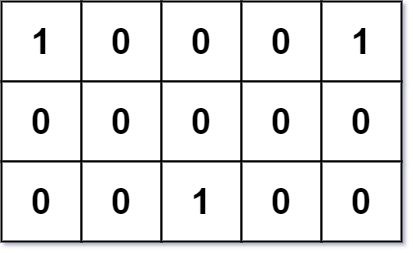
输入: grid = [[1,0,0,0,1],[0,0,0,0,0],[0,0,1,0,0]]
输出: 6 
解释: 给定的三个人分别住在(0,0)，(0,4) 和 (2,2):
     (0,2) 是一个最佳的碰面点，其总行走距离为 2 + 2 + 2 = 6，最小，因此返回 6。

示例 2:

输入: grid = [[1,1]]
输出: 1

 

提示:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 200
  • grid[i][j] == 0 or 1.
  • grid 中 至少 有两个朋友

解法

方法一：排序 + 中位数

对于每一行，我们可以将所有的 $1$ 的下标排序，然后取中位数 $i$ 作为碰头地点的横坐标。

对于每一列，我们可以将所有的 $1$ 的下标排序，然后取中位数 $i$ 作为碰头地点的纵坐标。

最后，我们计算所有 $1$ 到碰头地点 $(i, j)$ 的曼哈顿距离之和即可。

时间复杂度 $O(m\times n\times \log(m\times n))$。最多有 $m\times n$ 个 $1$，排序的时间复杂度为 $\log(m\times n)$。

相似题目：

Python3

class Solution:
    def minTotalDistance(self, grid: List[List[int]]) -> int:
        def f(arr, x):
            return sum(abs(v - x) for v in arr)

        rows, cols = [], []
        for i, row in enumerate(grid):
            for j, v in enumerate(row):
                if v:
                    rows.append(i)
                    cols.append(j)
        cols.sort()
        i = rows[len(rows) >> 1]
        j = cols[len(cols) >> 1]
        return f(rows, i) + f(cols, j)

Java

class Solution {
    public int minTotalDistance(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        List<Integer> rows = new ArrayList<>();
        List<Integer> cols = new ArrayList<>();
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1) {
                    rows.add(i);
                    cols.add(j);
                }
            }
        }
        Collections.sort(cols);
        int i = rows.get(rows.size() >> 1);
        int j = cols.get(cols.size() >> 1);
        return f(rows, i) + f(cols, j);
    }

    private int f(List<Integer> arr, int x) {
        int s = 0;
        for (int v : arr) {
            s += Math.abs(v - x);
        }
        return s;
    }
}

C++

class Solution {
public:
    int minTotalDistance(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        vector<int> rows;
        vector<int> cols;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j]) {
                    rows.emplace_back(i);
                    cols.emplace_back(j);
                }
            }
        }
        sort(cols.begin(), cols.end());
        int i = rows[rows.size() / 2];
        int j = cols[cols.size() / 2];
        auto f = [](vector<int>& arr, int x) {
            int s = 0;
            for (int v : arr) {
                s += abs(v - x);
            }
            return s;
        };
        return f(rows, i) + f(cols, j);
    }
};

Go

func minTotalDistance(grid [][]int) int {
	rows, cols := []int{}, []int{}
	for i, row := range grid {
		for j, v := range row {
			if v == 1 {
				rows = append(rows, i)
				cols = append(cols, j)
			}
		}
	}
	sort.Ints(cols)
	i := rows[len(rows)>>1]
	j := cols[len(cols)>>1]
	f := func(arr []int, x int) int {
		s := 0
		for _, v := range arr {
			s += abs(v - x)
		}
		return s
	}
	return f(rows, i) + f(cols, j)
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

Rust

impl Solution {
    #[allow(dead_code)]
    pub fn min_total_distance(grid: Vec<Vec<i32>>) -> i32 {
        let n = grid.len();
        let m = grid[0].len();

        let mut row_vec = Vec::new();
        let mut col_vec = Vec::new();

        // Initialize the two vector
        for i in 0..n {
            for j in 0..m {
                if grid[i][j] == 1 {
                    row_vec.push(i as i32);
                    col_vec.push(j as i32);
                }
            }
        }

        // Since the row vector is originally sorted, we only need to sort the col vector here
        col_vec.sort();

        Self::compute_manhattan_dis(&row_vec, row_vec[row_vec.len() / 2])
            + Self::compute_manhattan_dis(&col_vec, col_vec[col_vec.len() / 2])
    }

    #[allow(dead_code)]
    fn compute_manhattan_dis(v: &Vec<i32>, e: i32) -> i32 {
        let mut ret = 0;

        for num in v {
            ret += (num - e).abs();
        }

        ret
    }
}