DAY1P3.md

Where Will the Ball Fall

---

• Question:

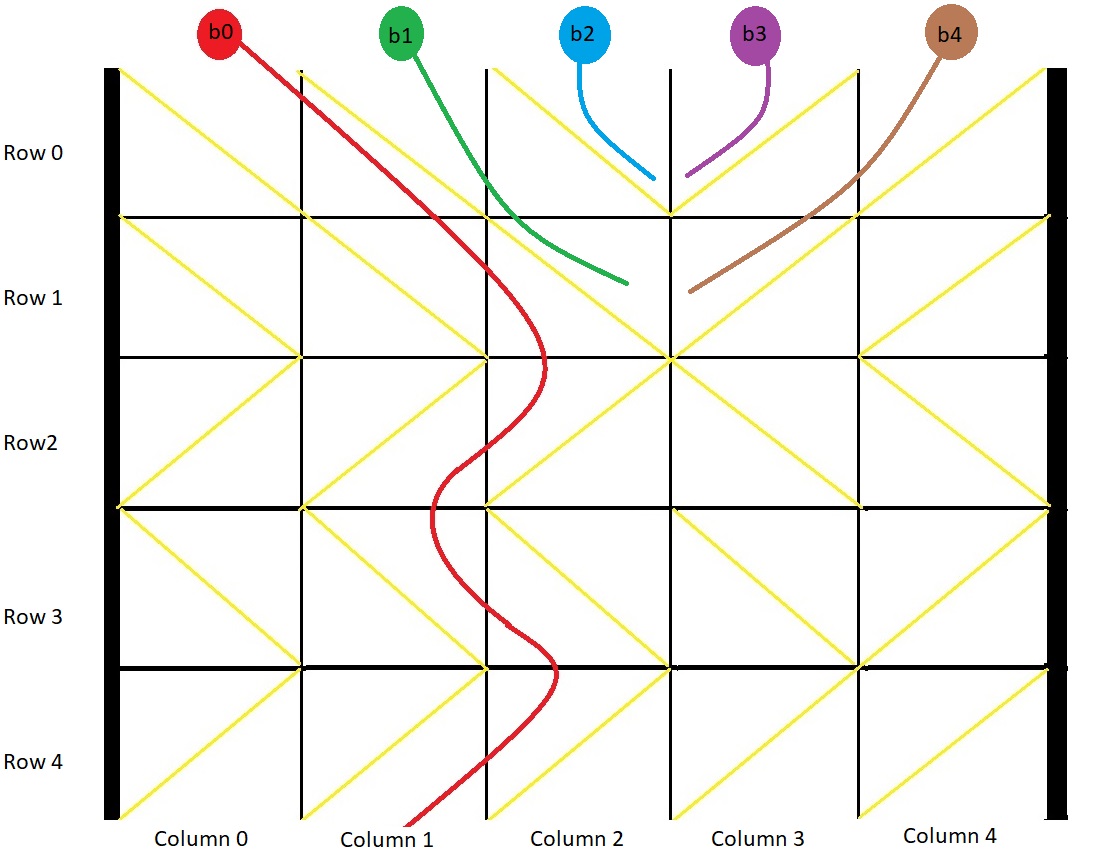
You have a 2-D grid of size m x n representing a box, and you have n balls. The box is open on the top and bottom sides.

Each cell in the box has a diagonal board spanning two corners of the cell that can redirect a ball to the right or to the left.

• A board that redirects the ball to the right spans the top-left corner to the bottom-right corner and is represented in the grid as 1.
• A board that redirects the ball to the left spans the top-right corner to the bottom-left corner and is represented in the grid as -1. We drop one ball at the top of each column of the box. Each ball can get stuck in the box or fall out of the bottom. A ball gets stuck if it hits a "V" shaped pattern between two boards or if a board redirects the ball into either wall of the box.

Return an array answer of size n where answer[i] is the column that the ball falls out of at the bottom after dropping the ball from the ith column at the top, or -1 if the ball gets stuck in the box.

---

• Example:

Input: grid = [[1,1,1,-1,-1],[1,1,1,-1,-1],[-1,-1,-1,1,1],[1,1,1,1,-1],[-1,-1,-1,-1,-1]]

Output: [1,-1,-1,-1,-1]

---

• Solution:

Code :

class Solution {
    public int dfs(int[][] grid, int i, int j){
        if(i==grid.length)
            return j;
        
        if(j<0 || j>=grid[0].length)
            return -1;
        
        if(grid[i][j]==1 && j+1<grid[0].length && grid[i][j+1]==1)
            return dfs(grid,i+1,j+1);
        
        else if(grid[i][j]==-1 && j-1>=0 && grid[i][j-1]==-1)
            return dfs(grid,i+1,j-1);
         
        return -1;
    }
    public int[] findBall(int[][] grid) {
        int m = grid[0].length;
        int[] ar = new int[m];
        
        for(int j=0;j<m;j++)
            ar[j]=dfs(grid,0,j);
        
        return ar;
    }
}