Skip to content

Latest commit

 

History

History
931 lines (719 loc) · 25.3 KB

二分查找.md

File metadata and controls

931 lines (719 loc) · 25.3 KB
Raw

二分查找

概述

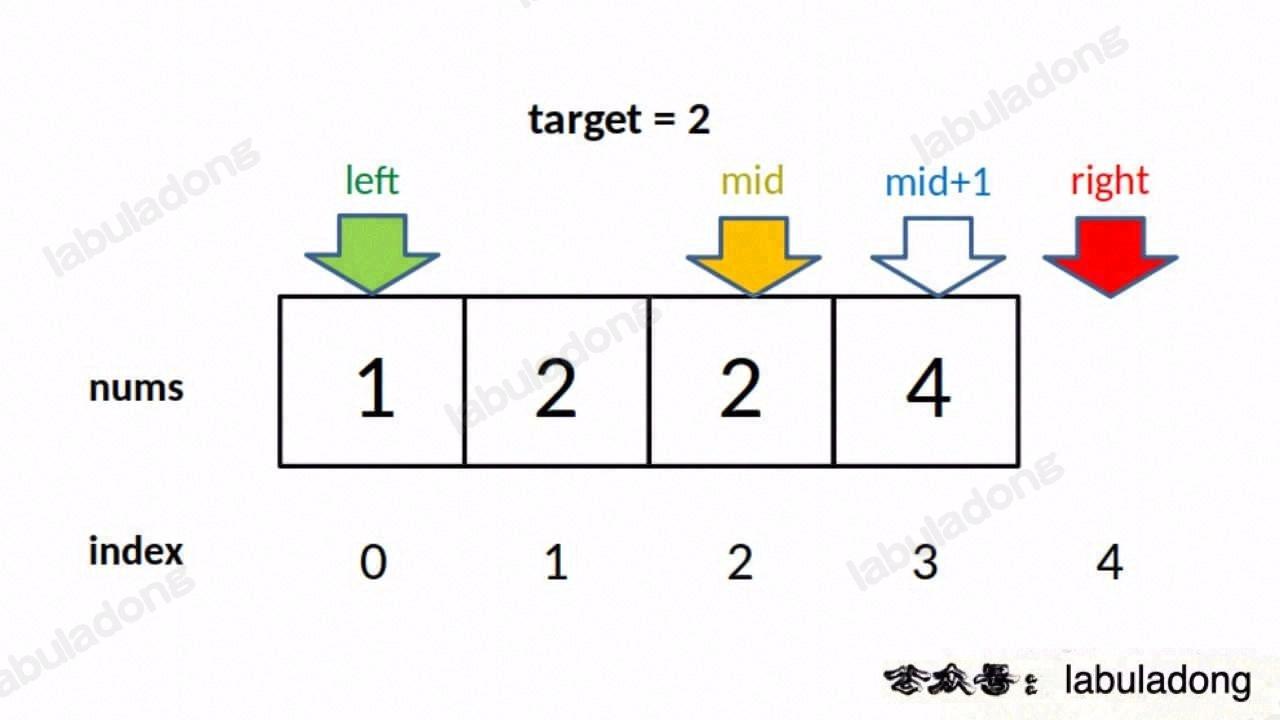
二分查找(Binary Search), 是一种在==有序数组中==查找目标元素的搜索算法。不过一般可以使用二分查找解决的也可以使用正向遍历解决，只是时间复杂度不一样

如果数组不是有序的就制造有序，例如使用 Arrays.sort(),或者拆分数组

  1. 先中中间元组开始，如果中间元素正好是目标元素，则返回
  2. 某一特定元素大于中间元素，就在中间元素的右边查找，同样从中间开始；如果小于中间元素，就在中间元素的左右查找，同样从中间开始
  3. 循环步骤 2，直到找到目标元素, 或者没找到返回特定值

二分法其实也是一种双指针

时间复杂度为 O(logn)，伪代码如下

lf = 0
rg = n - 1
while lf < rg
	mid = (lf + rg)/2
	if(arr[mid] == target)
		return mid
  else if(arr[mid] > target)
  	lf = mid + 1
  else
  	rg = mid - 1

引题

leetcode 704.二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

你可能会想到直接遍历

class Solution {
    public int search(int[] nums, int target) {
        for(int i = 0; i < nums.length; i++){
            if(target == nums[i]){
                return i;
            }
        }
        return -1;
    }
}

时间复杂度为 O(n)，而且忽略了一个重要的条件，就是有序数组。所以我们可以使用 二分法 将时间复杂度缩减为 O(logn)

class Solution {
    public int search(int[] nums, int target) {
        int lf = 0;
        int rg = nums.length - 1;
        while(lf <= rg){
            int mid = (lf + rg) / 2;
            if(nums[mid] == target){
                return mid;
            }else if(nums[mid] > target){
                rg = mid - 1;
            }else{
                lf = mid + 1;
            }
        }
        return -1;
    }
}

如果是 Python 想要向下取整使用 //

也无趣考虑整型溢出的问题，在 Python 中不区分 int 或者是 long

框架

二分法整体框架如下，这里只考虑有序数组

int binarySearch(int[] nums, int target) {
    int left = 0, right = ...;

    while(...) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            ...
        } else if (nums[mid] < target) {
            left = ...
        } else if (nums[mid] > target) {
            right = ...
        }
    }
    return ...;
}

在框架不变的情况下，有 3 大类基础模板

理解二分法的核心在于理解搜索区间

基础模板一

int binarySearch(int[] nums, int target){
  if(nums == null || nums.length == 0)
    return -1;

  int left = 0, right = nums.length - 1;
  while(left <= right){
    // Prevent (left + right) overflow
    int mid = left + (right - left) / 2;
    if(nums[mid] == target){ return mid; }
    else if(nums[mid] < target) { left = mid + 1; }
    else { right = mid - 1; }
  }

  // End Condition: left > right
  return -1;
}
  • 初始条件：left = 0, right = length-1
  • 终止：left <= right
  • 向左查找：right = mid-1
  • 向右查找：left = mid+1

为什么是 while(left <= right)

因为 right = nums.length - 1, 搜索区间为 [left,right] (left == right 是有意义的)

当 left == right + 1 时搜索区间为 [right + 1,right] 区间为空，显然这时候应该停止搜索，即 while(left <= right )

为什么是 left = mid + 1, right = mid - 1

关键是搜索区间，当 nums[mid] != target 的时候，下一步需要搜索那些区域呢？

因为区间是 [left,right]，所以应该搜索 [left,mid - 1] 和 [mid + 1,right]

当 nums[mid] < target 时应该搜索 [mid + 1,right] 所以让 left = mid + 1

当 nums[mid] > target 时应该搜索 [left,mid - 1] 所以让 right = mid - 1

基础模板二

int binarySearch(int[] nums, int target){
  if(nums == null || nums.length == 0)
    return -1;

  int left = 0, right = nums.length;
  while(left < right){
    // Prevent (left + right) overflow
    int mid = left + (right - left) / 2;
    if(nums[mid] == target){ return mid; }
    else if(nums[mid] < target) { left = mid + 1; }
    else { right = mid; }
  }

  // Post-processing:
  // End Condition: left == right
  if(left != nums.length && nums[left] == target) return left;
  return -1;
}
  • 初始条件：left = 0, right = length
  • 终止：left < right
  • 向左查找：right = mid
  • 向右查找：left = mid+1

为什么是 while(left < right)

Tips

如果 rg = nums.length 就使用 while(lf < rg)， 如果 rg = nums.length - 1 就使用 while(lf <= rg)

因为 right = nums.length, 搜索区间为 [left,right) (left == right 是没有意义的，数组取不到 right 下标的值)

当 left == right 时搜索区间为 [right,right) 区间为空，显然这时候应该停止搜索，即 while(left < right )

为什么是 left = mid + 1, right = mid

关键是搜索区间，当 nums[mid] != target 的时候，下一步需要搜索那些区域呢？

因为区间是 [left,right)，所以应该搜索 [left,mid)(其实也等价与模板一中的 [left,mid - 1]) 和 [mid + 1,right)

当 nums[mid] < target 时应该搜索 [mid + 1,right) 所以让 left = mid + 1

当 nums[mid] > target 时应该搜索 [left,mid) 所以让 right = mid

为什么需要 Post-processing

最后一次进入循环，分别指向了 left 和 right，而 mid 计算为 left

  1. nums[mid] == target 返回 mid
  2. nums[mid] > target 执行 right = mid 即 right = left，这种情况在最后一次循环中判断 nums[mid] == target 的时候已经判断过了
  3. nums[mid] < target 执行 left = mid + 1 即 left = right(最后一种情况)，这种情况没有判断过，所以需要额外一步判断 nums[left] 是否等于 target

例如 left = 2, right = 3，此时 mid = 2，如果 nums[mid] < target 就会执行 left = mid + 1，即 (left = 3) == right 循环终止，这样就不能判断 nums[3] 的情况了。所以需要在结尾判断 nums[left] 的值是否等于 target，而 left != nums.length 是因为数组越界是没有意义，所以无需判断

==模板 一二 的缺陷==

假设有一个有序数组 nums[1,2,2,2,3], target = 2

此时使用 模板 一二三 只会返回 2

但是如果我想得到 target 的左侧边界，即索引 1，或者我想得到 target 的右侧边界，即索引 3，这样的话此算法是无法处理的

所以这里就需要使用衍生模板

衍生模板 二分搜索左侧边界

在模板二的基础上往左搜索找到最左侧满足 target 的索引

int left_bound(int[] nums, int target) {
    int left = 0;
    int right = nums.length; // 注意
    
    while (left < right) { // 注意
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            right = mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid; // 注意
        }
    }
    return left;
}

当 nums[mid] == target 想往左搜索找到最左侧满足 target 的索引，区间为 [left,mid) 所以让 right = mid

int left_bound(int[] nums, int target) {
    int left = 0;
    int right = nums.length; // 注意
    
    while (left < right) { // 注意
        int mid = left + (right - left) / 2;
        if (nums[mid] >= target) {
            right = mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        }
    }
    return left;
}

为什么返回 left

其实返回 left 还是 right 都一样，因为终止条件为 left == right

如果 nums 中没有 target 怎么办

这就需要在模板的基础上加判断条件了

例如

1 1 2 2 3 target = 4
lf = 0 rg = 5 mid = 2
lf = 3 rg = 5 mid = 4
lf = 5 rg = 5

如果你这时候取 nums[left] 一定会越界，因为最后 left == right == nums.length，所以需要先判断一下是否越界(无需考虑 left < 0 的情况)

int left_bound(int[] nums, int target) {
    int left = 0;
    int right = nums.length; // 注意
    
    while (left < right) { // 注意
        int mid = left + (right - left) / 2;
        if (nums[mid] >= target) {
            right = mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        }
    }
    if(left >= nums.length)return -1;
    return nums[left] == target?left:-1;
}

基础模板一的衍生模板 二分搜索左侧边界

这里 nums[mid] == target 应该让 right = mid - 1，因为搜索区间是左闭区间

    int left_bound(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            if (nums[mid] == target) {
                right = mid - 1;
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] < target) {
                left = mid + 1;
            }
        }
        if (left >= nums.length) return -1;
        return nums[left] == target ? left : -1;
    }

衍生模板 二分搜索右侧边界

在模板二的基础上往右搜索找到最左侧满足 target 的索引

int right_bound(int[] nums, int target) {
    int left = 0, right = nums.length;
    
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            left = mid + 1; // 注意
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid;
        }
    }
    return left - 1; // 注意
}

当 nums[mid] == target 想往右搜索找到最右侧满足 target 的索引，区间为 [mid + 1,right) 所以让 left = mid + 1

int right_bound(int[] nums, int target) {
    int left = 0, right = nums.length;
    
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] <= target) {
            left = mid + 1; // 注意
        } else if (nums[mid] > target) {
            right = mid;
        }
    }
    return left - 1; // 注意
}

为什么返回 left - 1

同样的终止条件为 left == right，所以 right - 1 也可以，但是为什么减一呢？ 关键在 nums[mid] == target 的时候让 left = mid + 1

不管怎么样 left 都会往右移动到 mid + 1，即使 mid == target

if (nums[mid] == target) {
    left = mid + 1;

当移动后出现 left == right(考虑极值的情况) 这时结果明显应该是 mid，所以为了返回 mid，而返回 left - 1

img

如果 nums 中没有 target 怎么办

这就需要在模板的基础上加判断条件了, left - 1 是一定不会越界的，所以无需判断索引是否越界

int right_bound(int[] nums, int target) {
    int left = 0, right = nums.length;
    
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] <= target) {
            left = mid + 1; // 注意
        } else if (nums[mid] > target) {
            right = mid;
        }
    }
    return nums[left - 1] == target ? (left - 1) : -1;   
}

基础模板一的衍生模板 二分搜索右侧边界

这里 nums[mid] == target 应该让 left = mid + 1，因为搜索区间是左闭区间

    int right_bound(int[] nums, int target) {
        int left = 0, right = nums.length - 1;

        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            if (nums[mid] == target) {
                left = mid + 1;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid - 1;
            }
        }
        return nums[left - 1] == target ? (left - 1) : -1;
    }

框架小结

  1. 针对数值，为了方便记忆只考虑 right = nums.length - 1 的情况，即 while(left < right), left = mid + 1, right = mid - 1
  2. 如果是 while(left < right) 那么应该使用 right = mid，而 while(left <= right) 应该使用 right = mid + 1
  3. 非数组，是否是 while(left < right) 或者是 while(left <= right) 根据值是否有意义出发
  4. 返回值根据实际情况而定，通常会返回 mid 即 left - 1 或者是 rg + 1

lf + (rg - lf) / 2

你可能会在一些代码中看到 lf + (rg - lf)/2 来替代 (lf + rg) / 2

例如

class Solution {
    public int search(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = (right - left) / 2 + left;
            int num = nums[mid];
            if (num == target) {
                return mid;
            } else if (num > target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return -1;
    }
}

因为假设 lf 和 rg 都为 int 且当 rg 值为 Integer.MAX_VALUE 的时候， target 处于 (mid,rg) 之间

如果使用 (lf + rg)/2，lf + rg 可会溢出 int 的取值范围。按照分配律可以拆成 lf/2 + rg/2

但是因为在 Java 中如果被除数是奇数的话就会向下取整，所以不能直接使用 lf/2 + rg/2 会出现 drift ，例如

System.out.println(1/2 + 1/2); //0
System.out.println((1+1)/2); //1

而如果使用 lf + (rg - lf)/2

  1. lf 偶 rg 偶 值与 lf/2 + rg/2 相同，与 (lf + rg)/2 相同
  2. lf 偶 rg 奇 值与 lf/2 + rg/2 相同，与 (lf + rg)/2 相同
  3. lf 奇 rg 偶 值与 lf/2 + rg/2 相同，与 (lf + rg)/2 相同
  4. lf 奇 rg 奇 值与 lf/2 + rg/2 不同，与 (lf + rg)/2 相同

所以我们应该使用 lf + (rg - lf)/2 替代 (lf + rg)/2

进一步，我们还可以使用位运算来提升效率，即 lf + ((rg - lf) >> 1)

这里需要使用 ((rg -lf) >> 1) 因为位运算在所有的编程语言中优先级都是最低的

例题

0x01 69. x 的平方根

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

**注意：**不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例 1：

输入：x = 4
输出：2

示例 2：

输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

当然可以使用一次遍历

class Solution {
    public int mySqrt(int x) {
        int res = 0;
        if(x == 0)return 0;
        for(int i = 1;i <= x/i;i++){
            res = i;
        }
        return res;
    }
}

但是按照时间复杂度应该优先使用二分

class Solution {
    public int mySqrt(int x) {
        int lf = 0, rg = x;
        int res = -1;
        while(lf <= rg){
            int mid = lf + (rg - lf)/2;
            if((long)mid*mid == x){
                return mid;
            }else if((long)mid*mid > x){
                rg = mid - 1;
            }else{
                res = mid;
                lf = mid + 1;
            }
        }
        return res;
    }
}

实际并不需要 res 这个值，所以整理代码可得

class Solution {
    public int mySqrt(int x) {
        int lf = 0, rg = x;
        while(lf <= rg){
            int mid = lf + ((rg - lf)>>1);
            if((long)mid*mid == x){
                return mid;
            }else if((long)mid*mid > x){
                rg = mid - 1;
            }else{
                lf = mid + 1;
            }
        }
        return rg;
    }
}

当然也可以写成这样

class Solution {
    public int mySqrt(int x) {
        int lf = 0, rg = x;
        if(x == 0){
            return 0;
        }
        if(x == 1){
            return 1;
        }
        while(lf <= rg){
            int mid = lf + ((rg - lf)>>1);
            if(mid > x / mid){
                rg = mid - 1;
            }else if (mid < x / mid){
                lf = mid + 1;
            }else{
                return mid;
            }
        }
        return rg;
    }
}

为什么是 while(lf <= rg)

这里使用 lf <= rg 是因为搜索区间可以是 [0,x],即极端情况下，例如 0 和 1 都是有意义的，指针必须走到等等的情况

为什么返回 rg

因为如果在最后一种情况中，即 rg == lf，可以推出 mid == rg == lf，如果没有找到 mid*mid == x 的情况下，mid*mid 的值一定是最接近 x 的(不管是大于还是小于)

最后一种情况是 mid*mid > x 一定类似下图

#before
      lf(rg) 
      | 
      v
      ^
      |
     mid
     
#after
rg   lf
|    |	
v 	 v
		 ^
		 |
		mid

要求小于 x 可以推出返回值可以是

  1. rg
  2. lf - 1
  3. mid - 1

最后一种情况是 mid*mid < x 一定类似下图

#before      
      lf(rg) 
      | 
      v
      ^
      |
     mid
     
#after
     rg   lf 
     |	  |
  	 v    v
		 ^
		 |
		mid

要求小于 x 可以推出返回值可以是

  1. rg
  2. mid
  3. lf - 1

合并两项，可以得出返回值可以是 rg 或者是 lf - 1

0x02 33. 搜索旋转排序数组

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

假设将一个数组对半，一定有 2 种情况

  1. 左边的部分是有序的，可以使用二分法；右边是无序的，但是也可以对半，重新判断
  2. 右边的部分是有序的，可以使用二分法；左边是无序的，但是也可以对半，重新判断
class Solution {
    public int search(int[] nums, int target) {
        int lf = 0,rg = nums.length - 1;
        while(lf <= rg){
            int mid = lf + ((rg - lf)>>1);
            if(nums[mid] == target){
                return mid;
            }else if(nums[mid] >= nums[0]){
                //mid 左侧是有序的, 判断 target 是否在区间内
                if(nums[0] < target && target < nums[mid]){
                    rg = mid - 1;
                }else{
                    lf = mid + 1;
                }
            }else if(nums[mid] < nums[0]){
                //mid 右侧是有序的，判断 target 是否在区间内
                if(nums[mid] < target && target < nums[rg]){
                    lf = mid + 1;
                }else{
                    rg = mid - 1;
                }
            }
        }
        return -1;
    }
}

但是这里并不是完整的，当 target 处于边界的时候，即 0 或者是 nums.length - 1 的情况

假设输入的是 [1,3,5] target = 1，左边界就会往右移动，显然不对，所以条件应该为 if(nums[0] <= target && target < nums[mid])

输入 [5,1,3] target = 3 同理 if(nums[mid] < target && target <= nums[rg])

0x03 剑指 Offer 53 在排序数组中查找数字

统计一个数字在排序数组中出现的次数。

示例 1:

输入: nums = [5,7,7,8,8,10], target = 8
输出: 2

示例 2:

输入: nums = [5,7,7,8,8,10], target = 6
输出: 0

你当然可以一次遍历，但是同样的没有使用到升序的条件

class Solution {
    public int search(int[] nums, int target) {
        int res = 0;
        for(int i = 0;i < nums.length;i++){
            if(target == nums[i]){
                res++;
            }
        }
        return res;
    }
}

但是也可以使用二分法

先确认基本框架

class Solution {
    public int search(int[] nums, int target) {
        int lf = 0;
        int rg = nums.length - 1;
        int res = 0;
        while(lf < rg){
            int mid = lf + (rg - lf)/2;
            if(target == nums[mid]){
                res++;
            }else if(target < nums[mid]){
                rg = mid - 1;
            }else{
                lf = mid + 1;
            }
        }
        return res;
    }
}

这里还有问题，就是当 target == nums[mid] 的时候，lf 和 rg 都没有移动，所以会出现死循环

仔细分析一些题干，因为是升序的，所以就是找第一个等于 target 的下标作为 lf，第一个大于 target 的下标作为 rg，就可以退出一共有多少个 target，为 rg - lf + 1

0x04 162. 寻找峰值

峰值元素是指其值严格大于左右相邻值的元素。

给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞ 。

你必须实现时间复杂度为 O(log n) 的算法来解决此问题。

示例 1：

输入：nums = [1,2,3,1]
输出：2
解释：3 是峰值元素，你的函数应该返回其索引 2。

示例 2：

输入：nums = [1,2,1,3,5,6,4]
输出：1 或 5 
解释：你的函数可以返回索引 1，其峰值元素为 2；
     或者返回索引 5， 其峰值元素为 6。

可以使用一次遍历，找出最大值，最大值一定是峰值

class Solution {
    public int findPeakElement(int[] nums) {
       int p = 0;
       for(int i = 0; i < nums.length; i++){
           if(nums[i] > nums[p]){
               p = i;
           }
       }
       return p;
    }
}

但是时间复杂度为 O(n)

因为 nums[-1] = nums[n] = -∞，如果 nums[mid] > nums[mid + 1] 说明当前值可能是一个峰值，或者沿着它一定可以找到一个峰值，所以可以把 rg 移动到 mid，比较 [lf,mid]

如果 nums[mid] < nums[mid + 1] 那就说明当前值一定不是一个峰值，所以把 lf 移动到 mid + 1

class Solution {
    public int findPeakElement(int[] nums) {
        int lf = 0,rg = nums.length - 1;
        //防止越界
        while(lf < rg){
            int mid = lf + ((rg - lf)>>1);
            if(nums[mid] <= nums[mid + 1]){
                lf = mid + 1;
            }else{
                rg = mid;
            }
        }
        //不管返回 lf 或者是 rg 都一样
        return rg;
    }
}

0x05 153. 寻找旋转排序数组中的最小值

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

  • 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
  • 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

示例 2：

输入：nums = [4,5,6,7,0,1,2]
输出：0
解释：原数组为 [0,1,2,4,5,6,7] ，旋转 4 次得到输入数组。

当然可以使用 O(n) 遍历出结果

class Solution {
    public int findMin(int[] nums) {
        int p = 0;
        for(int i = 0; i < nums.length; i++){
            if(nums[i] < nums[p]){
                p = i;
            }
        }
        return nums[p];
    }
}

使用二分法更加简便

class Solution {
    public int findMin(int[] nums) {
        int lf = 0,rg = nums.length - 1;
        while(lf < rg){
            int mid = lf + ((rg - lf)>>1);
            if(nums[mid] <= nums[rg]){
                rg = mid;
            }else{
                lf = mid + 1;
            }          
        }
        return nums[rg];
    }
}

references

  1. [^https://labuladong.github.io/algo/di-ling-zh-bfe1b/wo-xie-le--3c789/]
  2. [^https://leetcode.cn/leetbook/read/binary-search/x6q6fi/]
  3. [^https://programmercarl.com/0704.%E4%BA%8C%E5%88%86%E6%9F%A5%E6%89%BE.html#%E6%80%9D%E8%B7%AF]
  4. [^https://leetcode.cn/problems/binary-search/solutions/8337/er-fen-cha-zhao-xiang-jie-by-labuladong/]