Machine Learning Concepts

Table of content

Machine Learning Concepts

Data Preprocessing

Normalization and Standardization

(歸一化)

Normalization/standardization are designed to achieve a similar goal, which is to create features that have similar ranges to each other and widely used in data analysis to help the programmer to get some clue out of the raw data.

What is the difference between normalization, standardization, and regularization for data?
Differences between normalization, standardization and regularization
如何理解Normalization，Regularization 和 standardization？

When do we need normalization?

In practice, when a model is solved by gradient descent, then its input data basically needs to be normalized. (but this is not necessary for a decision tree model, because the information gain doesn't affect by normalization)

Feature Scaling

aka. Data Normalization (generally performed during the data preprocessing step)

A method used to standardize the range of independent variables or features of data

Normalization (Min-Max Scaling)

In Algebra, Normalization seems to refer to the dividing of a vector by its length and it transforms your data into a range between 0 and 1

e.g. Rescalse feature to [0, 1]

$$ x^{\prime}=\frac{x-\min (x)}{\max (x)-\min (x)} $$

e.g. Rescale feature to [−1, 1]

$$ x^{\prime}=\frac{x-m e a n(x)}{\max (x)-\min (x)} $$

Standardization (Z-Score Normalization)

rescale the features to zero-mean and unit-variance

And in statistics, Standardization seems to refer to the subtraction of the mean and then dividing by its SD (standard deviation). Standardization transforms your data such that the resulting distribution has a mean of 0 and a standard deviation of 1.

$$ x^{\prime}=\frac{x-\mu}{\sigma} $$

Example of SVM

SVM is better to normalize data between -1 and 1

This is a common problem in SVM, for example. I tend to use "normalization" when I map the features into [-1,1] by dividing (i.e. "normalizing") by the largest values in the sample and "standarization" when I convert to z-score (i.e. standard deviations from the mean value of the sample).

Sampling for Unbalanced Data

To deal with unbalanced/skewed data, we need some sampling techanique to balance this problem.

Wiki - Oversampling and undersampling in data analysis

Under-sampling

Use the less amount label data as the maximum sampling number for other class

Over-sampling

Reuse the same data of the less amount label data

SMOTE: Synthetic Minority Over-sampling Technique

Missing Value

Scikit Learn - 4.4 Imputation of missing values
How to Handle Missing Data

Options

Use the feature’s mean value from all the available data.
Fill in the unknown with a special value like -1.
Ignore the instance.
Use a mean value from similar items.
Use another machine learning algorithm to predict the value.

Dimensionality Reduction

Background

The relevant features may not be explicitly presented in the data.
We have to identify the relevant features before we can begin to apply other machine learning algorithm

The reasons we want to simplify our data

Making the dataset easier to use
Reducing computational cost of many algorithms
Removing noise
Making the results easier to understand

Factor Analysis

We assume that some unobservable latent variables are generating the data we observe.
The data we observe is assumed to be a linear combination of the latent variables and some noise
The number of latent variables is possibly lower than the amount of observed data, which gives us the dimensionality reduction

ICA

ICA stands for Independent Component Analysis

ICA assumes that the data is generated by N sources, which is similar to factor analysis.
The data is assumed to be a mixture of observations of the sources.
The sources are assumed to be statically independent, unlike PCA, which assumes the data is uncorrelated.
If there are fewer sources than the amount of our observed data, we'll get a dimensionality reduction.

PCA vs SVD

PCA
- find the eigenvalues of a matrix
  - these eigenvalues told us what features were most important in our data set
SVD
- find the singular values in $\Sigma$
  - singular values and eigenvlues are related
  - singular vlues are the square root of the eigenvlues of $AA^T$

Label Encoding

Scikit Learn - 4.9 Transforming the prediction target (y)

Classification Imbalance

To alter the data used to train the classifier to deal with imbalanced classification tasks.

Oversample: means to duplicate examples
Undersample: means to delete examples

Scenario

You want to preserve as much information as possible about the rare case (e.g. Credit card fraud)
- Keep all of the examples form the positive class
- Undersample or discard examples form the negative class

Drawback

Deciding which negaive examples to toss out. (You may throw out examples which contain valuable information)

Solution

To pick samples to discard that aren't near the decision boundary
Use a hybrid approach of undersampling the negative class and oversampling the positive class

(Oversample the positive class have some approaches)

Replicate the existing examples
Add new points similar to the existing points
Add a data point interpolated between existing data points (can lead to overfitting)

Model Expansion

Binary to Multi-class

Wiki - Multiclass classification
pdf - Lecture 18: Multiclass Support Vector Machines

While some classification algorithms naturally permit the use of more than two classes, others are by nature binary algorithms; these can, however, be turned into multinomial classifiers by a variety of strategies.

Main Ideas

Decompose the multiclass classification problem into multiple binary classification problems
Use the majority voting principle (a combined decision from the committee) to predict the label

One-vs-rest (one-vs-all) Approaches

Tutorial:

Lecture 6.7 — Logistic Regression | MultiClass Classification OneVsAll — [Andrew Ng]

Pairwise (one-vs-one, all-vs-all) Approaches

Model Validation

Splitting Data

Training Set: to get weights (parameters) by training
Validation Set / Development Set: to determine superparameters and when to stop training (early stop)
Test Set: to evaluate performance

Simplest Split

Split data into Training and Test set (usually 2:1)

Problem: the sample might not be representative

Hold-out Validation

Stratification: sampling for training and testing within classes (this ensures that each class is represented with approximately equal proportions in both subsets)

N-Fold Cross-Validation (Repeated Hold-out)

Repeat hold-out process with different subsamples

Start with a dataset D of labeled sample
Randomly partiiton into N groups (i.e. N-fold)
Calculate average n errors

Hold-one-out Cross-Validation (LOO CV)

Train-Validation-Test

Split the Train data into Traintrain and Validation

Use the validation set to find the best parameters
Use the test set to estimate the true error

Nested N-Fold Cross-Validation

Bootstrapping

The bootstrap is an estimaiton method that uses sampling with replacement to form the training set

Case where bootstrap does not apply

Too small datasets: the original sample is not a good approximation of the population
Dirty data: outliers add variability in our estimations
Dependence structures (e.g. time series, spatial problems): bootstrap is based on the assumption of independence

0.632-bootstrap

$$ \lim_{n \rightarrow \infty} (1-\frac{1}{n})^n = \frac{1}{e} = 0.368 $$

This means that the training data will contain approximately 63.2% of the examples.

Model Evaluation

CSDN - 深度學習多種模型評估指標介紹 - 附sklearn實現

Classification

Accuracy (Error Rate)

The error rate = the number of misclassified instances / the total number of instances tested.
Measuring errors this way hides how instances were misclssified.

Confusion Matrix

Wiki - Confusion Matrix

With a confusion matrix you get a better understanding of the classification errors.
If the off-diagonal elements are all zero, then you have a perfect classifier
Construct a confusion matrix: a table about Actual labels vs. Predicted label

Precision, Recall Ratio

These metrics that are more useful than error rate when detection of one class is more important than another class.

Consider a two-class problem. (Confusion matrix with different outcome labeled)

Actual \ Redicted	+1	-1
+1	True Positive (TP)	False Negative (FN)
-1	False Positive (FP)	True Negative (TN)

Precision = TP / (TP + FP)
- Tells us the fraction of records that were positive from the group that the classifier predicted to be positive
Recall = TP / (TP + FN)
- Measures the fraction of positive examples the classifier got right.
- Classifiers with a large recall dont have many positive examples classified incorectly.
F₁ Score = 2 × (Precision × Recall) / (Precision + Recall)

Summary:

You can easily construct a classifier that achieves a high measure of recall or precision but not both.
If you predicted everything to be in the positive class, you'd have perfect recall but poor precision.

Now consider multiple classes problem.

Macro-average
Micro-average

ROC curve

Wiki - Receiver operating characteristic

ROC stands for Receiver Operating Characteristic

The ROC curve shows how the two rates chnge as the threshold changes
The ROC curve has two lines, a solid one and a dashed one.
- The solid line:
  - the leftmost point corresponds to classifying everything as the negative class.
  - the rightmost point corresponds to classifying everything in the positive class.
- The dashed line:
  - the curve you'd get by randomly guessing.
The ROC curve can be used to compare classifiers and make cost-versus-benefit decisions.
- Different classifiers may perform better for different threshold values
The best classifier would be in upper left as much as possible.
- This would mean that you had a high true positive rate for a low false positive rate.

AUC (Area Under the Curve): A metric to compare different ROC

The AUC gives an average value of the classifier's performance and doesn't substitute for looking at the curve.
A perfect classifier would have an AUC of 1.0, and random guessing will give you a 0.5.

Regression

Mean Absolute Error (MAE)

Mean Squared Error (MSE)

Root Mean Squared Error (RMSE)

Clustering

Within Groups Sum of Squares

Elbow method

Mean Silhouette Coefficient of all samples

Calinski and Harabaz score

Max score => the best number of groups (clustes)

Fitting and Model Complexity

Sample Complexity: A more complex function requires more data to generate an accurate model.

Generalization

A good learning program learns something about the data beyond the specific cases that have been presented to it
Classifier can minimize "i.i.d" error, that is error over future cases (not used in training). Such cases contain both previously encountered as well as new cases.

Error

Training error: error on training set
Generalization error: expected value of the errors on testing data
- Capacity: ability to fit a wide variety of functions (the expressive power)
  - too low (underfitting): struggle to fit the training set
  - too high (overfitting): overfit by memorizing properties of the training set that do not serve them well on the test set

Overfitting

In general, over-fitting a model to the data means that we learn non-representative properties of the sample data

overfitting and poor generalization are synonymous as long as we've learned the training data well.

Overfitting is affected by

the "simplicity" of the classifier (e.g. straight vs. wiggly line)
the size of the dataset => too small
the complexity of the function we wish to learn from data
the amount of noise
the number of the variable (features)

Low training set error rate but high validation set error rate

To reduce the chance of overfitting

Simplify the model
- e.g. non-linear model => linear model
Add constraint element to reduce hypothesis space
- e.g. L1/L2 norm
Boosting method
Dropout hyperparameter

Underfitting

High training set error rate

Occam's Razor Principle

Wiki - Occam's razor

Law of Parsimony

Regularization (Weight Decay)

Used to control the complexity of the model (in case of overfitting)

Regularization (mathematics)

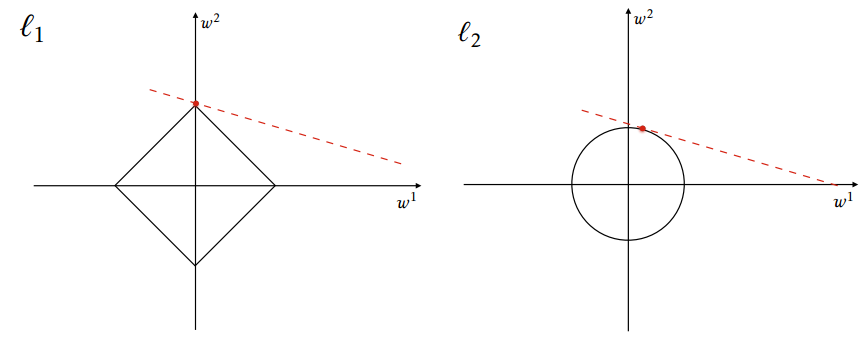
Regularization is a technique to avoid overfitting when training machine learning algorithms. If you have an algorithm with enough free parameters you can interpolate with great detail your sample, but examples coming outside the sample might not follow this detail interpolation as it just captured noise or random irregularities in the sample instead of the true trend. Overfitting is avoided by limiting the absolute value of the parameters in the model. This can be done by adding a term to the cost function that imposes a penalty based on the magnitude of the model parameters. If the magnitude is measured in L1 norm this is called "L1 regularization" (and usually results in sparse models), if it is measured in L2 norm this is called "L2 regularization", and so on.

Example 1: let $\theta = (w_1, w_2, \dots, w_n)$ as model parameters
Example 2: The original loss function is denoted by $f(x)$, and the new one is $F(x)$.
- Where ${\lVert x \rVert}p = \sqrt[p]{\sum{i = 1}^{n} {\lvert x_i \rvert}^p}$

L1 Regularization (lasso)

$R(\theta) = ||\theta ||_1 = |w_1| + |w_2| + \cdots + |w_n|$
$F(x)=f(x)+\lambda|x|_{1}$

L2 Regularization (ridge regression)

$R(\theta) = ||\theta ||_2^2 = w_1^2 + w_2^2 + \cdots + w_n^2$
$F(x) = f(x) + \lambda {\lVert x \rVert}_2^2$
Understanding the scaling of L² regularization in the context of neural networks

L1+L2 Regularization

$R(\theta) = \alpha ||\theta ||_1 + (1-\alpha) ||\theta ||_2^2$

Reducing Loss

Common Loss Function

Hinge Loss

Binary classification

$$ L_{\text{hinge}}(\hat{y}, y) = \max(0, 1-y \cdot \hat{y}) $$

Multi-class classification

$$ L_{\text{hinge}}(\hat{y}, y) = \max(0, 1- (\hat{y}_t - \hat{y}_k) $$

Cross Entropy Loss (Negative Log Likelihood)

Used to measure the similarity between two probability distribution.

$$ H(p, q) = - \sum_x p(x) log q(x) $$

$p(x)$ represents the real distribution.
$q(x)$ represents the model/estimate distribution.