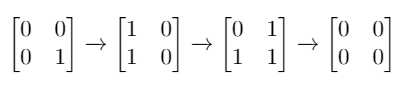1284

1284. Minimum Number of Flips to Convert Binary Matrix to Zero Matrix (Hard)

Given a m x n binary matrix mat. In one step, you can choose one cell and flip it and all the four neighbors of it if they exist (Flip is changing 1 to 0 and 0 to 1). A pair of cells are called neighbors if they share one edge.

Return the minimum number of steps required to convert mat to a zero matrix or -1 if you cannot.

A binary matrix is a matrix with all cells equal to 0 or 1 only.

A zero matrix is a matrix with all cells equal to 0.

 

Example 1:

Input: mat = [[0,0],[0,1]]
Output: 3
Explanation: One possible solution is to flip (1, 0) then (0, 1) and finally (1, 1) as shown.

Example 2:

Input: mat = [[0]]
Output: 0
Explanation: Given matrix is a zero matrix. We do not need to change it.

Example 3:

Input: mat = [[1,0,0],[1,0,0]]
Output: -1
Explanation: Given matrix cannot be a zero matrix.

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 3
• mat[i][j] is either 0 or 1.

Companies:
Google

Related Topics:
Array, Bit Manipulation, Breadth-First Search, Matrix

Similar Questions:

• Minimum Operations to Remove Adjacent Ones in Matrix (Hard)
• Remove All Ones With Row and Column Flips (Medium)

Solution 1. Bit Mask + BFS

// OJ: https://leetcode.com/problems/minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix/
// Author: github.com/lzl124631x
// Time: O(MN * 2^(MN))
// Space: O(2^(MN))
class Solution {
public:
    int minFlips(vector<vector<int>>& A) {
        int M = A.size(), N = A[0].size(), init = 0, step = 0, dirs[4][2] = {{0,1},{0,-1},{1,0},{-1,0}};
        for (int i = 0; i < M; ++i) {
            for (int j = 0; j < N; ++j) init |= A[i][j] << (i * N + j);
        }
        queue<int> q{{init}};
        unordered_set<int> seen{init};
        auto flip = [&](int &state, int x, int y) { state ^= 1 << (x * N + y); };
        while (q.size()) {
            int cnt = q.size();
            while (cnt--) {
                int u = q.front();
                q.pop();
                if (u == 0) return step;
                for (int i = 0; i < M; ++i) {
                    for (int j = 0; j < N; ++j) {
                        int v = u;
                        flip(v, i, j);
                        for (auto &[dx, dy] : dirs) {
                            int a = i + dx, b = j + dy;
                            if (a < 0 || b < 0 || a >= M || b >= N) continue;
                            flip(v, a, b);
                        }
                        if (seen.count(v)) continue;
                        seen.insert(v);
                        q.push(v);
                    }
                }
            }
            ++step;
        }
        return -1;
    }
};