|
| 1 | + |
| 2 | +## 题目地址(3347. 执行操作后元素的最高频率 II - 力扣(LeetCode)) |
| 3 | + |
| 4 | +https://leetcode.cn/problems/maximum-frequency-of-an-element-after-performing-operations-ii/description/ |
| 5 | + |
| 6 | +## 题目描述 |
| 7 | + |
| 8 | + <p>给你一个整数数组 <code>nums</code> 和两个整数 <code>k</code> 和 <code>numOperations</code> 。</p> |
| 9 | + |
| 10 | +<p>你必须对 <code>nums</code> 执行 <strong>操作</strong> <code>numOperations</code> 次。每次操作中,你可以:</p> |
| 11 | + |
| 12 | +<ul> |
| 13 | + <li>选择一个下标 <code>i</code> ,它在之前的操作中 <strong>没有</strong> 被选择过。</li> |
| 14 | + <li>将 <code>nums[i]</code> 增加范围 <code>[-k, k]</code> 中的一个整数。</li> |
| 15 | +</ul> |
| 16 | + |
| 17 | +<p>在执行完所有操作以后,请你返回 <code>nums</code> 中出现 <strong>频率最高</strong> 元素的出现次数。</p> |
| 18 | + |
| 19 | +<p>一个元素 <code>x</code> 的 <strong>频率</strong> 指的是它在数组中出现的次数。</p> |
| 20 | + |
| 21 | +<p> </p> |
| 22 | + |
| 23 | +<p><strong class="example">示例 1:</strong></p> |
| 24 | + |
| 25 | +<div class="example-block"> |
| 26 | +<p><span class="example-io"><b>输入:</b>nums = [1,4,5], k = 1, numOperations = 2</span></p> |
| 27 | + |
| 28 | +<p><span class="example-io"><b>输出:</b>2</span></p> |
| 29 | + |
| 30 | +<p><strong>解释:</strong></p> |
| 31 | + |
| 32 | +<p>通过以下操作得到最高频率 2 :</p> |
| 33 | + |
| 34 | +<ul> |
| 35 | + <li>将 <code>nums[1]</code> 增加 0 ,<code>nums</code> 变为 <code>[1, 4, 5]</code> 。</li> |
| 36 | + <li>将 <code>nums[2]</code> 增加 -1 ,<code>nums</code> 变为 <code>[1, 4, 4]</code> 。</li> |
| 37 | +</ul> |
| 38 | +</div> |
| 39 | + |
| 40 | +<p><strong class="example">示例 2:</strong></p> |
| 41 | + |
| 42 | +<div class="example-block"> |
| 43 | +<p><span class="example-io"><b>输入:</b>nums = [5,11,20,20], k = 5, numOperations = 1</span></p> |
| 44 | + |
| 45 | +<p><span class="example-io"><b>输出:</b>2</span></p> |
| 46 | + |
| 47 | +<p><strong>解释:</strong></p> |
| 48 | + |
| 49 | +<p>通过以下操作得到最高频率 2 :</p> |
| 50 | + |
| 51 | +<ul> |
| 52 | + <li>将 <code>nums[1]</code> 增加 0 。</li> |
| 53 | +</ul> |
| 54 | +</div> |
| 55 | + |
| 56 | +<p> </p> |
| 57 | + |
| 58 | +<p><strong>提示:</strong></p> |
| 59 | + |
| 60 | +<ul> |
| 61 | + <li><code>1 <= nums.length <= 10<sup>5</sup></code></li> |
| 62 | + <li><code>1 <= nums[i] <= 10<sup>9</sup></code></li> |
| 63 | + <li><code>0 <= k <= 10<sup>9</sup></code></li> |
| 64 | + <li><code>0 <= numOperations <= nums.length</code></li> |
| 65 | +</ul> |
| 66 | + |
| 67 | +## 前置知识 |
| 68 | + |
| 69 | +- 二分 |
| 70 | + |
| 71 | +## 公司 |
| 72 | + |
| 73 | +- 暂无 |
| 74 | + |
| 75 | +## 思路 |
| 76 | + |
| 77 | +容易想到的是枚举最高频率的元素的值 v。v 一定是介于数组的最小值 - k 和最大值 + k 之间的。因此我们可以枚举所有可能得值。但这会超时。可以不枚举这么多么?答案是可以的。 |
| 78 | + |
| 79 | +刚开始认为 v 的取值一定是 nums 中的元素值中的一个,因此直接枚举 nums 即可。但实际上是不对的。比如 nums = [88, 53] k = 27 变为 88 或者 53 最高频率都是 1,而变为 88 - 27 = 61 则可以使得最高频率变为 2。 |
| 80 | + |
| 81 | +那 v 的取值有多少呢?实际上除了 nums 的元素值,还需要考虑 nums[i] + k, nums[i] - k。为什么呢? |
| 82 | + |
| 83 | +数形结合更容易理解。 |
| 84 | + |
| 85 | +如下图,黑色点表示 nums 中的元素值,它可以变成的值的范围用竖线来表示。 |
| 86 | + |
| 87 | +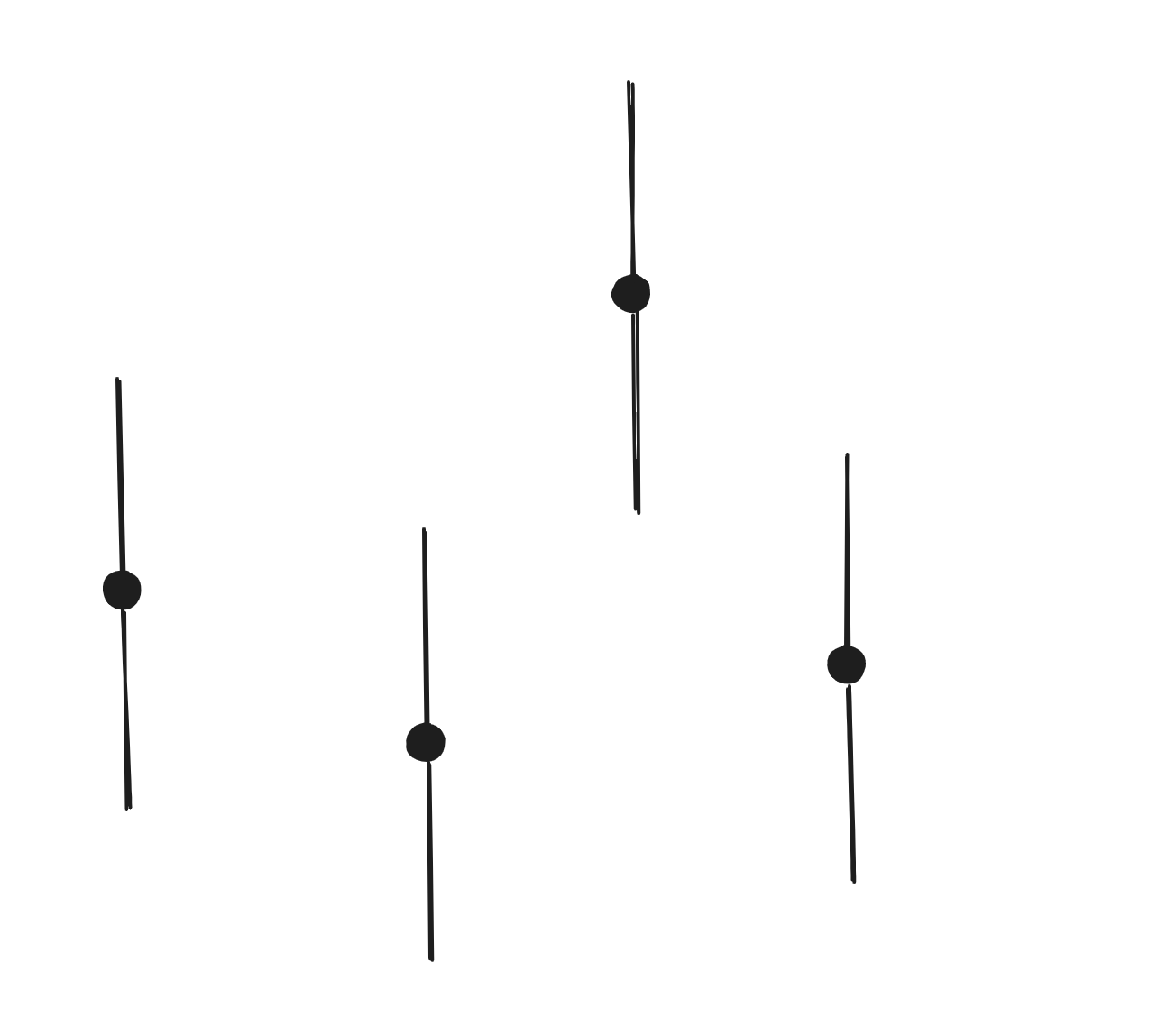 |
| 88 | + |
| 89 | +如果两个之间有如图红色部分的重叠区域,那么就可以通过一次操作使得二者相等。当然如果两者本身就相等,就不需要操作。 |
| 90 | + |
| 91 | +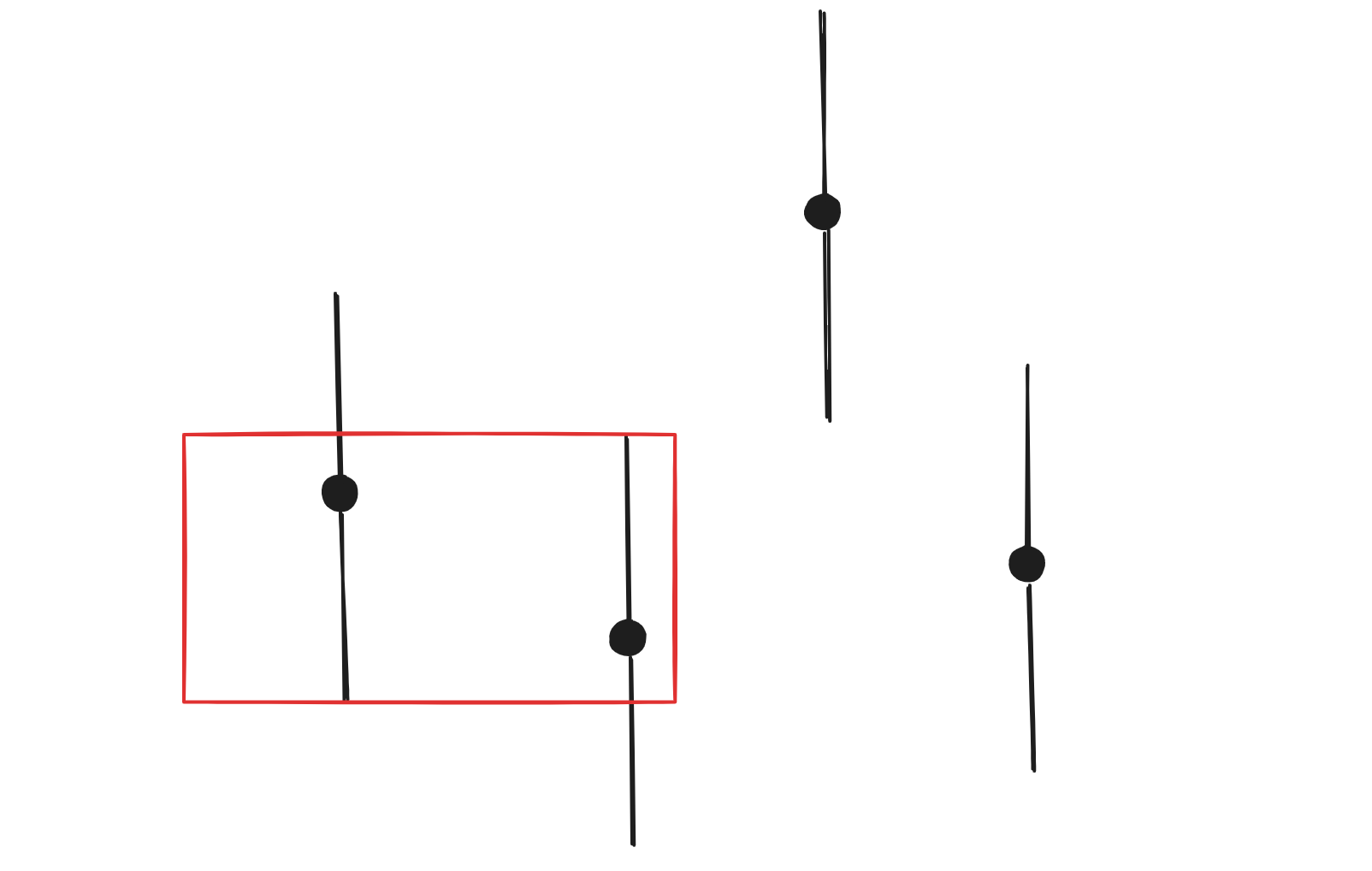 |
| 92 | + |
| 93 | +如上图,我们可以将其中一个数变成另外一个数。但是如果两者是下面的关系,那么就不能这么做,而是需要变为红色部分的区域才行。 |
| 94 | + |
| 95 | +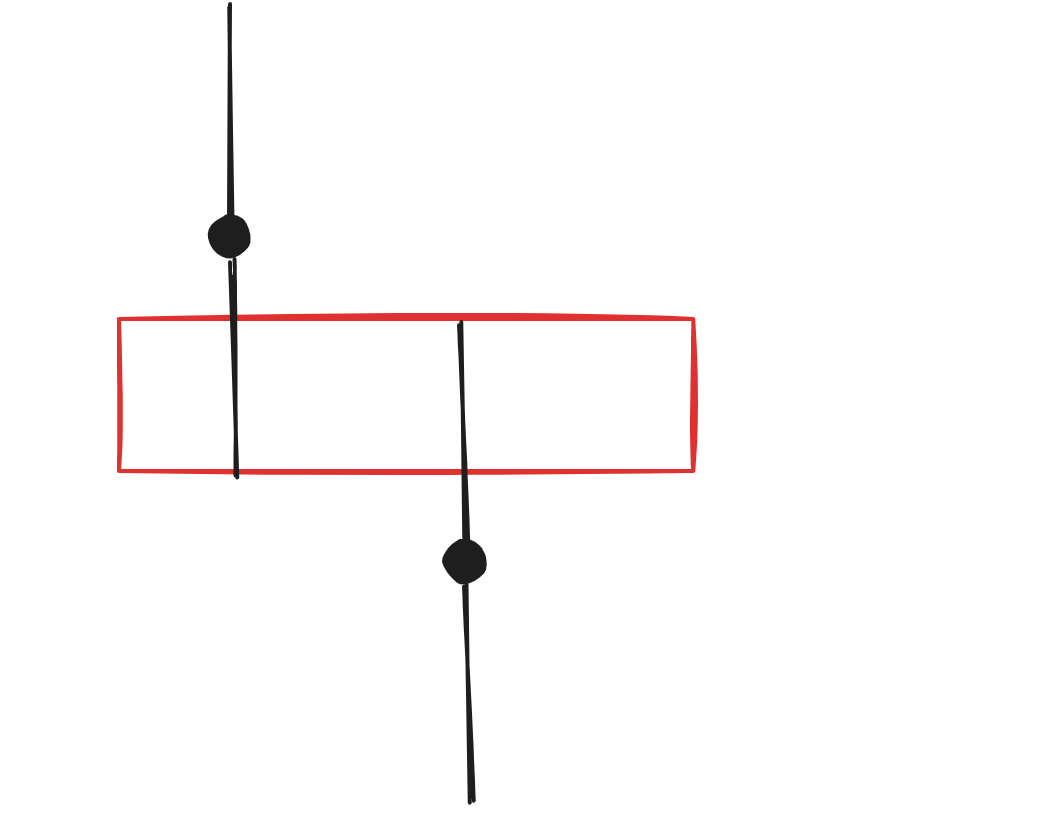 |
| 96 | + |
| 97 | +如果更进一步两者没有相交的红色区域,那么就无法通过操作使得二者相等。 |
| 98 | + |
| 99 | + |
| 100 | + |
| 101 | +最开始那种朴素的枚举,我们可以把它看成是一个红线不断在上下移动,不妨考虑从低往高移动。 |
| 102 | + |
| 103 | +那么我们可以发现红线只有移动到 nums[i], nums[i] + k, nums[i] - k 时,才会突变。这个突变指的是可以通过操作使得频率变成多大的值会发生变化。也就是说,我们只需要考虑 nums[i], nums[i] + k, nums[i] - k 这三个值即可,而不是这之间的所有值。 |
| 104 | + |
| 105 | +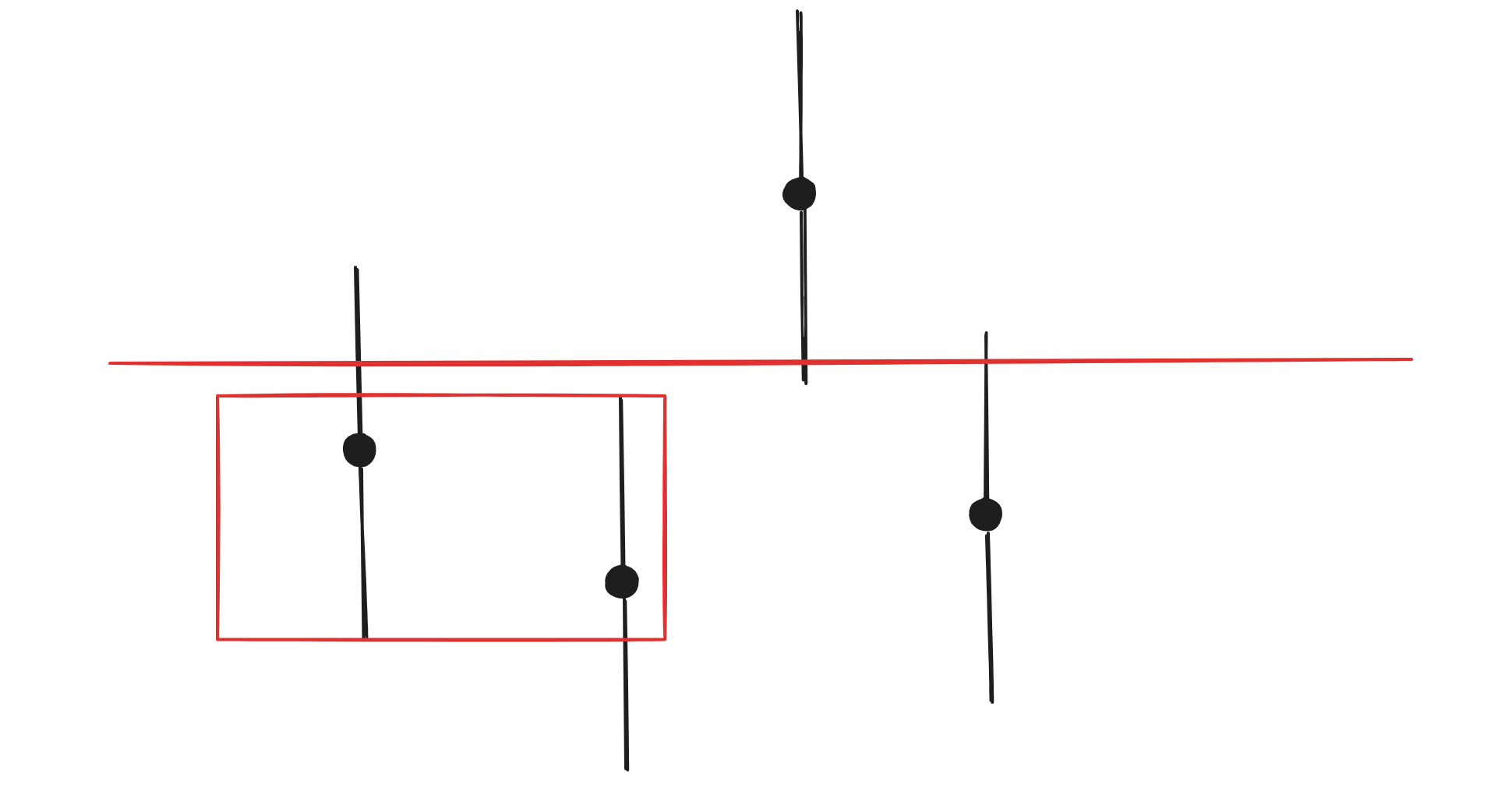 |
| 106 | + |
| 107 | +理解了上面的过程,最后只剩下一个问题。那就是对于每一个 v。找 满足 nums[i] - k <= v <= nums[i] + k 的有几个,我们就能操作几次,频率就能多多少(不考虑 numOperations 影响),当然要注意如果 v == nums[i] 就不需要操作。 |
| 108 | + |
| 109 | + |
| 110 | +具体来说: |
| 111 | + |
| 112 | +- 如果 nums[i] == v 不需要操作。 |
| 113 | +- 如果 nums[i] - k <= v <= nums[i] + k,操作一次 |
| 114 | +- 否则,无法操作 |
| 115 | + |
| 116 | +找 nums 中范围在某一个区间的个数如何做呢?我们可以使用二分查找。我们可以将 nums 排序,然后使用二分查找找到 nums 中第一个大于等于 v - k 的位置,和第一个大于 v + k 的位置,这两个位置之间的元素个数就是我们要找的。 |
| 117 | + |
| 118 | +最后一个小细节需要注意,能通过操作使得频率增加的量不能超过 numOperations。 |
| 119 | + |
| 120 | +## 关键点 |
| 121 | + |
| 122 | +- 枚举 nums 中的元素值 num 和 num + k, num - k 作为最高频率的元素的值 v |
| 123 | + |
| 124 | +## 代码 |
| 125 | + |
| 126 | +- 语言支持:Python3 |
| 127 | + |
| 128 | +Python3 Code: |
| 129 | + |
| 130 | +```python |
| 131 | +class Solution: |
| 132 | + def maxFrequency(self, nums: List[int], k: int, numOperations: int) -> int: |
| 133 | + # 把所有要考虑的值放进 set 里 |
| 134 | + st = set() |
| 135 | + # 统计 nums 里每种数出现了几次 |
| 136 | + mp = Counter(nums) |
| 137 | + for x in nums: |
| 138 | + st.add(x) |
| 139 | + st.add(x - k) |
| 140 | + st.add(x + k) |
| 141 | + |
| 142 | + # 给 nums 排序,方便接下来二分计数。 |
| 143 | + nums.sort() |
| 144 | + ans = 0 |
| 145 | + for x in st: |
| 146 | + except_self = ( |
| 147 | + bisect.bisect_right(nums, x + k) |
| 148 | + - bisect.bisect_left(nums, x - k) |
| 149 | + - mp[x] |
| 150 | + ) |
| 151 | + ans = max(ans, mp[x] + min(except_self, numOperations)) |
| 152 | + return ans |
| 153 | + |
| 154 | + |
| 155 | + |
| 156 | +``` |
| 157 | + |
| 158 | + |
| 159 | +**复杂度分析** |
| 160 | + |
| 161 | +令 n 为数组长度。 |
| 162 | + |
| 163 | +- 时间复杂度:$O(nlogn)$ |
| 164 | +- 空间复杂度:$O(n)$ |
| 165 | + |
| 166 | + |
| 167 | + |
| 168 | + |
| 169 | +> 此题解由 [力扣刷题插件](https://leetcode-pp.github.io/leetcode-cheat/?tab=solution-template) 自动生成。 |
| 170 | +
|
| 171 | +力扣的小伙伴可以[关注我](https://leetcode-cn.com/u/fe-lucifer/),这样就会第一时间收到我的动态啦~ |
| 172 | + |
| 173 | +以上就是本文的全部内容了。大家对此有何看法,欢迎给我留言,我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库:https://github.com/azl397985856/leetcode 。 目前已经 54K star 啦。大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。 |
| 174 | + |
| 175 | +关注公众号力扣加加,努力用清晰直白的语言还原解题思路,并且有大量图解,手把手教你识别套路,高效刷题。 |
| 176 | + |
| 177 | + |
0 commit comments