Skip to content

Latest commit

 

History

History
248 lines (193 loc) · 6.29 KB

821.shortest-distance-to-a-character.md

File metadata and controls

248 lines (193 loc) · 6.29 KB
Raw

题目地址(821. 字符的最短距离)

https://leetcode-cn.com/problems/shortest-distance-to-a-character

题目描述

给定一个字符串 S 和一个字符 C。返回一个代表字符串 S 中每个字符到字符串 S 中的字符 C 的最短距离的数组。

示例 1:

输入: S = "loveleetcode", C = 'e'
输出: [3, 2, 1, 0, 1, 0, 0, 1, 2, 2, 1, 0]
说明:

- 字符串 S 的长度范围为 [1, 10000]。
- C 是一个单字符，且保证是字符串 S 里的字符。
- S 和 C 中的所有字母均为小写字母。

前置知识

  • 数组的遍历(正向遍历和反向遍历)

思路

这道题就是让我们求的是向左或者向右距离目标字符最近的距离。

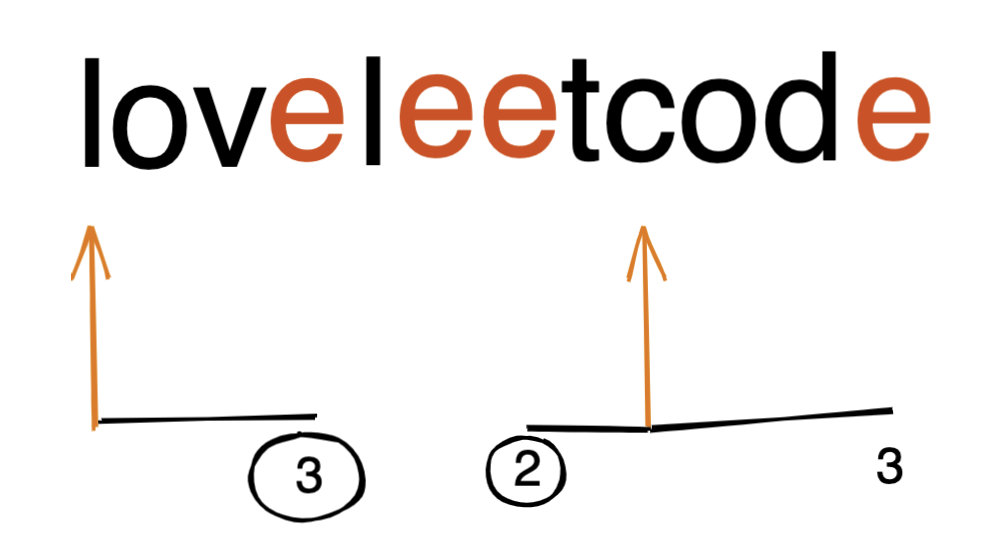
我画了个图方便大家理解：

比如我们要找第一个字符 l 的最近的字符 e，直观的想法就是向左向右分别搜索，遇到字符 e 就停止，比较两侧的距离，并取较小的即可。如上图，l 就是 3，c 就是 2。

这种直观的思路用代码来表示的话是这样的：

Python Code:

class Solution:
    def shortestToChar(self, S: str, C: str) -> List[int]:
        ans = []

        for i in range(len(S)):
            # 从 i 向左向右扩展
            l = r = i
            # 向左找到第一个 C
            while l > -1:
                if S[l] == C: break
                l -= 1
            # 向左找到第一个 C
            while r < len(S):
                if S[r] == C: break
                r += 1
            # 如果至死没有找到，则赋值一个无限大的数字，由于题目的数据范围是 [1, 10000]，因此 -10000 或者  10000就够了。
            if l == -1: l = -10000
            if r == len(S): r = 10000
            # 选较近的即可
            ans.append(min(r - i, i - l))
        return ans

复杂度分析

  • 时间复杂度：$O(N^2)$
  • 空间复杂度：$O(1)$

由于题目的数据范围是 $10^4$，因此通过所有的测试用例是没有问题的。

但是实际上，我们可以在线性的时间内解决。这里的关键点和上面的解法类似，也是两端遍历。不过不再是盲目的查找，因为这样做会有很多没有必要的计算。

我们可以使用空间换时间的方式来解，这里我使用类似单调栈的解法来解，大家也可以使用其他手段。关于单调栈的技巧，不在这里展开，感兴趣的可以期待我后面的专题。

class Solution:
    def shortestToChar(self, S: str, C: str) -> List[int]:
        ans = [10000] * len(S)
        stack = []
        for i in range(len(S)):
            while stack and S[i] == C:
                ans[stack.pop()] = i - stack[-1]
            if S[i] != C:stack.append(i)
            else: ans[i] = 0
        for i in range(len(S) - 1, -1, -1):
            while stack and S[i] == C:
                ans[stack.pop()] = min(ans[stack[-1]], stack[-1] - i)
            if S[i] != C:stack.append(i)
            else: ans[i] = 0

        return ans

复杂度分析

  • 时间复杂度：$O(N)$
  • 空间复杂度：$O(N)$

实际上，我们根本不需要栈来存储。原因很简单，那就是每次我们碰到目标字符 C 的时候， 我们就把栈全部清空了，因此我们用一个变量标识即可，具体参考后面的代码区。

如果碰到目标字符 C 的时候，不把栈清空，那么这个栈的空间多半是不能省的，反之可以省。

代码

代码支持：Python3，Java, CPP, Go, PHP

Python3 Code：

class Solution:
    def shortestToChar(self, S: str, C: str) -> List[int]:
        pre = -10000
        ans = []

        for i in range(len(S)):
            if S[i] == C: pre = i
            ans.append(i - pre)
        pre = 20000
        for i in range(len(S) - 1, -1, -1):
            if S[i] == C: pre = i
            ans[i] = min(ans[i], pre - i)
        return ans

Java Code：

class Solution {
    public int[] shortestToChar(String S, char C) {
        int N = S.length();
        int[] ans = new int[N];
        int prev = -10000;

        for (int i = 0; i < N; ++i) {
            if (S.charAt(i) == C) prev = i;
            ans[i] = i - prev;
        }

        prev = 20000;
        for (int i = N-1; i >= 0; --i) {
            if (S.charAt(i) == C) prev = i;
            ans[i] = Math.min(ans[i], prev - i);
        }

        return ans;
    }
}

CPP Code:

class Solution {
public:
   vector<int> shortestToChar(string S, char C) {
       vector<int> ans(S.size(), 0);
       int prev = -10000;
       for(int i = 0; i < S.size(); i ++){
           if(S[i] == C) prev = i;
           ans[i] = i - prev;
       }
       prev = 20000;
       for(int i = S.size() - 1; i >= 0; i --){
           if(S[i] == C) prev = i;
           ans[i] = min(ans[i], prev - i);
       }
       return ans;
   }
};

Go Code:

func shortestToChar(S string, C byte) []int {
    N := len(S)
    ans := make([]int, N)

    pre := -N // 最大距离
    for i := 0; i < N; i++ {
        if S[i] == C {
            pre = i
        }
        ans[i] = i - pre
    }

    pre = N*2 // 最大距离
    for i := N - 1; i >= 0; i-- {
        if S[i] == C {
            pre = i
        }
        ans[i] = min(ans[i], pre-i)
    }
    return ans
}

func min(a, b int) int {
    if a < b {
        return a
    }
    return b
}

PHP Code:

class Solution
{

    /**
     * @param String $S
     * @param String $C
     * @return Integer[]
     */
    function shortestToChar($S, $C)
    {
        $N = strlen($S);
        $ans = [];

        $pre = -$N;
        for ($i = 0; $i < $N; $i++) {
            if ($S[$i] == $C) {
                $pre = $i;
            }
            $ans[$i] = $i - $pre;
        }

        $pre = $N * 2;
        for ($i = $N - 1; $i >= 0; $i--) {
            if ($S[$i] == $C) {
                $pre = $i;
            }
            $ans[$i] = min($ans[$i], $pre - $i);
        }
        return $ans;
    }
}

复杂度分析

  • 时间复杂度：$O(N)$
  • 空间复杂度：$O(1)$

大家对此有何看法，欢迎给我留言，我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库：https://github.com/azl397985856/leetcode 。 目前已经 37K star 啦。

大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。