Document not found (404)
+This URL is invalid, sorry. Please use the navigation bar or search to continue.
+ +This URL is invalid, sorry. Please use the navigation bar or search to continue.
+ +++NOTE: This chapter is basically just an adaptation of F1/10ths chapter on the same subject (thanks creative commons!). +Please give their content a look for more info.
+
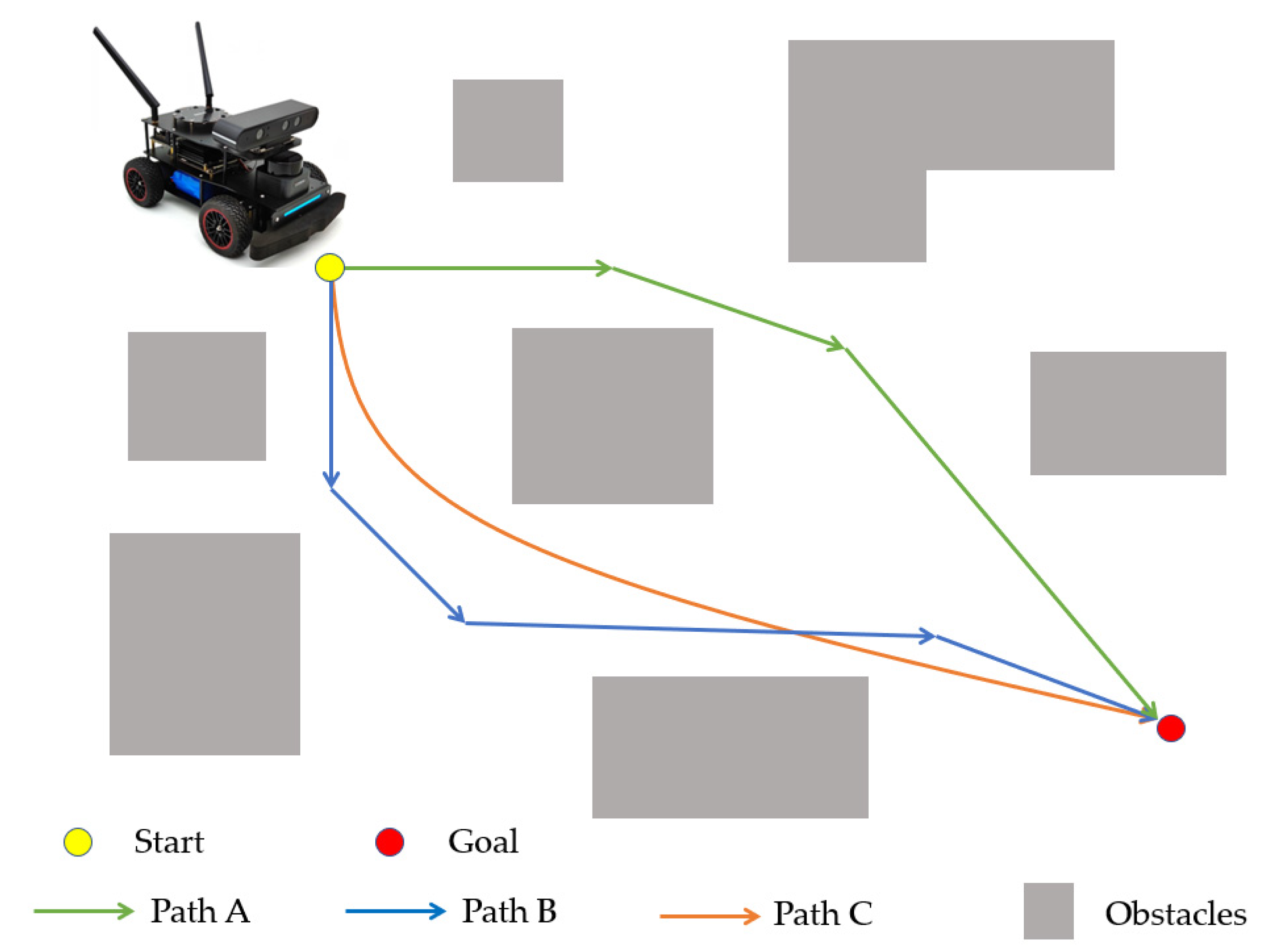
As mentioned before, the first part of our autonomous stack will be the planner, which determines the point we want to +send the kart to.
+As discussed prior, what a planner actually does depends on the goal of the robot. In the case of TinyKart, that would +be:
+Thus, a planner for TinyKart should aim to maximize these goals. The planners introduced in this chapter will not be the +best for this task, but show a possible approach.
+Considering these goals is important, as many existing approaches to planning (such as A*) don't make a ton of sense +in the context of TinyKart, and will lead to suboptimal results, even if they are completely acceptable in other +contexts.
+First off, we will introduce planners using F1/10ths follow the gap. This is an incredibly basic algorithm that decides +the next point to head to by simply finding the center point of the largest gap in each scan.
+ +
+Based off this description, the algorithm would look something like:
+scan[(start_idx+end_idex)/2]Of course, this is rather hand waving away item 2. What even is a gap? We can model one as a set of points from the scan +that fulfill two conditions:
+Thus, the algorithm now looks something like this:
+And as it turns out, that's really the best you can make the naive approach. The downfall of this approach is that it +has a tendency to cut corners, as the kart's limited turning radius means it needs to approach the corner from the far +wall in order to arc properly. The next approach we will discuss will aim to solve this.
+++NOTE: This section makes use of C++'s std::optional. If you haven't worked with it before, please check out this +article here.
+
While things are still simple, it's time for you to get your hands dirty and get this kart moving autonomously! In this +section, you will be implementing the above algorithm yourself. To begin, replace your main loop with the following:
+/// Finds a target point to drive to by finding the largest gap in the scan.
+///
+/// \param scan Lidar scan
+/// \param min_gap_size Minimum number of points in a gap required for it to be considered a gap
+/// \param min_dist Minimum distance for a point to be considered part of a gap, in m
+/// \return Target point to drive to, if a gap is found
+std::optional<ScanPoint> find_gap_naive(const std::vector<ScanPoint> &scan, uint8_t min_gap_size, float min_dist) {
+ // TODO
+}
+
+void loop() {
+ noInterrupts();
+ auto res = ld06.get_scan();
+ interrupts();
+
+ // Check if we have a scan frame
+ if (res) {
+ auto scan_res = *res;
+
+ // Check if frame erred
+ if (scan_res) {
+ auto maybe_scan = scan_builder.add_frame(scan_res.scan);
+
+ // Check if we have a 180 degree scan built
+ if (maybe_scan) {
+ auto scan = *maybe_scan;
+
+ auto front_obj_dist = scan[scan.size() / 2].dist(ScanPoint::zero());
+
+ // If object is 45cm in front of kart, stop (0.0 means bad point)
+ if (front_obj_dist != 0.0 && front_obj_dist < 0.45 + 0.1524) {
+ tinyKart->pause();
+ digitalWrite(LED_YELLOW, HIGH);
+ }
+
+ // Find target point TODO tune your params
+ auto maybe_target_pt = find_gap_naive(scan, 10, 2)
+
+ if (maybe_target_pt) {
+ auto target_pt = *maybe_target_pt;
+
+ logger.printf("Target point: (%hi,%hi)\n", (int16_t) (target_pt.x * 1000),
+ (int16_t) (target_pt.y * 1000));
+
+ // Find command to drive to point
+ auto command = pure_pursuit::calculate_command_to_point(tinyKart, target_pt, 1.0);
+
+ // Set throttle proportional to distance to point in front of kart
+ command.throttle_percent = mapfloat(front_obj_dist, 0.1, 10.0, 0.15, tinyKart->get_speed_cap());
+
+ logger.printf("Command: throttle %hu, angle %hi\n", (uint16_t) (command.throttle_percent * 100),
+ (int16_t) (command.steering_angle));
+
+ // Actuate kart
+ tinyKart->set_forward(command.throttle_percent);
+ tinyKart->set_steering(command.steering_angle);
+ }
+ }
+ } else {
+ switch (scan_res.error) {
+ case ScanResult::Error::CRCFail:
+ logger.printf("CRC error!\n");
+ break;
+
+ case ScanResult::Error::HeaderByteWrong:
+ logger.printf("Header byte wrong!\n");
+ break;
+ }
+ }
+ }
+}
+Don't worry about the loop much for now, as it contains the path tracker you will be making next chapter. A reference
+implementation is included here to ensure that you can test your planner. All you need to work on for now is find_gap_naive,
+which will contain the algorithm detailed above.
Once you have a complete implementation, test it with the tinykart in a relatively constrained space, so the lidar can +see things. Don't stress too much if it isn't perfect, but try to hack on the algorithm until you're confident you can't +make it better.
+This will likely take quite a long time, possibly days depending on how much time you have to work on TinyKart. Feel free +to take your time with this, and ensure you understand what is happening. This process will be very similar to when you're +working on it yourself, so its important to get this down.
+If you're ever completely stuck, there is a reference implementation in libs/gap_follow/naive_gap_follow.cpp.
+I would still try to finish this yourself though, because there are many ways to approach this implementation and things
+only get more complex from here.
With that experience under your belt, lets introduce another approach to the problem. This approach can be summarized as +"Throw yourself at the largest wall".
+ +
+Essentially, we redefine the largest gap to be the largest continues non-zero +span of points. This means that our target point will fling us directly at a wall. That's insane! Why would we want to +do that? The idea is that doing so will cause us to be on the outside of corners, which means that when we corner our +kart will have a wider angle to perform its turn. Done well, this almost looks like a racing line. Of course, with the +current implementation, we will just plow into a wall. So what stops us from doing so?
+To solve this issue, we add a "bubble" that removes points in front of the kart. This looks like:
+Because our gaps cannot contain zeroed points, this means that the kart cannot continue to head towards a wall, since +when it gets too close, those points are zeroed. This has the effect of the kart bouncing from the largest wall to the largest +wall, which has the desired cornering properties mentioned above.
+As it turns out, this bubble approach is actually very similar in implementation to the algorithm you just implemented. +It's main differences is the addition of the bubble, and the definition change of the gap. Otherwise, you are still +searching for the largest gap, and still need to scan the scan for gaps.
+Take your prior implementation, and adapt it to this new approach. You will need to modify both the function arguments +and body, but the rest of the code should still be fine.
+Once you've got this working, you're at feature parity with the reference kart! As before, a reference implementation of +this algorithm is in libs if you get stuck. Try to avoid using it though, as this will be great practice for working on +larger projects where I won't just hand you a template.
+Good luck!
+ +Ladies, gentleman, baby lidar - it's finally time to make TinyKart autonomous!
+This is going to be a multipart process, and be quite a bit more involved than the prior sections. This is why we're +doing this project after all.
+Before we look into algorithms, I want to give a very brief look at the way mobile robotics is 'normally' done. This +will +be very high level, but should you give you a decent mental model of what we've been doing this whole time.
+At a high level, autonomous stacks can be described using 'sense-think-act', a pretty ancient paradigm but one that +works for a simple system like TinyKart.
+For TinyKart, sense think act looks like the following:
+ +
+The idea of sense think act is that most robotics solutions form a pipeline where you read from sensors, plan based off +that new data, execute those plans, and finally repeat this over and over as the sensors get new data, and you progress +towards your goals.
+As you can see, you've actually already completed sense and act. All you need to do now is think, and wire it all +together!
+For mobile robotics, the think step above generally encompasses two main processes:
+Path planning is the act of taking the state of the world as input, and outputting a path for the robot to follow. +How this is done is entirely dependent on your sensors and goal for the robot.
+ +
+Generally speaking, a path is represented as a sequence of points to follow, rather than a line or something. For +TinyKart, we will actually only plan to a single point as we lack any sort of feedback on our speed, required to +use multipoint paths.
+Path planning algorithms span from general algorithms like A* or RRT to bespoke algorithms such as the gap +algorithms you will be writing.
+Path tracking algorithms take paths from a path planner and actually calculate the command the robot needs to perform to +follow the path.
+By command, we mean the value all actuators should be set to continue following the path. Because of this, path +trackers are independent of the path planner, but do depend on the actuators and geometry of your robot, known as +kinematics.
+For multipoint paths, this generally looks like:
+For our single point path, we only need to do step 2, which is considerably easier.
+For examples of path planning algorithms, see Pure Pursuit, DWB, and MPC.
+The following chapters will go more in depth on these two topics.
+ +++NOTE: This chapter makes significant use of resources from this article, +adapted for use in TinyKart. Please take a look there for more details on the math side of things.
+
Now that we have a target point, all you need to do is find out how to actually get the kart there. This is the +responsibility of path trackers.
+Much like path planners, path trackers come in many varieties, depending on the robot and requirements. For example, +some planners like Pure Pursuit simply directly head to the target, some like ROS's DWB attempt to avoid obstacles, +and some use advanced control algorithms such as Model Predictive Control to attempt to also handle vehicle dynamics +(such as wheel slip). These range in difficulty of implementation from elementary to reasurch.
+In the last chapter, you were using a reference implementation of pure pursuit. In this chapter, you will learn how to +reimplement this yourself, and get a better idea of how to tune it.
+Before we can talk about pure pursuit, we first need to introduce vehicle kinematics. Kinematics is the study of how +things move without respect to forces (dynamics). For example, the kinematics of a car define where the car will go +given some steering angle input alone, without considering things like wheel slip that depends on surface friction. +While far less accurate than using dynamics, robot kinematics gives us a good estimation of how our robot should move +given some command.
+Because kinematics doesn't depend on forces, it could be said that it instead relies on geometries. This means that +the physical layout of the robot defines your robot's kinematics. While these are theoretically infinite, they tend to +come in only a few varieties:
+Differential Drive:
+ +
+Skid Steer:
+ +
+Omnidirectional:
+ +
+And of course...
+Ackermann:
+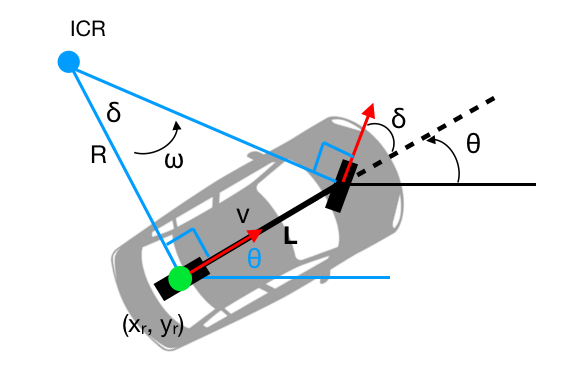 +
+Because cars use ackermann steering (as any other mechanism would fail at speed), we will only discuss ackermann +kinematics +in detail. Conveniently, the kart also uses ackermann steering so all of these equations apply to your real work.
+While one could model vehicle kinematics using all four wheels, it's common to simplify them down even further to just +two - the bicycle model:
+At this level of simplification, things should be pretty clear. To break it down:
+Some things to note:
+With that model in mind, we can now introduce pure pursuit. Pure pursuit is a path tracker that computes the command +to reach some target point by simply calculating the arc to that target point, and heading directly towards it. +With this in mind, it's clear why Ackermann kinematics are useful, as they give us a means to find a steering angle +given an arc.
+Pure pursuit is a tad more than that, however. It's main trinket is lookahead distance. Basically, PP will only +calculate arcs to points so far away from itself, in order to strike a balance between making sudden turns and slow +turns. You can think of lookahead distance as a tunable parameter that sets the "aggressiveness" of the karts steering.
+Let's go through a pure pursuit iteration step by step.
+When using a path with multiple points, the first step would be to find the intersection of the lookahead distance and +the path, in order to find the target point. For TinyKart we already have the target point, so this step isn't needed. +However, we still need to include the lookahead distance somehow, else pure pursuit will turn far too slowly.
+To do this, we simply do the following:
+To calculate the arc we need to follow to reach the target point (which remember, is given by R), we can exploit +the geometry of the problem.
+To find R, and thus the arc, we can use the law of sines in the geometry above to derive:
+\[ R = {distinceToTarget \over 2\sin(\alpha)} \]
+Finally, we need to calculate the steering angle required to take the arc described by R.
+By the bike model discussed prior, you can see that the steering angle relates to R by: +\[ \delta = \arctan({L \over{R}}) \]
+By substituting R for our arc found in the last step, we can solve the equation to find the required steering +angle \( \delta \).
+Now that we have our steering angle, which is our command, pure pursuit is complete.
+For a visual representation of pure pursuit in action, take a look at our pure pursuit implementation for Phoenix:
+ +Before I hand things off to you, I want to give a brief overview of tuning pure pursuit, since there isn't much media on +it.
+As mentioned before, lookahead is the main parameter for pure pursuit. For TinyKart, it directly controls the +aggressiveness +of a turn, since we drag target points closer to the kart, rather than sampling a closer point on a path. Because of +this, +a closer lookahead distance will always lead to a more aggressive turing angle, so long as the target point is farther +than the lookahead distance.
+Because of this, tuning lookahead on tinykart is rather simple, if tedious:
+Generally speaking, a larger lookahead distance should be faster, since turning causes the kart to lose speed from +friction.
+It's finally time for your last assignment! Of course, this will have you writing and tuning your own pure pursuit. +Build this off of your code from the last chapter.
+Find this line in your loop:
+auto command = pure_pursuit::calculate_command_to_point(tinyKart, target_pt, 1.0);
+And replace it with:
+auto command = calculate_command_to_point(tinyKart, target_pt, 1.0);
+Then somewhere in your main.cpp, add:
+/// Calculates the command to move the kart to some target point.
+AckermannCommand calculate_command_to_point(const TinyKart *tinyKart, ScanPoint target_point,
+ float max_lookahead) {
+ //TODO
+}
+Implement pure pursuit in this function, and test it our with your existing code.
+As a bit of an extra, consider using your past work from chapter 4 to set the throttle component of the command +proportionally to the distance to the objects in front of the kart.
+Good Luck!
+ +TODO cover what hardware is required, and explain its role
+ +Finally, lets set up the tinykart codebase now that everything else is installed.
+First, lets clone the tinykart codebase using Git. This will effectively copy code from GitHub and onto your local +machine.
+To do so:
+cd command to navigate to the directory you want to keep your code in. For
+example: cd C:\users\andy\documents\code\ on Windows or
+cd ~\Documents\code on *nix.git clone https://github.com/andyblarblar/tinykart-academyNext, lets flash the code onto the MCU, and actually see it running. To do this, we need to:
+First, open vscode. This should open to the example project from earlier. To change to tinykart, go to the file tab, and +select the "open folder" option, then open the tinykart folder:
+ +
+Make sure that you never connect power to both of the USB ports at the same time, as this will kill the board. +I have no idea why you would do this, but be warned.
+The STM board we use has an integrated ST-Link debugger, which we can connect to over USB to flash the controller, +debug, and more. To use this, connect a USB cable to the port on the side opposite to the Ethernet jack. If the port +on the other side is used, then the debugger will not be attached.
+You'll know the debugger is correctly connected when the MCU pops up like a USB drive. Make sure to mount this disk. +This is how PIO will know how to flash the controller.
+ +
+Finally, we can flash the code to the controller! This will involve compiling the code, creating the firmware file to +flash to the controller, and actually programming the controller with that firmware. Thankfully, PIO makes this process +trivial.
+To flash:
+ This button manages the controller we are targeting with this flash.
+
This button manages the controller we are targeting with this flash.
+If this process has succeeded, a few things will occur:
+To show that it's working, click the blue user button on the board. This will toggle the yellow LED:
+ +
+Congrats! You now have the tinykart software development environment setup. Before we dive in any further, I would +recommend poking around the codebase and messing with the code.
+ +TODO introduce the idea of the project, its goals, and audience
+ +Before we can do anything cool, we're going to have to get the development environment setup. This guide should work on +any operating system, but it will only be tested on Windows and Linux.
+ +Next, let's install Git, the ubiquitous version control system. If you're on Linux, this is likely already installed. +If you're on Windows, you likely don't.
+For Linux users, it's best to install Git using a package manager, such as through apt on debain:
+sudo apt install git
If you aren't on a debian based distro, then lets be honest, you don't need me to explain how to install Git.
+For Windows users, run the Git installer from the project's website.
+ +First, let's install PlatformIO, which will include our IDE and build system. While this can be done in a few ways, +we're going to be installing it via VScode, for sake of consistency. If you wish to use another IDE like CLion feel free +to do so at your own risk.
+To begin, navigate to the PIO website.
+You should see something like this:
+ +
+You're going to want to follow these steps, using the links on the site. Once you have the extension installed, I would +echo the guide in reccomending +the quick start +, which gives a very good overview of how to do the normal IDE motions.
+Once you've got everything ready, try to open PIO home by clicking the little house:
+ +
+This should open the home page:
+ +
+Click on the "New Project" button. This should bring up a modal to set up a new project. Name this project whatever, +and select "ST Nucleo H723ZG" as the board. Finally, keep Arduino as the framework, and finish the setup.
+After some time processing, the editor should now open to a new Arduino project. On the file explorer on the left,
+select src/main.cpp:
 +
+As you can see, the IDE has generated a same Arduino program, which should look quite familiar to anyone who has used +the +Arduino IDE before.
+As well, note the new icons on the bottom bar of the IDE, which represent various PIO commands (build, upload, etc):
+ +
+to make sure things are set up correctly, click the check mark shown above, which executes the build command. This +should +open a new terminal which displays the compilation. If successful, it should look like this:
+ +
+
+
+ TODO introduce the idea of the project, its goals, and audience
+ +Now that you have given TinyKart its proverbial eyes with the LiDAR, it's time to give it its proverbial legs (this +sounded better on paper lol). Specifically, we will be going over how to actually make the kart steer and accelerate. +Much like the LiDAR, you won't be writing all the driver code, but it's very important to understand how it all works, +since the patters appear all over embedded programming.
+Before we can program the hardware, we first need to discuss, well, the hardware! In robotics, anything that can make +a piece of a robot move is called an actuator. For example, the wheels on a Roomba, or the claw on Spot.
+The Traxxas Slash has two main means of actuation:
+Steering is achived with a servo motor:
+Servos are motors that are designed to hold a particular position, rather than continuing to rotate. By adding another +linkage, this rotational angle can be converted to a linear position, thus creating a linear actuator that can hold a +particular +distance. As it turns out, that's exactly how steering works! Essentially, mechanical linkages are geometrically +connected +to the servo such that each far end of the servos range will cause the wheels to reach their max turning angle.
+On the other hand, accelerating is something that requires a continues axis, so a servo would make no sense. In this +case, +the RC car simply uses a brushed DC motor:
+ +
+While discussion on brushed motors is better done by the more electrically inclined, a simple way to understand these +things +is that when you apply a voltage across the two leads, a magnetic field in the motor forms, moving the output shaft:
+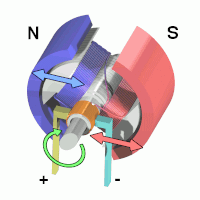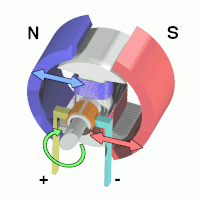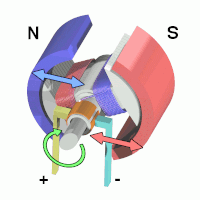 +
+Critically, the polarity of the voltage across the leads must switch, or else the motor will just stall. Thankfully, +there is dedicated hardware designed to do this for us, called a motor controller or ESC (Electronic Speed +Control). +The ESC on the Slash looks like this:
+ +
+The ESC sits between the battery and the motor, controlling the polarity and power as required to reach some level of +output speed. This means that when we want to move the motor, we need to interact with the ESC.
+So how to we actually control these actuators? Conveniently, they actually use the same exact interface. That is Pulse +Width Modulation (PWM).
+PWM shows up all over electrical things, both as an effectively analog power source, and as a digital signal, as it is +used here. +The idea of PWM is to represent an analog range like 0-100% using a digital signal, which can naturally only be 0 or 1. +While this could be done by sending binary integers, that would be extremely inefficient. Instead, PWM works by creating +set periods of time. Inside these periods, the percentage of time the signal is high versus low is the analog value +itself, +called the duty cycle. For a visualisation:
+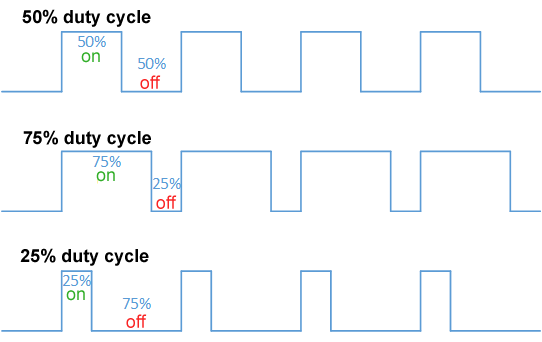 +
+The issue with this approach is that because the duty cycle is time on over period, the frequency of the PWM signal must +be set in stone. For historical reasons, RC cars do not like this, and use a different approch, called Pulse Period +Modulation.
+In this formulation, 0-100% is not the duty cycle, but rather a range of time the signal is high versus low. For +example, +most servos use 1.0ms high for min angle, 1.5ms high for their midpoint, and 2.0ms for their max angle. This approach +means +that any frequency with a period greater than 2.0ms can control the servo, allowing it to work with very cheap hardware.
+As it turns out, this is also exactly how the ESC works! The only difference being that 1.0ms is full reverse, and 2.0ms +is full forward power.
+Alright, now it's time for you to set up your controller to connect to these actuators. To do this, we're going to have +to do a tiny bit of wiring to get stuff setup. Each of the actuators has a connector like this:
+ +
+For the servo these pins mean:
+For the ESC these pins mean:
+Our goals for wiring things up is to:
+To do this:
+ +
+Red being A0, and green being D0.
+Now, connect the battery to the esc, and power to the controller. Now, press and hold the little blue +button on the ESC to turn it on. Finally, reset the controller. You should see the kart do a little jump, and +maybe move its wheels. This is good! This means that the ESC is armed, and ready to move.
+Now that things are hooked up, you can move the kart with commands on the TinyKart class:
+tinyKart->set_forward(command.throttle_percent);
+tinyKart->set_steering(command.steering_angle);
+Feel free to explore the other methods on the class, as they allow for movement in other ways, such as in reverse.
+While this high level API is all you will be working with for the autonomy, I want to briefly show how its implemented:
+ /// Sets the esc to power forward with some 0.0-1.0 percent.
+ void set_forward(float power) const {
+ assert(power <= 1.0 && power >= 0.0);
+
+ // Forward is 1.5-2.0ms periods
+ auto value = uint16_t(((1.5 + power * 0.5) / period) * max_pwm_duty);
+ analogWrite(pwm_pin, value);
+ }
+As you can see, its actually rather simple, thanks to Arduino. I want to untangle that second line for you, since +there's +really two things going on here.
+First, the value of that line is the value we are setting the hardware PWM peripheral's register to control the duty +cycle. Because PWM is digital, we can only output duty cycle percents up to some resolution in bits. Think of these as +buckets, +and the more buckets we have the more we can slice the 0-100% range into finer pieces to uniformly distribute among the +buckets. For example, Arduino defaults to an 8 bit PWM, which means that setting the register to 255 will be 100% duty +cycle, +0 will be 0%, and 255//2 will be closeish to 50%.
+In the case of our ST board, we have a 12-bit PWM, which means that we have 4092 "buckets". This means to select some +percent +duty cycle, you use the equation: \( power * 4092 \), where power is in range [0, 1].
+Second, the analogWrite call sets duty cycle, not duty width, which is what we're looking for. This means that we need
+to map our desired percent first from percent to width in ms, then from ms to duty cycle, then duty cycle to register
+value. This is exactly what that one-liner is doing. From left to right:
setup().analogWrite.The servo works exactly the same, except split over left vs right rather than reverse vs forwards.
+Now I said this is important to understand, even if you won't be writing it. Now's the time to ponder how this setup +could +influence the autonomy. Before you see the explanation, please think this over for a moment, to make sure you have a +good grasp on things.
+I would say this setup has two main consequences upstream in the autonomy stack:
+First, because PWM signals have a set period width, this limits the rate at which we can update the steering and speed, +since we must wait for the prior PWM period to end before we can change the duty cycle. While this isn't of massive +significance, +It's something to consider as adding, ex. 10ms of latency at 100Hz (what the reference code you have is using) is +actually +quite a large value on the embedded world.
+Second, 12-bits of resolution is quite high, but because we are stuck with only using small period ranges, we actually +have very little resolution. This means that while you can still get rather specific with your steering angles ( +certainly fine for our use), +small angle increments can sometimes have no effect or a large effect depending on if it causes us to step into +another "bucket".
+While neither of these are really something you need to worry about, its worth taking the time to think about how your +hardware will constrain your autonomous routines, as this is something that is far more pronounced on a full size +vehicle.
+Alright, now it's your turn to make the funny RC car move. Keep building off your last code, although you will need to +hack it a bit.
+Your challenge today is to make the kart slow proportionally to the distance in front of it. This will be very useful in +the autonomous routines later, as it will help prevent the kart from sliding around. Doing this will require you to use +distance values from the LiDAR again, but with it facing forward as is proper. Specifically, the kart should be able to +avoid hitting an object with much speed, and preferably stop before hitting it at all. Consider experimenting with +using reverse as a brake.
+Start slow and build your way up in speed and see how fast you can go! This experience will come in handy later when +testing autonomous things.
+Note that when the kart boots, it starts in a paused state, indicated by the yellow LED. In this state, it rejects all +commands. To allow it to move, press the blue button. Press the button again to stop the kart (this is what you were +doing the first day!). If you want to use this functionality in your own code (like to stop if the kart hit something):
+tinykart->pause(); // Stops
+tinykart->unpause(); // Starts
+Some notes before you start:
+To set the karts max speed, modify the 3rd parameter in the TinyKart constructor:
+ tinyKart = new TinyKart{STEERING_PIN, esc, 0.3, 4.5};
+It's finally time to play with our first piece of hardware!
+I would like to introduce the LD06, AKA Baby LiDAR!
+ +
+So why do we even have a LiDAR? Well, LiDARs provide a means to get a slice of the world around you as distance data. +This is extremely useful for mobile robots, since there really isn't another sensor that can give the same field of view +as a LiDAR.
+Generally speaking, there are two kinds of LiDAR, 2d and 3d. 3d LiDARs get distance values with both a vertical and +horizontal angle. 2d LiDARs, like the LD06, only get distance values from a flat plane. This makes them far less +versatile in the real world, but significantly easier to work with and cheaper.
+To get a mental model of how a LiDAR works, think of a laser rangefinder, such as those used in golf. You point it at +something, and it gives a distance reading at some frequency. Now think about what happens if we put that rangefinder +on a spinning motor. as the motor spins the rangefinder, the rangefinder will read a different location each time, +with a density of points proportional to is frequency. Given a high enough frequency, this readout will give you a +2d slice of the world around you as polar coordinates.
+For a visualization, take a look at this diagram from the LD06 user manual:
+ +
+Like all sensors, LiDAR has operating limits. For LiDARs, these limits are generally its frequency and range. +Unsurprisingly, +the LD06 is pretty bad at both, reading at 10Hz with a max range of 8-10m. This means that care needs to be taken to +avoid outpacing the speed of the LiDAR itself.
+The LD06 of course needs to connect to our board somehow. While industrial LiDARs generally use Ethernet for this +purpose, +our little baby lidar uses UART. UART, or RS232 (kinda, I'm not opening that debate) is a very simple protocol for +communication between embedded processors. While I won't get super into the weeds with how UART is implemented, think of +it as a very minimal layer over the idea of sending data over a wire as binary via high and low signals. In hardware, +UART is implemented (In most modern uses) as simply two or even just one wire, like so:
+ +
+UART is +an asynchronous protocol, that is, it does not have a clock line. This means that without prior configuration, the +receiver would have no way of knowing how fast the sender plans to send high and low bits. For UART, we call this +rate baud, measured in bits per second (effectively). This gives the advantage of removing the clock wire and thus +requiring less hardware, at the expense of anguish if you configure your reciver to a different baud than the sender.
+Also worth noting is that UART has no link-layer error detection, so higher layer protocols using UART almost always +include error detection methods such as Cyclical Redundancy Checks (CRCs) to ensure data integrity should there be +electrical noise in the system.
+Preamble aside, lets get the Baby connected. From the manual, the LD06 has the following pinout:
+ +
+As you can see, the LiDAR actually only has a UART transmitter, which means we will only need a UART receiver (Rx) on +the +board side. The PWM input is unused, and the other two pins are simply power and ground.
+While there are a variety of ways to connect these to the board, TinyKart is configured to use the following pins:
+ +
+Go ahead and connect these to the respective pins on the wire connected to baby lidar. The end result should look +something like this:
+ +
+With that being said, it's time to see the little guy come to life! Just plug in the board, and the LiDAR should spin to +life!
+ +
+First off, we need to figure out how to actually read the UART line connected to the LiDAR. This can be done in one of +two ways:
+Generally, polling is going to be slower but more convient, whereas interrupts require hardware support but allow for +hardware to communicate in parallel with your programs' execution.
+By default, Arduino essentially only allows for polling, as it uses the IRQ itself behind the scenes. This unfortunately +is actually too slow for how fast the LiDAR runs, so we have to make our own approach using interrupts. This is actually +quite complex and delves into STM HAL code, so the code won't be discussed here (if you're curious, check the dma.cpp +file).
+The LD06 sends its data in frames with the following format:
+ +
+As you can see, each frame from the lidar will be 47 bytes, and contain data between some start and end angle. Notice
+how
+all data is in large integer values. This is because sending floats over the wire is quite inefficient, so we simply
+scale
+up the values and use ints instead. The LSB and MSB refers to least and most significant bit respectively. This
+indicates
+the endiness of the data, or the ordering of each byte in multibyte structures. For example, if 0x270F(9999 decimal)
+is
+sent over this UART protocol, then it will actually be read and sent as 0x0F27. While this seems insane, this is
+actually
+how the ARM processor on the board already stores the ints. So by doing this, we can do simple C pointer magic to read
+the two bytes as a 16-bit integer:
packet.radar_speed = *reinterpret_cast<uint16_t *>(current_scan + 2);
+With all this layed out, our approach looks like the following:
+This approach is implemented in the ld06 driver provided for your use.
+Alright, that was quite the infodump. Let's take a look at the code you'll be working with, and actually see what this +looks like in action.
+Open main.cpp.
+On line 15 you'll see the creation of our driver:
+LD06 ld06{};
+Farther down in the setup, you'll see us configuring our callback to copy the buffer to the driver in the IRQ:
+ // Init DMA and UART for LiDAR
+ dmaSerialRx5.begin(230'400, [&](volatile LD06Buffer buffer) {
+ // On each packet received, copy over to driver.
+ ld06.add_buffer(buffer, 47);
+ });
+Finally, we poll the driver to see if a scan has been processed in the loop:
+ noInterrupts();
+ auto res = ld06.get_scan();
+ interrupts();
+Interrupts are disabled around the LiDAR to avoid issues when a new buffer arrives and starts copying right as we read +the previous buffer (known as a race condition).
+The processed scan frames have the following layout:
+struct LD06Frame {
+ /// The rotational speed of the unit, in degrees per second.
+ uint16_t radar_speed;
+ /// The starting angle of this scan, in degrees.
+ float start_angle;
+ /// Distance readings.
+ Range data[12];
+ /// The ending angle of this scan, in degrees.
+ float end_angle;
+ /// The timestamp of this scan, in ms. This will roll over at 30000.
+ uint16_t timestamp;
+ /// The CRC check from the lidar.
+ uint8_t crc8;
+Remember that each range is just a distance reading, which occurred at some angle. To retrieve this data, +we must interpolate the index with the start and end angles:
+ [[nodiscard]] float get_angle_of_reading(uint8_t reading_idx) const {
+ assert(reading_idx < 12);
+ auto angle = start_angle + get_step() * float(reading_idx);
+
+ if (angle > 360.0) {
+ angle -= 360.0;
+ }
+ return angle;
+ }
+With this, we have all that we need to interpret frames from the LiDAR! Armed with this information, +I recommend messing around with main.cpp to log data read by the board, and monitor the results by using the PIO +monitor.
+Cool, so we can read frames. As it turns out, this actually isn't all that useful. This is because each frame actually +only covers a very small region of the overall scan. This makes sending the LiDAR data much easier, but makes processing +on our end a bit more complicated. To remedy this, we must assemble scans by hand, as we receive frames. During this +process, +we can also do other forms of filtering on the frames to make the data easier to work with. This is generally called +scan preprocessing, +and is done on actual industrial robots.
+Our approach:
+This is implemented in the ScanBuilder class:
+ /// Adds a frame to the scan builder
+ std::optional<std::vector<ScanPoint>> add_frame(const LD06Frame &frame) {
+ // Filter to in range
+ if (scan_in_range(frame.start_angle, frame.end_angle)) {
+ last_scan_in_bounds = true;
+
+ // Convert points to cartiesian points
+ for (int i = 0; i < 12; ++i) {
+ // Skip points that are outside the scan, but some in the frame are
+ if (!scan_in_range(frame.get_angle_of_reading(i), frame.get_angle_of_reading(i))) continue;
+
+ auto [range, angle] = frame.get_range_in_polar(i);
+ float radian_angle = angle * (float(M_PI) / 180);
+
+ float x = range * sinf(radian_angle);
+ float y = -(range * cosf(radian_angle));
+
+ // Read noisy points as 0, which is what unreadable points are also received as
+ if (frame.data[i].confidence < 150) {
+ x = 0;
+ y = 0;
+ }
+
+ // Convert from mm to m
+ x /= 1000;
+ y /= 1000;
+
+ // Apply lidar offset
+ x += lidar_offset.x;
+ y += lidar_offset.y;
+
+ buffer.push_back(ScanPoint{x, y});
+ }
+ }
+ // Full scan area covered
+ else if (last_scan_in_bounds) {
+ last_scan_in_bounds = false;
+
+ return std::move(buffer);
+ }
+
+ return std::nullopt;
+ }
+In the tinykart default implementation, this is configured to read from -90 to 90 degrees:
+ScanBuilder scan_builder{360 - 90, 90, ScanPoint{0.1524, 0}};
+Time for you to get your hands dirty! Before anything else, replace your loop with the one below:
+void loop() {
+ noInterrupts();
+ auto res = ld06.get_scan();
+ interrupts();
+
+ // Check if we have a scan frame
+ if (res) {
+ auto scan_res = *res;
+
+ // Check if frame erred
+ if (scan_res) {
+ auto maybe_scan = scan_builder.add_frame(scan_res.scan);
+
+ // Check if we have a 180 degree scan built
+ if (maybe_scan) {
+ auto scan = *maybe_scan;
+
+ logger.printf("*****START SCAN******\n");
+ for (auto &pt: scan) {
+ logger.printf("Point: (%hu,%hu)\n", (uint16_t) pt.x, (uint16_t) pt.y);
+ }
+ logger.printf("*****END SCAN******\n\n");
+ }
+ } else {
+ switch (scan_res.error) {
+ case ScanResult::Error::CRCFail:
+ logger.printf("CRC error!\n");
+ break;
+
+ case ScanResult::Error::HeaderByteWrong:
+ logger.printf("Header byte wrong!\n");
+ break;
+ }
+ }
+ }
+}
+This code builds on the review section, and now also prints out completed scans, once they are built. Flash this to your +board, and open the PIO monitor. You should see data blaze by.
+Try putting our hand around the LiDAR. You should see the values lower. Something to note about these cartisian +coordinates +is that they are in right-hand-rule. That is, x is positive forwards and y is positive to the left. This is the standard +coordinate system in robotics.
+Now it's time for your challenge. Given the above code, create a program that prints "GOTCHA!" whenever someone +is 50cm or less from the back of the LiDAR. This will only require modifying things in main.cpp, and only in loop and +the globals. If you have any questions on units, formats etc., read the docs in the code! This is good practice for +working +on larger projects, since rarely will there be guides as verbose as this one to step through the code.
+Good luck!
+ +TODO cover the competition and some ideas
+ +TODO introduce the idea of the project, its goals, and audience
+TODO cover what hardware is required, and explain its role
+Before we can do anything cool, we're going to have to get the development environment setup. This guide should work on +any operating system, but it will only be tested on Windows and Linux.
+First, let's install PlatformIO, which will include our IDE and build system. While this can be done in a few ways, +we're going to be installing it via VScode, for sake of consistency. If you wish to use another IDE like CLion feel free +to do so at your own risk.
+To begin, navigate to the PIO website.
+You should see something like this:
+ +
+You're going to want to follow these steps, using the links on the site. Once you have the extension installed, I would +echo the guide in reccomending +the quick start +, which gives a very good overview of how to do the normal IDE motions.
+Once you've got everything ready, try to open PIO home by clicking the little house:
+ +
+This should open the home page:
+ +
+Click on the "New Project" button. This should bring up a modal to set up a new project. Name this project whatever, +and select "ST Nucleo H723ZG" as the board. Finally, keep Arduino as the framework, and finish the setup.
+After some time processing, the editor should now open to a new Arduino project. On the file explorer on the left,
+select src/main.cpp:
 +
+As you can see, the IDE has generated a same Arduino program, which should look quite familiar to anyone who has used +the +Arduino IDE before.
+As well, note the new icons on the bottom bar of the IDE, which represent various PIO commands (build, upload, etc):
+ +
+to make sure things are set up correctly, click the check mark shown above, which executes the build command. This +should +open a new terminal which displays the compilation. If successful, it should look like this:
+ +
+Next, let's install Git, the ubiquitous version control system. If you're on Linux, this is likely already installed. +If you're on Windows, you likely don't.
+For Linux users, it's best to install Git using a package manager, such as through apt on debain:
+sudo apt install git
If you aren't on a debian based distro, then lets be honest, you don't need me to explain how to install Git.
+For Windows users, run the Git installer from the project's website.
+Finally, lets set up the tinykart codebase now that everything else is installed.
+First, lets clone the tinykart codebase using Git. This will effectively copy code from GitHub and onto your local +machine.
+To do so:
+cd command to navigate to the directory you want to keep your code in. For
+example: cd C:\users\andy\documents\code\ on Windows or
+cd ~\Documents\code on *nix.git clone https://github.com/andyblarblar/tinykart-academyNext, lets flash the code onto the MCU, and actually see it running. To do this, we need to:
+First, open vscode. This should open to the example project from earlier. To change to tinykart, go to the file tab, and +select the "open folder" option, then open the tinykart folder:
+ +
+Make sure that you never connect power to both of the USB ports at the same time, as this will kill the board. +I have no idea why you would do this, but be warned.
+The STM board we use has an integrated ST-Link debugger, which we can connect to over USB to flash the controller, +debug, and more. To use this, connect a USB cable to the port on the side opposite to the Ethernet jack. If the port +on the other side is used, then the debugger will not be attached.
+You'll know the debugger is correctly connected when the MCU pops up like a USB drive. Make sure to mount this disk. +This is how PIO will know how to flash the controller.
+ +
+Finally, we can flash the code to the controller! This will involve compiling the code, creating the firmware file to +flash to the controller, and actually programming the controller with that firmware. Thankfully, PIO makes this process +trivial.
+To flash:
+ This button manages the controller we are targeting with this flash.
+
This button manages the controller we are targeting with this flash.
+If this process has succeeded, a few things will occur:
+To show that it's working, click the blue user button on the board. This will toggle the yellow LED:
+ +
+Congrats! You now have the tinykart software development environment setup. Before we dive in any further, I would +recommend poking around the codebase and messing with the code.
+Now that we have the codebase setup, let's briefly introduce what we're working with.
+Tinykart's embedded software is based on Arduino. If you somehow haven't heard of it, Arduino is an extremely high level +(as in simple) embedded programming framework. It's designed to allow for beginners and hobbyists to engage with +embedded +programming without spending a semester reading docs. If you've worked with Arduino before, you've probably worked with +the Arduino, the UNO v3:
+ +
+What most don't know is that Arduino is actually completely independent of the UNO, mega, and other "Arduino" branded +dev-boards. In this respect, Arduino is simply a C++ library, similar to something like ROS.
+So how does this work then? Well, Arduino can be ported between boards using what are called "Cores". Cores are
+basically
+just implementations of the Arduino API (think writeDigital(), readAnalog() etc.) using different, lower-level
+libraries specific to some board or vendor. This way, you can use Arduino the same way across boards, while the actual
+implementation is free to change (encapsulation, for those in SWE).
Because we are using the STM32H723GZ, we will be using STM32duino, +an +implementation of Arduino for STM32 MCU. This Arduino core is based on the STM32Cube HAL, something the more experienced +among you may have seen before. While not required, this does mean that we can actually use the STM HAL alongside +Arduino, +something that is used considerably behind the scenes, although you won't need to touch it.
+So what do we have available to us?
+PlatformIO is a build system and project configuration platform that works at a level above frameworks like Arduino or +the HAL. +While I won't get too far into the details here, PIO generally allows for embedded projects to be much more flexible by +allowing +the use of different tools like IDEs, while also providing a dependency manager similar to the Arduino IDE.
+One of the strongest features of PIO is its project structure, which allows for much more flexible projects than Arduino +IDE. This section will describe how to navigate this project structure.
+As of the time of writing, the tinykart repo looks like this:
+├── docs
+│ ├── io_setup.md
+│ ├── pinout.md
+│ ├── references.md
+│ └── refrence.pdf
+├── include
+│ ├── dma.hpp
+│ ├── logger.hpp
+│ ├── pins.hpp
+│ └── uart.hpp
+├── lib
+│ ├── gap_follow
+│ │ ├── common.hpp
+│ │ ├── f1tenth_gap_follow.cpp
+│ │ ├── f1tenth_gap_follow.hpp
+│ │ ├── naive_gap_follow.cpp
+│ │ └── naive_gap_follow.hpp
+│ ├── ld06
+│ │ ├── ld06.cpp
+│ │ └── ld06.hpp
+│ ├── pure_pursuit
+│ │ └── pure_pursuit.hpp
+│ ├── README
+│ └── tinykart
+│ ├── esc.hpp
+│ └── kart.hpp
+├── platformio.ini
+├── README.md
+├── src
+│ ├── dma.cpp
+│ ├── main.cpp
+│ └── stm32h7xx_hal_msp.c
+└── test
+ └── README
+To make things easier for you, we provide a bit of a framework for TinyKart, containing implementations of the harder +parts of using Arduino to interface with the required hardware. This section will contain a brief explanation of these +components.
+The TinyKart struct, implemented in the tinykart local lib, is an abstraction for working with the RC car hardware. It
+lives in global scope:
// Robot control
+TinyKart *tinyKart;
+You can use it to ex. move the steering to a certain angle, or set the throttle or brake:
+ // Actuate kart
+ tinyKart->set_forward(command.throttle_percent);
+ tinyKart->set_steering(command.steering_angle);
+The LD06 class is a driver for the LD06 Lidar. ScanBuilder is a class for working with the
+raw data returned from the driver. These both live in global scope:
LD06 ld06{};
+
+// Scan processor
+ScanBuilder scan_builder{360 - 90, 90, ScanPoint{0.1524, 0}};
+These will be introduced further in the next chapter.
+++NOTE: Because of newlib restrictions, attempting to print a floating point number will hardfault
+
Because we need to use the UART interrupt for the LiDAR driver, we are unable to use the Serial library. Because print
+debugging is quite useful, we reimplement a basic equivalent. The equivalent to Serial is now a global logger
+defined
+in logger.hpp.
Ex. to printf:
+
+ logger.printf("Target point: (%hi,%hi)\n", (int16_t) (target_pt.x * 1000),
+ (int16_t) (target_pt.y * 1000));
+
+Unlike the Serial library, this printf is actually non-blocking, and uses interrupts to process the message behind the +scenes. This means that there will be some lag before the message is printed, as it needs to be queued for +synchronisation +purposes.
+It's finally time to play with our first piece of hardware!
+I would like to introduce the LD06, AKA Baby LiDAR!
+ +
+So why do we even have a LiDAR? Well, LiDARs provide a means to get a slice of the world around you as distance data. +This is extremely useful for mobile robots, since there really isn't another sensor that can give the same field of view +as a LiDAR.
+Generally speaking, there are two kinds of LiDAR, 2d and 3d. 3d LiDARs get distance values with both a vertical and +horizontal angle. 2d LiDARs, like the LD06, only get distance values from a flat plane. This makes them far less +versatile in the real world, but significantly easier to work with and cheaper.
+To get a mental model of how a LiDAR works, think of a laser rangefinder, such as those used in golf. You point it at +something, and it gives a distance reading at some frequency. Now think about what happens if we put that rangefinder +on a spinning motor. as the motor spins the rangefinder, the rangefinder will read a different location each time, +with a density of points proportional to is frequency. Given a high enough frequency, this readout will give you a +2d slice of the world around you as polar coordinates.
+For a visualization, take a look at this diagram from the LD06 user manual:
+ +
+Like all sensors, LiDAR has operating limits. For LiDARs, these limits are generally its frequency and range. +Unsurprisingly, +the LD06 is pretty bad at both, reading at 10Hz with a max range of 8-10m. This means that care needs to be taken to +avoid outpacing the speed of the LiDAR itself.
+The LD06 of course needs to connect to our board somehow. While industrial LiDARs generally use Ethernet for this +purpose, +our little baby lidar uses UART. UART, or RS232 (kinda, I'm not opening that debate) is a very simple protocol for +communication between embedded processors. While I won't get super into the weeds with how UART is implemented, think of +it as a very minimal layer over the idea of sending data over a wire as binary via high and low signals. In hardware, +UART is implemented (In most modern uses) as simply two or even just one wire, like so:
+ +
+UART is +an asynchronous protocol, that is, it does not have a clock line. This means that without prior configuration, the +receiver would have no way of knowing how fast the sender plans to send high and low bits. For UART, we call this +rate baud, measured in bits per second (effectively). This gives the advantage of removing the clock wire and thus +requiring less hardware, at the expense of anguish if you configure your reciver to a different baud than the sender.
+Also worth noting is that UART has no link-layer error detection, so higher layer protocols using UART almost always +include error detection methods such as Cyclical Redundancy Checks (CRCs) to ensure data integrity should there be +electrical noise in the system.
+Preamble aside, lets get the Baby connected. From the manual, the LD06 has the following pinout:
+ +
+As you can see, the LiDAR actually only has a UART transmitter, which means we will only need a UART receiver (Rx) on +the +board side. The PWM input is unused, and the other two pins are simply power and ground.
+While there are a variety of ways to connect these to the board, TinyKart is configured to use the following pins:
+ +
+Go ahead and connect these to the respective pins on the wire connected to baby lidar. The end result should look +something like this:
+ +
+With that being said, it's time to see the little guy come to life! Just plug in the board, and the LiDAR should spin to +life!
+ +
+First off, we need to figure out how to actually read the UART line connected to the LiDAR. This can be done in one of +two ways:
+Generally, polling is going to be slower but more convient, whereas interrupts require hardware support but allow for +hardware to communicate in parallel with your programs' execution.
+By default, Arduino essentially only allows for polling, as it uses the IRQ itself behind the scenes. This unfortunately +is actually too slow for how fast the LiDAR runs, so we have to make our own approach using interrupts. This is actually +quite complex and delves into STM HAL code, so the code won't be discussed here (if you're curious, check the dma.cpp +file).
+The LD06 sends its data in frames with the following format:
+ +
+As you can see, each frame from the lidar will be 47 bytes, and contain data between some start and end angle. Notice
+how
+all data is in large integer values. This is because sending floats over the wire is quite inefficient, so we simply
+scale
+up the values and use ints instead. The LSB and MSB refers to least and most significant bit respectively. This
+indicates
+the endiness of the data, or the ordering of each byte in multibyte structures. For example, if 0x270F(9999 decimal)
+is
+sent over this UART protocol, then it will actually be read and sent as 0x0F27. While this seems insane, this is
+actually
+how the ARM processor on the board already stores the ints. So by doing this, we can do simple C pointer magic to read
+the two bytes as a 16-bit integer:
packet.radar_speed = *reinterpret_cast<uint16_t *>(current_scan + 2);
+With all this layed out, our approach looks like the following:
+This approach is implemented in the ld06 driver provided for your use.
+Alright, that was quite the infodump. Let's take a look at the code you'll be working with, and actually see what this +looks like in action.
+Open main.cpp.
+On line 15 you'll see the creation of our driver:
+LD06 ld06{};
+Farther down in the setup, you'll see us configuring our callback to copy the buffer to the driver in the IRQ:
+ // Init DMA and UART for LiDAR
+ dmaSerialRx5.begin(230'400, [&](volatile LD06Buffer buffer) {
+ // On each packet received, copy over to driver.
+ ld06.add_buffer(buffer, 47);
+ });
+Finally, we poll the driver to see if a scan has been processed in the loop:
+ noInterrupts();
+ auto res = ld06.get_scan();
+ interrupts();
+Interrupts are disabled around the LiDAR to avoid issues when a new buffer arrives and starts copying right as we read +the previous buffer (known as a race condition).
+The processed scan frames have the following layout:
+struct LD06Frame {
+ /// The rotational speed of the unit, in degrees per second.
+ uint16_t radar_speed;
+ /// The starting angle of this scan, in degrees.
+ float start_angle;
+ /// Distance readings.
+ Range data[12];
+ /// The ending angle of this scan, in degrees.
+ float end_angle;
+ /// The timestamp of this scan, in ms. This will roll over at 30000.
+ uint16_t timestamp;
+ /// The CRC check from the lidar.
+ uint8_t crc8;
+Remember that each range is just a distance reading, which occurred at some angle. To retrieve this data, +we must interpolate the index with the start and end angles:
+ [[nodiscard]] float get_angle_of_reading(uint8_t reading_idx) const {
+ assert(reading_idx < 12);
+ auto angle = start_angle + get_step() * float(reading_idx);
+
+ if (angle > 360.0) {
+ angle -= 360.0;
+ }
+ return angle;
+ }
+With this, we have all that we need to interpret frames from the LiDAR! Armed with this information, +I recommend messing around with main.cpp to log data read by the board, and monitor the results by using the PIO +monitor.
+Cool, so we can read frames. As it turns out, this actually isn't all that useful. This is because each frame actually +only covers a very small region of the overall scan. This makes sending the LiDAR data much easier, but makes processing +on our end a bit more complicated. To remedy this, we must assemble scans by hand, as we receive frames. During this +process, +we can also do other forms of filtering on the frames to make the data easier to work with. This is generally called +scan preprocessing, +and is done on actual industrial robots.
+Our approach:
+This is implemented in the ScanBuilder class:
+ /// Adds a frame to the scan builder
+ std::optional<std::vector<ScanPoint>> add_frame(const LD06Frame &frame) {
+ // Filter to in range
+ if (scan_in_range(frame.start_angle, frame.end_angle)) {
+ last_scan_in_bounds = true;
+
+ // Convert points to cartiesian points
+ for (int i = 0; i < 12; ++i) {
+ // Skip points that are outside the scan, but some in the frame are
+ if (!scan_in_range(frame.get_angle_of_reading(i), frame.get_angle_of_reading(i))) continue;
+
+ auto [range, angle] = frame.get_range_in_polar(i);
+ float radian_angle = angle * (float(M_PI) / 180);
+
+ float x = range * sinf(radian_angle);
+ float y = -(range * cosf(radian_angle));
+
+ // Read noisy points as 0, which is what unreadable points are also received as
+ if (frame.data[i].confidence < 150) {
+ x = 0;
+ y = 0;
+ }
+
+ // Convert from mm to m
+ x /= 1000;
+ y /= 1000;
+
+ // Apply lidar offset
+ x += lidar_offset.x;
+ y += lidar_offset.y;
+
+ buffer.push_back(ScanPoint{x, y});
+ }
+ }
+ // Full scan area covered
+ else if (last_scan_in_bounds) {
+ last_scan_in_bounds = false;
+
+ return std::move(buffer);
+ }
+
+ return std::nullopt;
+ }
+In the tinykart default implementation, this is configured to read from -90 to 90 degrees:
+ScanBuilder scan_builder{360 - 90, 90, ScanPoint{0.1524, 0}};
+Time for you to get your hands dirty! Before anything else, replace your loop with the one below:
+void loop() {
+ noInterrupts();
+ auto res = ld06.get_scan();
+ interrupts();
+
+ // Check if we have a scan frame
+ if (res) {
+ auto scan_res = *res;
+
+ // Check if frame erred
+ if (scan_res) {
+ auto maybe_scan = scan_builder.add_frame(scan_res.scan);
+
+ // Check if we have a 180 degree scan built
+ if (maybe_scan) {
+ auto scan = *maybe_scan;
+
+ logger.printf("*****START SCAN******\n");
+ for (auto &pt: scan) {
+ logger.printf("Point: (%hu,%hu)\n", (uint16_t) pt.x, (uint16_t) pt.y);
+ }
+ logger.printf("*****END SCAN******\n\n");
+ }
+ } else {
+ switch (scan_res.error) {
+ case ScanResult::Error::CRCFail:
+ logger.printf("CRC error!\n");
+ break;
+
+ case ScanResult::Error::HeaderByteWrong:
+ logger.printf("Header byte wrong!\n");
+ break;
+ }
+ }
+ }
+}
+This code builds on the review section, and now also prints out completed scans, once they are built. Flash this to your +board, and open the PIO monitor. You should see data blaze by.
+Try putting our hand around the LiDAR. You should see the values lower. Something to note about these cartisian +coordinates +is that they are in right-hand-rule. That is, x is positive forwards and y is positive to the left. This is the standard +coordinate system in robotics.
+Now it's time for your challenge. Given the above code, create a program that prints "GOTCHA!" whenever someone +is 50cm or less from the back of the LiDAR. This will only require modifying things in main.cpp, and only in loop and +the globals. If you have any questions on units, formats etc., read the docs in the code! This is good practice for +working +on larger projects, since rarely will there be guides as verbose as this one to step through the code.
+Good luck!
+Now that you have given TinyKart its proverbial eyes with the LiDAR, it's time to give it its proverbial legs (this +sounded better on paper lol). Specifically, we will be going over how to actually make the kart steer and accelerate. +Much like the LiDAR, you won't be writing all the driver code, but it's very important to understand how it all works, +since the patters appear all over embedded programming.
+Before we can program the hardware, we first need to discuss, well, the hardware! In robotics, anything that can make +a piece of a robot move is called an actuator. For example, the wheels on a Roomba, or the claw on Spot.
+The Traxxas Slash has two main means of actuation:
+Steering is achived with a servo motor:
+Servos are motors that are designed to hold a particular position, rather than continuing to rotate. By adding another +linkage, this rotational angle can be converted to a linear position, thus creating a linear actuator that can hold a +particular +distance. As it turns out, that's exactly how steering works! Essentially, mechanical linkages are geometrically +connected +to the servo such that each far end of the servos range will cause the wheels to reach their max turning angle.
+On the other hand, accelerating is something that requires a continues axis, so a servo would make no sense. In this +case, +the RC car simply uses a brushed DC motor:
+ +
+While discussion on brushed motors is better done by the more electrically inclined, a simple way to understand these +things +is that when you apply a voltage across the two leads, a magnetic field in the motor forms, moving the output shaft:
+ +
+Critically, the polarity of the voltage across the leads must switch, or else the motor will just stall. Thankfully, +there is dedicated hardware designed to do this for us, called a motor controller or ESC (Electronic Speed +Control). +The ESC on the Slash looks like this:
+ +
+The ESC sits between the battery and the motor, controlling the polarity and power as required to reach some level of +output speed. This means that when we want to move the motor, we need to interact with the ESC.
+So how to we actually control these actuators? Conveniently, they actually use the same exact interface. That is Pulse +Width Modulation (PWM).
+PWM shows up all over electrical things, both as an effectively analog power source, and as a digital signal, as it is +used here. +The idea of PWM is to represent an analog range like 0-100% using a digital signal, which can naturally only be 0 or 1. +While this could be done by sending binary integers, that would be extremely inefficient. Instead, PWM works by creating +set periods of time. Inside these periods, the percentage of time the signal is high versus low is the analog value +itself, +called the duty cycle. For a visualisation:
+ +
+The issue with this approach is that because the duty cycle is time on over period, the frequency of the PWM signal must +be set in stone. For historical reasons, RC cars do not like this, and use a different approch, called Pulse Period +Modulation.
+In this formulation, 0-100% is not the duty cycle, but rather a range of time the signal is high versus low. For +example, +most servos use 1.0ms high for min angle, 1.5ms high for their midpoint, and 2.0ms for their max angle. This approach +means +that any frequency with a period greater than 2.0ms can control the servo, allowing it to work with very cheap hardware.
+As it turns out, this is also exactly how the ESC works! The only difference being that 1.0ms is full reverse, and 2.0ms +is full forward power.
+Alright, now it's time for you to set up your controller to connect to these actuators. To do this, we're going to have +to do a tiny bit of wiring to get stuff setup. Each of the actuators has a connector like this:
+ +
+For the servo these pins mean:
+For the ESC these pins mean:
+Our goals for wiring things up is to:
+To do this:
+ +
+Red being A0, and green being D0.
+Now, connect the battery to the esc, and power to the controller. Now, press and hold the little blue +button on the ESC to turn it on. Finally, reset the controller. You should see the kart do a little jump, and +maybe move its wheels. This is good! This means that the ESC is armed, and ready to move.
+Now that things are hooked up, you can move the kart with commands on the TinyKart class:
+tinyKart->set_forward(command.throttle_percent);
+tinyKart->set_steering(command.steering_angle);
+Feel free to explore the other methods on the class, as they allow for movement in other ways, such as in reverse.
+While this high level API is all you will be working with for the autonomy, I want to briefly show how its implemented:
+ /// Sets the esc to power forward with some 0.0-1.0 percent.
+ void set_forward(float power) const {
+ assert(power <= 1.0 && power >= 0.0);
+
+ // Forward is 1.5-2.0ms periods
+ auto value = uint16_t(((1.5 + power * 0.5) / period) * max_pwm_duty);
+ analogWrite(pwm_pin, value);
+ }
+As you can see, its actually rather simple, thanks to Arduino. I want to untangle that second line for you, since +there's +really two things going on here.
+First, the value of that line is the value we are setting the hardware PWM peripheral's register to control the duty +cycle. Because PWM is digital, we can only output duty cycle percents up to some resolution in bits. Think of these as +buckets, +and the more buckets we have the more we can slice the 0-100% range into finer pieces to uniformly distribute among the +buckets. For example, Arduino defaults to an 8 bit PWM, which means that setting the register to 255 will be 100% duty +cycle, +0 will be 0%, and 255//2 will be closeish to 50%.
+In the case of our ST board, we have a 12-bit PWM, which means that we have 4092 "buckets". This means to select some +percent +duty cycle, you use the equation: \( power * 4092 \), where power is in range [0, 1].
+Second, the analogWrite call sets duty cycle, not duty width, which is what we're looking for. This means that we need
+to map our desired percent first from percent to width in ms, then from ms to duty cycle, then duty cycle to register
+value. This is exactly what that one-liner is doing. From left to right:
setup().analogWrite.The servo works exactly the same, except split over left vs right rather than reverse vs forwards.
+Now I said this is important to understand, even if you won't be writing it. Now's the time to ponder how this setup +could +influence the autonomy. Before you see the explanation, please think this over for a moment, to make sure you have a +good grasp on things.
+I would say this setup has two main consequences upstream in the autonomy stack:
+First, because PWM signals have a set period width, this limits the rate at which we can update the steering and speed, +since we must wait for the prior PWM period to end before we can change the duty cycle. While this isn't of massive +significance, +It's something to consider as adding, ex. 10ms of latency at 100Hz (what the reference code you have is using) is +actually +quite a large value on the embedded world.
+Second, 12-bits of resolution is quite high, but because we are stuck with only using small period ranges, we actually +have very little resolution. This means that while you can still get rather specific with your steering angles ( +certainly fine for our use), +small angle increments can sometimes have no effect or a large effect depending on if it causes us to step into +another "bucket".
+While neither of these are really something you need to worry about, its worth taking the time to think about how your +hardware will constrain your autonomous routines, as this is something that is far more pronounced on a full size +vehicle.
+Alright, now it's your turn to make the funny RC car move. Keep building off your last code, although you will need to +hack it a bit.
+Your challenge today is to make the kart slow proportionally to the distance in front of it. This will be very useful in +the autonomous routines later, as it will help prevent the kart from sliding around. Doing this will require you to use +distance values from the LiDAR again, but with it facing forward as is proper. Specifically, the kart should be able to +avoid hitting an object with much speed, and preferably stop before hitting it at all. Consider experimenting with +using reverse as a brake.
+Start slow and build your way up in speed and see how fast you can go! This experience will come in handy later when +testing autonomous things.
+Note that when the kart boots, it starts in a paused state, indicated by the yellow LED. In this state, it rejects all +commands. To allow it to move, press the blue button. Press the button again to stop the kart (this is what you were +doing the first day!). If you want to use this functionality in your own code (like to stop if the kart hit something):
+tinykart->pause(); // Stops
+tinykart->unpause(); // Starts
+Some notes before you start:
+To set the karts max speed, modify the 3rd parameter in the TinyKart constructor:
+ tinyKart = new TinyKart{STEERING_PIN, esc, 0.3, 4.5};
+Ladies, gentleman, baby lidar - it's finally time to make TinyKart autonomous!
+This is going to be a multipart process, and be quite a bit more involved than the prior sections. This is why we're +doing this project after all.
+Before we look into algorithms, I want to give a very brief look at the way mobile robotics is 'normally' done. This +will +be very high level, but should you give you a decent mental model of what we've been doing this whole time.
+At a high level, autonomous stacks can be described using 'sense-think-act', a pretty ancient paradigm but one that +works for a simple system like TinyKart.
+For TinyKart, sense think act looks like the following:
+ +
+The idea of sense think act is that most robotics solutions form a pipeline where you read from sensors, plan based off +that new data, execute those plans, and finally repeat this over and over as the sensors get new data, and you progress +towards your goals.
+As you can see, you've actually already completed sense and act. All you need to do now is think, and wire it all +together!
+For mobile robotics, the think step above generally encompasses two main processes:
+Path planning is the act of taking the state of the world as input, and outputting a path for the robot to follow. +How this is done is entirely dependent on your sensors and goal for the robot.
+ +
+Generally speaking, a path is represented as a sequence of points to follow, rather than a line or something. For +TinyKart, we will actually only plan to a single point as we lack any sort of feedback on our speed, required to +use multipoint paths.
+Path planning algorithms span from general algorithms like A* or RRT to bespoke algorithms such as the gap +algorithms you will be writing.
+Path tracking algorithms take paths from a path planner and actually calculate the command the robot needs to perform to +follow the path.
+By command, we mean the value all actuators should be set to continue following the path. Because of this, path +trackers are independent of the path planner, but do depend on the actuators and geometry of your robot, known as +kinematics.
+For multipoint paths, this generally looks like:
+For our single point path, we only need to do step 2, which is considerably easier.
+For examples of path planning algorithms, see Pure Pursuit, DWB, and MPC.
+The following chapters will go more in depth on these two topics.
+++NOTE: This chapter is basically just an adaptation of F1/10ths chapter on the same subject (thanks creative commons!). +Please give their content a look for more info.
+
As mentioned before, the first part of our autonomous stack will be the planner, which determines the point we want to +send the kart to.
+As discussed prior, what a planner actually does depends on the goal of the robot. In the case of TinyKart, that would +be:
+Thus, a planner for TinyKart should aim to maximize these goals. The planners introduced in this chapter will not be the +best for this task, but show a possible approach.
+Considering these goals is important, as many existing approaches to planning (such as A*) don't make a ton of sense +in the context of TinyKart, and will lead to suboptimal results, even if they are completely acceptable in other +contexts.
+First off, we will introduce planners using F1/10ths follow the gap. This is an incredibly basic algorithm that decides +the next point to head to by simply finding the center point of the largest gap in each scan.
+ +
+Based off this description, the algorithm would look something like:
+scan[(start_idx+end_idex)/2]Of course, this is rather hand waving away item 2. What even is a gap? We can model one as a set of points from the scan +that fulfill two conditions:
+Thus, the algorithm now looks something like this:
+And as it turns out, that's really the best you can make the naive approach. The downfall of this approach is that it +has a tendency to cut corners, as the kart's limited turning radius means it needs to approach the corner from the far +wall in order to arc properly. The next approach we will discuss will aim to solve this.
+++NOTE: This section makes use of C++'s std::optional. If you haven't worked with it before, please check out this +article here.
+
While things are still simple, it's time for you to get your hands dirty and get this kart moving autonomously! In this +section, you will be implementing the above algorithm yourself. To begin, replace your main loop with the following:
+/// Finds a target point to drive to by finding the largest gap in the scan.
+///
+/// \param scan Lidar scan
+/// \param min_gap_size Minimum number of points in a gap required for it to be considered a gap
+/// \param min_dist Minimum distance for a point to be considered part of a gap, in m
+/// \return Target point to drive to, if a gap is found
+std::optional<ScanPoint> find_gap_naive(const std::vector<ScanPoint> &scan, uint8_t min_gap_size, float min_dist) {
+ // TODO
+}
+
+void loop() {
+ noInterrupts();
+ auto res = ld06.get_scan();
+ interrupts();
+
+ // Check if we have a scan frame
+ if (res) {
+ auto scan_res = *res;
+
+ // Check if frame erred
+ if (scan_res) {
+ auto maybe_scan = scan_builder.add_frame(scan_res.scan);
+
+ // Check if we have a 180 degree scan built
+ if (maybe_scan) {
+ auto scan = *maybe_scan;
+
+ auto front_obj_dist = scan[scan.size() / 2].dist(ScanPoint::zero());
+
+ // If object is 45cm in front of kart, stop (0.0 means bad point)
+ if (front_obj_dist != 0.0 && front_obj_dist < 0.45 + 0.1524) {
+ tinyKart->pause();
+ digitalWrite(LED_YELLOW, HIGH);
+ }
+
+ // Find target point TODO tune your params
+ auto maybe_target_pt = find_gap_naive(scan, 10, 2)
+
+ if (maybe_target_pt) {
+ auto target_pt = *maybe_target_pt;
+
+ logger.printf("Target point: (%hi,%hi)\n", (int16_t) (target_pt.x * 1000),
+ (int16_t) (target_pt.y * 1000));
+
+ // Find command to drive to point
+ auto command = pure_pursuit::calculate_command_to_point(tinyKart, target_pt, 1.0);
+
+ // Set throttle proportional to distance to point in front of kart
+ command.throttle_percent = mapfloat(front_obj_dist, 0.1, 10.0, 0.15, tinyKart->get_speed_cap());
+
+ logger.printf("Command: throttle %hu, angle %hi\n", (uint16_t) (command.throttle_percent * 100),
+ (int16_t) (command.steering_angle));
+
+ // Actuate kart
+ tinyKart->set_forward(command.throttle_percent);
+ tinyKart->set_steering(command.steering_angle);
+ }
+ }
+ } else {
+ switch (scan_res.error) {
+ case ScanResult::Error::CRCFail:
+ logger.printf("CRC error!\n");
+ break;
+
+ case ScanResult::Error::HeaderByteWrong:
+ logger.printf("Header byte wrong!\n");
+ break;
+ }
+ }
+ }
+}
+Don't worry about the loop much for now, as it contains the path tracker you will be making next chapter. A reference
+implementation is included here to ensure that you can test your planner. All you need to work on for now is find_gap_naive,
+which will contain the algorithm detailed above.
Once you have a complete implementation, test it with the tinykart in a relatively constrained space, so the lidar can +see things. Don't stress too much if it isn't perfect, but try to hack on the algorithm until you're confident you can't +make it better.
+This will likely take quite a long time, possibly days depending on how much time you have to work on TinyKart. Feel free +to take your time with this, and ensure you understand what is happening. This process will be very similar to when you're +working on it yourself, so its important to get this down.
+If you're ever completely stuck, there is a reference implementation in libs/gap_follow/naive_gap_follow.cpp.
+I would still try to finish this yourself though, because there are many ways to approach this implementation and things
+only get more complex from here.
With that experience under your belt, lets introduce another approach to the problem. This approach can be summarized as +"Throw yourself at the largest wall".
+ +
+Essentially, we redefine the largest gap to be the largest continues non-zero +span of points. This means that our target point will fling us directly at a wall. That's insane! Why would we want to +do that? The idea is that doing so will cause us to be on the outside of corners, which means that when we corner our +kart will have a wider angle to perform its turn. Done well, this almost looks like a racing line. Of course, with the +current implementation, we will just plow into a wall. So what stops us from doing so?
+To solve this issue, we add a "bubble" that removes points in front of the kart. This looks like:
+Because our gaps cannot contain zeroed points, this means that the kart cannot continue to head towards a wall, since +when it gets too close, those points are zeroed. This has the effect of the kart bouncing from the largest wall to the largest +wall, which has the desired cornering properties mentioned above.
+As it turns out, this bubble approach is actually very similar in implementation to the algorithm you just implemented. +It's main differences is the addition of the bubble, and the definition change of the gap. Otherwise, you are still +searching for the largest gap, and still need to scan the scan for gaps.
+Take your prior implementation, and adapt it to this new approach. You will need to modify both the function arguments +and body, but the rest of the code should still be fine.
+Once you've got this working, you're at feature parity with the reference kart! As before, a reference implementation of +this algorithm is in libs if you get stuck. Try to avoid using it though, as this will be great practice for working on +larger projects where I won't just hand you a template.
+Good luck!
+++NOTE: This chapter makes significant use of resources from this article, +adapted for use in TinyKart. Please take a look there for more details on the math side of things.
+
Now that we have a target point, all you need to do is find out how to actually get the kart there. This is the +responsibility of path trackers.
+Much like path planners, path trackers come in many varieties, depending on the robot and requirements. For example, +some planners like Pure Pursuit simply directly head to the target, some like ROS's DWB attempt to avoid obstacles, +and some use advanced control algorithms such as Model Predictive Control to attempt to also handle vehicle dynamics +(such as wheel slip). These range in difficulty of implementation from elementary to reasurch.
+In the last chapter, you were using a reference implementation of pure pursuit. In this chapter, you will learn how to +reimplement this yourself, and get a better idea of how to tune it.
+Before we can talk about pure pursuit, we first need to introduce vehicle kinematics. Kinematics is the study of how +things move without respect to forces (dynamics). For example, the kinematics of a car define where the car will go +given some steering angle input alone, without considering things like wheel slip that depends on surface friction. +While far less accurate than using dynamics, robot kinematics gives us a good estimation of how our robot should move +given some command.
+Because kinematics doesn't depend on forces, it could be said that it instead relies on geometries. This means that +the physical layout of the robot defines your robot's kinematics. While these are theoretically infinite, they tend to +come in only a few varieties:
+Differential Drive:
+ +
+Skid Steer:
+ +
+Omnidirectional:
+ +
+And of course...
+Ackermann:
+ +
+Because cars use ackermann steering (as any other mechanism would fail at speed), we will only discuss ackermann +kinematics +in detail. Conveniently, the kart also uses ackermann steering so all of these equations apply to your real work.
+While one could model vehicle kinematics using all four wheels, it's common to simplify them down even further to just +two - the bicycle model:
+At this level of simplification, things should be pretty clear. To break it down:
+Some things to note:
+With that model in mind, we can now introduce pure pursuit. Pure pursuit is a path tracker that computes the command +to reach some target point by simply calculating the arc to that target point, and heading directly towards it. +With this in mind, it's clear why Ackermann kinematics are useful, as they give us a means to find a steering angle +given an arc.
+Pure pursuit is a tad more than that, however. It's main trinket is lookahead distance. Basically, PP will only +calculate arcs to points so far away from itself, in order to strike a balance between making sudden turns and slow +turns. You can think of lookahead distance as a tunable parameter that sets the "aggressiveness" of the karts steering.
+Let's go through a pure pursuit iteration step by step.
+When using a path with multiple points, the first step would be to find the intersection of the lookahead distance and +the path, in order to find the target point. For TinyKart we already have the target point, so this step isn't needed. +However, we still need to include the lookahead distance somehow, else pure pursuit will turn far too slowly.
+To do this, we simply do the following:
+To calculate the arc we need to follow to reach the target point (which remember, is given by R), we can exploit +the geometry of the problem.
+To find R, and thus the arc, we can use the law of sines in the geometry above to derive:
+\[ R = {distinceToTarget \over 2\sin(\alpha)} \]
+Finally, we need to calculate the steering angle required to take the arc described by R.
+By the bike model discussed prior, you can see that the steering angle relates to R by: +\[ \delta = \arctan({L \over{R}}) \]
+By substituting R for our arc found in the last step, we can solve the equation to find the required steering +angle \( \delta \).
+Now that we have our steering angle, which is our command, pure pursuit is complete.
+For a visual representation of pure pursuit in action, take a look at our pure pursuit implementation for Phoenix:
+ +Before I hand things off to you, I want to give a brief overview of tuning pure pursuit, since there isn't much media on +it.
+As mentioned before, lookahead is the main parameter for pure pursuit. For TinyKart, it directly controls the +aggressiveness +of a turn, since we drag target points closer to the kart, rather than sampling a closer point on a path. Because of +this, +a closer lookahead distance will always lead to a more aggressive turing angle, so long as the target point is farther +than the lookahead distance.
+Because of this, tuning lookahead on tinykart is rather simple, if tedious:
+Generally speaking, a larger lookahead distance should be faster, since turning causes the kart to lose speed from +friction.
+It's finally time for your last assignment! Of course, this will have you writing and tuning your own pure pursuit. +Build this off of your code from the last chapter.
+Find this line in your loop:
+auto command = pure_pursuit::calculate_command_to_point(tinyKart, target_pt, 1.0);
+And replace it with:
+auto command = calculate_command_to_point(tinyKart, target_pt, 1.0);
+Then somewhere in your main.cpp, add:
+/// Calculates the command to move the kart to some target point.
+AckermannCommand calculate_command_to_point(const TinyKart *tinyKart, ScanPoint target_point,
+ float max_lookahead) {
+ //TODO
+}
+Implement pure pursuit in this function, and test it our with your existing code.
+As a bit of an extra, consider using your past work from chapter 4 to set the throttle component of the command +proportionally to the distance to the objects in front of the kart.
+Good Luck!
+TODO cover the competition and some ideas
+ +Now that we have the codebase setup, let's briefly introduce what we're working with.
+Tinykart's embedded software is based on Arduino. If you somehow haven't heard of it, Arduino is an extremely high level +(as in simple) embedded programming framework. It's designed to allow for beginners and hobbyists to engage with +embedded +programming without spending a semester reading docs. If you've worked with Arduino before, you've probably worked with +the Arduino, the UNO v3:
+ +
+What most don't know is that Arduino is actually completely independent of the UNO, mega, and other "Arduino" branded +dev-boards. In this respect, Arduino is simply a C++ library, similar to something like ROS.
+So how does this work then? Well, Arduino can be ported between boards using what are called "Cores". Cores are
+basically
+just implementations of the Arduino API (think writeDigital(), readAnalog() etc.) using different, lower-level
+libraries specific to some board or vendor. This way, you can use Arduino the same way across boards, while the actual
+implementation is free to change (encapsulation, for those in SWE).
Because we are using the STM32H723GZ, we will be using STM32duino, +an +implementation of Arduino for STM32 MCU. This Arduino core is based on the STM32Cube HAL, something the more experienced +among you may have seen before. While not required, this does mean that we can actually use the STM HAL alongside +Arduino, +something that is used considerably behind the scenes, although you won't need to touch it.
+So what do we have available to us?
+PlatformIO is a build system and project configuration platform that works at a level above frameworks like Arduino or +the HAL. +While I won't get too far into the details here, PIO generally allows for embedded projects to be much more flexible by +allowing +the use of different tools like IDEs, while also providing a dependency manager similar to the Arduino IDE.
+One of the strongest features of PIO is its project structure, which allows for much more flexible projects than Arduino +IDE. This section will describe how to navigate this project structure.
+As of the time of writing, the tinykart repo looks like this:
+├── docs
+│ ├── io_setup.md
+│ ├── pinout.md
+│ ├── references.md
+│ └── refrence.pdf
+├── include
+│ ├── dma.hpp
+│ ├── logger.hpp
+│ ├── pins.hpp
+│ └── uart.hpp
+├── lib
+│ ├── gap_follow
+│ │ ├── common.hpp
+│ │ ├── f1tenth_gap_follow.cpp
+│ │ ├── f1tenth_gap_follow.hpp
+│ │ ├── naive_gap_follow.cpp
+│ │ └── naive_gap_follow.hpp
+│ ├── ld06
+│ │ ├── ld06.cpp
+│ │ └── ld06.hpp
+│ ├── pure_pursuit
+│ │ └── pure_pursuit.hpp
+│ ├── README
+│ └── tinykart
+│ ├── esc.hpp
+│ └── kart.hpp
+├── platformio.ini
+├── README.md
+├── src
+│ ├── dma.cpp
+│ ├── main.cpp
+│ └── stm32h7xx_hal_msp.c
+└── test
+ └── README
+To make things easier for you, we provide a bit of a framework for TinyKart, containing implementations of the harder +parts of using Arduino to interface with the required hardware. This section will contain a brief explanation of these +components.
+The TinyKart struct, implemented in the tinykart local lib, is an abstraction for working with the RC car hardware. It
+lives in global scope:
// Robot control
+TinyKart *tinyKart;
+You can use it to ex. move the steering to a certain angle, or set the throttle or brake:
+ // Actuate kart
+ tinyKart->set_forward(command.throttle_percent);
+ tinyKart->set_steering(command.steering_angle);
+The LD06 class is a driver for the LD06 Lidar. ScanBuilder is a class for working with the
+raw data returned from the driver. These both live in global scope:
LD06 ld06{};
+
+// Scan processor
+ScanBuilder scan_builder{360 - 90, 90, ScanPoint{0.1524, 0}};
+These will be introduced further in the next chapter.
+++NOTE: Because of newlib restrictions, attempting to print a floating point number will hardfault
+
Because we need to use the UART interrupt for the LiDAR driver, we are unable to use the Serial library. Because print
+debugging is quite useful, we reimplement a basic equivalent. The equivalent to Serial is now a global logger
+defined
+in logger.hpp.
Ex. to printf:
+
+ logger.printf("Target point: (%hi,%hi)\n", (int16_t) (target_pt.x * 1000),
+ (int16_t) (target_pt.y * 1000));
+
+Unlike the Serial library, this printf is actually non-blocking, and uses interrupts to process the message behind the +scenes. This means that there will be some lag before the message is printed, as it needs to be queued for +synchronisation +purposes.
+ +