给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例 1:
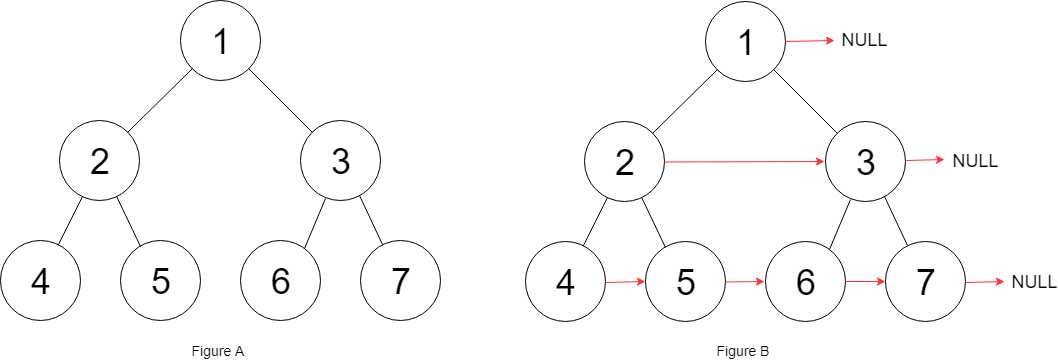
输入:root = [1,2,3,4,5,6,7] 输出:[1,#,2,3,#,4,5,6,7,#] 解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束。
示例 2:
输入:root = [] 输出:[]
提示:
- 树中节点的数量在
[0, 212 - 1]范围内 -1000 <= node.val <= 1000
进阶:
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
“BFS 层次遍历”实现。
"""
# Definition for a Node.
class Node:
def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
self.val = val
self.left = left
self.right = right
self.next = next
"""
class Solution:
def connect(self, root: 'Node') -> 'Node':
if root is None or (root.left is None and root.right is None):
return root
q = deque([root])
while q:
size = len(q)
cur = None
for _ in range(size):
node = q.popleft()
if node.right:
q.append(node.right)
if node.left:
q.append(node.left)
node.next = cur
cur = node
return root/*
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node next;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, Node _left, Node _right, Node _next) {
val = _val;
left = _left;
right = _right;
next = _next;
}
};
*/
class Solution {
public Node connect(Node root) {
if (root == null || (root.left == null && root.right == null)) {
return root;
}
Deque<Node> q = new ArrayDeque<>();
q.offer(root);
while (!q.isEmpty()) {
Node cur = null;
for (int i = 0, n = q.size(); i < n; ++i) {
Node node = q.pollFirst();
if (node.right != null) {
q.offer(node.right);
}
if (node.left != null) {
q.offer(node.left);
}
node.next = cur;
cur = node;
}
}
return root;
}
}/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node* next;
Node() : val(0), left(NULL), right(NULL), next(NULL) {}
Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
Node(int _val, Node* _left, Node* _right, Node* _next)
: val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
Node* connect(Node* root) {
if (!root || (!root->left && !root->right)) {
return root;
}
queue<Node*> q;
q.push(root);
while (!q.empty()) {
Node* cur = nullptr;
for (int i = 0, n = q.size(); i < n; ++i) {
Node* node = q.front();
q.pop();
if (node->right) {
q.push(node->right);
}
if (node->left) {
q.push(node->left);
}
node->next = cur;
cur = node;
}
}
return root;
}
};/**
* Definition for Node.
* class Node {
* val: number
* left: Node | null
* right: Node | null
* next: Node | null
* constructor(val?: number, left?: Node, right?: Node, next?: Node) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* this.next = (next===undefined ? null : next)
* }
* }
*/
function connect(root: Node | null): Node | null {
if (root == null) {
return root;
}
const { left, right } = root;
if (left != null) {
left.next = right;
}
if (right != null && root.next != null) {
root.right.next = root.next.left;
}
connect(root.left);
connect(root.right);
return root;
}