README.md

2508. 添加边使所有节点度数都为偶数

English Version

题目描述

给你一个有 n 个节点的 无向 图，节点编号为 1 到 n 。再给你整数 n 和一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条边。图不一定连通。

你可以给图中添加 至多 两条额外的边（也可以一条边都不添加），使得图中没有重边也没有自环。

如果添加额外的边后，可以使得图中所有点的度数都是偶数，返回 true ，否则返回 false 。

点的度数是连接一个点的边的数目。

 

示例 1：

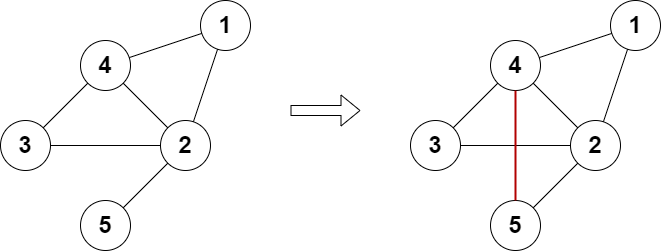
输入：n = 5, edges = [[1,2],[2,3],[3,4],[4,2],[1,4],[2,5]]
输出：true
解释：上图展示了添加一条边的合法方案。
最终图中每个节点都连接偶数条边。

示例 2：

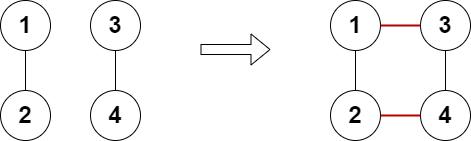
输入：n = 4, edges = [[1,2],[3,4]]
输出：true
解释：上图展示了添加两条边的合法方案。

示例 3：

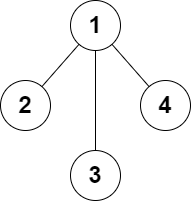
输入：n = 4, edges = [[1,2],[1,3],[1,4]]
输出：false
解释：无法添加至多 2 条边得到一个符合要求的图。

 

提示：

• 3 <= n <= 105
• 2 <= edges.length <= 105
• edges[i].length == 2
• 1 <= ai, bi <= n
• ai != bi
• 图中不会有重边

解法

方法一：分类讨论

我们先通过 edges 构建图 $g$，然后找出所有度数为奇数的点，记为 $vs$。

如果 $vs$ 的长度为 $0$，说明图 $g$ 中所有点的度数都是偶数，直接返回 true 即可。

如果 $vs$ 的长度为 $2$，说明图 $g$ 中有两个点的度数是奇数。如果我们可以直接用一条边连接这两个点，使得图 $g$ 中所有点的度数都是偶数，返回 true；否则，如果我们能找到第三个点 $c$，使得我们能够连接 $a$ 和 $c$，以及连接 $b$ 和 $c$，使得图 $g$ 中所有点的度数都是偶数，返回 true；否则，返回 false。

如果 $vs$ 的长度为 $4$，我们枚举两两组合的所有情况，判断是否存在满足条件的情况，是则返回 true；否则，返回 false。

其它情况，返回 false。

时间复杂度 $O(n + m)$，空间复杂度 $O(n + m)$。其中 $n$ 和 $m$ 分别为节点的数量和边的数量。

Python3

class Solution:
    def isPossible(self, n: int, edges: List[List[int]]) -> bool:
        g = defaultdict(set)
        for a, b in edges:
            g[a].add(b)
            g[b].add(a)
        vs = [i for i, v in g.items() if len(v) & 1]
        if len(vs) == 0:
            return True
        if len(vs) == 2:
            a, b = vs
            if a not in g[b]:
                return True
            return any(a not in g[c] and c not in g[b] for c in range(1, n + 1))
        if len(vs) == 4:
            a, b, c, d = vs
            if a not in g[b] and c not in g[d]:
                return True
            if a not in g[c] and b not in g[d]:
                return True
            if a not in g[d] and b not in g[c]:
                return True
            return False
        return False

Java

class Solution {
    public boolean isPossible(int n, List<List<Integer>> edges) {
        Set<Integer>[] g = new Set[n + 1];
        Arrays.setAll(g, k -> new HashSet<>());
        for (var e : edges) {
            int a = e.get(0), b = e.get(1);
            g[a].add(b);
            g[b].add(a);
        }
        List<Integer> vs = new ArrayList<>();
        for (int i = 1; i <= n; ++i) {
            if (g[i].size() % 2 == 1) {
                vs.add(i);
            }
        }
        if (vs.size() == 0) {
            return true;
        }
        if (vs.size() == 2) {
            int a = vs.get(0), b = vs.get(1);
            if (!g[a].contains(b)) {
                return true;
            }
            for (int c = 1; c <= n; ++c) {
                if (a != c && b != c && !g[a].contains(c) && !g[c].contains(b)) {
                    return true;
                }
            }
            return false;
        }
        if (vs.size() == 4) {
            int a = vs.get(0), b = vs.get(1), c = vs.get(2), d = vs.get(3);
            if (!g[a].contains(b) && !g[c].contains(d)) {
                return true;
            }
            if (!g[a].contains(c) && !g[b].contains(d)) {
                return true;
            }
            if (!g[a].contains(d) && !g[b].contains(c)) {
                return true;
            }
            return false;
        }
        return false;
    }
}

C++

class Solution {
public:
    bool isPossible(int n, vector<vector<int>>& edges) {
        vector<unordered_set<int>> g(n + 1);
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].insert(b);
            g[b].insert(a);
        }
        vector<int> vs;
        for (int i = 1; i <= n; ++i) {
            if (g[i].size() % 2) {
                vs.emplace_back(i);
            }
        }
        if (vs.size() == 0) {
            return true;
        }
        if (vs.size() == 2) {
            int a = vs[0], b = vs[1];
            if (!g[a].count(b)) return true;
            for (int c = 1; c <= n; ++c) {
                if (a != b && b != c && !g[a].count(c) && !g[c].count(b)) {
                    return true;
                }
            }
            return false;
        }
        if (vs.size() == 4) {
            int a = vs[0], b = vs[1], c = vs[2], d = vs[3];
            if (!g[a].count(b) && !g[c].count(d)) return true;
            if (!g[a].count(c) && !g[b].count(d)) return true;
            if (!g[a].count(d) && !g[b].count(c)) return true;
            return false;
        }
        return false;
    }
};

Go

func isPossible(n int, edges [][]int) bool {
	g := make([]map[int]bool, n+1)
	for _, e := range edges {
		a, b := e[0], e[1]
		if g[a] == nil {
			g[a] = map[int]bool{}
		}
		if g[b] == nil {
			g[b] = map[int]bool{}
		}
		g[a][b], g[b][a] = true, true
	}
	vs := []int{}
	for i := 1; i <= n; i++ {
		if len(g[i])%2 == 1 {
			vs = append(vs, i)
		}
	}
	if len(vs) == 0 {
		return true
	}
	if len(vs) == 2 {
		a, b := vs[0], vs[1]
		if !g[a][b] {
			return true
		}
		for c := 1; c <= n; c++ {
			if a != c && b != c && !g[a][c] && !g[c][b] {
				return true
			}
		}
		return false
	}
	if len(vs) == 4 {
		a, b, c, d := vs[0], vs[1], vs[2], vs[3]
		if !g[a][b] && !g[c][d] {
			return true
		}
		if !g[a][c] && !g[b][d] {
			return true
		}
		if !g[a][d] && !g[b][c] {
			return true
		}
		return false
	}
	return false
}

...