Skip to content

Latest commit

 

History

History
193 lines (158 loc) · 5.89 KB

README.md

File metadata and controls

193 lines (158 loc) · 5.89 KB
Raw

2077. 殊途同归

English Version

题目描述

迷宫由 n 个从 1 到 n 的房间组成，有些房间由走廊连接。给定一个二维整数数组 corridors，其中 corridors[i] = [room1i, room2i] 表示有一条走廊连接 room1i 和room2i，允许迷宫中的一个人从 room1i 到 room1i ，反之亦然。

迷宫的设计者想知道迷宫有多让人困惑。迷宫的 混乱分数 是 长度为 3 的不同的环的数量。

  • 例如, 1 → 2 → 3 → 1 是长度为 3 的环, 但 1 → 2 → 3 → 4 和 1 → 2 → 3 → 2 → 1 不是。

如果在第一个环中访问的一个或多个房间 不在 第二个环中，则认为两个环是 不同 的。

返回迷宫的混乱分数。

示例 1:

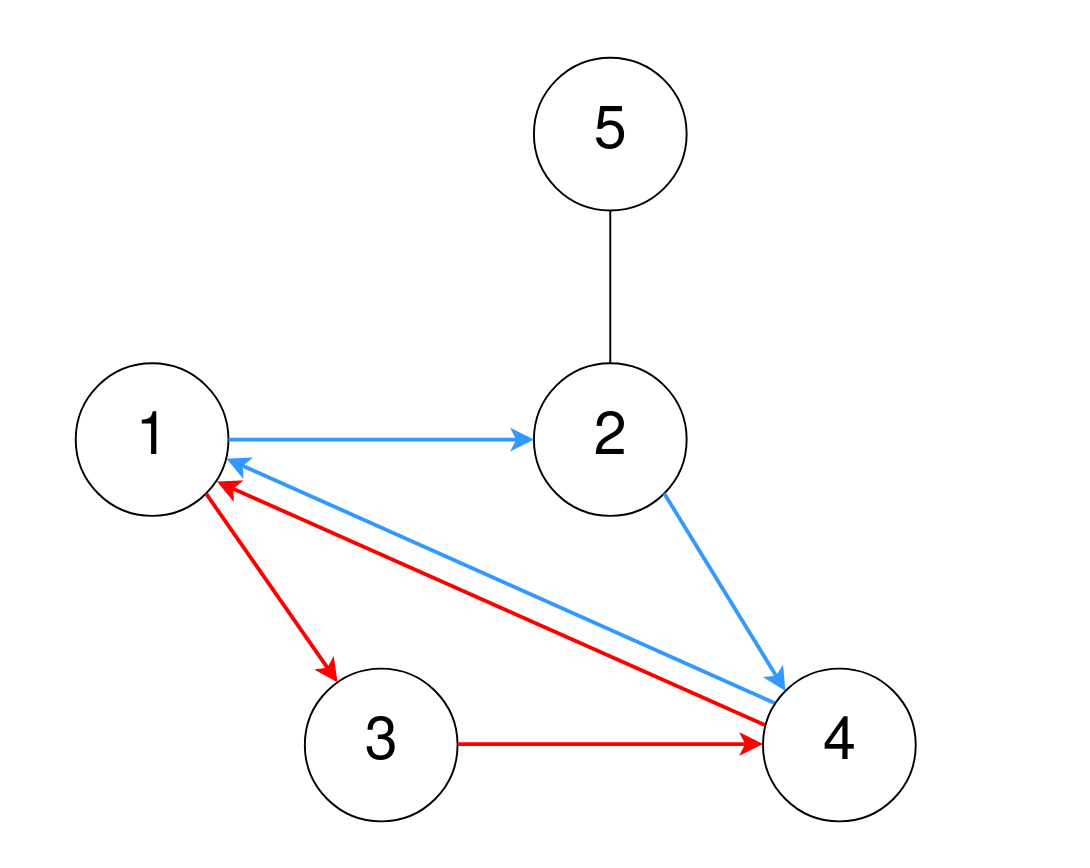
输入: n = 5, corridors = [[1,2],[5,2],[4,1],[2,4],[3,1],[3,4]]
输出: 2
解释:
一个长度为 3 的环为 4→1→3→4，用红色表示。
注意，这是与 3→4→1→3 或 1→3→4→1 相同的环，因为房间是相同的。
另一个长度为 3 的环为 1→2→4→1，用蓝色表示。
因此，有两个长度为 3 的不同的环。

示例 2:

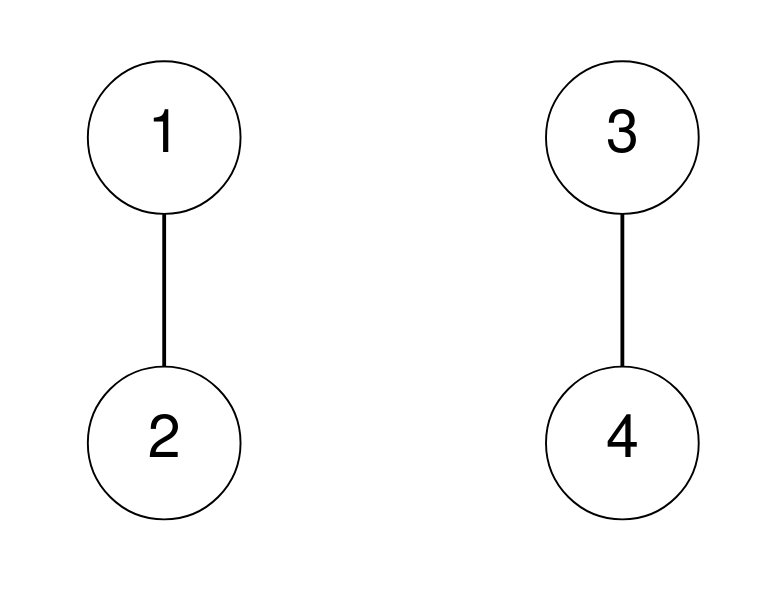
输入: n = 4, corridors = [[1,2],[3,4]]
输出: 0
解释:
没有长度为 3 的环。

 

提示:

  • 2 <= n <= 1000
  • 1 <= corridors.length <= 5 * 104
  • corridors[i].length == 2
  • 1 <= room1i, room2i <= n
  • room1i != room2i

  • 没有重复的走廊。

解法

方法一：哈希表

长度为 3 的环，由三个顶点、三条边组成。我们假设三个顶点分别为 a, b, c。

那么一定存在 c <=> a，c <=> b 以及 a <=> b，即环中的每个点都与其他两点直接相连。我们可以用哈希表来存放每个点的相邻点。

由于环的长度为 3，每个相同的环会被重复统计 3 次，因此答案需除以 3。

时间复杂度 $O(n^2)$，空间复杂度 $O(n)$。

Python3

class Solution:
    def numberOfPaths(self, n: int, corridors: List[List[int]]) -> int:
        g = defaultdict(set)
        for a, b in corridors:
            g[a].add(b)
            g[b].add(a)
        ans = 0
        for i in range(1, n + 1):
            for j, k in combinations(g[i], 2):
                if j in g[k]:
                    ans += 1
        return ans // 3

Java

class Solution {
    public int numberOfPaths(int n, int[][] corridors) {
        Set<Integer>[] g = new Set[n + 1];
        for (int i = 0; i <= n; ++i) {
            g[i] = new HashSet<>();
        }
        for (var c : corridors) {
            int a = c[0], b = c[1];
            g[a].add(b);
            g[b].add(a);
        }
        int ans = 0;
        for (int c = 1; c <= n; ++c) {
            var nxt = new ArrayList<>(g[c]);
            int m = nxt.size();
            for (int i = 0; i < m; ++i) {
                for (int j = i + 1; j < m; ++j) {
                    int a = nxt.get(i), b = nxt.get(j);
                    if (g[b].contains(a)) {
                        ++ans;
                    }
                }
            }
        }
        return ans / 3;
    }
}

C++

class Solution {
public:
    int numberOfPaths(int n, vector<vector<int>>& corridors) {
        vector<unordered_set<int>> g(n + 1);
        for (auto& c : corridors) {
            int a = c[0], b = c[1];
            g[a].insert(b);
            g[b].insert(a);
        }
        int ans = 0;
        for (int c = 1; c <= n; ++c) {
            vector<int> nxt;
            nxt.assign(g[c].begin(), g[c].end());
            int m = nxt.size();
            for (int i = 0; i < m; ++i) {
                for (int j = i + 1; j < m; ++j) {
                    int a = nxt[i], b = nxt[j];
                    ans += g[b].count(a);
                }
            }
        }
        return ans / 3;
    }
};

Go

func numberOfPaths(n int, corridors [][]int) int {
	g := make([]map[int]bool, n+1)
	for i := range g {
		g[i] = make(map[int]bool)
	}
	for _, c := range corridors {
		a, b := c[0], c[1]
		g[a][b] = true
		g[b][a] = true
	}
	ans := 0
	for c := 1; c <= n; c++ {
		nxt := []int{}
		for v := range g[c] {
			nxt = append(nxt, v)
		}
		m := len(nxt)
		for i := 0; i < m; i++ {
			for j := i + 1; j < m; j++ {
				a, b := nxt[i], nxt[j]
				if g[b][a] {
					ans++
				}
			}
		}
	}
	return ans / 3
}

...