Skip to content

Latest commit

 

History

History
160 lines (116 loc) · 6 KB

README.md

File metadata and controls

160 lines (116 loc) · 6 KB
Raw

2065. 最大化一张图中的路径价值

English Version

题目描述

给你一张 无向 图，图中有 n 个节点，节点编号从 0 到 n - 1 （都包括）。同时给你一个下标从 0 开始的整数数组 values ，其中 values[i] 是第 i 个节点的 价值 。同时给你一个下标从 0 开始的二维整数数组 edges ，其中 edges[j] = [uj, vj, timej] 表示节点 uj 和 vj 之间有一条需要 timej 秒才能通过的无向边。最后，给你一个整数 maxTime 。

合法路径 指的是图中任意一条从节点 0 开始，最终回到节点 0 ，且花费的总时间 不超过 maxTime 秒的一条路径。你可以访问一个节点任意次。一条合法路径的 价值 定义为路径中 不同节点 的价值 之和 （每个节点的价值 至多 算入价值总和中一次）。

请你返回一条合法路径的 最大 价值。

注意：每个节点 至多 有 四条 边与之相连。

 

示例 1：

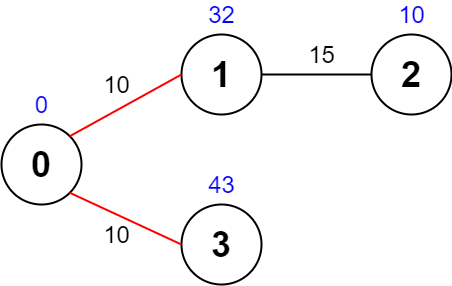
输入：values = [0,32,10,43], edges = [[0,1,10],[1,2,15],[0,3,10]], maxTime = 49
输出：75
解释：
一条可能的路径为：0 -> 1 -> 0 -> 3 -> 0 。总花费时间为 10 + 10 + 10 + 10 = 40 <= 49 。
访问过的节点为 0 ，1 和 3 ，最大路径价值为 0 + 32 + 43 = 75 。

示例 2：

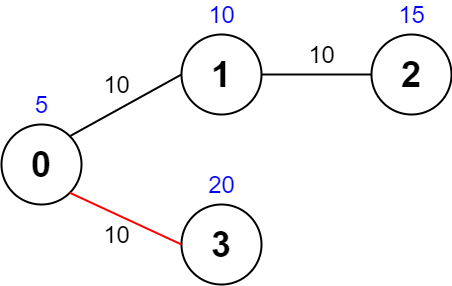
输入：values = [5,10,15,20], edges = [[0,1,10],[1,2,10],[0,3,10]], maxTime = 30
输出：25
解释：
一条可能的路径为：0 -> 3 -> 0 。总花费时间为 10 + 10 = 20 <= 30 。
访问过的节点为 0 和 3 ，最大路径价值为 5 + 20 = 25 。

示例 3：

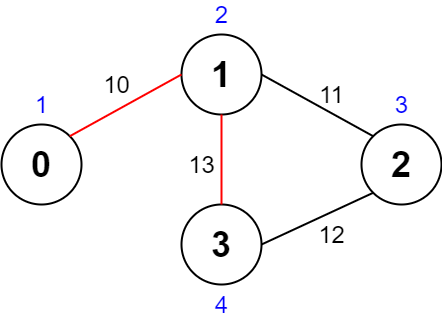
输入：values = [1,2,3,4], edges = [[0,1,10],[1,2,11],[2,3,12],[1,3,13]], maxTime = 50
输出：7
解释：
一条可能的路径为：0 -> 1 -> 3 -> 1 -> 0 。总花费时间为 10 + 13 + 13 + 10 = 46 <= 50 。
访问过的节点为 0 ，1 和 3 ，最大路径价值为 1 + 2 + 4 = 7 。

示例 4：

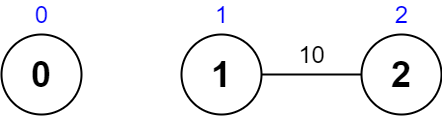
输入：values = [0,1,2], edges = [[1,2,10]], maxTime = 10
输出：0
解释：
唯一一条路径为 0 。总花费时间为 0 。
唯一访问过的节点为 0 ，最大路径价值为 0 。

 

提示：

  • n == values.length
  • 1 <= n <= 1000
  • 0 <= values[i] <= 108
  • 0 <= edges.length <= 2000
  • edges[j].length == 3
  • 0 <= uj < vj <= n - 1
  • 10 <= timej, maxTime <= 100
  • [uj, vj] 所有节点对 互不相同 。
  • 每个节点 至多有四条 边。
  • 图可能不连通。

解法

DFS

Python3



Java





TypeScript


function maximalPathQuality(
    values: number[],
    edges: number[][],
    maxTime: number,
): number {
    const n = values.length;
    let g: Array<Array<Array<number>>> = Array.from(
        { length: n },
        v => new Array(),
    );
    for (let edge of edges) {
        let [u, v, t] = edge;
        g[u].push([v, t]);
        g[v].push([u, t]);
    }
    let visited = new Array(n).fill(false);
    let ans = 0;

    function dfs(u: number, time: number, value: number): void {
        // 索引0为终点
        if (!u) {
            ans = Math.max(value, ans);
        }
        for (let [v, dist] of g[u]) {
            if (time - dist >= 0) {
                if (!visited[v]) {
                    visited[v] = true;
                    dfs(v, time - dist, value + values[v]);
                    visited[v] = false; // 回溯
                } else {
                    dfs(v, time - dist, value);
                }
            }
        }
    }

    // 索引0为起点
    visited[0] = true;
    dfs(0, maxTime, values[0]);

    return ans;
}


...