README.md

1902. 给定二叉搜索树的插入顺序求深度

English Version

题目描述

给定一个从 0 开始索引的整数类型数组 order ，其长度为 n，是从 1 到 n 的所有整数的一个排列，表示插入到一棵二叉搜索树的顺序。

二叉搜索树的定义如下：

• 一个节点的左子树只包含键值小于该节点键值的节点。
• 一个节点的右子树只包含键值大于该节点键值的节点。
• 左子树和右子树须均为二叉搜索树。

该二叉搜索树的构造方式如下：

• order[0] 将成为该二叉搜索树的根。
• 所有后续的元素均在维持二叉搜索树性质的前提下作为任何已存在节点的子节点插入。

返回该二叉搜索树的深度。

一棵二叉树的深度是从根节点到最远叶节点的最长路径所经节点的个数。

 

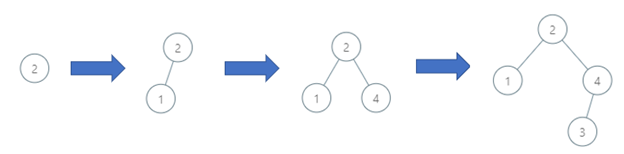
示例 1:

输入: order = [2,1,4,3]
输出: 3
解释: 该二叉搜索树的深度为 3，路径为 2->4->3。

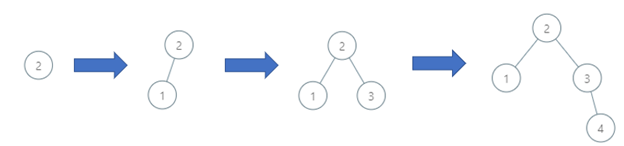
示例 2:

输入: order = [2,1,3,4]
输出: 3
解释: 该二叉搜索树的深度为 3，路径为 2->3->4。

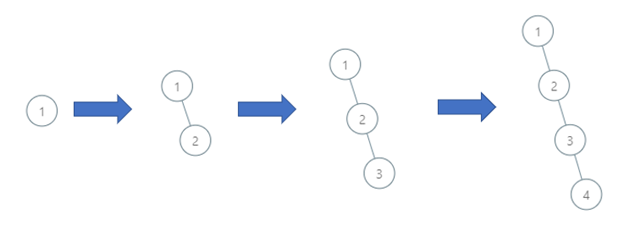
示例 3:

输入: order = [1,2,3,4]
输出: 4
解释: 该二叉搜索树的深度为 4，路径为 1->2->3->4。

 

提示：

• n == order.length
• 1 <= n <= 105
• order 是从 1 到 n 的整数的一个排列。

解法

从二叉搜索树的原理出发，任意一个新节点加入到二叉搜索树，都是从 root 节点开始，如果比当前节点小，就往左子树遍历，如果比当前节点大，就往右子树遍历。所以，新节点的最终父节点，一定是在原树中，并且是绝对值之差最接近的两个元素之一。

这样我们就可以通过二分查找，从原二叉搜索树中，来确定 lower,higher 边界节点。

确定左右节点边界之后怎么办呢？很简单，只要找 lower 和 higher 中 深度较大的那个节点即可。

为什么呢？因为在原树中，有 root 的存在，lower 和 higher，只会在 root 的同一侧子树中，不会跨过 root 节点。

可以用反证法证明，如果 lower 和 higher 分别在 root 的左子树和右子树中，那么一定存在 lower < root < higher 的情况，对于 newNode 也位于 (lower,higher) 的开区间中，又 newNode.val ≠ root.val ，则区间情况会变为 (lower,root) 或者 (root,higher)，与之前产生了矛盾。所以，lower 和 higher 只会在 root 的同一侧子树中。

那么，对于 lower 和 higher 来说，只存在两种情况：

1. lower 在 higher 的左子树中
2. higher 在 lower 的右子树中

对于情况 1，则表示 higher 存在一个左孩子节点（至少左子树中存在一个 lower 节点），所以，新节点不能成为到 higher 的左孩子，那么新节点只能成为 lower 的右孩子，而 lower 在 higher 的左子树中，则 lower.depth > higher.depth。

情况 2 同理可证。

Python3

from sortedcontainers import SortedDict


class Solution:
    def maxDepthBST(self, order: List[int]) -> int:
        sd = SortedDict({0: 0, inf: 0, order[0]: 1})
        ans = 1
        for v in order[1:]:
            lower = sd.bisect_left(v) - 1
            higher = lower + 1
            depth = 1 + max(sd.values()[lower], sd.values()[higher])
            ans = max(ans, depth)
            sd[v] = depth
        return ans

Java

class Solution {
    public int maxDepthBST(int[] order) {
        TreeMap<Integer, Integer> tm = new TreeMap<>();
        tm.put(0, 0);
        tm.put(Integer.MAX_VALUE, 0);
        tm.put(order[0], 1);
        int ans = 1;
        for (int i = 1; i < order.length; ++i) {
            int v = order[i];
            Map.Entry<Integer, Integer> lower = tm.lowerEntry(v);
            Map.Entry<Integer, Integer> higher = tm.higherEntry(v);
            int depth = 1 + Math.max(lower.getValue(), higher.getValue());
            ans = Math.max(ans, depth);
            tm.put(v, depth);
        }
        return ans;
    }
}

...