README.md

1579. 保证图可完全遍历

English Version

题目描述

Alice 和 Bob 共有一个无向图，其中包含 n 个节点和 3  种类型的边：

• 类型 1：只能由 Alice 遍历。
• 类型 2：只能由 Bob 遍历。
• 类型 3：Alice 和 Bob 都可以遍历。

给你一个数组 edges ，其中 edges[i] = [typei, ui, vi] 表示节点 ui 和 vi 之间存在类型为 typei 的双向边。请你在保证图仍能够被 Alice和 Bob 完全遍历的前提下，找出可以删除的最大边数。如果从任何节点开始，Alice 和 Bob 都可以到达所有其他节点，则认为图是可以完全遍历的。

返回可以删除的最大边数，如果 Alice 和 Bob 无法完全遍历图，则返回 -1 。

 

示例 1：

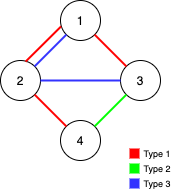
输入：n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
输出：2
解释：如果删除 [1,1,2] 和 [1,1,3] 这两条边，Alice 和 Bob 仍然可以完全遍历这个图。再删除任何其他的边都无法保证图可以完全遍历。所以可以删除的最大边数是 2 。

示例 2：

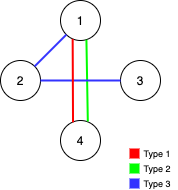
输入：n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
输出：0
解释：注意，删除任何一条边都会使 Alice 和 Bob 无法完全遍历这个图。

示例 3：

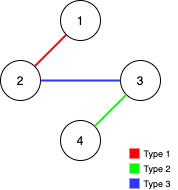
输入：n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
输出：-1
解释：在当前图中，Alice 无法从其他节点到达节点 4 。类似地，Bob 也不能达到节点 1 。因此，图无法完全遍历。

 

提示：

• 1 <= n <= 10^5
• 1 <= edges.length <= min(10^5, 3 * n * (n-1) / 2)
• edges[i].length == 3
• 1 <= edges[i][0] <= 3
• 1 <= edges[i][1] < edges[i][2] <= n
• 所有元组 (typei, ui, vi) 互不相同

解法

并查集。对于本题，构造两个并查集。同时操作两个并查集 ufa, ufb，遵从优先添加公共边的策略，即：优先添加 type = 3 的边。添加的过程中，若两点已连通，则累加多余的边 ans。

然后遍历 type = 1 的边添加到 ufa 中，而 type = 2 的边则添加到 ufb 中。此过程同样判断两点是否已连通，若是，则累加多余的边 ans。

最后判断两个并查集是否都只有一个连通分量，若是，返回 ans，否则返回 -1。

以下是并查集的几个常用模板。

模板 1——朴素并查集：

# 初始化，p存储每个点的父节点
p = list(range(n))
# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        # 路径压缩
        p[x] = find(p[x])
    return p[x]


# 合并a和b所在的两个集合
p[find(a)] = find(b)

模板 2——维护 size 的并查集：

# 初始化，p存储每个点的父节点，size只有当节点是祖宗节点时才有意义，表示祖宗节点所在集合中，点的数量
p = list(range(n))
size = [1] * n
# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        # 路径压缩
        p[x] = find(p[x])
    return p[x]
# 合并a和b所在的两个集合
if find(a) != find(b):
    size[find(b)] += size[find(a)]
    p[find(a)] = find(b)

模板 3——维护到祖宗节点距离的并查集：

# 初始化，p存储每个点的父节点，d[x]存储x到p[x]的距离
p = list(range(n))
d = [0] * n
# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        t = find(p[x])
        d[x] += d[p[x]]
        p[x] = t
    return p[x]
# 合并a和b所在的两个集合
p[find(a)] = find(b)
d[find(a)] = distance

Python3

class UnionFind:
    def __init__(self, n):
        self.p = list(range(n))
        self.n = n

    def union(self, a, b):
        pa, pb = self.find(a - 1), self.find(b - 1)
        if pa == pb:
            return False
        self.p[pa] = pb
        self.n -= 1
        return True

    def find(self, x):
        if self.p[x] != x:
            self.p[x] = self.find(self.p[x])
        return self.p[x]


class Solution:
    def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:
        ufa, ufb = UnionFind(n), UnionFind(n)
        ans = 0
        for t, u, v in edges:
            if t == 3:
                if ufa.union(u, v):
                    ufb.union(u, v)
                else:
                    ans += 1
        ans += sum((t == 1 and not ufa.union(u, v))
                   or (t == 2 and not ufb.union(u, v)) for t, u, v in edges)
        return ans if ufa.n == 1 and ufb.n == 1 else -1

Java

class Solution {
    public int maxNumEdgesToRemove(int n, int[][] edges) {
        UnionFind ufa = new UnionFind(n);
        UnionFind ufb = new UnionFind(n);
        int ans = 0;
        for (int[] e : edges) {
            if (e[0] == 3) {
                if (ufa.union(e[1], e[2])) {
                    ufb.union(e[1], e[2]);
                } else {
                    ++ans;
                }
            }
        }
        for (int[] e : edges) {
            if ((e[0] == 1 && !ufa.union(e[1], e[2])) || (e[0] == 2 && !ufb.union(e[1], e[2]))) {
                ++ans;
            }
        }
        return ufa.n == 1 && ufb.n == 1 ? ans : -1;
    }
}

class UnionFind {
    public int[] p;
    public int n;

    public UnionFind(int n) {
        p = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
        }
        this.n = n;
    }

    public boolean union(int a, int b) {
        int pa = find(a - 1);
        int pb = find(b - 1);
        if (pa == pb) {
            return false;
        }
        p[pa] = pb;
        --n;
        return true;
    }

    public int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}

C++

class UnionFind {
public:
    vector<int> p;
    int n;

    UnionFind(int _n)
        : n(_n)
        , p(_n) {
        iota(p.begin(), p.end(), 0);
    }

    bool unite(int a, int b) {
        int pa = find(a - 1), pb = find(b - 1);
        if (pa == pb) return false;
        p[pa] = pb;
        --n;
        return true;
    }

    int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }
};

class Solution {
public:
    int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {
        UnionFind ufa(n), ufb(n);
        int ans = 0;
        for (auto& e : edges) {
            if (e[0] == 3) {
                if (ufa.unite(e[1], e[2]))
                    ufb.unite(e[1], e[2]);
                else
                    ++ans;
            }
        }
        for (auto& e : edges)
            if ((e[0] == 1 && !ufa.unite(e[1], e[2])) || (e[0] == 2 && !ufb.unite(e[1], e[2])))
                ++ans;
        return ufa.n == 1 && ufb.n == 1 ? ans : -1;
    }
};

Go

type unionFind struct {
	p []int
	n int
}

func newUnionFind(n int) *unionFind {
	p := make([]int, n)
	for i := range p {
		p[i] = i
	}
	return &unionFind{p, n}
}

func (uf *unionFind) find(x int) int {
	if uf.p[x] != x {
		uf.p[x] = uf.find(uf.p[x])
	}
	return uf.p[x]
}

func (uf *unionFind) union(a, b int) bool {
	pa, pb := uf.find(a-1), uf.find(b-1)
	if pa == pb {
		return false
	}
	uf.p[pa] = pb
	uf.n--
	return true
}

func maxNumEdgesToRemove(n int, edges [][]int) int {
	ufa, ufb := newUnionFind(n), newUnionFind(n)
	ans := 0
	for _, e := range edges {
		if e[0] == 3 {
			if ufa.union(e[1], e[2]) {
				ufb.union(e[1], e[2])
			} else {
				ans++
			}
		}
	}
	for _, e := range edges {
		if (e[0] == 1 && !ufa.union(e[1], e[2])) || (e[0] == 2 && !ufb.union(e[1], e[2])) {
			ans++
		}
	}
	if ufa.n == 1 && ufb.n == 1 {
		return ans
	}
	return -1
}

...