README.md

1568. 使陆地分离的最少天数

English Version

题目描述

给你一个大小为 m x n ，由若干 0 和 1 组成的二维网格 grid ，其中 1 表示陆地， 0 表示水。岛屿 由水平方向或竖直方向上相邻的 1 （陆地）连接形成。

如果 恰好只有一座岛屿 ，则认为陆地是 连通的 ；否则，陆地就是 分离的 。

一天内，可以将 任何单个 陆地单元（1）更改为水单元（0）。

返回使陆地分离的最少天数。

 

示例 1：

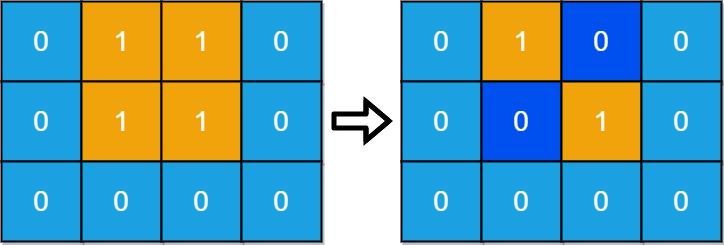
输入：grid = [[0,1,1,0],[0,1,1,0],[0,0,0,0]]
输出：2
解释：至少需要 2 天才能得到分离的陆地。
将陆地 grid[1][1] 和 grid[0][2] 更改为水，得到两个分离的岛屿。

示例 2：

输入：grid = [[1,1]]
输出：2
解释：如果网格中都是水，也认为是分离的 ([[1,1]] -> [[0,0]])，0 岛屿。

 

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 30
• grid[i][j] 为 0 或 1

解法

方法一：脑筋急转弯

观察发现，我们总是可以通过把角落相邻的两个陆地变成水，使得岛屿分离。因此，答案只可能是 0，1 或 2。

我们跑一遍 DFS，统计当前岛屿的数量，如果数量不等于 $1$，也就是说不满足恰好只有一座岛屿，那么答案就是 0。

否则，我们遍历每一块陆地，把它变成水，然后再跑一遍 DFS，看看岛屿的数量是否不等于 1，如果不等于 1，说明这块陆地变成水后，岛屿分离了，答案就是 1。

遍历结束，说明必须要把两块陆地变成水，才能使得岛屿分离，因此答案就是 2。

时间复杂度 $O(m^2\times n^2)$，其中 $m$ 和 $n$ 分别是 grid 的行数和列数。

Python3

class Solution:
    def minDays(self, grid: List[List[int]]) -> int:
        if self.count(grid) != 1:
            return 0
        m, n = len(grid), len(grid[0])
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 1:
                    grid[i][j] = 0
                    if self.count(grid) != 1:
                        return 1
                    grid[i][j] = 1
        return 2

    def count(self, grid):
        def dfs(i, j):
            grid[i][j] = 2
            for a, b in [[0, -1], [0, 1], [1, 0], [-1, 0]]:
                x, y = i + a, j + b
                if 0 <= x < m and 0 <= y < n and grid[x][y] == 1:
                    dfs(x, y)

        m, n = len(grid), len(grid[0])
        cnt = 0
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 1:
                    dfs(i, j)
                    cnt += 1
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 2:
                    grid[i][j] = 1
        return cnt

Java

class Solution {
    private static final int[] DIRS = new int[] {-1, 0, 1, 0, -1};
    private int[][] grid;
    private int m;
    private int n;

    public int minDays(int[][] grid) {
        this.grid = grid;
        m = grid.length;
        n = grid[0].length;
        if (count() != 1) {
            return 0;
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1) {
                    grid[i][j] = 0;
                    if (count() != 1) {
                        return 1;
                    }
                    grid[i][j] = 1;
                }
            }
        }
        return 2;
    }

    private int count() {
        int cnt = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1) {
                    dfs(i, j);
                    ++cnt;
                }
            }
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 2) {
                    grid[i][j] = 1;
                }
            }
        }
        return cnt;
    }

    private void dfs(int i, int j) {
        grid[i][j] = 2;
        for (int k = 0; k < 4; ++k) {
            int x = i + DIRS[k], y = j + DIRS[k + 1];
            if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1) {
                dfs(x, y);
            }
        }
    }
}

C++

class Solution {
public:
    const vector<int> dirs = {-1, 0, 1, 0, -1};
    int m, n;

    int minDays(vector<vector<int>>& grid) {
        m = grid.size(), n = grid[0].size();
        if (count(grid) != 1) {
            return 0;
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1) {
                    grid[i][j] = 0;
                    if (count(grid) != 1) {
                        return 1;
                    }
                    grid[i][j] = 1;
                }
            }
        }
        return 2;
    }

    int count(vector<vector<int>>& grid) {
        int cnt = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1) {
                    dfs(i, j, grid);
                    ++cnt;
                }
            }
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 2) {
                    grid[i][j] = 1;
                }
            }
        }
        return cnt;
    }

    void dfs(int i, int j, vector<vector<int>>& grid) {
        grid[i][j] = 2;
        for (int k = 0; k < 4; ++k) {
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1) {
                dfs(x, y, grid);
            }
        }
    }
};

Go

func minDays(grid [][]int) int {
	m, n := len(grid), len(grid[0])
	dirs := []int{-1, 0, 1, 0, -1}

	var dfs func(i, j int)
	dfs = func(i, j int) {
		grid[i][j] = 2
		for k := 0; k < 4; k++ {
			x, y := i+dirs[k], j+dirs[k+1]
			if x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 {
				dfs(x, y)
			}
		}
	}

	count := func() int {
		cnt := 0
		for i := 0; i < m; i++ {
			for j := 0; j < n; j++ {
				if grid[i][j] == 1 {
					dfs(i, j)
					cnt++
				}
			}
		}
		for i := 0; i < m; i++ {
			for j := 0; j < n; j++ {
				if grid[i][j] == 2 {
					grid[i][j] = 1
				}
			}
		}
		return cnt
	}

	if count() != 1 {
		return 0
	}
	for i := 0; i < m; i++ {
		for j := 0; j < n; j++ {
			if grid[i][j] == 1 {
				grid[i][j] = 0
				if count() != 1 {
					return 1
				}
				grid[i][j] = 1
			}
		}
	}
	return 2
}

...