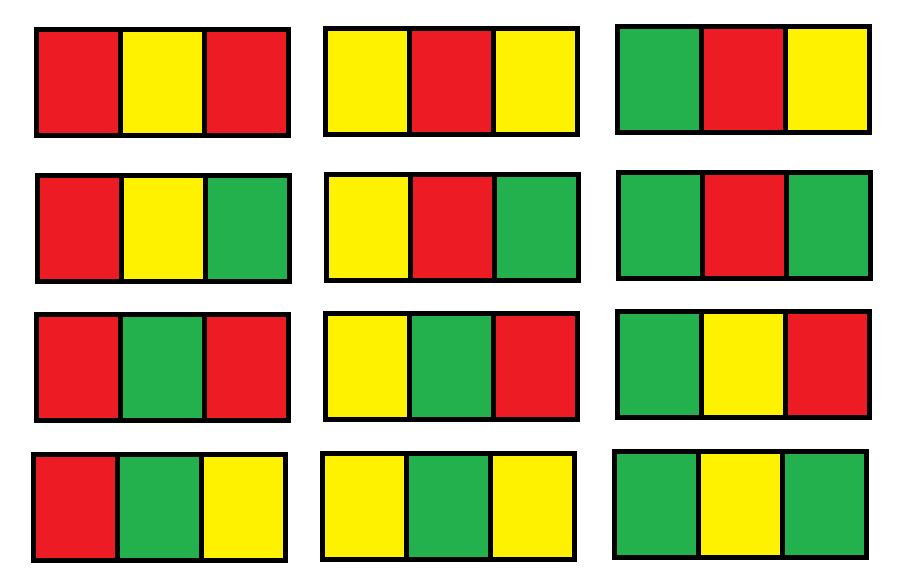
你有一个 n x 3 的网格图 grid ,你需要用 红,黄,绿 三种颜色之一给每一个格子上色,且确保相邻格子颜色不同(也就是有相同水平边或者垂直边的格子颜色不同)。
给你网格图的行数 n 。
请你返回给 grid 涂色的方案数。由于答案可能会非常大,请你返回答案对 10^9 + 7 取余的结果。
示例 1:
输入:n = 1 输出:12 解释:总共有 12 种可行的方法: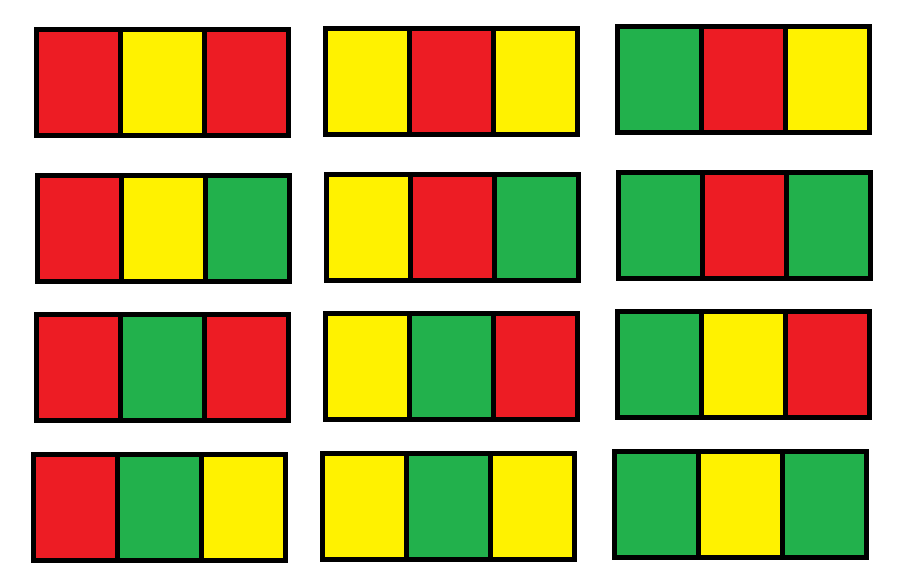
示例 2:
输入:n = 2 输出:54
示例 3:
输入:n = 3 输出:246
示例 4:
输入:n = 7 输出:106494
示例 5:
输入:n = 5000 输出:30228214
提示:
n == grid.lengthgrid[i].length == 31 <= n <= 5000
方法一:递推
把每一行所有可能的状态进行分类。根据对称性原理,当一行只有
- 当状态为
$010$ 型时:下一行可能的状态为:$101$,$102$ ,$121$ ,$201$ ,$202$ 。这$5$ 个状态可归纳为$3$ 个$010$ 型,$2$ 个$012$ 型。 - 当状态为
$012$ 型时:下一行可能的状态为:$101$,$120$ ,$121$ ,$201$ 。这$4$ 个状态可归纳为$2$ 个$010$ 型,$2$ 个$012$ 型。
综上所述,可以得到:$newf0 = 3 * f0 + 2 * f1$,$newf1 = 2 * f0 + 2 * f1$。
时间复杂度
class Solution:
def numOfWays(self, n: int) -> int:
mod = 10**9 + 7
f0 = f1 = 6
for _ in range(n - 1):
g0 = (3 * f0 + 2 * f1) % mod
g1 = (2 * f0 + 2 * f1) % mod
f0, f1 = g0, g1
return (f0 + f1) % modclass Solution {
public int numOfWays(int n) {
int mod = (int) 1e9 + 7;
long f0 = 6, f1 = 6;
for (int i = 0; i < n - 1; ++i) {
long g0 = (3 * f0 + 2 * f1) % mod;
long g1 = (2 * f0 + 2 * f1) % mod;
f0 = g0;
f1 = g1;
}
return (int) (f0 + f1) % mod;
}
}using ll = long long;
class Solution {
public:
int numOfWays(int n) {
int mod = 1e9 + 7;
ll f0 = 6, f1 = 6;
while (--n) {
ll g0 = (f0 * 3 + f1 * 2) % mod;
ll g1 = (f0 * 2 + f1 * 2) % mod;
f0 = g0;
f1 = g1;
}
return (int)(f0 + f1) % mod;
}
};func numOfWays(n int) int {
mod := int(1e9) + 7
f0, f1 := 6, 6
for n > 1 {
n--
g0 := (f0*3 + f1*2) % mod
g1 := (f0*2 + f1*2) % mod
f0, f1 = g0, g1
}
return (f0 + f1) % mod
}