二维矩阵 grid 由 0 (土地)和 1 (水)组成。岛是由最大的4个方向连通的 0 组成的群,封闭岛是一个 完全 由1包围(左、上、右、下)的岛。
请返回 封闭岛屿 的数目。
示例 1:
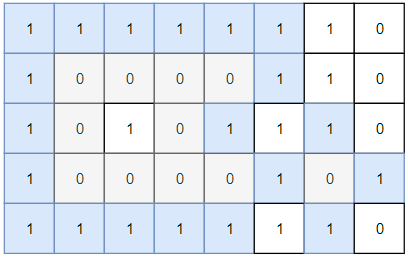
输入:grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]] 输出:2 解释: 灰色区域的岛屿是封闭岛屿,因为这座岛屿完全被水域包围(即被 1 区域包围)。
示例 2:
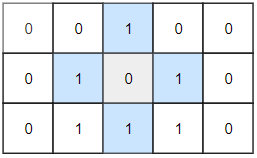
输入:grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]] 输出:1
示例 3:
输入:grid = [[1,1,1,1,1,1,1],
[1,0,0,0,0,0,1],
[1,0,1,1,1,0,1],
[1,0,1,0,1,0,1],
[1,0,1,1,1,0,1],
[1,0,0,0,0,0,1],
[1,1,1,1,1,1,1]]
输出:2
提示:
1 <= grid.length, grid[0].length <= 1000 <= grid[i][j] <=1
并查集。
并查集模板:
模板 1——朴素并查集:
# 初始化,p存储每个点的父节点
p = list(range(n))
# 返回x的祖宗节点
def find(x):
if p[x] != x:
# 路径压缩
p[x] = find(p[x])
return p[x]
# 合并a和b所在的两个集合
p[find(a)] = find(b)模板 2——维护 size 的并查集:
# 初始化,p存储每个点的父节点,size只有当节点是祖宗节点时才有意义,表示祖宗节点所在集合中,点的数量
p = list(range(n))
size = [1] * n
# 返回x的祖宗节点
def find(x):
if p[x] != x:
# 路径压缩
p[x] = find(p[x])
return p[x]
# 合并a和b所在的两个集合
if find(a) != find(b):
size[find(b)] += size[find(a)]
p[find(a)] = find(b)模板 3——维护到祖宗节点距离的并查集:
# 初始化,p存储每个点的父节点,d[x]存储x到p[x]的距离
p = list(range(n))
d = [0] * n
# 返回x的祖宗节点
def find(x):
if p[x] != x:
t = find(p[x])
d[x] += d[p[x]]
p[x] = t
return p[x]
# 合并a和b所在的两个集合
p[find(a)] = find(b)
d[find(a)] = distance本题与常规并查集统计岛屿题其实差不多,不同之处在于:增加了检测岛屿是否接触边缘的操作。
class Solution:
def closedIsland(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
p = list(range(m * n))
def find(x):
if p[x] != x:
p[x] = find(p[x])
return p[x]
for i in range(m):
for j in range(n):
if grid[i][j] == 1:
continue
idx = i * n + j
if i < m - 1 and grid[i + 1][j] == 0:
p[find(idx)] = find((i + 1) * n + j)
if j < n - 1 and grid[i][j + 1] == 0:
p[find(idx)] = find(i * n + j + 1)
s = [0] * (m * n)
for i in range(m):
for j in range(n):
if grid[i][j] == 0:
s[find(i * n + j)] = 1
for i in range(m):
for j in range(n):
root = find(i * n + j)
if not s[root]:
continue
if i == 0 or i == m - 1 or j == 0 or j == n - 1:
s[root] = 0
return sum(s)class Solution {
private int[] p;
public int closedIsland(int[][] grid) {
int m = grid.length, n = grid[0].length;
p = new int[m * n];
for (int i = 0; i < m * n; ++i) {
p[i] = i;
}
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 1) {
continue;
}
int idx = i * n + j;
if (i < m - 1 && grid[i + 1][j] == 0) {
p[find(idx)] = find((i + 1) * n + j);
}
if (j < n - 1 && grid[i][j + 1] == 0) {
p[find(idx)] = find(i * n + j + 1);
}
}
}
boolean[] s = new boolean[m * n];
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 0) {
s[find(i * n + j)] = true;
}
}
}
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
int root = find(i * n + j);
if (!s[root]) {
continue;
}
if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
s[root] = false;
}
}
}
int res = 0;
for (int i = 0; i < m * n; ++i) {
if (s[i]) {
++res;
}
}
return res;
}
private int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
}class Solution {
public:
vector<int> p;
int closedIsland(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
p.resize(m * n);
for (int i = 0; i < m * n; ++i) p[i] = i;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 1) continue;
int idx = i * n + j;
if (i < m - 1 && grid[i + 1][j] == 0) p[find(idx)] = find((i + 1) * n + j);
if (j < n - 1 && grid[i][j + 1] == 0) p[find(idx)] = find(i * n + j + 1);
}
}
vector<bool> s(m * n, false);
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 0) s[find(i * n + j)] = true;
}
}
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
int root = find(i * n + j);
if (!s[root]) continue;
if (i == 0 || i == m - 1 || j == 0 || j == n - 1) s[root] = false;
}
}
int res = 0;
for (auto e : s) {
if (e) ++res;
}
return res;
}
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
};var p []int
func closedIsland(grid [][]int) int {
m, n := len(grid), len(grid[0])
p = make([]int, m*n)
for i := 0; i < len(p); i++ {
p[i] = i
}
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
if grid[i][j] == 1 {
continue
}
idx := i*n + j
if i < m-1 && grid[i+1][j] == 0 {
p[find(idx)] = find((i+1)*n + j)
}
if j < n-1 && grid[i][j+1] == 0 {
p[find(idx)] = find(i*n + j + 1)
}
}
}
s := make([]bool, m*n)
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
if grid[i][j] == 0 {
s[find(i*n+j)] = true
}
}
}
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
root := find(i*n + j)
if !s[root] {
continue
}
if i == 0 || i == m-1 || j == 0 || j == n-1 {
s[root] = false
}
}
}
res := 0
for _, e := range s {
if e {
res++
}
}
return res
}
func find(x int) int {
if p[x] != x {
p[x] = find(p[x])
}
return p[x]
}