You are given an integer length and an array updates where updates[i] = [startIdxi, endIdxi, inci].
You have an array arr of length length with all zeros, and you have some operation to apply on arr. In the ith operation, you should increment all the elements arr[startIdxi], arr[startIdxi + 1], ..., arr[endIdxi] by inci.
Return arr after applying all the updates.
Example 1:
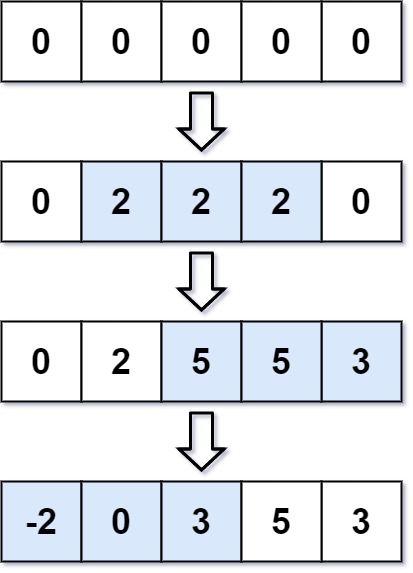
Input: length = 5, updates = [[1,3,2],[2,4,3],[0,2,-2]] Output: [-2,0,3,5,3]
Example 2:
Input: length = 10, updates = [[2,4,6],[5,6,8],[1,9,-4]] Output: [0,-4,2,2,2,4,4,-4,-4,-4]
Constraints:
1 <= length <= 1050 <= updates.length <= 1040 <= startIdxi <= endIdxi < length-1000 <= inci <= 1000
class Solution:
def getModifiedArray(self, length: int, updates: List[List[int]]) -> List[int]:
d = [0] * length
for l, r, c in updates:
d[l] += c
if r + 1 < length:
d[r + 1] -= c
return list(accumulate(d))class BinaryIndexedTree:
def __init__(self, n):
self.n = n
self.c = [0] * (n + 1)
@staticmethod
def lowbit(x):
return x & -x
def update(self, x, delta):
while x <= self.n:
self.c[x] += delta
x += BinaryIndexedTree.lowbit(x)
def query(self, x):
s = 0
while x:
s += self.c[x]
x -= BinaryIndexedTree.lowbit(x)
return s
class Solution:
def getModifiedArray(self, length: int, updates: List[List[int]]) -> List[int]:
tree = BinaryIndexedTree(length)
for start, end, inc in updates:
tree.update(start + 1, inc)
tree.update(end + 2, -inc)
return [tree.query(i + 1) for i in range(length)]class Solution {
public int[] getModifiedArray(int length, int[][] updates) {
int[] d = new int[length];
for (var e : updates) {
int l = e[0], r = e[1], c = e[2];
d[l] += c;
if (r + 1 < length) {
d[r + 1] -= c;
}
}
for (int i = 1; i < length; ++i) {
d[i] += d[i - 1];
}
return d;
}
}class Solution {
public int[] getModifiedArray(int length, int[][] updates) {
BinaryIndexedTree tree = new BinaryIndexedTree(length);
for (int[] e : updates) {
int start = e[0], end = e[1], inc = e[2];
tree.update(start + 1, inc);
tree.update(end + 2, -inc);
}
int[] ans = new int[length];
for (int i = 0; i < length; ++i) {
ans[i] = tree.query(i + 1);
}
return ans;
}
}
class BinaryIndexedTree {
private int n;
private int[] c;
public BinaryIndexedTree(int n) {
this.n = n;
c = new int[n + 1];
}
public void update(int x, int delta) {
while (x <= n) {
c[x] += delta;
x += lowbit(x);
}
}
public int query(int x) {
int s = 0;
while (x > 0) {
s += c[x];
x -= lowbit(x);
}
return s;
}
public static int lowbit(int x) {
return x & -x;
}
}class Solution {
public:
vector<int> getModifiedArray(int length, vector<vector<int>>& updates) {
vector<int> d(length);
for (auto& e : updates) {
int l = e[0], r = e[1], c = e[2];
d[l] += c;
if (r + 1 < length) d[r + 1] -= c;
}
for (int i = 1; i < length; ++i) d[i] += d[i - 1];
return d;
}
};class BinaryIndexedTree {
public:
int n;
vector<int> c;
BinaryIndexedTree(int _n): n(_n), c(_n + 1){}
void update(int x, int delta) {
while (x <= n)
{
c[x] += delta;
x += lowbit(x);
}
}
int query(int x) {
int s = 0;
while (x > 0)
{
s += c[x];
x -= lowbit(x);
}
return s;
}
int lowbit(int x) {
return x & -x;
}
};
class Solution {
public:
vector<int> getModifiedArray(int length, vector<vector<int>>& updates) {
BinaryIndexedTree* tree = new BinaryIndexedTree(length);
for (auto& e : updates)
{
int start = e[0], end = e[1], inc = e[2];
tree->update(start + 1, inc);
tree->update(end + 2, -inc);
}
vector<int> ans;
for (int i = 0; i < length; ++i) ans.push_back(tree->query(i + 1));
return ans;
}
};func getModifiedArray(length int, updates [][]int) []int {
d := make([]int, length)
for _, e := range updates {
l, r, c := e[0], e[1], e[2]
d[l] += c
if r+1 < length {
d[r+1] -= c
}
}
for i := 1; i < length; i++ {
d[i] += d[i-1]
}
return d
}type BinaryIndexedTree struct {
n int
c []int
}
func newBinaryIndexedTree(n int) *BinaryIndexedTree {
c := make([]int, n+1)
return &BinaryIndexedTree{n, c}
}
func (this *BinaryIndexedTree) lowbit(x int) int {
return x & -x
}
func (this *BinaryIndexedTree) update(x, delta int) {
for x <= this.n {
this.c[x] += delta
x += this.lowbit(x)
}
}
func (this *BinaryIndexedTree) query(x int) int {
s := 0
for x > 0 {
s += this.c[x]
x -= this.lowbit(x)
}
return s
}
func getModifiedArray(length int, updates [][]int) []int {
tree := newBinaryIndexedTree(length)
for _, e := range updates {
start, end, inc := e[0], e[1], e[2]
tree.update(start+1, inc)
tree.update(end+2, -inc)
}
ans := make([]int, length)
for i := range ans {
ans[i] = tree.query(i + 1)
}
return ans
}/**
* @param {number} length
* @param {number[][]} updates
* @return {number[]}
*/
var getModifiedArray = function (length, updates) {
const d = new Array(length).fill(0);
for (const [l, r, c] of updates) {
d[l] += c;
if (r + 1 < length) {
d[r + 1] -= c;
}
}
for (let i = 1; i < length; ++i) {
d[i] += d[i - 1];
}
return d;
};