Skip to content

Latest commit

 

History

History
611 lines (508 loc) · 15.1 KB

README_EN.md

File metadata and controls

611 lines (508 loc) · 15.1 KB
Raw

308. Range Sum Query 2D - Mutable

中文文档

Description

Given a 2D matrix matrix, handle multiple queries of the following types:

  1. Update the value of a cell in matrix.
  2. Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Implement the NumMatrix class:

  • NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
  • void update(int row, int col, int val) Updates the value of matrix[row][col] to be val.
  • int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

 

Example 1:

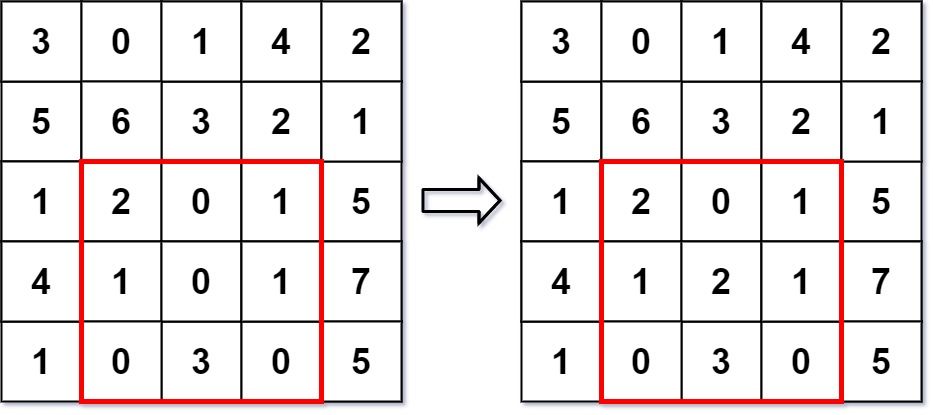
Input
["NumMatrix", "sumRegion", "update", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [3, 2, 2], [2, 1, 4, 3]]
Output
[null, 8, null, 10]

Explanation
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e. sum of the left red rectangle)
numMatrix.update(3, 2, 2); // matrix changes from left image to right image
numMatrix.sumRegion(2, 1, 4, 3); // return 10 (i.e. sum of the right red rectangle)

 

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 200
  • -1000 <= matrix[i][j] <= 1000
  • 0 <= row < m
  • 0 <= col < n
  • -1000 <= val <= 1000
  • 0 <= row1 <= row2 < m
  • 0 <= col1 <= col2 < n
  • At most 5000 calls will be made to sumRegion and update.

Solutions

Binary Indexed Tree or Segment Tree.

Python3

Binary Indexed Tree:

class BinaryIndexedTree:
    def __init__(self, n):
        self.n = n
        self.c = [0] * (n + 1)

    @staticmethod
    def lowbit(x):
        return x & -x

    def update(self, x, delta):
        while x <= self.n:
            self.c[x] += delta
            x += BinaryIndexedTree.lowbit(x)

    def query(self, x):
        s = 0
        while x > 0:
            s += self.c[x]
            x -= BinaryIndexedTree.lowbit(x)
        return s


class NumMatrix:
    def __init__(self, matrix: List[List[int]]):
        self.trees = []
        n = len(matrix[0])
        for row in matrix:
            tree = BinaryIndexedTree(n)
            for j, v in enumerate(row):
                tree.update(j + 1, v)
            self.trees.append(tree)

    def update(self, row: int, col: int, val: int) -> None:
        tree = self.trees[row]
        prev = tree.query(col + 1) - tree.query(col)
        tree.update(col + 1, val - prev)

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        return sum(
            tree.query(col2 + 1) - tree.query(col1)
            for tree in self.trees[row1 : row2 + 1]
        )


# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# obj.update(row,col,val)
# param_2 = obj.sumRegion(row1,col1,row2,col2)
class Node:
    def __init__(self):
        self.l = 0
        self.r = 0
        self.v = 0

class SegmentTree:
    def __init__(self, nums):
        n = len(nums)
        self.nums = nums
        self.tr = [Node() for _ in range(4 * n)]
        self.build(1, 1, n)

    def build(self, u, l, r):
        self.tr[u].l = l
        self.tr[u].r = r
        if l == r:
            self.tr[u].v = self.nums[l - 1]
            return
        mid = (l + r) >> 1
        self.build(u << 1, l, mid)
        self.build(u << 1 | 1, mid + 1, r)
        self.pushup(u)

    def modify(self, u, x, v):
        if self.tr[u].l == x and self.tr[u].r == x:
            self.tr[u].v = v
            return
        mid = (self.tr[u].l + self.tr[u].r) >> 1
        if x <= mid:
            self.modify(u << 1, x, v)
        else:
            self.modify(u << 1 | 1, x, v)
        self.pushup(u)

    def query(self, u, l, r):
        if self.tr[u].l >= l and self.tr[u].r <= r:
            return self.tr[u].v
        mid = (self.tr[u].l + self.tr[u].r) >> 1
        v = 0
        if l <= mid:
            v += self.query(u << 1, l, r)
        if r > mid:
            v += self.query(u << 1 | 1, l, r)
        return v

    def pushup(self, u):
        self.tr[u].v = self.tr[u << 1].v + self.tr[u << 1 | 1].v

class NumMatrix:

    def __init__(self, matrix: List[List[int]]):
        self.trees = [SegmentTree(row) for row in matrix]

    def update(self, row: int, col: int, val: int) -> None:
        tree = self.trees[row]
        tree.modify(1, col + 1, val)

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        return sum(self.trees[row].query(1, col1 + 1, col2 + 1) for row in range(row1, row2 + 1))


# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# obj.update(row,col,val)
# param_2 = obj.sumRegion(row1,col1,row2,col2)

Java

Binary Indexed Tree:

class BinaryIndexedTree {
    private int n;
    private int[] c;

    public BinaryIndexedTree(int n) {
        this.n = n;
        c = new int[n + 1];
    }

    public void update(int x, int delta) {
        while (x <= n) {
            c[x] += delta;
            x += lowbit(x);
        }
    }

    public int query(int x) {
        int s = 0;
        while (x > 0) {
            s += c[x];
            x -= lowbit(x);
        }
        return s;
    }

    public static int lowbit(int x) {
        return x & -x;
    }
}

class NumMatrix {
    private BinaryIndexedTree[] trees;

    public NumMatrix(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        trees = new BinaryIndexedTree[m];
        for (int i = 0; i < m; ++i) {
            BinaryIndexedTree tree = new BinaryIndexedTree(n);
            for (int j = 0; j < n; ++j) {
                tree.update(j + 1, matrix[i][j]);
            }
            trees[i] = tree;
        }
    }

    public void update(int row, int col, int val) {
        BinaryIndexedTree tree = trees[row];
        int prev = tree.query(col + 1) - tree.query(col);
        tree.update(col + 1, val - prev);
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        int s = 0;
        for (int i = row1; i <= row2; ++i) {
            BinaryIndexedTree tree = trees[i];
            s += tree.query(col2 + 1) - tree.query(col1);
        }
        return s;
    }
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * obj.update(row,col,val);
 * int param_2 = obj.sumRegion(row1,col1,row2,col2);
 */
class Node {
    int l;
    int r;
    int v;
}

class SegmentTree {
    private Node[] tr;
    private int[] nums;

    public SegmentTree(int[] nums) {
        int n = nums.length;
        tr = new Node[n << 2];
        this.nums = nums;
        for (int i = 0; i < tr.length; ++i) {
            tr[i] = new Node();
        }
        build(1, 1, n);
    }

    public void build(int u, int l, int r) {
        tr[u].l = l;
        tr[u].r = r;
        if (l == r) {
            tr[u].v = nums[l - 1];
            return;
        }
        int mid = (l + r) >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }

    public void modify(int u, int x, int v) {
        if (tr[u].l == x && tr[u].r == x) {
            tr[u].v = v;
            return;
        }
        int mid = (tr[u].l + tr[u].r) >> 1;
        if (x <= mid) {
            modify(u << 1, x, v);
        } else {
            modify(u << 1 | 1, x, v);
        }
        pushup(u);
    }

    public void pushup(int u) {
        tr[u].v = tr[u << 1].v + tr[u << 1 | 1].v;
    }

    public int query(int u, int l, int r) {
        if (tr[u].l >= l && tr[u].r <= r) {
            return tr[u].v;
        }
        int mid = (tr[u].l + tr[u].r) >> 1;
        int v = 0;
        if (l <= mid) {
            v += query(u << 1, l, r);
        }
        if (r > mid) {
            v += query(u << 1 | 1, l, r);
        }
        return v;
    }
}

class NumMatrix {
    private SegmentTree[] trees;

    public NumMatrix(int[][] matrix) {
        int m = matrix.length;
        trees = new SegmentTree[m];
        for (int i = 0; i < m; ++i) {
            trees[i] = new SegmentTree(matrix[i]);
        }
    }

    public void update(int row, int col, int val) {
        SegmentTree tree = trees[row];
        tree.modify(1, col + 1, val);
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        int s = 0;
        for (int row = row1; row <= row2; ++row) {
            SegmentTree tree = trees[row];
            s += tree.query(1, col1 + 1, col2 + 1);
        }
        return s;
    }
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * obj.update(row,col,val);
 * int param_2 = obj.sumRegion(row1,col1,row2,col2);
 */

C++

Binary Indexed Tree:

class BinaryIndexedTree {
public:
    int n;
    vector<int> c;

    BinaryIndexedTree(int _n)
        : n(_n)
        , c(_n + 1) { }

    void update(int x, int delta) {
        while (x <= n) {
            c[x] += delta;
            x += lowbit(x);
        }
    }

    int query(int x) {
        int s = 0;
        while (x > 0) {
            s += c[x];
            x -= lowbit(x);
        }
        return s;
    }

    int lowbit(int x) {
        return x & -x;
    }
};

class NumMatrix {
public:
    vector<BinaryIndexedTree*> trees;

    NumMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        trees.resize(m);
        for (int i = 0; i < m; ++i) {
            BinaryIndexedTree* tree = new BinaryIndexedTree(n);
            for (int j = 0; j < n; ++j) tree->update(j + 1, matrix[i][j]);
            trees[i] = tree;
        }
    }

    void update(int row, int col, int val) {
        BinaryIndexedTree* tree = trees[row];
        int prev = tree->query(col + 1) - tree->query(col);
        tree->update(col + 1, val - prev);
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        int s = 0;
        for (int i = row1; i <= row2; ++i) {
            BinaryIndexedTree* tree = trees[i];
            s += tree->query(col2 + 1) - tree->query(col1);
        }
        return s;
    }
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix* obj = new NumMatrix(matrix);
 * obj->update(row,col,val);
 * int param_2 = obj->sumRegion(row1,col1,row2,col2);
 */

Segment Tree:

class Node {
public:
    int l;
    int r;
    int v;
};

class SegmentTree {
public:
    vector<Node*> tr;
    vector<int> nums;

    SegmentTree(vector<int>& nums) {
        int n = nums.size();
        tr.resize(n << 2);
        this->nums = nums;
        for (int i = 0; i < tr.size(); ++i) tr[i] = new Node();
        build(1, 1, n);
    }

    void build(int u, int l, int r) {
        tr[u]->l = l;
        tr[u]->r = r;
        if (l == r)
        {
            tr[u]->v = nums[l - 1];
            return;
        }
        int mid = (l + r) >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }

    void modify(int u, int x, int v) {
        if (tr[u]->l == x && tr[u]->r == x)
        {
            tr[u]->v = v;
            return;
        }
        int mid = (tr[u]->l + tr[u]->r) >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }

    int query(int u, int l, int r) {
        if (tr[u]->l >= l && tr[u]->r <= r) return tr[u]->v;
        int mid = (tr[u]->l + tr[u]->r) >> 1;
        int v = 0;
        if (l <= mid) v += query(u << 1, l, r);
        if (r > mid) v += query(u << 1 | 1, l, r);
        return v;
    }

    void pushup(int u) {
        tr[u]->v = tr[u << 1]->v + tr[u << 1 | 1]->v;
    }
};

class NumMatrix {
public:
    vector<SegmentTree*> trees;

    NumMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size();
        trees.resize(m);
        for (int i = 0; i < m; ++i) trees[i] = new SegmentTree(matrix[i]);
    }

    void update(int row, int col, int val) {
        SegmentTree* tree = trees[row];
        tree->modify(1, col + 1, val);
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        int s = 0;
        for (int row = row1; row <= row2; ++row) s += trees[row]->query(1, col1 + 1, col2 + 1);
        return s;
    }
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix* obj = new NumMatrix(matrix);
 * obj->update(row,col,val);
 * int param_2 = obj->sumRegion(row1,col1,row2,col2);
 */

Go

Binary Indexed Tree:

type BinaryIndexedTree struct {
	n int
	c []int
}

func newBinaryIndexedTree(n int) *BinaryIndexedTree {
	c := make([]int, n+1)
	return &BinaryIndexedTree{n, c}
}

func (this *BinaryIndexedTree) lowbit(x int) int {
	return x & -x
}

func (this *BinaryIndexedTree) update(x, delta int) {
	for x <= this.n {
		this.c[x] += delta
		x += this.lowbit(x)
	}
}

func (this *BinaryIndexedTree) query(x int) int {
	s := 0
	for x > 0 {
		s += this.c[x]
		x -= this.lowbit(x)
	}
	return s
}

type NumMatrix struct {
	trees []*BinaryIndexedTree
}

func Constructor(matrix [][]int) NumMatrix {
	n := len(matrix[0])
	var trees []*BinaryIndexedTree
	for _, row := range matrix {
		tree := newBinaryIndexedTree(n)
		for j, v := range row {
			tree.update(j+1, v)
		}
		trees = append(trees, tree)
	}
	return NumMatrix{trees}
}

func (this *NumMatrix) Update(row int, col int, val int) {
	tree := this.trees[row]
	prev := tree.query(col+1) - tree.query(col)
	tree.update(col+1, val-prev)
}

func (this *NumMatrix) SumRegion(row1 int, col1 int, row2 int, col2 int) int {
	s := 0
	for i := row1; i <= row2; i++ {
		tree := this.trees[i]
		s += tree.query(col2+1) - tree.query(col1)
	}
	return s
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * obj := Constructor(matrix);
 * obj.Update(row,col,val);
 * param_2 := obj.SumRegion(row1,col1,row2,col2);
 */

...