二叉搜索树

简介

引用自：LeetCode官方

代码实现：TheStarBoys

二叉搜索树是二叉树的一种特殊形式。二叉搜索树具有以下性质：每个节点中的值必须大于（或等于）其左侧子树中的任何值，但小于（或等于）其右侧子树中的任何值。

此章至少需要的预备知识：

二叉树

定义

二叉搜索树（BST）是二叉树的一种特殊表示形式，它满足如下特性：

每个节点中的值必须大于（或等于）存储在其左侧子树中的任何值。
每个节点中的值必须小于（或等于）存储在其右子树中的任何值。

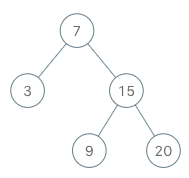
下面是一个二叉搜索树的例子：

数据结构定义

type TreeNode struct {
	Val int
	Left *TreeNode
	Right *TreeNode
}

复杂度分析

时间复杂度

以查找为例：

最坏时间复杂度：当根节点的左右子树极度不平衡，退化为链表的时候，查找的时间复杂度为 O(n)

最好时间复杂度：如果二叉搜索树是一颗完全二叉树（或满二叉树），其时间复杂度与树高度成正比，也就是 O(height)。

空间复杂度

跟元素的个数成正比，为 O(n)

二叉搜索树中的基本操作

验证二叉搜索树

题目描述

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

节点的左子树只包含小于当前节点的数。节点的右子树只包含大于当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。

示例 1:

输入:
    2
   / \
  1   3
输出: true

示例 2:

输入:
    5
   / \
  1   4
     / \
    3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
     根节点的值为 5 ，但是其右子节点值为 4 。

代码实现

思路一：利用中序遍历

func isValidBST(root *TreeNode) bool {
    if root == nil {
        return true
    }
    pre := -math.MaxInt64
    return isValid(root, &pre)
}

// 利用二叉搜索树的中序遍历是升序序列的特点
// 因此中序遍历二叉搜索树时，前面遍历过的值一定小于当前节点的值
func isValid(root *TreeNode, pre *int) bool {
    if root == nil {
        return true
    }
    if !isValid(root.Left, pre) {
        return false
    }
    if root.Val <= *pre {
        return false
    }
    *pre = root.Val
    if !isValid(root.Right, pre) {
        return false
    }
    return true
}

思路二：利用二叉搜索树特性

func isValidBST(root *TreeNode) bool {
	return isValidBSTByBorder(root, math.MaxInt64, math.MinInt64)
}

func isValidBSTByBorder(root *TreeNode, max,min int) bool {
	if root == nil {
		return true
	}

	if root.Val >= max || root.Val <= min {
		return false
	}
	
	return isValidBSTByBorder(root.Left, root.Val, min) &&
    	isValidBSTByBorder(root.Right, max, root.Val)
}

二叉搜索树迭代器

题目描述

实现一个二叉搜索树迭代器。你将使用二叉搜索树的根节点初始化迭代器。

调用 next() 将返回二叉搜索树中的下一个最小的数。

示例：

BSTIterator iterator = new BSTIterator(root);
iterator.next();    // 返回 3
iterator.next();    // 返回 7
iterator.hasNext(); // 返回 true
iterator.next();    // 返回 9
iterator.hasNext(); // 返回 true
iterator.next();    // 返回 15
iterator.hasNext(); // 返回 true
iterator.next();    // 返回 20
iterator.hasNext(); // 返回 false

提示：

next() 和 hasNext() 操作的时间复杂度是 O(1)，并使用 O(h) 内存，其中 h 是树的高度。你可以假设 next() 调用总是有效的，也就是说，当调用 next() 时，BST 中至少存在一个下一个最小的数。

代码实现

方法一：扁平化二叉搜索树

是一种实现思路，但不符合使用O(h)内存的条件

type BSTIterator struct {
	numList   []int
	nextIndex int
}

func Constructor(root *TreeNode) BSTIterator {
	Iterator := BSTIterator{
		numList:   make([]int, 0),
		nextIndex: 0,
	}
	inorder(root, &Iterator.numList)

	return Iterator
}

func inorder(root *TreeNode, numList *[]int) {
	if root == nil {
		return
	}
	inorder(root.Left, numList)
	*numList = append(*numList, root.Val)
	inorder(root.Right, numList)
}

/** @return the next smallest number */
func (this *BSTIterator) Next() int {
	if this.nextIndex > len(this.numList)-1 {
		return -1
	}
	res := this.numList[this.nextIndex]
	this.nextIndex++
	return res
}

/** @return whether we have a next smallest number */
func (this *BSTIterator) HasNext() bool {
	if this.nextIndex > len(this.numList)-1 {
		return false
	} else {
		return true
	}
}

方法二：受控递归

在二叉搜索树中实现搜索操作

题目描述

给定二叉搜索树（BST）的根节点和一个值。你需要在BST中找到节点值等于给定值的节点。返回以该节点为根的子树。如果节点不存在，则返回 NULL。

例如，

给定二叉搜索树:

你应该返回如下子树:

  2     
 / \   
1   3

在上述示例中，如果要找的值是 5，但因为没有节点值为 5，我们应该返回 NULL。

题目分析

二叉搜索树主要支持三个操作：搜索、插入和删除。在本章中，我们将讨论如何在二叉搜索树中搜索特定的值。

根据BST的特性，对于每个节点：

如果目标值等于节点的值，则返回节点;
如果目标值小于节点的值，则继续在左子树中搜索;
如果目标值大于节点的值，则继续在右子树中搜索。

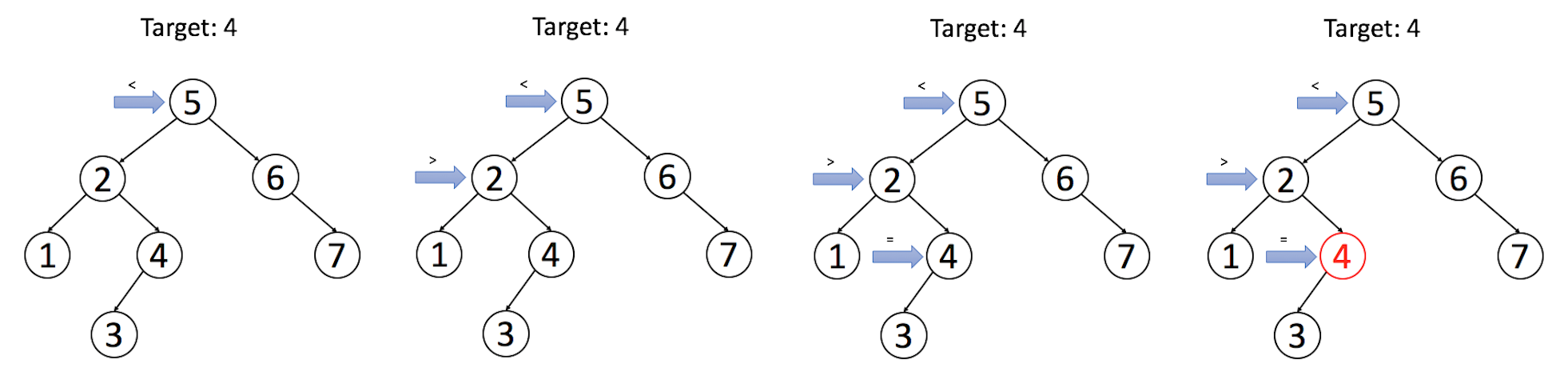
我们一起来看一个例子：我们在上面的二叉搜索树中搜索目标值为 4 的节点。

请在以下习题中，自己尝试实现搜索操作。你可以运用递归或迭代方法去解决这类问题，并尝试分析时间复杂度和空间复杂度。我们将在之后的文章介绍一个更好的解决方案。

代码实现

func searchBST(root *TreeNode, val int) *TreeNode {
	if root == nil {
		return nil
	}
  if root.Val == val {
		return root
	}
	if root.Val > val {
		return searchBST(root.Left, val)
	}
	return searchBST(root.Right, val)
}

在二叉搜索树中实现插入操作

题目描述

给定二叉搜索树（BST）的根节点和要插入树中的值，将值插入二叉搜索树。返回插入后二叉搜索树的根节点。保证原始二叉搜索树中不存在新值。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。你可以返回任意有效的结果。

例如,

给定二叉搜索树:
		4
   / \
  2   7
 / \
1   3

和 插入的值: 5

你可以返回这个二叉搜索树:

或者这个树也是有效的:

题目分析

二叉搜索树中的另一个常见操作是插入一个新节点。有许多不同的方法去插入新节点，这篇文章中，我们只讨论一种使整体操作变化最小的经典方法。它的主要思想是为目标节点找出合适的叶节点位置，然后将该节点作为叶节点插入。因此，搜索将成为插入的起始。

与搜索操作类似，对于每个节点，我们将：

根据节点值与目标节点值的关系，搜索左子树或右子树；
重复步骤 1 直到到达外部节点；
根据节点的值与目标节点的值的关系，将新节点添加为其左侧或右侧的子节点。

这样，我们就可以添加一个新的节点并依旧维持二叉搜索树的性质。

代码实现

方法一：递归

func insertIntoBST(root *TreeNode, val int) *TreeNode {
    // 插入的话，插入叶子节点一定是一种合法的可能
    if root==nil{
        return &TreeNode{Val:val}
    }
    if val>root.Val{
        root.Right=insertIntoBST(root.Right,val)
    }
    if val<root.Val{
        root.Left=insertIntoBST(root.Left, val)
    }
    return root
}

方法二：迭代

在二叉搜索树中实现删除操作

题目描述

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；如果找到了，删除它。说明：要求算法时间复杂度为 O(h)，h 为树的高度。

示例:

root = [5,3,6,2,4,null,7]
key = 3

    5
   / \
  3   6
 / \   \
2   4   7

给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。

一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。

    5
   / \
  4   6
 /     \
2       7

另一个正确答案是 [5,2,6,null,4,null,7]。

    5
   / \
  2   6
   \   \
    4   7

题目分析

删除要比我们前面提到过的两种操作复杂许多。有许多不同的删除节点的方法，这篇文章中，我们只讨论一种使整体操作变化最小的方法。我们的方案是用一个合适的子节点来替换要删除的目标节点。根据其子节点的个数，我们需考虑以下三种情况：

如果目标节点没有子节点，我们可以直接移除该目标节点。
如果目标节只有一个子节点，我们可以用其子节点作为替换。
如果目标节点有两个子节点，我们需要用其中序后继节点或者前驱节点来替换，再删除该目标节点。

我们来看下面这几个例子，以帮助你理解删除操作的中心思想：

例 1：目标节点没有子节点

例 2：目标节只有一个子节点

例 3：目标节点有两个子节点

通过理解以上的示例，你应该可以独立实现删除操作了。

代码实现

func deleteNode(root *TreeNode, key int) *TreeNode {
	if root == nil {
		return nil
	}
	//如果当前val 大于查找数  则往小的左边查找
	if root.Val > key {
		root.Left = deleteNode(root.Left, key)
		return root
  //如果当前val 小于查找数 则往右边查找
	} else if root.Val < key {
		root.Right = deleteNode(root.Right, key)
		return root
	} else {
		//找到的情况
		//左节点为空
		//左右为空的这种情况已经覆盖
		if root.Left == nil {
			//右节点替代
			right := root.Right
			//右节点置为 nil
			root.Right = nil
			return right
		}
		//右节点为空
		if root.Right == nil {
			//左节点替换
			left := root.Left
			//左节点为空
			root.Left = nil
			return left
		}
		//左右不为空的情况
		//这里使用前驱节点替换  找到比自己大的最小节点
		rMin := minRight(root.Right)
		//注意设置 左右节点的顺序不能改变
		//右边为删除前驱节点的新子树
		rMin.Right = delMinRight(root.Right)
		//左边节点不变
		rMin.Left = root.Left

		root.Left, root.Right = nil, nil
		return rMin
	}
}

func minRight(node *TreeNode) *TreeNode {
	if node.Left == nil {
		return node
	}
	return minRight(node.Left)
}

func delMinRight(node *TreeNode) *TreeNode {
	if node.Left == nil {
		//用右节点替换自己
		right := node.Right
		node.Right = nil
		return right
	}
	node.Left = delMinRight(node.Left)
	return node
}

二叉搜索树的最近公共祖先

题目描述

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。 p、q 为不同节点且均存在于给定的二叉搜索树中。

代码实现

func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
    if root == nil {
        return nil
    }
    if root == q {
        return q
    } else if root == p {
        return p
    }
    // 他们处于同一个子树中，其中一个结点将成为最近公共祖先
    if p.Val < root.Val && q.Val < root.Val {
        return lowestCommonAncestor(root.Left, p, q)
    }
    if p.Val > root.Val && q.Val > root.Val {
        return lowestCommonAncestor(root.Right, p, q)
    }
    // 该结点自身就是p, q的最近公共祖先
    return root
}

根据题意进行优化：

func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
    // 根据题意，p、q一定存在
    // 所以判断p、q是否各自在左、右子树中
    if p.Val < root.Val && q.Val > root.Val ||
        p.Val > root.Val && q.Val < root.Val {
        return root
    }
    // 最近公共祖先是节点本身
    if p == root || q == root {
        return root
    }

    // p、q在同一颗子树中的情况
    if p.Val < root.Val && q.Val < root.Val {
        return lowestCommonAncestor(root.Left, p, q)
    } else {
        return lowestCommonAncestor(root.Right, p, q)
    }
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

binarySearchTree.md

binarySearchTree.md

二叉搜索树

简介

定义

数据结构定义

复杂度分析

时间复杂度

空间复杂度

二叉搜索树中的基本操作

验证二叉搜索树

题目描述

代码实现

二叉搜索树迭代器

题目描述

代码实现

在二叉搜索树中实现搜索操作

题目描述

题目分析

代码实现

在二叉搜索树中实现插入操作

题目描述

题目分析

代码实现

在二叉搜索树中实现删除操作

题目描述

题目分析

代码实现

二叉搜索树的最近公共祖先

题目描述

代码实现

Files

binarySearchTree.md

Latest commit

History

binarySearchTree.md

File metadata and controls

二叉搜索树

简介

定义

数据结构定义

复杂度分析

时间复杂度

空间复杂度

二叉搜索树中的基本操作

验证二叉搜索树

题目描述

代码实现

二叉搜索树迭代器

题目描述

代码实现

在二叉搜索树中实现搜索操作

题目描述

题目分析

代码实现

在二叉搜索树中实现插入操作

题目描述

题目分析

代码实现

在二叉搜索树中实现删除操作

题目描述

题目分析

代码实现

二叉搜索树的最近公共祖先

题目描述

代码实现