-
Notifications
You must be signed in to change notification settings - Fork 0
/
db.json
1 lines (1 loc) · 391 KB
/
db.json
1
{"meta":{"version":1,"warehouse":"4.0.0"},"models":{"Asset":[{"_id":"source/CNAME","path":"CNAME","modified":0,"renderable":0},{"_id":"themes/hexo-theme-next-master/source/css/main.styl","path":"css/main.styl","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/images/algolia_logo.svg","path":"images/algolia_logo.svg","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/images/apple-touch-icon-next.png","path":"images/apple-touch-icon-next.png","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/images/avatar.gif","path":"images/avatar.gif","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/images/cc-by-nc-nd.svg","path":"images/cc-by-nc-nd.svg","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/images/cc-by-nc-sa.svg","path":"images/cc-by-nc-sa.svg","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/images/cc-by-nc.svg","path":"images/cc-by-nc.svg","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/images/cc-by-nd.svg","path":"images/cc-by-nd.svg","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/images/cc-by-sa.svg","path":"images/cc-by-sa.svg","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/images/cc-by.svg","path":"images/cc-by.svg","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/images/cc-zero.svg","path":"images/cc-zero.svg","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/images/favicon-16x16-next.png","path":"images/favicon-16x16-next.png","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/images/favicon-32x32-next.png","path":"images/favicon-32x32-next.png","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/images/logo.svg","path":"images/logo.svg","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/js/algolia-search.js","path":"js/algolia-search.js","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/js/bookmark.js","path":"js/bookmark.js","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/js/local-search.js","path":"js/local-search.js","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/js/motion.js","path":"js/motion.js","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/js/next-boot.js","path":"js/next-boot.js","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/js/utils.js","path":"js/utils.js","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/lib/anime.min.js","path":"lib/anime.min.js","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/js/schemes/pisces.js","path":"js/schemes/pisces.js","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/js/schemes/muse.js","path":"js/schemes/muse.js","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/lib/velocity/velocity.min.js","path":"lib/velocity/velocity.min.js","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/lib/velocity/velocity.ui.min.js","path":"lib/velocity/velocity.ui.min.js","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/lib/font-awesome/css/all.min.css","path":"lib/font-awesome/css/all.min.css","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/lib/font-awesome/webfonts/fa-brands-400.woff2","path":"lib/font-awesome/webfonts/fa-brands-400.woff2","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/lib/font-awesome/webfonts/fa-regular-400.woff2","path":"lib/font-awesome/webfonts/fa-regular-400.woff2","modified":0,"renderable":1},{"_id":"themes/hexo-theme-next-master/source/lib/font-awesome/webfonts/fa-solid-900.woff2","path":"lib/font-awesome/webfonts/fa-solid-900.woff2","modified":0,"renderable":1}],"Cache":[{"_id":"source/.DS_Store","hash":"406eb68229628ca2201fa362f2332462807592d0","modified":1642833964024},{"_id":"source/_posts/.DS_Store","hash":"511bec32511f46b25ccc60d3e12e603e35aefab5","modified":1643040240789},{"_id":"source/_posts/Stochastic Calculus.md","hash":"ff8c2405f9168d33589c3f070068fea831a3e5bb","modified":1645709596413},{"_id":"source/CNAME","hash":"e009148b93285eda3ada361958d32b97dce20350","modified":1642921892000},{"_id":"source/tags/index.md","hash":"9a71390c78a266ba2d8507fd5c2b80fe1e22a326","modified":1642837356591},{"_id":"source/categories/index.md","hash":"9c57f9be2f4a6266aeb3b5064ef3651a68bb39e9","modified":1642837369631},{"_id":"themes/hexo-theme-next-master/.gitignore","hash":"56f3470755c20311ddd30d421b377697a6e5e68b","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.editorconfig","hash":"8570735a8d8d034a3a175afd1dd40b39140b3e6a","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.gitattributes","hash":"a54f902957d49356376b59287b894b1a3d7a003f","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.travis.yml","hash":"ecca3b919a5b15886e3eca58aa84aafc395590da","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/LICENSE.md","hash":"18144d8ed58c75af66cb419d54f3f63374cd5c5b","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.stylintrc","hash":"2cf4d637b56d8eb423f59656a11f6403aa90f550","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/package.json","hash":"62fad6de02adbbba9fb096cbe2dcc15fe25f2435","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.eslintrc.json","hash":"cc5f297f0322672fe3f684f823bc4659e4a54c41","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/README.md","hash":"9b4b7d66aca47f9c65d6321b14eef48d95c4dff1","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/crowdin.yml","hash":"e026078448c77dcdd9ef50256bb6635a8f83dca6","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.github/CODE_OF_CONDUCT.md","hash":"aa4cb7aff595ca628cb58160ee1eee117989ec4e","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.github/CONTRIBUTING.md","hash":"e554931b98f251fd49ff1d2443006d9ea2c20461","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/_config.yml","hash":"7b05719105b9e558675ade608c1fcb79ff2695f2","modified":1643989494808},{"_id":"themes/hexo-theme-next-master/gulpfile.js","hash":"1b4fc262b89948937b9e3794de812a7c1f2f3592","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.github/issue-close-app.yml","hash":"7cba457eec47dbfcfd4086acd1c69eaafca2f0cd","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.github/issue_label_bot.yaml","hash":"fca600ddef6f80c5e61aeed21722d191e5606e5b","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.github/PULL_REQUEST_TEMPLATE.md","hash":"1a435c20ae8fa183d49bbf96ac956f7c6c25c8af","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.github/config.yml","hash":"1d3f4e8794986817c0fead095c74f756d45f91ed","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.github/lock.yml","hash":"61173b9522ebac13db2c544e138808295624f7fd","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.github/mergeable.yml","hash":"0ee56e23bbc71e1e76427d2bd255a9879bd36e22","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.github/release-drafter.yml","hash":"3cc10ce75ecc03a5ce86b00363e2a17eb65d15ea","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.github/stale.yml","hash":"fdf82de9284f8bc8e0b0712b4cc1cb081a94de59","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.github/support.yml","hash":"d75db6ffa7b4ca3b865a925f9de9aef3fc51925c","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/AUTHORS.md","hash":"10135a2f78ac40e9f46b3add3e360c025400752f","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/AGPL3.md","hash":"0d2b8c5fa8a614723be0767cc3bca39c49578036","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/ALGOLIA-SEARCH.md","hash":"c7a994b9542040317d8f99affa1405c143a94a38","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/LEANCLOUD-COUNTER-SECURITY.md","hash":"94dc3404ccb0e5f663af2aa883c1af1d6eae553d","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/INSTALLATION.md","hash":"af88bcce035780aaa061261ed9d0d6c697678618","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/DATA-FILES.md","hash":"cddbdc91ee9e65c37a50bec12194f93d36161616","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/LICENSE.txt","hash":"368bf2c29d70f27d8726dd914f1b3211cae4bbab","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/UPDATE-FROM-5.1.X.md","hash":"8b6e4b2c9cfcb969833092bdeaed78534082e3e6","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/MATH.md","hash":"d645b025ec7fb9fbf799b9bb76af33b9f5b9ed93","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/ar.yml","hash":"9815e84e53d750c8bcbd9193c2d44d8d910e3444","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/de.yml","hash":"74c59f2744217003b717b59d96e275b54635abf5","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/default.yml","hash":"45bc5118828bdc72dcaa25282cd367c8622758cb","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/es.yml","hash":"c64cf05f356096f1464b4b1439da3c6c9b941062","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/fa.yml","hash":"3676b32fda37e122f3c1a655085a1868fb6ad66b","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/en.yml","hash":"45bc5118828bdc72dcaa25282cd367c8622758cb","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/fr.yml","hash":"752bf309f46a2cd43890b82300b342d7218d625f","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/hu.yml","hash":"b1ebb77a5fd101195b79f94de293bcf9001d996f","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/ja.yml","hash":"0cf0baa663d530f22ff380a051881216d6adcdd8","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/it.yml","hash":"44759f779ce9c260b895532de1d209ad4bd144bf","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/id.yml","hash":"572ed855d47aafe26f58c73b1394530754881ec2","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/ko.yml","hash":"0feea9e43cd399f3610b94d755a39fff1d371e97","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/tr.yml","hash":"2b041eeb8bd096f549464f191cfc1ea0181daca4","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/ru.yml","hash":"e993d5ca072f7f6887e30fc0c19b4da791ca7a88","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/pt-BR.yml","hash":"67555b1ba31a0242b12fc6ce3add28531160e35b","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/nl.yml","hash":"5af3473d9f22897204afabc08bb984b247493330","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/pt.yml","hash":"718d131f42f214842337776e1eaddd1e9a584054","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/vi.yml","hash":"93393b01df148dcbf0863f6eee8e404e2d94ef9e","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/uk.yml","hash":"3a6d635b1035423b22fc86d9455dba9003724de9","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/zh-HK.yml","hash":"3789f94010f948e9f23e21235ef422a191753c65","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/zh-TW.yml","hash":"8c09da7c4ec3fca2c6ee897b2eea260596a2baa1","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/languages/zh-CN.yml","hash":"a1f15571ee7e1e84e3cc0985c3ec4ba1a113f6f8","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_layout.swig","hash":"6a6e92a4664cdb981890a27ac11fd057f44de1d5","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/page.swig","hash":"db581bdeac5c75fabb0f17d7c5e746e47f2a9168","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/post.swig","hash":"2f6d992ced7e067521fdce05ffe4fd75481f41c5","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/renderer.js","hash":"49a65df2028a1bc24814dc72fa50d52231ca4f05","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/archive.swig","hash":"e4e31317a8df68f23156cfc49e9b1aa9a12ad2ed","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/index.swig","hash":"7f403a18a68e6d662ae3e154b2c1d3bbe0801a23","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/category.swig","hash":"1bde61cf4d2d171647311a0ac2c5c7933f6a53b0","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/tag.swig","hash":"0dfb653bd5de980426d55a0606d1ab122bd8c017","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.github/ISSUE_TEMPLATE/other.md","hash":"d3efc0df0275c98440e69476f733097916a2d579","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.github/ISSUE_TEMPLATE/bug-report.md","hash":"c3e6b8196c983c40fd140bdeca012d03e6e86967","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.github/ISSUE_TEMPLATE/feature-request.md","hash":"12d99fb8b62bd9e34d9672f306c9ae4ace7e053e","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/.github/ISSUE_TEMPLATE/question.md","hash":"53df7d537e26aaf062d70d86835c5fd8f81412f3","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/ru/README.md","hash":"85dd68ed1250897a8e4a444a53a68c1d49eb7e11","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/ru/DATA-FILES.md","hash":"0bd2d696f62a997a11a7d84fec0130122234174e","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/ru/INSTALLATION.md","hash":"9c4fe2873123bf9ceacab5c50d17d8a0f1baef27","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/ru/UPDATE-FROM-5.1.X.md","hash":"5237a368ab99123749d724b6c379415f2c142a96","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/zh-CN/ALGOLIA-SEARCH.md","hash":"34b88784ec120dfdc20fa82aadeb5f64ef614d14","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/zh-CN/CODE_OF_CONDUCT.md","hash":"fb23b85db6f7d8279d73ae1f41631f92f64fc864","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/zh-CN/INSTALLATION.md","hash":"579c7bd8341873fb8be4732476d412814f1a3df7","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/zh-CN/LEANCLOUD-COUNTER-SECURITY.md","hash":"8b18f84503a361fc712b0fe4d4568e2f086ca97d","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/zh-CN/CONTRIBUTING.md","hash":"d3f03be036b75dc71cf3c366cd75aee7c127c874","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/zh-CN/DATA-FILES.md","hash":"ca1030efdfca5e20f9db2e7a428998e66a24c0d0","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/zh-CN/MATH.md","hash":"b92585d251f1f9ebe401abb5d932cb920f9b8b10","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/zh-CN/README.md","hash":"c038629ff8f3f24e8593c4c8ecf0bef3a35c750d","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/docs/zh-CN/UPDATE-FROM-5.1.X.md","hash":"d9ce7331c1236bbe0a551d56cef2405e47e65325","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_macro/post-collapse.swig","hash":"9c8dc0b8170679cdc1ee9ee8dbcbaebf3f42897b","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_macro/post.swig","hash":"090b5a9b6fca8e968178004cbd6cff205b7eba57","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_macro/sidebar.swig","hash":"71655ca21907e9061b6e8ac52d0d8fbf54d0062b","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/footer.swig","hash":"4369b313cbbeae742cb35f86d23d99d4285f7359","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/comments.swig","hash":"db6ab5421b5f4b7cb32ac73ad0e053fdf065f83e","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/widgets.swig","hash":"83a40ce83dfd5cada417444fb2d6f5470aae6bb0","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/pagination.swig","hash":"9876dbfc15713c7a47d4bcaa301f4757bd978269","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/languages.swig","hash":"ba9e272f1065b8f0e8848648caa7dea3f02c6be1","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_scripts/index.swig","hash":"cea942b450bcb0f352da78d76dc6d6f1d23d5029","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_scripts/pjax.swig","hash":"4d2c93c66e069852bb0e3ea2e268d213d07bfa3f","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_scripts/noscript.swig","hash":"d1f2bfde6f1da51a2b35a7ab9e7e8eb6eefd1c6b","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_scripts/three.swig","hash":"a4f42f2301866bd25a784a2281069d8b66836d0b","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/index.swig","hash":"70c3c01dd181de81270c57f3d99b6d8f4c723404","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/baidu-push.swig","hash":"b782eb2e34c0c15440837040b5d65b093ab6ec04","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/quicklink.swig","hash":"311e5eceec9e949f1ea8d623b083cec0b8700ff2","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/events/index.js","hash":"5743cde07f3d2aa11532a168a652e52ec28514fd","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/filters/default-injects.js","hash":"aec50ed57b9d5d3faf2db3c88374f107203617e0","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/filters/front-matter.js","hash":"703bdd142a671b4b67d3d9dfb4a19d1dd7e7e8f7","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/filters/locals.js","hash":"b193a936ee63451f09f8886343dcfdca577c0141","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_scripts/vendors.swig","hash":"ef38c213679e7b6d2a4116f56c9e55d678446069","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/filters/minify.js","hash":"19985723b9f677ff775f3b17dcebf314819a76ac","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/helpers/engine.js","hash":"bdb424c3cc0d145bd0c6015bb1d2443c8a9c6cda","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/helpers/font.js","hash":"40cf00e9f2b7aa6e5f33d412e03ed10304b15fd7","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/filters/post.js","hash":"44ba9b1c0bdda57590b53141306bb90adf0678db","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/helpers/next-config.js","hash":"5e11f30ddb5093a88a687446617a46b048fa02e5","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/rating.swig","hash":"2731e262a6b88eaee2a3ca61e6a3583a7f594702","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/helpers/next-url.js","hash":"958e86b2bd24e4fdfcbf9ce73e998efe3491a71f","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/tags/button.js","hash":"8c6b45f36e324820c919a822674703769e6da32c","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/tags/caniuse.js","hash":"94e0bbc7999b359baa42fa3731bdcf89c79ae2b3","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/tags/center-quote.js","hash":"f1826ade2d135e2f60e2d95cb035383685b3370c","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/tags/group-pictures.js","hash":"d902fd313e8d35c3cc36f237607c2a0536c9edf1","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/tags/label.js","hash":"fc5b267d903facb7a35001792db28b801cccb1f8","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/tags/pdf.js","hash":"8c613b39e7bff735473e35244b5629d02ee20618","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/tags/tabs.js","hash":"93d8a734a3035c1d3f04933167b500517557ba3e","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/tags/mermaid.js","hash":"983c6c4adea86160ecc0ba2204bc312aa338121d","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/tags/note.js","hash":"0a02bb4c15aec41f6d5f1271cdb5c65889e265d9","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/tags/video.js","hash":"e5ff4c44faee604dd3ea9db6b222828c4750c227","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_colors.styl","hash":"a8442520f719d3d7a19811cb3b85bcfd4a596e1f","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/images/algolia_logo.svg","hash":"ec119560b382b2624e00144ae01c137186e91621","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_mixins.styl","hash":"e31a557f8879c2f4d8d5567ee1800b3e03f91f6e","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/main.styl","hash":"a3a3bbb5a973052f0186b3523911cb2539ff7b88","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/images/apple-touch-icon-next.png","hash":"2959dbc97f31c80283e67104fe0854e2369e40aa","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/images/avatar.gif","hash":"18c53e15eb0c84b139995f9334ed8522b40aeaf6","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/images/cc-by-nc.svg","hash":"8d39b39d88f8501c0d27f8df9aae47136ebc59b7","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/images/cc-by-nc-sa.svg","hash":"3031be41e8753c70508aa88e84ed8f4f653f157e","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/images/cc-by-nd.svg","hash":"c563508ce9ced1e66948024ba1153400ac0e0621","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/images/cc-by-nc-nd.svg","hash":"c6524ece3f8039a5f612feaf865d21ec8a794564","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/images/cc-by-sa.svg","hash":"aa4742d733c8af8d38d4c183b8adbdcab045872e","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/images/cc-by.svg","hash":"28a0a4fe355a974a5e42f68031652b76798d4f7e","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/images/favicon-16x16-next.png","hash":"943a0d67a9cdf8c198109b28f9dbd42f761d11c3","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/images/cc-zero.svg","hash":"87669bf8ac268a91d027a0a4802c92a1473e9030","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/js/algolia-search.js","hash":"498d233eb5c7af6940baf94c1a1c36fdf1dd2636","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/images/logo.svg","hash":"d29cacbae1bdc4bbccb542107ee0524fe55ad6de","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/images/favicon-32x32-next.png","hash":"0749d7b24b0d2fae1c8eb7f671ad4646ee1894b1","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/js/bookmark.js","hash":"9734ebcb9b83489686f5c2da67dc9e6157e988ad","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/js/local-search.js","hash":"35ccf100d8f9c0fd6bfbb7fa88c2a76c42a69110","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/js/next-boot.js","hash":"a1b0636423009d4a4e4cea97bcbf1842bfab582c","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/js/motion.js","hash":"72df86f6dfa29cce22abeff9d814c9dddfcf13a9","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/js/utils.js","hash":"730cca7f164eaf258661a61ff3f769851ff1e5da","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/head/head-unique.swig","hash":"000bad572d76ee95d9c0a78f9ccdc8d97cc7d4b4","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/page/page-header.swig","hash":"9b7a66791d7822c52117fe167612265356512477","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/lib/anime.min.js","hash":"47cb482a8a488620a793d50ba8f6752324b46af3","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/page/breadcrumb.swig","hash":"c851717497ca64789f2176c9ecd1dedab237b752","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/post/post-copyright.swig","hash":"954ad71536b6eb08bd1f30ac6e2f5493b69d1c04","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/post/post-followme.swig","hash":"ceba16b9bd3a0c5c8811af7e7e49d0f9dcb2f41e","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/head/head.swig","hash":"810d544019e4a8651b756dd23e5592ee851eda71","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/post/post-related.swig","hash":"f79c44692451db26efce704813f7a8872b7e63a0","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/post/post-reward.swig","hash":"2b1a73556595c37951e39574df5a3f20b2edeaef","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/header/brand.swig","hash":"c70f8e71e026e878a4e9d5ab3bbbf9b0b23c240c","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/post/post-footer.swig","hash":"8f14f3f8a1b2998d5114cc56b680fb5c419a6b07","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/header/index.swig","hash":"7dbe93b8297b746afb89700b4d29289556e85267","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/header/menu-item.swig","hash":"9440d8a3a181698b80e1fa47f5104f4565d8cdf3","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/header/menu.swig","hash":"d31f896680a6c2f2c3f5128b4d4dd46c87ce2130","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/header/sub-menu.swig","hash":"ae2261bea836581918a1c2b0d1028a78718434e0","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/search/algolia-search.swig","hash":"48430bd03b8f19c9b8cdb2642005ed67d56c6e0b","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/search/index.swig","hash":"2be50f9bfb1c56b85b3b6910a7df27f51143632c","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_scripts/pages/schedule.swig","hash":"077b5d66f6309f2e7dcf08645058ff2e03143e6c","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/search/localsearch.swig","hash":"f48a6a8eba04eb962470ce76dd731e13074d4c45","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_scripts/schemes/gemini.swig","hash":"1c910fc066c06d5fbbe9f2b0c47447539e029af7","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_partials/sidebar/site-overview.swig","hash":"c46849e0af8f8fb78baccd40d2af14df04a074af","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_scripts/schemes/muse.swig","hash":"7f14ef43d9e82bc1efc204c5adf0b1dbfc919a9f","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_scripts/schemes/mist.swig","hash":"7f14ef43d9e82bc1efc204c5adf0b1dbfc919a9f","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_scripts/schemes/pisces.swig","hash":"1c910fc066c06d5fbbe9f2b0c47447539e029af7","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/analytics/baidu-analytics.swig","hash":"4790058691b7d36cf6d2d6b4e93795a7b8d608ad","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/analytics/google-analytics.swig","hash":"2fa2b51d56bfac6a1ea76d651c93b9c20b01c09b","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/analytics/growingio.swig","hash":"5adea065641e8c55994dd2328ddae53215604928","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/chat/chatra.swig","hash":"f910618292c63871ca2e6c6e66c491f344fa7b1f","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/chat/tidio.swig","hash":"cba0e6e0fad08568a9e74ba9a5bee5341cfc04c1","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/analytics/index.swig","hash":"1472cabb0181f60a6a0b7fec8899a4d03dfb2040","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/comments/changyan.swig","hash":"f39a5bf3ce9ee9adad282501235e0c588e4356ec","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/comments/gitalk.swig","hash":"d6ceb70648555338a80ae5724b778c8c58d7060d","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/comments/disqus.swig","hash":"b14908644225d78c864cd0a9b60c52407de56183","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/comments/disqusjs.swig","hash":"82f5b6822aa5ec958aa987b101ef860494c6cf1f","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/comments/livere.swig","hash":"f7a9eca599a682479e8ca863db59be7c9c7508c8","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/comments/valine.swig","hash":"be0a8eccf1f6dc21154af297fc79555343031277","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/math/katex.swig","hash":"4791c977a730f29c846efcf6c9c15131b9400ead","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/math/index.swig","hash":"6c5976621efd5db5f7c4c6b4f11bc79d6554885f","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/search/algolia-search.swig","hash":"d35a999d67f4c302f76fdf13744ceef3c6506481","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/math/mathjax.swig","hash":"ecf751321e799f0fb3bf94d049e535130e2547aa","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/search/swiftype.swig","hash":"ba0dbc06b9d244073a1c681ff7a722dcbf920b51","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/search/localsearch.swig","hash":"767b6c714c22588bcd26ba70b0fc19b6810cbacd","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/statistics/cnzz-analytics.swig","hash":"a17ace37876822327a2f9306a472974442c9005d","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/statistics/firestore.swig","hash":"b26ac2bfbe91dd88267f8b96aee6bb222b265b7a","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/statistics/busuanzi-counter.swig","hash":"4b1986e43d6abce13450d2b41a736dd6a5620a10","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/statistics/index.swig","hash":"5f6a966c509680dbfa70433f9d658cee59c304d7","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/statistics/lean-analytics.swig","hash":"d56d5af427cdfecc33a0f62ee62c056b4e33d095","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/events/lib/config.js","hash":"d34c6040b13649714939f59be5175e137de65ede","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/tags/mermaid.swig","hash":"f3c43664a071ff3c0b28bd7e59b5523446829576","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/events/lib/injects-point.js","hash":"6661c1c91c7cbdefc6a5e6a034b443b8811235a1","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/events/lib/injects.js","hash":"f233d8d0103ae7f9b861344aa65c1a3c1de8a845","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/filters/comment/changyan.js","hash":"a54708fd9309b4357c423a3730eb67f395344a5e","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/filters/comment/default-config.js","hash":"7f2d93af012c1e14b8596fecbfc7febb43d9b7f5","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/filters/comment/common.js","hash":"2486f3e0150c753e5f3af1a3665d074704b8ee2c","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/layout/_third-party/tags/pdf.swig","hash":"d30b0e255a8092043bac46441243f943ed6fb09b","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/filters/comment/disqus.js","hash":"4c0c99c7e0f00849003dfce02a131104fb671137","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/filters/comment/gitalk.js","hash":"e51dc3072c1ba0ea3008f09ecae8b46242ec6021","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/filters/comment/disqusjs.js","hash":"7f8b92913d21070b489457fa5ed996d2a55f2c32","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/filters/comment/livere.js","hash":"d5fefc31fba4ab0188305b1af1feb61da49fdeb0","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/scripts/filters/comment/valine.js","hash":"6cbd85f9433c06bae22225ccf75ac55e04f2d106","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_variables/Gemini.styl","hash":"f4e694e5db81e57442c7e34505a416d818b3044a","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_variables/Pisces.styl","hash":"612ec843372dae709acb17112c1145a53450cc59","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_variables/base.styl","hash":"818508748b7a62e02035e87fe58e75b603ed56dc","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_variables/Muse.styl","hash":"62df49459d552bbf73841753da8011a1f5e875c8","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_variables/Mist.styl","hash":"f70be8e229da7e1715c11dd0e975a2e71e453ac8","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/js/schemes/pisces.js","hash":"0ac5ce155bc58c972fe21c4c447f85e6f8755c62","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/js/schemes/muse.js","hash":"1eb9b88103ddcf8827b1a7cbc56471a9c5592d53","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/back-to-top.styl","hash":"a47725574e1bee3bc3b63b0ff2039cc982b17eff","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/back-to-top-sidebar.styl","hash":"ca5e70662dcfb261c25191cc5db5084dcf661c76","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/lib/velocity/velocity.min.js","hash":"2f1afadc12e4cf59ef3b405308d21baa97e739c6","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/mobile.styl","hash":"681d33e3bc85bdca407d93b134c089264837378c","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/lib/velocity/velocity.ui.min.js","hash":"ed5e534cd680a25d8d14429af824f38a2c7d9908","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/outline.styl","hash":"a1690e035b505d28bdef2b4424c13fc6312ab049","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/reading-progress.styl","hash":"2e3bf7baf383c9073ec5e67f157d3cb3823c0957","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/base.styl","hash":"0b2c4b78eead410020d7c4ded59c75592a648df8","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/buttons.styl","hash":"a2e9e00962e43e98ec2614d6d248ef1773bb9b78","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/pagination.styl","hash":"8f58570a1bbc34c4989a47a1b7d42a8030f38b06","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/scaffolding.styl","hash":"523fb7b653b87ae37fc91fc8813e4ffad87b0d7e","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/normalize.styl","hash":"b56367ea676ea8e8783ea89cd4ab150c7da7a060","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/components.styl","hash":"8e7b57a72e757cf95278239641726bb2d5b869d1","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/comments.styl","hash":"b1f0fab7344a20ed6748b04065b141ad423cf4d9","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/tables.styl","hash":"18ce72d90459c9aa66910ac64eae115f2dde3767","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/toggles.styl","hash":"179e33b8ac7f4d8a8e76736a7e4f965fe9ab8b42","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_schemes/Mist/_header.styl","hash":"f6516d0f7d89dc7b6c6e143a5af54b926f585d82","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_schemes/Gemini/index.styl","hash":"7785bd756e0c4acede3a47fec1ed7b55988385a5","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_schemes/Mist/_layout.styl","hash":"bb7ace23345364eb14983e860a7172e1683a4c94","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_schemes/Mist/_posts-expand.styl","hash":"6136da4bbb7e70cec99f5c7ae8c7e74f5e7c261a","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_schemes/Mist/_menu.styl","hash":"7104b9cef90ca3b140d7a7afcf15540a250218fc","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_schemes/Muse/_layout.styl","hash":"4d1c17345d2d39ef7698f7acf82dfc0f59308c34","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_schemes/Mist/index.styl","hash":"a717969829fa6ef88225095737df3f8ee86c286b","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_schemes/Muse/_header.styl","hash":"f0131db6275ceaecae7e1a6a3798b8f89f6c850d","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_schemes/Muse/_sub-menu.styl","hash":"c48ccd8d6651fe1a01faff8f01179456d39ba9b1","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_schemes/Muse/_sidebar.styl","hash":"2b2e7b5cea7783c9c8bb92655e26a67c266886f0","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_schemes/Muse/index.styl","hash":"6ad168288b213cec357e9b5a97674ff2ef3a910c","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_schemes/Muse/_menu.styl","hash":"93db5dafe9294542a6b5f647643cb9deaced8e06","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_schemes/Pisces/_header.styl","hash":"e282df938bd029f391c466168d0e68389978f120","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_schemes/Pisces/_menu.styl","hash":"85da2f3006f4bef9a2199416ecfab4d288f848c4","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_schemes/Pisces/_sidebar.styl","hash":"44f47c88c06d89d06f220f102649057118715828","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_schemes/Pisces/_sub-menu.styl","hash":"e740deadcfc4f29c5cb01e40f9df6277262ba4e3","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_schemes/Pisces/index.styl","hash":"6ad168288b213cec357e9b5a97674ff2ef3a910c","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_schemes/Pisces/_layout.styl","hash":"70a4324b70501132855b5e59029acfc5d3da1ebd","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/lib/font-awesome/css/all.min.css","hash":"0038dc97c79451578b7bd48af60ba62282b4082b","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/pages/breadcrumb.styl","hash":"fafc96c86926b22afba8bb9418c05e6afbc05a57","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/pages/categories.styl","hash":"2bd0eb1512415325653b26d62a4463e6de83c5ac","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/lib/font-awesome/webfonts/fa-regular-400.woff2","hash":"260bb01acd44d88dcb7f501a238ab968f86bef9e","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/pages/pages.styl","hash":"7504dbc5c70262b048143b2c37d2b5aa2809afa2","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/pages/tag-cloud.styl","hash":"d21d4ac1982c13d02f125a67c065412085a92ff2","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/pages/schedule.styl","hash":"e771dcb0b4673e063c0f3e2d73e7336ac05bcd57","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/post/post-eof.styl","hash":"902569a9dea90548bec21a823dd3efd94ff7c133","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/post/post-gallery.styl","hash":"72d495a88f7d6515af425c12cbc67308a57d88ea","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/post/post-collapse.styl","hash":"e75693f33dbc92afc55489438267869ae2f3db54","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/post/post-copyright.styl","hash":"f49ca072b5a800f735e8f01fc3518f885951dd8e","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/post/post-followme.styl","hash":"1e4190c10c9e0c9ce92653b0dbcec21754b0b69d","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/post/post-expand.styl","hash":"ded41fd9d20a5e8db66aaff7cc50f105f5ef2952","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/post/post-reward.styl","hash":"d114b2a531129e739a27ba6271cfe6857aa9a865","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/post/post-rtl.styl","hash":"f5c2788a78790aca1a2f37f7149d6058afb539e0","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/post/post-nav.styl","hash":"6a97bcfa635d637dc59005be3b931109e0d1ead5","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/post/post-header.styl","hash":"65cb6edb69e94e70e3291e9132408361148d41d5","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/post/post-tags.styl","hash":"99e12c9ce3d14d4837e3d3f12fc867ba9c565317","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/post/post-widgets.styl","hash":"5b5649b9749e3fd8b63aef22ceeece0a6e1df605","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/post/post.styl","hash":"a760ee83ba6216871a9f14c5e56dc9bd0d9e2103","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/third-party/math.styl","hash":"b49e9fbd3c182b8fc066b8c2caf248e3eb748619","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/third-party/related-posts.styl","hash":"e2992846b39bf3857b5104675af02ba73e72eed5","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/third-party/search.styl","hash":"9f0b93d109c9aec79450c8a0cf4a4eab717d674d","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/third-party/third-party.styl","hash":"9a878d0119785a2316f42aebcceaa05a120b9a7a","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/components/third-party/gitalk.styl","hash":"8a7fc03a568b95be8d3337195e38bc7ec5ba2b23","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/header/bookmark.styl","hash":"e2d606f1ac343e9be4f15dbbaf3464bc4df8bf81","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/header/github-banner.styl","hash":"e7a9fdb6478b8674b1cdf94de4f8052843fb71d9","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/header/headerband.styl","hash":"0caf32492692ba8e854da43697a2ec8a41612194","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/header/header.styl","hash":"a793cfff86ad4af818faef04c18013077873f8f0","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/header/site-nav.styl","hash":"b2fc519828fe89a1f8f03ff7b809ad68cd46f3d7","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/header/menu.styl","hash":"5f432a6ed9ca80a413c68b00e93d4a411abf280a","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/header/site-meta.styl","hash":"45a239edca44acecf971d99b04f30a1aafbf6906","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/sidebar/sidebar-author-links.styl","hash":"2cb1876e9e0c9ac32160888af27b1178dbcb0616","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/footer/footer.styl","hash":"454a4aebfabb4469b92a8cbb49f46c49ac9bf165","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/sidebar/sidebar-author.styl","hash":"fa0222197b5eee47e18ac864cdc6eac75678b8fe","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/sidebar/sidebar-blogroll.styl","hash":"44487d9ab290dc97871fa8dd4487016deb56e123","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/sidebar/sidebar-button.styl","hash":"1f0e7fbe80956f47087c2458ea880acf7a83078b","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/sidebar/sidebar-dimmer.styl","hash":"9b479c2f9a9bfed77885e5093b8245cc5d768ec7","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/sidebar/sidebar-toggle.styl","hash":"b3220db827e1adbca7880c2bb23e78fa7cbe95cb","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/sidebar/sidebar.styl","hash":"a9cd93c36bae5af9223e7804963096274e8a4f03","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/sidebar/sidebar-nav.styl","hash":"a960a2dd587b15d3b3fe1b59525d6fa971c6a6ec","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/sidebar/sidebar-toc.styl","hash":"a05a4031e799bc864a4536f9ef61fe643cd421af","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/outline/sidebar/site-state.styl","hash":"2a47f8a6bb589c2fb635e6c1e4a2563c7f63c407","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/highlight/copy-code.styl","hash":"f71a3e86c05ea668b008cf05a81f67d92b6d65e4","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/highlight/theme.styl","hash":"3b3acc5caa0b95a2598bef4eeacb21bab21bea56","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/highlight/diff.styl","hash":"d3f73688bb7423e3ab0de1efdf6db46db5e34f80","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/highlight/highlight.styl","hash":"35c871a809afa8306c8cde13651010e282548bc6","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/tags/blockquote-center.styl","hash":"1d2778ca5aeeeafaa690dc2766b01b352ab76a02","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/tags/group-pictures.styl","hash":"709d10f763e357e1472d6471f8be384ec9e2d983","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/tags/pdf.styl","hash":"b49c64f8e9a6ca1c45c0ba98febf1974fdd03616","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/tags/note.styl","hash":"e4d9a77ffe98e851c1202676940097ba28253313","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/tags/label.styl","hash":"d7fce4b51b5f4b7c31d93a9edb6c6ce740aa0d6b","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/tags/tags.styl","hash":"9e4c0653cfd3cc6908fa0d97581bcf80861fb1e7","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/css/_common/scaffolding/tags/tabs.styl","hash":"f23670f1d8e749f3e83766d446790d8fd9620278","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/lib/font-awesome/webfonts/fa-brands-400.woff2","hash":"509988477da79c146cb93fb728405f18e923c2de","modified":1627554806000},{"_id":"themes/hexo-theme-next-master/source/lib/font-awesome/webfonts/fa-solid-900.woff2","hash":"75a88815c47a249eadb5f0edc1675957f860cca7","modified":1627554806000},{"_id":"public/categories/index.html","hash":"cff5d8ae9ab2876324f31c6b90d0bcb51928fe9a","modified":1686245102652},{"_id":"public/tags/index.html","hash":"a6b3394fd5087087b1f6d6166ab7688ca7061257","modified":1686245102652},{"_id":"public/categories/学习笔记/index.html","hash":"763f7f2023b819b0a9020a72487e44e6c842750c","modified":1686245102652},{"_id":"public/archives/index.html","hash":"dcb739993119ab23ab6d06be11f4fcdf546a2baa","modified":1686245102652},{"_id":"public/archives/2022/index.html","hash":"979beec77f92c99b5ff3a964d58f92289fd8caa9","modified":1686245102652},{"_id":"public/archives/2022/01/index.html","hash":"a659ca04d1dc334d29bc58483d9a92056941f31d","modified":1686245102652},{"_id":"public/tags/金融/index.html","hash":"0099b3ec6c42cf084bdc6bb93e6df3c55a9c8874","modified":1686245102652},{"_id":"public/tags/数学/index.html","hash":"0154279b97965603e12afa8503d8846e14550542","modified":1686245102652},{"_id":"public/2022/01/25/Stochastic Calculus/index.html","hash":"f5fa4e3b06d28f4c3eabd4a3528694578b3a0567","modified":1686245102652},{"_id":"public/index.html","hash":"9cf248cd9bee538c81deffb934f28d59c8fb26c3","modified":1686245102652},{"_id":"public/CNAME","hash":"e009148b93285eda3ada361958d32b97dce20350","modified":1645709615031},{"_id":"public/images/apple-touch-icon-next.png","hash":"2959dbc97f31c80283e67104fe0854e2369e40aa","modified":1645709615031},{"_id":"public/images/algolia_logo.svg","hash":"ec119560b382b2624e00144ae01c137186e91621","modified":1645709615031},{"_id":"public/images/cc-by-nc-nd.svg","hash":"c6524ece3f8039a5f612feaf865d21ec8a794564","modified":1645709615031},{"_id":"public/images/cc-by-nc.svg","hash":"8d39b39d88f8501c0d27f8df9aae47136ebc59b7","modified":1645709615031},{"_id":"public/images/cc-by-nc-sa.svg","hash":"3031be41e8753c70508aa88e84ed8f4f653f157e","modified":1645709615031},{"_id":"public/images/avatar.gif","hash":"18c53e15eb0c84b139995f9334ed8522b40aeaf6","modified":1645709615031},{"_id":"public/images/cc-by-nd.svg","hash":"c563508ce9ced1e66948024ba1153400ac0e0621","modified":1645709615031},{"_id":"public/images/cc-by-sa.svg","hash":"aa4742d733c8af8d38d4c183b8adbdcab045872e","modified":1645709615031},{"_id":"public/images/favicon-16x16-next.png","hash":"943a0d67a9cdf8c198109b28f9dbd42f761d11c3","modified":1645709615031},{"_id":"public/images/cc-by.svg","hash":"28a0a4fe355a974a5e42f68031652b76798d4f7e","modified":1645709615031},{"_id":"public/images/cc-zero.svg","hash":"87669bf8ac268a91d027a0a4802c92a1473e9030","modified":1645709615031},{"_id":"public/images/logo.svg","hash":"d29cacbae1bdc4bbccb542107ee0524fe55ad6de","modified":1645709615031},{"_id":"public/lib/font-awesome/webfonts/fa-regular-400.woff2","hash":"260bb01acd44d88dcb7f501a238ab968f86bef9e","modified":1645709615031},{"_id":"public/images/favicon-32x32-next.png","hash":"0749d7b24b0d2fae1c8eb7f671ad4646ee1894b1","modified":1645709615031},{"_id":"public/js/bookmark.js","hash":"9734ebcb9b83489686f5c2da67dc9e6157e988ad","modified":1645709615031},{"_id":"public/js/algolia-search.js","hash":"498d233eb5c7af6940baf94c1a1c36fdf1dd2636","modified":1645709615031},{"_id":"public/js/local-search.js","hash":"35ccf100d8f9c0fd6bfbb7fa88c2a76c42a69110","modified":1645709615031},{"_id":"public/js/motion.js","hash":"72df86f6dfa29cce22abeff9d814c9dddfcf13a9","modified":1645709615031},{"_id":"public/js/utils.js","hash":"730cca7f164eaf258661a61ff3f769851ff1e5da","modified":1645709615031},{"_id":"public/js/next-boot.js","hash":"a1b0636423009d4a4e4cea97bcbf1842bfab582c","modified":1645709615031},{"_id":"public/js/schemes/pisces.js","hash":"0ac5ce155bc58c972fe21c4c447f85e6f8755c62","modified":1645709615031},{"_id":"public/js/schemes/muse.js","hash":"1eb9b88103ddcf8827b1a7cbc56471a9c5592d53","modified":1645709615031},{"_id":"public/lib/velocity/velocity.ui.min.js","hash":"ed5e534cd680a25d8d14429af824f38a2c7d9908","modified":1645709615031},{"_id":"public/css/main.css","hash":"306e97152dd12f9f33747a6869932924229450a1","modified":1645709615031},{"_id":"public/lib/anime.min.js","hash":"47cb482a8a488620a793d50ba8f6752324b46af3","modified":1645709615031},{"_id":"public/lib/velocity/velocity.min.js","hash":"2f1afadc12e4cf59ef3b405308d21baa97e739c6","modified":1645709615031},{"_id":"public/lib/font-awesome/css/all.min.css","hash":"0038dc97c79451578b7bd48af60ba62282b4082b","modified":1645709615031},{"_id":"public/lib/font-awesome/webfonts/fa-brands-400.woff2","hash":"509988477da79c146cb93fb728405f18e923c2de","modified":1645709615031},{"_id":"public/lib/font-awesome/webfonts/fa-solid-900.woff2","hash":"75a88815c47a249eadb5f0edc1675957f860cca7","modified":1645709615031},{"_id":"source/_posts/Managing cash-in risk embedded in Portfolio Insurance strategies.md","hash":"6fd658086477ab829ae4237abf0d6408ac6cf84c","modified":1650271849177},{"_id":"source/_posts/OLS method.md","hash":"0cdbc8d9f1c4c15d7012988122c4732a716e99f5","modified":1650355021732},{"_id":"public/2022/04/18/OLS method/index.html","hash":"57077f9a44bf3b37e4ca6e27c354b30df5402e5f","modified":1686245102652},{"_id":"public/archives/2022/04/index.html","hash":"72b7321dd37c4c11ca0aa4ce77d446d5bccfc512","modified":1686245102652},{"_id":"public/tags/经济/index.html","hash":"f53135481dd2a688156e5859871cbb10bf7c1ce3","modified":1686245102652},{"_id":"public/2022/04/18/Managing cash-in risk embedded in Portfolio Insurance strategies/index.html","hash":"613a63b25e1b5b73fcc1700b8073c2bbc23647aa","modified":1686245102652},{"_id":"source/_posts/WebChat.md","hash":"25dfa563f4ea1f10a4d0016aefb7ba1f413b709f","modified":1652212525073},{"_id":"public/archives/2022/05/index.html","hash":"2f4aa2f95c837f3070b5a53d2921861aabc72c92","modified":1686245102652},{"_id":"public/2022/05/11/WebChat/index.html","hash":"9aa9d1cc28ebcffda2d80a4ca41b1f4b47f29dd6","modified":1686245102652},{"_id":"public/categories/个人项目/index.html","hash":"dec18be691a14eb34a617ebdcc60c823a8948f8b","modified":1686245102652},{"_id":"public/tags/计算机/index.html","hash":"2c3c3f55e89f6c01ae4763873967d715a0098d45","modified":1686245102652},{"_id":"source/_posts/Back.md","hash":"d64d1220c803f4ab749cd8eb0a144c950a3880a0","modified":1686245094659},{"_id":"public/2023/06/09/Back/index.html","hash":"809d4c4c1b861a26953e7182fa3905012c3c36d3","modified":1686245102652},{"_id":"public/archives/2023/index.html","hash":"ca326643ea852a9deb0d2c6f56a1bd8f7c9f1592","modified":1686245102652},{"_id":"public/archives/2023/06/index.html","hash":"74e779553fa8dc956525a3b7a5224b99a96ffe02","modified":1686245102652}],"Category":[{"name":"学习笔记","_id":"cl0110i7600039jpk6cbucvk0"},{"name":"个人项目","_id":"cl30kgq3500006fpk8jqgeljk"}],"Data":[],"Page":[{"title":"文章分类","date":"2019-01-14T12:53:04.000Z","type":"categories","_content":"","source":"categories/index.md","raw":"---\ntitle: 文章分类\ndate: 2019-01-14 20:53:04\ntype: \"categories\" #这部分是新添加的\n---\n","updated":"2022-01-22T07:42:49.631Z","path":"categories/index.html","comments":1,"layout":"page","_id":"cl0110i6x00009jpk9kifbzzu","content":"","site":{"data":{}},"excerpt":"","more":""},{"title":"标签","date":"2019-01-14T12:56:48.000Z","type":"tags","_content":"","source":"tags/index.md","raw":"---\ntitle: 标签\ndate: 2019-01-14 20:56:48\ntype: \"tags\" #新添加的内容\n---\n","updated":"2022-01-22T07:42:36.591Z","path":"tags/index.html","comments":1,"layout":"page","_id":"cl0110i7400029jpkgs6g581n","content":"","site":{"data":{}},"excerpt":"","more":""}],"Post":[{"layout":"posts","title":"Stochastic Calculus for Finance","date":"2022-01-24T16:00:00.000Z","_content":"\n<head>\n <script src=\"https://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML\" type=\"text/javascript\"></script>\n <script type=\"text/x-mathjax-config\">\n MathJax.Hub.Config({\n tex2jax: {\n skipTags: ['script', 'noscript', 'style', 'textarea', 'pre'],\n inlineMath: [['$','$']]\n }\n });\n </script>\n</head>\n\n\n# General Probability Theory\n\n## infinite probability spaces\n\n### $\\sigma$-代数\n\n$\\sigma-algebra$, F is a collection of subsets of $\\Omega$\n\n1. empty set belongs to it\n2. whenever a set belongs to it, its complement also belong to F\n3. the union of a sequence of sets in F belongs to F\n\n可以有推论:\n\n1. $\\Omega$ 一定在F中\n2. 集合序列的交集也一定在F中\n\n### 概率测量的定义 probability measure\n\n一个函数,定义域是F中的任意集合,值域是[0,1],满足:\n\n1. $P(\\Omega)=1$\n2. $P(\\cup^\\infty_{n=1} A_n)=\\sum^\\infty_{n=1} P(A_n)$\n \n $triple(\\Omega,F,P)$称为概率空间\n \n\nuniform(Lebesgue)measure on [0,1]:在0,1之间选取一个数,定义:\n\n$P(a,b)=P[a,b]=b-a,0\\le a \\le b\\le 1$\n\n可以用上述方式表述概率的集合的集合构成了sigma代数,从包含的所有闭区间出发,称为Borel sigma代数\n\n$(a,b)=\\cup_{n=1}^\\infty[a+\\frac{1}{n},b-\\frac{1}{n}]$ ,所以sigma代数中包含了所有开区间,分别取补集可以导出包含开区间与闭区间的并,从而导出所有集合 \n\n通过从闭区间出发,添加所有必要元素构成的sigma代数称之为$Borel \\quad\\sigma-algebra$ of subsets of [0,1] and is denoted B[0,1]\n\nevent A occurs almost surely if P(A)=1\n\n## Random variables and distributions\n\ndefinition: a random variable is a real-valued function X defined on $\\Omega$ with the property that for every Borel subset B of **R,** the subset of $\\Omega$ given by:\n\n$$\n\\begin{equation*}\\{x\\in B\\}=\\{\\omega \\in \\Omega ; X(\\omega )\\in B\\}\\end{equation*}\n$$\n\nis in the $\\sigma$-algebra F\n\n本质是把事件映射为实数,同时为了保证可以拟映射,要求函数可测。\n\n构造R的Borel子集?从所有的闭区间出发,闭区间的交——特别地,开区间也包含进来,从而开集包含进来 ,因为每个开集可以写成开区间序列的并。闭集也是Borel集合,因为是开集的补集。\n\n关注X取值包含于某集合而不是具体的值\n\nDefinition: let X be a random variable on a probability space, the distribution measure of X is the probability measure $\\mu _X$that assigns to each Borel subset B of R the mass $\\mu _X(B)=P\\{X\\in B\\}$ \n\nRandom variable 有distribution 但两者不等同,两个不同的Random variable 可以有相同的distribution,一个单独的random variable 可以有两个不同的distribution\n\ncdf:$F(x)=P\\{X\\le x\\}$\n\n$\\mu_X(x,y]=F(y)-F(x)$\n\n## Expectations\n\n$E(X)=\\sum X(\\omega )P(\\omega )$\n\n$\\{\\Omega , F, P\\}$ random variable $X(\\omega )$ P是概率空间中的测度\n\n$A_k=\\{\\omega \\in \\Omega ; y_k\\le X(\\omega ) < y_{k+1}\\}$\n\nlower Lebesgue sum $LS^-_{\\Pi}=\\sum y_k P(A_k)$\n\nthe maximal distance between the $y_k$ partition points approaches zero, we get Lebesgue integral$\\int_{\\Omega}X(\\omega )dP(\\omega)$\n\nLebesgue integral相当于把积分概念拓展到可测空间,而不是单纯的更换了求和方式。横坐标实际上是$\\Omega$的测度。\n\nif the random variables X can take both positive and negative values, we can define the positive and negative parts of X:\n\n$X^+=max\\{X,0\\}$, $X^-=min\\{-X,0\\}$\n\n$\\int XdP=\\int X^+dP-\\int X^- dP$\n\n**Comparison**\n\nIf $X\\le Y$ almost surely, and if the Lebesgue integral are defined, then\n\n$\\int _{\\Omega}X(\\omega)dP(\\omega)\\le \\int _{\\Omega}Y(\\omega)dP(\\omega)$\n\nIf $X=Y$ almost surely, and if the Lebesgue integral are defined, then\n\n$\\int _{\\Omega}X(\\omega)dP(\\omega)=\\int _{\\Omega}Y(\\omega)dP(\\omega)$\n\n**Integrability, Linearity ...**\n\n**Jensen’s inequality**\n\nif $\\phi$ is a convex, real-valued function defined on R and if $E|X|<\\infty$ ,then\n\n$\\phi(EX)\\le E\\phi(X)$\n\n$\\mathcal{B} (\\mathbb{R})$ be the sigma-algebra of Borel subsets of $\\mathbb{R}$, the Lebesgue measure $\\mathcal{L}$ on R assigns to each set $B\\in \\mathcal{B}(\\mathbb{R})$ a number in $[0,\\infty)$ or the value $\\infty$ so that:\n\n1. $\\mathcal{L}[a,b] =b-a$ \n2. if $B_1,B_2,B_3 \\dots$ is a sequence of disjoint sets in $\\mathcal{B}$ ,then we have the countable additivity property: $\\mathcal{L} (\\cup_{n=1}^\\infty B_n)=\\sum_{n=1}^\\infty \\mathcal{L} (B_n)$\n\n黎曼积分有且只有在区间中非连续点的集合的Lebesgue测度为零时有定义,即f在区间上几乎处处连续\n\n若f的Riemann积分在区间上存在,则f是Borel可测的,而且Riemann积分和Lebesgue积分一致。\n\n### convergence of integrals\n\n**definition**\n\n$X_1,X_2,X_3\\dots$ be a sequence of random variables on the same probability space$(\\Omega, \\mathcal{F},\\mathbb{P})$, $X$ be another random variable. $X_1,X_2,X_3\\dots$ converges to $X$ almost surely $lim_{n\\to \\infty}X_n=X$ almost surely. if the set of $\\omega \\in \\Omega$ for the sequence has limit $X(\\omega)$ is a set with probability one. \n\nStrong law of Large Numbers: \n\n实的Borel可测的函数列$f_1,f_2,f_3\\dots$ defined on$\\mathbb{R}$, $f$ 也是实的Borel可测函数,the sequence converges to f almost every-where if 序列极限不为f的点的集合的 Lebesgue measure为零\n\n$lim_{n\\to \\infty}f_n=f \\textit{ almost everywhere}$\n\n当随机变量几乎趋于一致,他们的期望值趋于极限的期望。类似地,当函数几乎处处converge,通常情况下,他们的lebesgue积分收敛到极限的积分。特殊的情况,就是\n\n$lim_{n\\to \\infty}\\int f_n(x)dx\\ne \\int lim_{n\\to \\infty} f_n(x)dx$\n\n例如f是正态分布,左边为1,右边lebesgue积分为0\n\n**theorem** *Monotone convergence* $X_1,X_2,X_3\\dots$ be a sequence of random variables converging almost surely to another random variable $X$ if 序列几乎单调不减,期望的极限是EX\n\n$lim_{n \\to \\infty}\\mathbb{E}X_n=\\mathbb{E} X$\n\n把这里的随机变量换成Borel可测实值函数,也是成立的\n\n$lim_{n\\to \\infty}\\int_{-\\infty}^{\\infty}f_n(x)dx=\\int_{-\\infty}^{\\infty}f(x)dx$\n\n即使随机变量几乎不发散,但期望可能发散\n\n**theorem Dominated convergence** 如果随机变量序列几乎趋于一致于$X$,且满足 $|X_n|\\le Y$ almost surely for every n, $\\mathbb{E}Y<\\infty$, then $lim_{n\\to \\infty}EX_n=EX$\n\n对于Borel可测实值函数也一样成立:若$f_n(x)\\le g$ almost surely for every n, and $\\int_{-\\infty}^\\infty g(x)dx<\\infty$\n\n若$f_n(x)\\le g$ almost surely for every n, and $\\int_{-\\infty}^\\infty g(x)dx<\\infty$\n\n$lim_{n\\to \\infty}\\int_{-\\infty}^\\infty f_n(x)dx=\\int_{-\\infty}^\\infty f(x)dx$\n\n## Computation of Expectations\n\n**theorem** $g$ is a Borel measurable function on $\\mathbb{R}$ Then:\n\n$\\mathbb{E} |g(X)|=\\int_\\mathbb{R} |g(x)|d\\mu_X(x)$ , if this quantity is finite, then$\\mathbb{E} g(X)=\\int_\\mathbb{R} g(x)d\\mu_X(x)$\n\nPROOF\n\n1. $\\mathbb{EI}_B(X)=\\mathbb{P}\\{X\\in B\\}=\\mu_X(B)=\\int_\\mathbb{R}\\mathbb{I}_B(x)d\\mu_X(x)$\n2. nonnegative simple functions. A simple function is a finite sum of indicator functions times constants \n \n $$g(x)=\\sum\\alpha_k \\mathbb{I}_{B_k}(x)$$\n \n so \n \n $$\\mathbb{E}g(X)=\\mathbb{E}\\sum \\alpha_k \\mathbb{I}\\_{B\\_k}(X)=\\sum \\alpha_k\\int_R\\mathbb{I}\\_{B\\_k}d\\mu_X(x)=\\int_R(\\sum \\alpha_k\\mathbb{I}\\_{B\\_k}(x))d\\mu_X(x)=\\int_R g(x)d\\mu_X(x)$$\n \n3. when g is nonnegative Borel-measurable functions. \n \n $$B_{k,n}=\\{x;\\frac{k}{2^n}\\le g(x)\\le \\frac{k+1}{2^n}\\},k=0,1,2,\\dots,4^n-1$$\n \n $$g_n(x)=\\sum \\frac{k}{2^n}\\mathbb{I}\\_{B\\_{k,n}}(x)$$\n \n $$\\mathbb{E}g(X)=\\lim \\mathbb{E}g_n(X)=\\lim \\int_R g_n(x)d\\mu_X(x)=\\int_R g(x)d\\mu_X(x)$$\n \n4. when g is general Borel-measurable function.\n \n $g^+(x)=\\max\\{g(x),0\\},g^-(x)\\min\\{-g(x),0\\}$\n \n\n**Theorem** $X$ is a random variable on a probability space $(\\Omega,\\mathcal{F},\\mathbb{P})$, and let g be a Borel measurable function on $\\mathbb{R}$. $X$ has a density $f$ \n\n$\\mathbb{E}|g(X)|=\\int|g(x)|f(x)dx$\n\nif quantity is finite, then \n\n$\\mathbb{E}g(X)=\\int g(x)f(x)dx$\n\nPROOF\n\nsimple functions\n\n$$\\mathbb{E}g(X)=\\mathbb{E}(\\sum \\alpha_k \\mathbb{I}\\_{B\\_k}(X))=\\sum \\alpha_k \\mathbb{E}\\mathbb{I}\\_{B_k}(X)=\\sum \\alpha_k \\int \\mathbb{I}\\_{B\\_k}f(x)dx\\\\\\\\=\\int \\sum \\alpha\n\\_k\\mathbb{I}\\_{B\\_k}(x)f(x)dx=\\int g(x)f(x)dx$$\n\nnonnegative Borel measurable functions\n\n$$\\mathbb{E}g_n(X)=\\int g_n(x)f(x)dx$$\n\n## Change of Measure\n\nWe can use a positive random variable $Z$ to change probability measures on a space $\\Omega$. We need to do this when we change from the actual probability measure $\\mathbb{P}$ to the risk-neutral probability measure $\\widetilde{\\mathbb{P}}$ in models of financial markets.\n\n$$Z(\\omega)\\mathbb{P}(\\omega)=\\widetilde{\\mathbb{P}}(\\omega)$$\n\nto change from $\\mathbb{P}$ to $\\widetilde{\\mathbb{P}}$, we need to reassign probabilities in $\\Omega$ using $Z$ to tell us where in $\\Omega$ we should revise the probability upward and where downward. \n\n*we should do this set-by-set, but not $\\omega$-by-$\\omega$. According to following theorem*\n\n**Theorem** let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space and let $Z$ be an almost surely nonnegative random variable with $\\mathbb{E}Z=1$. for $A\\in\\mathcal{F}$, define $\\widetilde{\\mathbb{P}}(A)=\\int_AZ(\\omega)d\\mathbb{P}(\\omega)$. Then $\\widetilde{\\mathbb{P}}$ is a probability measure. If $X$ is a nonnegative random variable, then$\\widetilde{\\mathbb{E}}X=\\mathbb{E}[XZ]$. If $Z$ is almost surely strictly positive, we also have $\\mathbb{E}Y=\\widetilde{\\mathbb{E}}[\\frac{Y}{Z}]$ for every nonnegative random variable $Y$.\n\nPROOF\n\n$\\widetilde{\\mathbb{P}}(\\Omega)=1$, and countably additive. \n\ncountably additive\n\nlet $A_1,A_2,A_3,\\dots$ be a sequence of disjoint sets in $\\mathcal{F}$, and define $B_n=\\cup_{k=1}^n A_k$\n\nwe can use the monotone convergence theorem, to write\n\n$$\\widetilde{\\mathbb{P}}(\\cup \\_{k=1}^\\infty A\\_k)=\\widetilde{\\mathbb{P}}(B\\_\\infty)=\\int\\_\\Omega \\mathbb{I}\\_{B\\_\\infty}(\\omega)Z(\\omega)d\\mathbb{P}(\\omega)\\\\\\\\=\\lim\\_{n\\to \\infty}\\int\\_\\Omega \\mathbb{I}\\_{B\\_n}(\\omega)Z(\\omega)d\\mathbb{P}(\\omega)\\\\\\\\=\\lim\\_{n\\to \\infty}\\sum\\int\\_\\Omega\\mathbb{I}\\_{A\\_k}(\\omega)Z(\\omega)d\\mathbb{P}(\\omega)=\\sum\\_{k=1}^\\infty\\widetilde{\\mathbb{P}}(A\\_k)$$\n\n**Definition** 如果两个概率测度下sigma代数中零概率的集合相同,那么称两个概率测度为equivalent\n\n在金融中,实际概率测度和风险中性概率测度就是equivalent的,在risk neutral world中almost work的hedge在actual world中一定也almost surely work\n\n**Definition** 对于equivalent的两个概率测度以及它们之间的almost surely positive random variable, 这个随机变量$Z$称之为Radon-Nikodym derivative of$\\widetilde{\\mathbb{P}}$ with respect to $\\mathbb{P}$ and we write $Z=\\frac{d\\widetilde{\\mathbb{P}}}{d\\mathbb{P}}$, $Z$ 的存在性成为Radon-Nikodym Theorem\n\n# Information and Conditioning\n\n## Information and $\\sigma$-algebras\n\nThe hedge must specify what position we will take in the underlying security at each future time contingent on how the uncertainty between the present time and that future time is resolved.\n\n**resolve sets by information**\n\n$\\Omega$ is the set of 8 possible outcomes of 3 coin tosses,\n\n$A_H=\\{HHH,HHT,HTH,HTT\\},A_T=\\{THH,THT,TTH,TTT\\}$\n\nif we are told the first coin toss only. the four sets that are resolved by the first coin toss form the $\\sigma$-algebra\n\n$\\mathcal{F}_1=\\{\\phi,\\Omega,A_H,A_T\\}$\n\nthis $\\sigma$-algebra contains the information learned by observing the first coin toss.\n\n如果某几个集合是resolved,那么他们的并,以及各自的补也是resolved,符合$\\sigma$-algebra\n\n**Definition** let $\\Omega$ be a nonempty set. Let $T$ be a fixed positive number and assume that for each $t\\in [0,T]$ there is a $\\sigma-algebra$ $\\mathcal{F}(t)$. Assume further that if $s\\le t$, then every set in $\\mathcal{F}(s)$ is also in $\\mathcal{F}(t)$. Then we call the collection of $\\sigma-algebra$ $\\mathcal{F}(t)$ a filtration.\n\nAt time $t$ we can know whether the true $\\omega$ lies in a set in $\\mathcal{F}(t)$\n\nLet $\\Omega=C_0[0,T]$, and assign probability to the sets in $\\mathcal{F}=\\mathcal{F}(T)$, then the paths $\\omega\\in C_0[0,T]$ will be the paths of the **Brownian motion**.\n\n**Definition** Let $X$ be a random variable defined on a nonempty sample space $\\Omega$. The $\\sigma-algebra$ generated by $X$, denoted $\\sigma(X)$, is the collection of all subsets of $\\Omega$ of the form $\\{X\\in B\\}$, $B$\n **ranges over** the Borel subsets of $\\mathbb{R}$\n\n这里的区别和简并有点像,随机变量是本征值,Filtration是量子态\n\n**Definition** Let $X$ be a random variable defined on a nonempty sample space $\\Omega$. Let $\\mathcal{G}$ be a $\\sigma-algebra$ of subsets of $\\Omega$. If every set in $\\sigma(X)$ is also in $\\mathcal{G}$, we say that $X$ is $\\mathcal{G}-measurable$\n\n意味着$\\mathcal{G}$ 中的信息足够决定$X$ 的值。对于borel可测函数$f$,$f(X)$也是$\\mathcal{G}-measurable$的。对于多元函数同样成立\n\n**Definition** Let $\\Omega$ be a nonempty sample space equipped with a filtration $\\mathcal{F}(t)$. Let \n\n$X(t)$ be a collection of random variables indexed by $t\\in [0,T]$, We say this collection of random variables is an adapted stochastic process if, for each $t$, the random variable $X(t)$ is $\\mathcal{F}(t)-measurable$ \n\n## Independence\n\n对于一个随机变量和一个$\\sigma-algebra$ $\\mathcal{G}$, measurable 和 independent 是两种极端,但大部分情况下,$\\mathcal{G}$中但信息可以估计$X$, 但不足以确定$X$的值。\n\nIndependence会受到概率度量的影响,但measurability不会。\n\nprobability space $(\\Omega,\\mathcal{F},\\mathbb{P})$,$\\mathcal{G}\\in \\mathcal{F}, \\mathcal{H}\\in \\mathcal{F}$, $\\Omega$ 中的两个$\\sigma-algebra$$A$和$B$独立如果$\\mathbb{P}(A\\cap B)=\\mathbb{P}(A)\\cdot\\mathbb{P}(B)$, for all $A\\in \\mathcal{G},B\\in \\mathcal{H}$\n\n独立的定义可以拓展到随机变量($\\sigma-algebra$ they generate are independent)之间,随机变量与$\\sigma-algebra$之间。\n\n**Definition** $(\\Omega,\\mathcal{F},\\mathbb{P})$ is a probability space and let $\\mathcal{G}_1,\\mathcal{G}_2,\\mathcal{G}_3\\dots$ be a sequence of $sub-\\sigma-algebra$ of $\\mathcal{F}$. For a fixed positive integer n, we say that the n $\\sigma-algebra$s $\\mathcal{G}_1,\\mathcal{G}_2,\\mathcal{G}_3\\dots\\mathcal{G}_n$ are independent if$\\mathbb{P}(A_1\\cap A_2\\cap \\dots\\cap A_n)=\\mathbb{P}\n(A_1)\\mathbb{P}\n(A_2)\\dots \\mathbb{P}\n(A_n)$ for all $A_i\\in \\mathcal{G}_i$\n\n这个同样也可以拓展到随机变量之间以及随机变量与$\\sigma-algebra$之间。\n\n**Theorem** Let $X$ and $Y$ be independent random variables, and let $f$ and $g$ be Borel measurable functions on $\\mathbb{R}$. Then$f(X)$ and $g(Y)$ are independent random variables.\n\nPROOF\n\nLet $A$ be in the $\\sigma-algebra$ generated by $f(X)$. This $\\sigma-algebra$ is a $sub-\\sigma -algebra$ of $\\sigma(X)$. \n\n这很自然,every set in $A$ is of the form$\\{\\omega \\in \\Omega;f(X(\\omega))\\in C\\}\\text{,where }C\\text{ is a Borel subset of }\\mathbb{R}$. 只需要定义$D=\\{x\\in \\mathbb{R};f(x)\\in C\\}$. Then we know$A\\in \\sigma(X)$. Let $B$ be the $\\sigma-algebra$ gnenerated by $g(Y)$, then $B\\in \\sigma(Y)$. 由于$X,Y$独立,所以$A,B$独立。\n\n**Definition** Let$X$ and $Y$ be random variables. The pair of random variables$(X,Y)$ takes values in the plane$\\mathbb{R}^2$, and the joint distribution measure of $(X,Y)$ is given by$\\mu_{X,Y}(C)=\\mathbb{P}\\{(X,Y)\\in C\\}$ for all Borel sets $C\\in \\mathbb{R}^2$\n\n同样满足概率度量的两个条件:全空间测度为1,以及countable additivity preperty\n\n**Theorem** Let $X$ and $Y$ be random variables. The following conditions and equivalent.\n\n1. $X$ and $Y$ are independent\n2. the joint distribution measure factors:\n \n $\\mu_{X,Y}(A\\times B)=\\mu_X(A)\\mu_Y(B)$ for all Borel subsets$A\\in \\mathbb{R},B\\in\\mathbb{R}$\n \n3. the joint cumulative distribution function factors\n \n $F_{X,Y}(a,b)=F_X(a)F_Y(b)$ for all $a\\in \\mathbb{R},b\\in \\mathbb{R}$\n \n4. the joint moment-generating function factor:(矩母函数)\n \n $\\mathbb{E}e^{uX+vY}=\\mathbb{E}e^{uX}\\cdot\\mathbb{E}e^{vY}$\n \n5. the joint density factors(if there is one)\n \n $f_{X,Y}(x,y)=f_X(x)f_Y(y)$ for almost every$x\\in\\mathbb{R},y\\in\\mathbb{R}$\n \n\nconditions above imply but are not equivalent to:\n\n1. $\\mathbb{E}[XY]=\\mathbb{E}X\\cdot\\mathbb{E}Y$ provided $\\mathbb{E}|XY|<\\infty$\n\n**Definition** Let $X$ be a random variable whose expected value is defined. The variance of $X$, denoted $Var(X)$ is $Var(X)=\\mathbb{E}[(X-\\mathbb{E}X)^2]=\\mathbb{E}[X^2]-(\\mathbb{E}X)^2$\n\ncovariance of $X$ and $Y$ is $Cov(X,Y)=\\mathbb{E}[(X-\\mathbb{E}X)(Y-\\mathbb{E}Y)]=\\mathbb{E}[XY]-\\mathbb{E}X\\cdot\\mathbb{E}Y$\n\ncorrelation coefficient of $X$and $Y$ is $\\rho(X,Y)=\\frac{Cov(X,Y)}{\\sqrt{Var(X)Var(Y)}}$\n\nif $\\rho(X,Y)=0$, we say that $X$ and $Y$ are uncorrelated\n\n## General Conditional Expectations\n\n**Definition** Let$(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space, let $\\mathcal{G}$ be a sub-$\\sigma$-algebra of $\\mathcal{F}$, and let $X$ be a random variable that is either nonnegative or integrable. The conditional expectation of $X$ given $\\mathcal{G}$, denoted$\\mathbb{E}[X|\\mathcal{G}]$, is any random variable that satisfies\n\n1. **Measurability $\\mathbb{E}[X|\\mathcal{G}]$** is $\\mathcal{G}$ measurable\n2. **Partial averaging $\\int_A\\mathbb{E}[X|\\mathcal{G}(\\omega)]=\\int_AX(\\omega)d\\mathbb{P}(\\omega)$** for all $A\\in \\mathcal{G}$\n\nIf $\\mathcal{G}$ is generated by some other random variable $W$, then we can write$\\mathbb{E}[X|W]$\n\n(1) means although the estimate of $X$based on the information in $\\mathcal{G}$ is itself a random variable, the value of the estimate $\\mathbb{E}[X|\\mathcal{G}]$ can be determined from the information in $\\mathcal{G}$\n\n存在性可以由Radon-Nikodym Theorem证明\n\n唯一性的证明如下:If $Y$ and $Z$ both satisfy conditions, then their difference $Y-Z$ is as well, and thus the set $A=\\{Y-Z>0\\}$ is in $\\mathcal{G}$. 根据(2),$\\int_AY(\\omega)d\\mathbb{P}(\\omega)=\\int_AX(\\omega)d\\mathbb{P}(\\omega)=\\int_AZ(\\omega)d\\mathbb{P}(\\omega)$\n\nHence $Y=Z$ almost surely.\n\n**Theorem** Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space and let $\\mathcal{G}$ be a sub-$\\sigma$-algebra of $\\mathcal{F}$\n\n1. linearity of conditional expectations\n$\\mathbb{E}[c_1X+c_2Y|\\mathcal{G}]=c_1\\mathbb{E}[X|\\mathcal{G}]+c_2\\mathbb{E}[Y|\\mathcal{G}]$\n2. taking out what is known. \n \n If $X$ is $\\mathcal{G}$-measurable\n \n $\\mathbb{E}[XY|\\mathcal{G}]=X\\mathbb{E}[Y|\\mathcal{G}]$\n \n3. iterated conditioning.\n \n If $\\mathcal{H}$ is a sub-$\\sigma$-algebra of $\\mathcal{G}$ and $X$ is an integrable random variable, then\n \n $\\mathbb{E}[\\mathbb{E}[X|\\mathcal{G}]|\\mathcal{H}]=\\mathbb{E}[X|\\mathcal{H}]$\n \n4. independence\n \n If $X$ is independent of $\\mathcal{G}$, then $\\mathbb{E}[X|\\mathcal{G}]=\\mathbb{E}X$\n \n5. conditional Jensen’s inequality\n \n $\\mathbb{E}[\\phi(X)|\\mathcal{G}]\\ge\\phi(\\mathbb{E}[X|\\mathcal{G}])$\n \n\n**Lemma** Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space, and let $\\mathcal{G}$ be a sub-$\\sigma$-algebra of $\\mathcal{F}$. Suppose the random variables $X_1,\\dots,X_K$ are $\\mathcal{G}$-measurable and the random variables$Y_1,\\dots,Y_L$ are independent of $\\mathcal{G}$. Let $f(x_1,\\dots,x_K,y_1,\\dots,y_L)$ be a function of the dummy variables, and define: \n\n$g(x_1,\\dots,x_K)=\\mathbb{E}f(x1,\\dots,x_K,Y_1,\\dots,Y_L)$\n\nThis means holding $X_i$ constant and integrate out $Y_i$.\n\nThen,$\\mathbb{E}[f(X_1,\\dots,X_K,Y_1,\\dots,Y_L)|\\mathcal{G}]=g(X_1,\\dots,X_K)$\n\n**Definition** Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space, let $T$ be a fixed positive number, and let $\\mathcal{F}(t)$, $0\\le t\\le T$, be a filtration of $sub-\\sigma-algebra$ of $\\mathcal{F}$. Consider an adapted stochastic process $M(t)$:\n\n1. If $\\mathbb{E}[M(t)|\\mathcal{F}(s)]=M(s)$ for all $0\\le s\\le t \\le T$, this process is a ***martingale***. It has no tendency to rise or fall.\n2. If $\\mathbb{E}[M(t)|\\mathcal{F}(s)]\\le M(s)$ for all $0\\le s\\le t \\le T$, this process is a ***supermartingale***. It has no tendency to rise, it may have a tendency to fall.\n3. If $\\mathbb{E}[M(t)|\\mathcal{F}(s)]\\ge M(s)$ for all $0\\le s\\le t \\le T$, this process is a ***submartingale***. It has no tendency to fall, it may have a tendency to rise.\n\n**Definition** Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space, let $T$ be a fixed positive number, and let $\\mathcal{F}(t)$, $0\\le t\\le T$, be a filtration of $sub-\\sigma-algebra$ of $\\mathcal{F}$. Consider an adapted stochastic process $X(t)$. Assume that for all $0\\le s\\le t\\le T$ and for every nonnegative, Borel-measuable function $f$, there is another Borel-measuable function $g$ such that:\n\n$\\mathbb{E}[f(X(t))|\\mathcal{F}(s)]=g(X(s))$\n\nThen we say that the X is a Markov process\n\n# Brownian Motion\n\n## Scaled Random Walks\n\n### Symmetric Random Walk\n\nTo build a **symmetric random walk** we repeatedly toss a fair coin.\n\n$X_j=\\begin{cases}1 \\text{ if }\\omega_j=H\\\\\\\\-1\\text{ if }\\omega_j=T\\end{cases}$\n\n$M_0=0$, $M_k=\\sum_{j=1}^kX_j$\n\nthe process $M_k$ is a *symmetric random walk.*\n\n### Increments of the Symmetric Random Walk\n\nA random walk has independent increments(独立增量性)\n\nif we choose nonnegative integers$0=k_0<k_1<\\cdots<k_m$ , the random variables $M_{k_i}-M_{k_{i-1}}$ are independent.\n\nEach of these random variables $M_{k_i}-M_{k_{i-1}}=\\sum_{j=k_{i+1}}^{k_{i+1}}X_j$ is called an increment of the random walk. \n\nEach increment has expected value 0 and variance $k_{i+1}-k_i$ . The variance is obvious because $X_j$ are independent.\n\n### Martingale Property for the Symmetric Random Walk\n\nWe choose nonnegative integers $k<l$ and compute:\n\n$\\mathbb{E}[M_l|\\mathcal{F}_k]=\\mathbb{E}[(M_l-M_k)+M_k|\\mathcal{F}_k]=\\mathbb{E}[M_l-M_k|\\mathcal{F}_k]+\\mathbb{E}[M_k|\\mathcal{F}_k]=M_k$\n\n### Quadratic Variation of the Symmetric Random Walk\n\nthe quadratic variation up to time $k$ is defined to be $[M,M]_k=\\sum\\_{j=1}^k(M\\_j-M\\_{j-1})^2=k$\n\nThis is computed path-by-path. taking all the one step increments $M_j-M_{j-1}$ along that path, squaring these increments, and then summing them.\n\nNote that $[M,M]_k$ is the same as $Var(M_k)$, but the computations of these two quantities are quite different. $Var$ is computed by taking an average over all paths, taking their probability into account. If the random walk is not symmetric, the probability distribution would affect $Var$. On the contrary, the probability up and down do not affect the quadratic variation computation.\n\n### Scaled Symmetric Random Walk\n\nWe fix a positive integer $n$ and define the **scaled symmetric random walk** $W^{(n)}(t)=\\frac{1}{\\sqrt{n}}M_{nt}$. If $nt$ is not an integer, we define $W^{(n)}(t)$ by linear interpolation between its values at the nearest points $s$ and $u$ to the left and right of $t$ for which $ns$ and $nu$ are integers. \n\nA Brownian motion is a scaled symmetric random walk with $n\\to \\infty$\n\n$\\mathbb{E}(W^{(n)}(t)-W^{(n)}(s))=0,Var(W^{(n)}(t)-W^{(n)}(s))=t-s$\n\nLet $0\\le s\\le t$ be given, and decompose $W^{(n)}(t)$ as: $W^{(n)}(t)=(W^{(n)}(t)-W^{(n)}(s))+W^{(n)}(s)$ \n\n$(W^{(n)}(t)-W^{(n)}(s))$ is independent of $\\mathcal{F}(s)$, the $\\sigma-algebra$ of information available at time s, and $W^{(n)}(s)$ is $\\mathcal{F}(s)$ measurable. So $\\mathbb{E}[W^{(n)}(t)|\\mathcal{F}(s)]=W^{(n)}(s)$\n\nThe **quadratic variation** of the scaled random walk: \n\n$\\[W^{(n)},W^{(n)}\\]\\(t\\)=\\sum\\_{j=1}^{nt}[W^{(n)}(\\frac{j}{n})-W^{(n)}(\\frac{j-1}{n})]^2=\\sum\\_{j=1}^{nt}[W^{(n)}[\\frac{1}{\\sqrt{n}}X_j]^2=\\sum\\_{j=1}^{nt}\\frac{1}{n}=t$\n\n### Limiting Distribution of the Scaled Random Walk\n\n**Theorem: Central limit** Fix $t\\ge 0$. As $n\\to \\infty$, the distribution of the scaled random walk $W^{(n)}(t)$ evaluated at time $t$ converges to the normal distribution with mean zero and variance $t$.\n\nPROOF\n\nFor the normal density $f(s)=\\frac{1}{\\sqrt{2\\pi t}}e^{-\\frac{x^2}{2t}}$, the moment-generating function is \n\n$\\phi(u)=\\frac{1}{\\sqrt{2\\pi t}}\\int_{-\\infty}^\\infty \\exp\\{ux-\\frac{x^2}{2t}\\}dx=e^{\\frac{1}{2}u^2t}$\n\nIf $t$ is such that $nt$ is an integer, then the moment-generating function for $W^{(n)}(t)$ is:\n\n$\\phi_n(u)=\\mathbb{E}e^{uW^{(n)}(t)}=\\mathbb{E}\\exp\\{\\frac{u}{\\sqrt{n}}M_{nt}\\}=\\mathbb{E}\\exp\\{\\frac{u}{\\sqrt{n}}\\sum_{j=1}^{nt}X_j\\}=\\mathbb{E}\\prod_{j=1}^{nt}\\exp\\{\\frac{u}{\\sqrt{n}}X_j\\}\\\\\\\\=\\prod_{j=1}^{nt}\\mathbb{E}\\exp\\{\\frac{u}{\\sqrt{n}}X_j\\}=\\prod_{j=1}^{nt}(\\frac{e^{\\frac{u}{\\sqrt{n}}}+e^{\\frac{-u}{\\sqrt{n}}}}{2})=(\\frac{e^{\\frac{u}{\\sqrt{n}}}+e^{\\frac{-u}{\\sqrt{n}}}}{2})^{nt}$\n\nwhen $n\\to \\infty$ , $\\phi(u)=e^{\\frac{1}{2}u^2t}$\n\n### Log-Normal Distribution as the Limit of the Binomial Model\n\nWe build a model for a stock price on the time interval from $0$ to $t$ by choosing an integer $n$ and constructing a binomial model for the stock price that takes $n$ steps per unit time. Up factor $u_n=1+\\frac{\\sigma}{\\sqrt{n}}$, down factor $u_d=1-\\frac{\\sigma}{\\sqrt{n}}$. $r=0.$\n\nThe risk-neutral probabilities are then:\n\n$\\tilde{p}=\\frac{1+r-d_n}{u_n-d_n}=\\frac{1}{2}$, $\\tilde{q}=\\frac{u_n-1-r}{u_n-d_n}=\\frac{\\sigma/\\sqrt{n}}{2\\sigma/\\sqrt{n}}=\\frac{1}{2}$\n\nRandom walk $M_{nt}=H_{nt}-T_{nt}$, while $nt=H_{nt}+T_{nt}$\n\nthe stock price at time $t$ is $S_n(t)=S(0)u_n^{H_{nt}}d_n^{T_{nt}}=S(0)(1+\\frac{\\sigma}{\\sqrt{n}})^{\\frac{1}{2}(nt+M_{nt})}(1+\\frac{\\sigma}{\\sqrt{n}})^{\\frac{1}{2}(nt+M_{nt})}(1-\\frac{\\sigma}{\\sqrt{n}})^{\\frac{1}{2}(nt-M_{nt})}$\n\nwe need to identify the distribution of this random variable as $n\\to \\infty$\n\n**Theorem** As $n\\to \\infty$ , the distribution of $S_n(t)$ converges to the distribution of\n\n$S(t)=S(0)\\exp\\{\\sigma W(t)-\\frac{1}{2}\\sigma^2t\\}$ \n\n$W(t)$ is a normal random variable with mean zero and variance $t$\n\nPROOF:\n\n$\\log S_n(t)\\\\\\\\=\\log S(0)+\\frac{1}{2}(nt+M_{nt})\\log (1+\\frac{\\sigma}{\\sqrt{n}})+\\frac{1}{2}(nt-M_{nt})\\log (1-\\frac{\\sigma}{\\sqrt{n}})\\\\\\\\=\\log S(0)+\\frac{1}{2}(nt+M_{nt})(\\frac{\\sigma}{\\sqrt{n}}-\\frac{\\sigma^2}{2n}+O(n^{-3/2}))+\\frac{1}{2}(nt-M_{nt})(\\frac{\\sigma}{-\\sqrt{n}}-\\frac{\\sigma^2}{2n}+O(n^{-3/2}))\\\\\\\\=\\log S(0)+nt(-\\frac{\\sigma^2}{2n}+O(n^{-3/2}))+M_{nt}(\\frac{\\sigma}{\\sqrt{n}}+O(n^{-3/2}))=\\log S(0)-\\frac{1}{2}\\sigma^2t+\\sigma W^{(n)}(t)$\n\nBy the **Central Limit Theorem,** we know that $\\frac{1}{\\sqrt{n}}M_{nt}=W^{(n)}(t)\\to W(t), \\text{when }n\\to \\infty$\n\n## Brownian Motion\n\n### Definition of Brownian Motion\n\n**Definition** Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space. For each $\\omega\\in\\Omega$, suppose there is a continuous function $W(t)$ of $t\\ge 0$ that satisfies $W(0)=0$ that depends on $\\omega$. Then $W(t),t\\ge 0$ is a Brownian motion if for all $t_i$ the increments $W(t_i)-W(t_{i-1})$ are independent and each of these increments is normally distributed with $\\mathbb{E}[W(t_{i+1})-W(t_i)]=0,Var[W(t_{i+1})-W(t_i)]=t_{i+1}-t_i$\n\nDifference between BM and a scaled random walk: the scaled random walk has a natural time step and is linear between these time steps, whereas the BM has no linear pieces.\n\n### Distribution of Brownian Motion\n\nFor any two times, the covariance of $W(s)$ and $W(t)$ for $s\\le t$ is\n\n$\\mathbb{E}[W(s)W(t)]=\\mathbb{E}[W(s)(W(t)-W(s))+W^2(s)]=\\mathbb{E}[W(s)]\\mathbb{E}[(W(t)-W(s))]+\\mathbb{E}[W^2(s)]=s$\n\nWe compute the moment-generating function of the random vector$(W(t_1),W(t_2),\\dots,W(t_m))$\n\n$\\phi=\\mathbb{E}\\exp\\{u_mW(t_m)+\\dots+u_1W(t_1)\\}=\\mathbb{E}\\exp\\{u_m(W(t_m)-W(t_{m-1}))+\\dots+(u_1+u_2+\\dots+u_m)W(t_1)\\}=\\mathbb{E}\\exp\\{u_m(W(t_m)-W(t_{m-1}))\\}\\cdots \\mathbb{E}\\exp\\{(u_1+u_2+\\cdots+u_m)W(t_1)\\}=\\exp\\{\\frac{1}{2}u_m^2(t_m-t_{m-1})\\}\\cdots\\exp\\{(u_1+u_2+\\cdots+u_m)^2t_1\\}$\n\nThe distribution of the Brownian increments can be specified by specifying the joint density or the joint moment-generating function of the random variables\n\n**Theorem** Let$(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space. For each $\\omega\\in\\Omega$, suppose there is a continuous function $W(t)$ of $t\\ge 0$ that satisfies $W(0)=0$ and that depends on $\\omega$. \n\n1. For all $0< t_0< t_1\\cdots <t_m$, the increments are independent and each of these increments is normally distributed with mean and variance given by$\\mathbb{E}[W(t_{i+1})-W(t_i)]=0,Var[W(t_{i+1})-W(t_i)]=t_{i+1}-t_i$\n2. For all $0< t_0< t_1\\cdots <t_m$, the random variables $W(t_i)$ are jointly normally distributed with means equal to zero and covariance matrix\n \n $\\begin{pmatrix} t_{1} &t_1 \\cdots & t_{1} \\\\\\\\ t_1&t_2\\cdots &t_2\\\\\\\\ \\vdots & \\ddots & \\vdots \\\\\\\\ t_{1} &t_2 \\cdots & t_{m} \\end{pmatrix}$ \n \n3. the random variables have the joint moment-generating function mentioned before\n\n### Filtration for Brownian Motion\n\n**Definition** Let$(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space on which is defined a Brownian motion $W(t),t\\ge 0$. A filtration for the Brownian motion is a collection of $\\sigma$-algebra $\\mathcal{F}(t),t\\ge 0$, satisfying:\n\n1. **Information accumulates**\n2. **Adaptivity: $W(t)$** is **$\\mathcal{F}(t)$**-measurable\n3. **Independence of future increments**\n\n$\\Delta(t),t\\ge0$, be a stochastic process. $\\Delta(t)$ is adapted to the filtration $\\mathcal{F}(t)$ if for each $t\\ge 0$ the random variable $\\Delta(t)$ if $\\mathcal{F}(t)$-measurable.\n\nThere are two possibilities for the filtration $\\mathcal{F}(t)$ for a Brownian motion. \n\n1. to let $\\mathcal{F}(t)$ contain only the info obtained by observing the BM itself up to time $t$. \n2. to include in $\\mathcal{F}(t)$ info obtained by observing the BM and one or more other processes. But if the info in $\\mathcal{F}(t)$ includes observations of processes other than the BM $W$, this additional info is not allowed to give clues about the future increments because of property iii\n\n### Martingale Property for Brownian Motion\n\n**Theorem** Brownian motion is a martingale\n\n## Quadratic Variation\n\nFor BM, there is no natural step size. If we are given $T>0$, we could simply choose a step size, say $\\frac{T}{n}$ for some large $n$, and compute the quadratic variation up to time $T$ with this step size:\n\n$\\sum_{j=0}^{n-1}[W(\\frac{(j+1)T}{n})-W(\\frac{jT}{n})]^2$\n\nThe variation of paths of BM is not zero, which makes stochastic calculus different from ordinary calculus\n\n### First-Order Variation\n\n$FV_T(f)=|f(t_1)-f(0)|+|f(t_2)-f(t_1)|+\\dots+|f(T)-f(t_2)|=\\int_0^{t_1}f'(t)dt+\\dots+\\int_{t_2}^Tf'(t)dt=\\int_0^T|f'(t)|dt$\n\nWe first choose a partition $\\Pi=\\{t_0,t_1,\\dots,t_n\\}$ of $[0,T]$, which is a set of times. These will serve to determine the step size. The maximum step size of the partition will be denoted $\\Vert\\Pi\\Vert=\\max_{j=0,\\dots,n-1}(t_{j+1}-t_j)$. We then define:\n\n$FV_T(f)=\\lim_{\\Vert\\Pi\\Vert\\to0}\\sum_{j=0}^{n-1}\\vert f(t_{j+1})-f(t_j)\\vert$\n\n用中值定理可以证明与积分相等\n\n### Quadratic Variation\n\n**Definition** Let $f(t)$ be a function defined for $0\\le t\\le T$. The quadratic variation to $f$ up to time $T$ is \n\n$[f,f]\\(T\\)=\\lim\\_{\\Vert\\Pi\\Vert\\to0}\\sum\\_{j=0}^{n-1}\\vert f(t\\_{j+1})-f(t\\_j)\\vert$\n\nif $f$ is derivative, then $[f,f](T)=0$\n\nif $\\int_0^T\\vert f'(t^*_j)\\vert ^2dt$ is infinite, then $[f,f]\\(T\\)$ lead to a $0\\cdot\\infty$ situation, which can be anything between $0$ and $\\infty$\n\n**Theorem** Let $W$ be a Brownian motion. Then $[W,W]\\(T\\)=T$ for all $T\\ge 0$ almost surely.\n\nPROOF\n\nDefine the *sample quadratic variation* corresponding to the partition of $[0,T]$, $\\Pi =\\{t_0,t_1,\\dots,t_n\\}$ to be\n\n $Q_\\Pi=\\sum_{j=0}^{n-1}(W(t_{j+1})-W(t_j))^2$\n\nWe can show that $Q_\\Pi$ converges to $T$ as $\\Vert\\Pi\\Vert\\to0$\n\n$\\mathbb{E}[(W(t_{j+1})-W(t_j))^2]=Var[W(t_{j+1})-W(t_j)]=t_{j+1}-t_j$ implies:\n\n$\\mathbb{E}Q_\\Pi=\\sum\\mathbb{E}[(W(t_{j+1})-W(t_j))^2]=\\sum(t_{j+1}-t_j)=T$\n\n$Var[(W(t_{j+1})-W(t_j))^2]=\\mathbb{E}[(W(t_{j+1})-W(t_j))^4]-2(t_{j+1}-t_j)\\mathbb{E}[(W(t_{j+1})-W(t_j))^2]+(t_{j+1}-t_j)^2$\n\n$\\mathbb{E}[(W(t_{j+1})-W(t_j))^4]=3(t_{j+1}-t_j)^2$,$\\mathbb{E}[(W(t_{j+1})-W(t_j))^2]=t_{j+1}-t_j$\n\nPROOF\n\nBy Ito’s formula, we have\n\n$𝑊^4(t)=4\\int^𝑡_0𝑊^3_s𝑑𝑊_s+6\\int^𝑡_0𝑊^2_sds$\n\n$M(t):=\\int_0^tW_s^3dW_s=0$ is a martingale and $\\mathbb{E}M(t)=\\mathbb{E}M(0)=0$\n\n$\\mathbb{E}W^4(t)=6\\int_0^t\\mathbb{E}[W_s^2]ds=6\\int_0^tsds=3t^2$\n\nso $Var[(W(t_{j+1}-W(t_j))^4]=2(t_{j+1}-t_j)^2$\n\nand $Var(Q_\\Pi)=\\sum 2(t_{j+1}-t_j)^2\\le2\\Vert\\Pi\\Vert T$\n\nIn particular, $\\lim_{\\Vert\\Pi\\Vert\\to 0}Var(Q_\\Pi)=0,lim_{\\Vert\\Pi\\Vert\\to0}Q_\\Pi=\\mathbb{E}Q_\\Pi=T$\n\n$(W(t_{j+1})-W(t_j))^2\\approx t_{j+1}-t_j$$(W(t_{j+1})-W(t_j))^2=t_{j+1}-t_j$ when $t_{j+1}-t_j$ is very small\n\n$dW(t)dW(t)=dt$ is the informal write\n\n$dWdt=0,dtdt=0$\n\n### Volatility of Geometric Brownian Motion\n\ngeometric Brownian motion: $S(t)=S(0)\\exp\\{\\sigma W(t)+(\\alpha-\\frac{1}{2}\\sigma^2)t\\}$\n\nrealized volatility: the sum of the squares of the log returns\n\nfor $T_1=t_0<t_1<\\cdots<tm=T_2$,\n\n$\\sum (\\log\\frac{S(t_{j+1})}{S(t_j)})^2=\\sigma^2\\sum(W(t_{j+1})-W(t_j))^2+(\\alpha-\\frac{1}{2}\\sigma^2)^2\\sum(t_{j+1}-t_j)^2+2\\sigma (\\alpha-\\frac{1}{2}\\sigma^2)\\sum(W(t_{j+1})-W(t_j))(t_{j+1}-t_j)$\n\nWhen the maximum step size $\\Vert\\Pi\\Vert=\\max_{j=0,1,\\dots,m-1}(t_{j+1}-t_j)$ is small, then the first term is approximately equal to its limit $\\sigma^2(T_2-T_1)$,hence, we have:\n\n$\\frac{1}{T_2-T_1}\\sum(\\log\\frac{S(t_{j+1})}{S(t_j)})^2\\approx\\sigma^2$\n\n## Markov Property\n\n**Theorem** Let$W(t),t\\ge0$, be a Brownian motion and let $\\mathcal{F}(t),t\\ge0$ Be a filtration for this Brownian motion. Then $W(t)$ is a Markov process\n\nPROOF\n\nWe need to show: $\\mathbb{E}[f(W(t))\\vert \\mathcal{F}(s)]=g(W(s))$ $g$ Exists whenever given $0\\le s\\le t,f$\n\n$\\mathbb{E}[f(W(t))\\vert\\mathcal{F}(s)]=\\mathbb{E}[f((W(t)-W(s))+W(s))\\vert\\mathcal{F}(s)]$\n\n$W(t)-W(s)$ is normally distributed with mean zero and variance $t-s$\n\nReplace $W(s)$ with a dummy variable $x$\n, define $g(x)=\\mathbb{E}f(W(t)-W(s)+x)$, then \n\n$g(x)=\\frac{1}{\\sqrt{2\\pi(t-s)}}\\int f(w+x)\\exp\\{-\\frac{w^2}{2(t-s)}\\}dw=\\frac{1}{\\sqrt{2\\pi\\tau}}\\int f(y)\\exp\\{-\\frac{(y-x)^2}{2\\tau}\\}dy$\n\nDefine the *transition density $p(\\tau,x,y):=\\frac{1}{\\sqrt{2\\pi\\tau}}e^{-\\frac{(y-x)^2}{2\\tau}},\\tau=t-s$*\n\n$g(x)=\\int f(y)p(\\tau,x,y)dy$ \n\nAnd $\\mathbb{E}[f(W(t))\\vert\\mathcal{F}(s)]=\\int f(y)p(\\tau,W(s),y)dy$\n\nConditioned on the information in $\\mathcal{F}(s)$, the conditional density of $W(t)$ is $p(\\tau,W(s),y)$. This is a density in the variable $y$, normal with mean $W(s)$ and variance $\\tau$. The only information from $\\mathcal{F}(s)$ that is relevant is the value of $W(s)$\n\n## First Passage Time Distribution\n\nexponential martingale corresponding to $\\sigma$: $Z(t)=\\exp\\{\\sigma W(t)-\\frac{1}{2}\\sigma^2t\\}$\n\n**Theorem** Exponential martingale Let $W(t),t\\ge 0$, be a Brownian motion with a filtration $\\mathcal{F}(t),t\\ge 0$, and let $\\sigma$ be a constant, thew process $Z(t)$ is a martingale\n\nPROOF\n\n$\\mathbb{E}[Z(t)\\vert\\mathcal{F}(s)]=\\mathbb{E}[\\exp\\{\\sigma W(t)-\\frac{1}{2}\\sigma^2t\\}\\vert \\mathcal{F}(s)]=\\mathbb{E}[\\exp\\{\\sigma (W(t)-W(s))\\}\\cdot\\exp\\{\\sigma W(s)-\\frac{1}{2}\\sigma^2t\\}\\vert \\mathcal{F}(s)]=\\exp\\{\\sigma W(s)-\\frac{1}{2}\\sigma^2t\\}\\cdot\\mathbb{E}[\\exp\\{\\sigma (W(t)-W(s))\\}]$\n\n$W(t)-W(s)$ is a normal distribution with mean zero and variance $\\sigma$ so $\\mathbb{E}[\\exp\\{\\sigma (W(t)-W(s))\\}]=\\frac{1}{2}\\sigma^2(t-s)$\n\n$\\mathbb{E}[Z(t)\\vert\\mathcal{F}(s)]=Z(s)$\n\nLet $m$ be a real number, and define the first passage time to level $m$: $\\tau_m=\\min\\{t\\ge 0;W(t)=m\\}$ if the BM never reaches the level $m$, we set $\\tau_m=\\infty$. A martingale that is stopped at a stopping time is still martingale and thus must have constant expectation. So:\n\n$1=Z(0)=\\mathbb{E}Z(t\\land\\tau_m)=\\mathbb{E}[\\exp\\{\\sigma W(t\\land\\tau_m)-\\frac{1}{2}\\sigma^2(t\\land\\tau_m)\\}]$ $t\\land\\tau_m$ means the minimum of $t$ and $\\tau_m$\n\nIf $\\tau_m<\\infty$, the term $\\exp\\{-\\frac{1}{2}\\sigma^2(t\\land\\tau_m)\\}$ is equal to $\\exp\\{-\\frac{1}{2}\\sigma^2\\tau_m\\}$ for large enough $t$. $\\tau_m=\\infty$, the result converges to zero. So: \n\n$\\lim\\_{t\\to\\infty\\}\\exp\\{\\sigma W\\(t\\land\\tau_m\\)-\\frac{1}{2}\\sigma^2(t\\land\\tau_m)\\}=\\mathbb{I}_\\{\\{\\tau_m<\\infty\\}}\\exp\\{\\sigma m-\\frac{1}{2}\\sigma^2\\tau_m\\\\}$\n\nnow we can obtain:\n\n$1=\\mathbb{E}[\\mathbb{I}_{\\{\\tau_m<\\infty\\}}\\exp\\{\\sigma m-\\frac{1}{2}\\sigma^2\\tau_m\\}]$\n\n$\\mathbb{E}[\\mathbb{I}_{\\{\\tau_m<\\infty\\}}\\exp\\{-\\frac{1}{2}\\sigma^2\\tau_m\\}]=e^{-\\sigma m}$\n\nwhen $\\sigma\\to0$, we get $\\mathbb{P}\\{\\tau_m<\\infty\\}=1$\n\n$\\tau_m$ is finite almost surely, so we may drop the indicator to obtain:\n\n$\\mathbb{E}[\\exp\\{-\\frac{1}{2}\\sigma^2\\tau_m\\}]=e^{-\\sigma m}$\n\n**Theorem** For $m\\in \\mathbb{R}$, the first passage time of Brownian motion to level $m$ is finite almost surely, and the Laplace transform of its distribution is given by \n\n$\\mathbb{E}e^{-\\alpha \\tau_m}=e^{-\\vert m \\vert\\sqrt{2\\alpha}}$ for all $\\alpha>0$\n\ndifferentiation: $\\mathbb{E}[\\tau_me^{-\\alpha\\tau_m}]=\\frac{\\vert m\\vert}{\\sqrt{2\\alpha}}e^{-\\vert m\\vert\\sqrt{2\\alpha}}$ for all $\\alpha>0$\n\nlet $\\alpha\\to 0$ get obtain $\\mathbb{E}\\tau_m=\\infty$ so long as $m\\neq0$\n\n## Reflection Principle\n\n### Reflection Equality\n\nfor each Brownian motion path that reaches level m prior to time t but is at a level w below m at time t, there is a \"reflected path\" that is at level $2m-w$ at time $t$. This reflected path is constructed by switching the up and down moves of the Brownian motion from time $\\tau_m$onward.\n\n**Reflection equality**\n\n$\\mathbb{P}\\{\\tau_m\\le t,W(t)\\le w\\}=\\mathbb{P}\\{W(t)\\ge 2m-w\\},w\\le m,m>0$\n\n### First Passage Time Distribution\n\n**Theorem** For all $m\\neq0$, the random variable $\\tau_m$ has cumulative distribution function:\n\n$\\mathbb{P}\\{\\tau_m\\le t\\}=\\frac{2}{\\sqrt{2\\pi}}\\int_{\\frac{\\vert m\\vert}{\\sqrt{t}}}^\\infty e^{-\\frac{y^2}{2}}dy$\n\n$f_{\\tau_m}(t)=\\frac{d}{dt}\\mathbb{P}=\\frac{\\vert m\\vert}{t\\sqrt{2\\pi t}}e^{-\\frac{m^2}{2t}}$\n\nPROOF\n\nUse the reflection equality, we obtain\n\n$\\mathbb{P}\\{\\tau_m\\le t,W(t)\\le m\\}=\\mathbb{P}\\{W(t)\\ge m\\}$\n\nif $W(t)\\ge m$, then we are guaranteed that $\\tau_m\\le t$. \n\n$\\mathbb{P}\\{\\tau_m\\le t,W(t)\\ge m\\}=\\mathbb{P}\\{W(t)\\ge m\\}$\n\nso,$\\mathbb{P}\\{\\tau_m\\le t\\}=2\\mathbb{P}\\{W(t)\\ge m\\}=\\frac{2}{\\sqrt{2\\pi t}}\\int_{m}^\\infty e^{-\\frac{x^2}{2t}}dx=\\frac{2}{\\sqrt{2\\pi}}\\int_{\\frac{\\vert m\\vert}{\\sqrt{t}}}^\\infty e^{-\\frac{y^2}{2}}dy$\n\n### Distribution of Brownian Motion and Its Maximum\n\ndefine the **maximum to date** for Brownian motion\n\n$M(t)=\\max_{0\\le s\\le t}W(s)$\n\nUse the reflection equality, we can obtain the joint distribution of $W(t)$\n and $M(t)$\n\n**Theorem** For $t>0$, the joint density of $(M(t),W(t))$ is\n\n$f_{M(t),W(t)}(m,w)=\\frac{2(2m-w)}{t\\sqrt{2\\pi t}}e^{-\\frac{(2m-w)^2}{2t}}$\n\nPROOF\n\n$\\mathbb{P}\\{M(t)\\ge m,W(t)\\le w\\}=\\int_m^\\infty\\int_{-\\infty}^wf_{M(t),W(t)}(x,y)dydx$\n\n$\\mathbb{P}\\{W(t)\\ge 2m-w\\}=\\frac{1}{\\sqrt{2\\pi t}}\\int_{2m-w}^\\infty e^{-\\frac{z^2}{2t}}dz$\n\nFrom the reflection equality, \n\n$\\frac{1}{\\sqrt{2\\pi t}}\\int_{2m-w}^\\infty e^{-\\frac{z^2}{2t}}dz= \\int_m^\\infty\\int_{-\\infty}^wf_{M(t),W(t)}(x,y)dydx$\n\nDifferentiate with respect to $m$\n\n$-\\int_{-\\infty}^wf_{M(t),W(t)}(m,y)dy=-\\frac{2}{\\sqrt{2\\pi t}}e^{-\\frac{(2m-w)^2}{2t}}$\n\nWith respect to $w$, then we obtain the distribution\n\n**Corollary** \n\nThe conditional distribution of $M(t)$ given $W(t)=w$ is $f_{M(t)\\vert W(t)}(m\\vert w)=\\frac{2(2m-w)}{t}e^{-\\frac{2m(m-w)}{t}}$","source":"_posts/Stochastic Calculus.md","raw":"---\nlayout: posts\ntitle: Stochastic Calculus for Finance\ndate: 2022-01-25\ncategories: 学习笔记\ntags: [金融,数学]\n\n---\n\n<head>\n <script src=\"https://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML\" type=\"text/javascript\"></script>\n <script type=\"text/x-mathjax-config\">\n MathJax.Hub.Config({\n tex2jax: {\n skipTags: ['script', 'noscript', 'style', 'textarea', 'pre'],\n inlineMath: [['$','$']]\n }\n });\n </script>\n</head>\n\n\n# General Probability Theory\n\n## infinite probability spaces\n\n### $\\sigma$-代数\n\n$\\sigma-algebra$, F is a collection of subsets of $\\Omega$\n\n1. empty set belongs to it\n2. whenever a set belongs to it, its complement also belong to F\n3. the union of a sequence of sets in F belongs to F\n\n可以有推论:\n\n1. $\\Omega$ 一定在F中\n2. 集合序列的交集也一定在F中\n\n### 概率测量的定义 probability measure\n\n一个函数,定义域是F中的任意集合,值域是[0,1],满足:\n\n1. $P(\\Omega)=1$\n2. $P(\\cup^\\infty_{n=1} A_n)=\\sum^\\infty_{n=1} P(A_n)$\n \n $triple(\\Omega,F,P)$称为概率空间\n \n\nuniform(Lebesgue)measure on [0,1]:在0,1之间选取一个数,定义:\n\n$P(a,b)=P[a,b]=b-a,0\\le a \\le b\\le 1$\n\n可以用上述方式表述概率的集合的集合构成了sigma代数,从包含的所有闭区间出发,称为Borel sigma代数\n\n$(a,b)=\\cup_{n=1}^\\infty[a+\\frac{1}{n},b-\\frac{1}{n}]$ ,所以sigma代数中包含了所有开区间,分别取补集可以导出包含开区间与闭区间的并,从而导出所有集合 \n\n通过从闭区间出发,添加所有必要元素构成的sigma代数称之为$Borel \\quad\\sigma-algebra$ of subsets of [0,1] and is denoted B[0,1]\n\nevent A occurs almost surely if P(A)=1\n\n## Random variables and distributions\n\ndefinition: a random variable is a real-valued function X defined on $\\Omega$ with the property that for every Borel subset B of **R,** the subset of $\\Omega$ given by:\n\n$$\n\\begin{equation*}\\{x\\in B\\}=\\{\\omega \\in \\Omega ; X(\\omega )\\in B\\}\\end{equation*}\n$$\n\nis in the $\\sigma$-algebra F\n\n本质是把事件映射为实数,同时为了保证可以拟映射,要求函数可测。\n\n构造R的Borel子集?从所有的闭区间出发,闭区间的交——特别地,开区间也包含进来,从而开集包含进来 ,因为每个开集可以写成开区间序列的并。闭集也是Borel集合,因为是开集的补集。\n\n关注X取值包含于某集合而不是具体的值\n\nDefinition: let X be a random variable on a probability space, the distribution measure of X is the probability measure $\\mu _X$that assigns to each Borel subset B of R the mass $\\mu _X(B)=P\\{X\\in B\\}$ \n\nRandom variable 有distribution 但两者不等同,两个不同的Random variable 可以有相同的distribution,一个单独的random variable 可以有两个不同的distribution\n\ncdf:$F(x)=P\\{X\\le x\\}$\n\n$\\mu_X(x,y]=F(y)-F(x)$\n\n## Expectations\n\n$E(X)=\\sum X(\\omega )P(\\omega )$\n\n$\\{\\Omega , F, P\\}$ random variable $X(\\omega )$ P是概率空间中的测度\n\n$A_k=\\{\\omega \\in \\Omega ; y_k\\le X(\\omega ) < y_{k+1}\\}$\n\nlower Lebesgue sum $LS^-_{\\Pi}=\\sum y_k P(A_k)$\n\nthe maximal distance between the $y_k$ partition points approaches zero, we get Lebesgue integral$\\int_{\\Omega}X(\\omega )dP(\\omega)$\n\nLebesgue integral相当于把积分概念拓展到可测空间,而不是单纯的更换了求和方式。横坐标实际上是$\\Omega$的测度。\n\nif the random variables X can take both positive and negative values, we can define the positive and negative parts of X:\n\n$X^+=max\\{X,0\\}$, $X^-=min\\{-X,0\\}$\n\n$\\int XdP=\\int X^+dP-\\int X^- dP$\n\n**Comparison**\n\nIf $X\\le Y$ almost surely, and if the Lebesgue integral are defined, then\n\n$\\int _{\\Omega}X(\\omega)dP(\\omega)\\le \\int _{\\Omega}Y(\\omega)dP(\\omega)$\n\nIf $X=Y$ almost surely, and if the Lebesgue integral are defined, then\n\n$\\int _{\\Omega}X(\\omega)dP(\\omega)=\\int _{\\Omega}Y(\\omega)dP(\\omega)$\n\n**Integrability, Linearity ...**\n\n**Jensen’s inequality**\n\nif $\\phi$ is a convex, real-valued function defined on R and if $E|X|<\\infty$ ,then\n\n$\\phi(EX)\\le E\\phi(X)$\n\n$\\mathcal{B} (\\mathbb{R})$ be the sigma-algebra of Borel subsets of $\\mathbb{R}$, the Lebesgue measure $\\mathcal{L}$ on R assigns to each set $B\\in \\mathcal{B}(\\mathbb{R})$ a number in $[0,\\infty)$ or the value $\\infty$ so that:\n\n1. $\\mathcal{L}[a,b] =b-a$ \n2. if $B_1,B_2,B_3 \\dots$ is a sequence of disjoint sets in $\\mathcal{B}$ ,then we have the countable additivity property: $\\mathcal{L} (\\cup_{n=1}^\\infty B_n)=\\sum_{n=1}^\\infty \\mathcal{L} (B_n)$\n\n黎曼积分有且只有在区间中非连续点的集合的Lebesgue测度为零时有定义,即f在区间上几乎处处连续\n\n若f的Riemann积分在区间上存在,则f是Borel可测的,而且Riemann积分和Lebesgue积分一致。\n\n### convergence of integrals\n\n**definition**\n\n$X_1,X_2,X_3\\dots$ be a sequence of random variables on the same probability space$(\\Omega, \\mathcal{F},\\mathbb{P})$, $X$ be another random variable. $X_1,X_2,X_3\\dots$ converges to $X$ almost surely $lim_{n\\to \\infty}X_n=X$ almost surely. if the set of $\\omega \\in \\Omega$ for the sequence has limit $X(\\omega)$ is a set with probability one. \n\nStrong law of Large Numbers: \n\n实的Borel可测的函数列$f_1,f_2,f_3\\dots$ defined on$\\mathbb{R}$, $f$ 也是实的Borel可测函数,the sequence converges to f almost every-where if 序列极限不为f的点的集合的 Lebesgue measure为零\n\n$lim_{n\\to \\infty}f_n=f \\textit{ almost everywhere}$\n\n当随机变量几乎趋于一致,他们的期望值趋于极限的期望。类似地,当函数几乎处处converge,通常情况下,他们的lebesgue积分收敛到极限的积分。特殊的情况,就是\n\n$lim_{n\\to \\infty}\\int f_n(x)dx\\ne \\int lim_{n\\to \\infty} f_n(x)dx$\n\n例如f是正态分布,左边为1,右边lebesgue积分为0\n\n**theorem** *Monotone convergence* $X_1,X_2,X_3\\dots$ be a sequence of random variables converging almost surely to another random variable $X$ if 序列几乎单调不减,期望的极限是EX\n\n$lim_{n \\to \\infty}\\mathbb{E}X_n=\\mathbb{E} X$\n\n把这里的随机变量换成Borel可测实值函数,也是成立的\n\n$lim_{n\\to \\infty}\\int_{-\\infty}^{\\infty}f_n(x)dx=\\int_{-\\infty}^{\\infty}f(x)dx$\n\n即使随机变量几乎不发散,但期望可能发散\n\n**theorem Dominated convergence** 如果随机变量序列几乎趋于一致于$X$,且满足 $|X_n|\\le Y$ almost surely for every n, $\\mathbb{E}Y<\\infty$, then $lim_{n\\to \\infty}EX_n=EX$\n\n对于Borel可测实值函数也一样成立:若$f_n(x)\\le g$ almost surely for every n, and $\\int_{-\\infty}^\\infty g(x)dx<\\infty$\n\n若$f_n(x)\\le g$ almost surely for every n, and $\\int_{-\\infty}^\\infty g(x)dx<\\infty$\n\n$lim_{n\\to \\infty}\\int_{-\\infty}^\\infty f_n(x)dx=\\int_{-\\infty}^\\infty f(x)dx$\n\n## Computation of Expectations\n\n**theorem** $g$ is a Borel measurable function on $\\mathbb{R}$ Then:\n\n$\\mathbb{E} |g(X)|=\\int_\\mathbb{R} |g(x)|d\\mu_X(x)$ , if this quantity is finite, then$\\mathbb{E} g(X)=\\int_\\mathbb{R} g(x)d\\mu_X(x)$\n\nPROOF\n\n1. $\\mathbb{EI}_B(X)=\\mathbb{P}\\{X\\in B\\}=\\mu_X(B)=\\int_\\mathbb{R}\\mathbb{I}_B(x)d\\mu_X(x)$\n2. nonnegative simple functions. A simple function is a finite sum of indicator functions times constants \n \n $$g(x)=\\sum\\alpha_k \\mathbb{I}_{B_k}(x)$$\n \n so \n \n $$\\mathbb{E}g(X)=\\mathbb{E}\\sum \\alpha_k \\mathbb{I}\\_{B\\_k}(X)=\\sum \\alpha_k\\int_R\\mathbb{I}\\_{B\\_k}d\\mu_X(x)=\\int_R(\\sum \\alpha_k\\mathbb{I}\\_{B\\_k}(x))d\\mu_X(x)=\\int_R g(x)d\\mu_X(x)$$\n \n3. when g is nonnegative Borel-measurable functions. \n \n $$B_{k,n}=\\{x;\\frac{k}{2^n}\\le g(x)\\le \\frac{k+1}{2^n}\\},k=0,1,2,\\dots,4^n-1$$\n \n $$g_n(x)=\\sum \\frac{k}{2^n}\\mathbb{I}\\_{B\\_{k,n}}(x)$$\n \n $$\\mathbb{E}g(X)=\\lim \\mathbb{E}g_n(X)=\\lim \\int_R g_n(x)d\\mu_X(x)=\\int_R g(x)d\\mu_X(x)$$\n \n4. when g is general Borel-measurable function.\n \n $g^+(x)=\\max\\{g(x),0\\},g^-(x)\\min\\{-g(x),0\\}$\n \n\n**Theorem** $X$ is a random variable on a probability space $(\\Omega,\\mathcal{F},\\mathbb{P})$, and let g be a Borel measurable function on $\\mathbb{R}$. $X$ has a density $f$ \n\n$\\mathbb{E}|g(X)|=\\int|g(x)|f(x)dx$\n\nif quantity is finite, then \n\n$\\mathbb{E}g(X)=\\int g(x)f(x)dx$\n\nPROOF\n\nsimple functions\n\n$$\\mathbb{E}g(X)=\\mathbb{E}(\\sum \\alpha_k \\mathbb{I}\\_{B\\_k}(X))=\\sum \\alpha_k \\mathbb{E}\\mathbb{I}\\_{B_k}(X)=\\sum \\alpha_k \\int \\mathbb{I}\\_{B\\_k}f(x)dx\\\\\\\\=\\int \\sum \\alpha\n\\_k\\mathbb{I}\\_{B\\_k}(x)f(x)dx=\\int g(x)f(x)dx$$\n\nnonnegative Borel measurable functions\n\n$$\\mathbb{E}g_n(X)=\\int g_n(x)f(x)dx$$\n\n## Change of Measure\n\nWe can use a positive random variable $Z$ to change probability measures on a space $\\Omega$. We need to do this when we change from the actual probability measure $\\mathbb{P}$ to the risk-neutral probability measure $\\widetilde{\\mathbb{P}}$ in models of financial markets.\n\n$$Z(\\omega)\\mathbb{P}(\\omega)=\\widetilde{\\mathbb{P}}(\\omega)$$\n\nto change from $\\mathbb{P}$ to $\\widetilde{\\mathbb{P}}$, we need to reassign probabilities in $\\Omega$ using $Z$ to tell us where in $\\Omega$ we should revise the probability upward and where downward. \n\n*we should do this set-by-set, but not $\\omega$-by-$\\omega$. According to following theorem*\n\n**Theorem** let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space and let $Z$ be an almost surely nonnegative random variable with $\\mathbb{E}Z=1$. for $A\\in\\mathcal{F}$, define $\\widetilde{\\mathbb{P}}(A)=\\int_AZ(\\omega)d\\mathbb{P}(\\omega)$. Then $\\widetilde{\\mathbb{P}}$ is a probability measure. If $X$ is a nonnegative random variable, then$\\widetilde{\\mathbb{E}}X=\\mathbb{E}[XZ]$. If $Z$ is almost surely strictly positive, we also have $\\mathbb{E}Y=\\widetilde{\\mathbb{E}}[\\frac{Y}{Z}]$ for every nonnegative random variable $Y$.\n\nPROOF\n\n$\\widetilde{\\mathbb{P}}(\\Omega)=1$, and countably additive. \n\ncountably additive\n\nlet $A_1,A_2,A_3,\\dots$ be a sequence of disjoint sets in $\\mathcal{F}$, and define $B_n=\\cup_{k=1}^n A_k$\n\nwe can use the monotone convergence theorem, to write\n\n$$\\widetilde{\\mathbb{P}}(\\cup \\_{k=1}^\\infty A\\_k)=\\widetilde{\\mathbb{P}}(B\\_\\infty)=\\int\\_\\Omega \\mathbb{I}\\_{B\\_\\infty}(\\omega)Z(\\omega)d\\mathbb{P}(\\omega)\\\\\\\\=\\lim\\_{n\\to \\infty}\\int\\_\\Omega \\mathbb{I}\\_{B\\_n}(\\omega)Z(\\omega)d\\mathbb{P}(\\omega)\\\\\\\\=\\lim\\_{n\\to \\infty}\\sum\\int\\_\\Omega\\mathbb{I}\\_{A\\_k}(\\omega)Z(\\omega)d\\mathbb{P}(\\omega)=\\sum\\_{k=1}^\\infty\\widetilde{\\mathbb{P}}(A\\_k)$$\n\n**Definition** 如果两个概率测度下sigma代数中零概率的集合相同,那么称两个概率测度为equivalent\n\n在金融中,实际概率测度和风险中性概率测度就是equivalent的,在risk neutral world中almost work的hedge在actual world中一定也almost surely work\n\n**Definition** 对于equivalent的两个概率测度以及它们之间的almost surely positive random variable, 这个随机变量$Z$称之为Radon-Nikodym derivative of$\\widetilde{\\mathbb{P}}$ with respect to $\\mathbb{P}$ and we write $Z=\\frac{d\\widetilde{\\mathbb{P}}}{d\\mathbb{P}}$, $Z$ 的存在性成为Radon-Nikodym Theorem\n\n# Information and Conditioning\n\n## Information and $\\sigma$-algebras\n\nThe hedge must specify what position we will take in the underlying security at each future time contingent on how the uncertainty between the present time and that future time is resolved.\n\n**resolve sets by information**\n\n$\\Omega$ is the set of 8 possible outcomes of 3 coin tosses,\n\n$A_H=\\{HHH,HHT,HTH,HTT\\},A_T=\\{THH,THT,TTH,TTT\\}$\n\nif we are told the first coin toss only. the four sets that are resolved by the first coin toss form the $\\sigma$-algebra\n\n$\\mathcal{F}_1=\\{\\phi,\\Omega,A_H,A_T\\}$\n\nthis $\\sigma$-algebra contains the information learned by observing the first coin toss.\n\n如果某几个集合是resolved,那么他们的并,以及各自的补也是resolved,符合$\\sigma$-algebra\n\n**Definition** let $\\Omega$ be a nonempty set. Let $T$ be a fixed positive number and assume that for each $t\\in [0,T]$ there is a $\\sigma-algebra$ $\\mathcal{F}(t)$. Assume further that if $s\\le t$, then every set in $\\mathcal{F}(s)$ is also in $\\mathcal{F}(t)$. Then we call the collection of $\\sigma-algebra$ $\\mathcal{F}(t)$ a filtration.\n\nAt time $t$ we can know whether the true $\\omega$ lies in a set in $\\mathcal{F}(t)$\n\nLet $\\Omega=C_0[0,T]$, and assign probability to the sets in $\\mathcal{F}=\\mathcal{F}(T)$, then the paths $\\omega\\in C_0[0,T]$ will be the paths of the **Brownian motion**.\n\n**Definition** Let $X$ be a random variable defined on a nonempty sample space $\\Omega$. The $\\sigma-algebra$ generated by $X$, denoted $\\sigma(X)$, is the collection of all subsets of $\\Omega$ of the form $\\{X\\in B\\}$, $B$\n **ranges over** the Borel subsets of $\\mathbb{R}$\n\n这里的区别和简并有点像,随机变量是本征值,Filtration是量子态\n\n**Definition** Let $X$ be a random variable defined on a nonempty sample space $\\Omega$. Let $\\mathcal{G}$ be a $\\sigma-algebra$ of subsets of $\\Omega$. If every set in $\\sigma(X)$ is also in $\\mathcal{G}$, we say that $X$ is $\\mathcal{G}-measurable$\n\n意味着$\\mathcal{G}$ 中的信息足够决定$X$ 的值。对于borel可测函数$f$,$f(X)$也是$\\mathcal{G}-measurable$的。对于多元函数同样成立\n\n**Definition** Let $\\Omega$ be a nonempty sample space equipped with a filtration $\\mathcal{F}(t)$. Let \n\n$X(t)$ be a collection of random variables indexed by $t\\in [0,T]$, We say this collection of random variables is an adapted stochastic process if, for each $t$, the random variable $X(t)$ is $\\mathcal{F}(t)-measurable$ \n\n## Independence\n\n对于一个随机变量和一个$\\sigma-algebra$ $\\mathcal{G}$, measurable 和 independent 是两种极端,但大部分情况下,$\\mathcal{G}$中但信息可以估计$X$, 但不足以确定$X$的值。\n\nIndependence会受到概率度量的影响,但measurability不会。\n\nprobability space $(\\Omega,\\mathcal{F},\\mathbb{P})$,$\\mathcal{G}\\in \\mathcal{F}, \\mathcal{H}\\in \\mathcal{F}$, $\\Omega$ 中的两个$\\sigma-algebra$$A$和$B$独立如果$\\mathbb{P}(A\\cap B)=\\mathbb{P}(A)\\cdot\\mathbb{P}(B)$, for all $A\\in \\mathcal{G},B\\in \\mathcal{H}$\n\n独立的定义可以拓展到随机变量($\\sigma-algebra$ they generate are independent)之间,随机变量与$\\sigma-algebra$之间。\n\n**Definition** $(\\Omega,\\mathcal{F},\\mathbb{P})$ is a probability space and let $\\mathcal{G}_1,\\mathcal{G}_2,\\mathcal{G}_3\\dots$ be a sequence of $sub-\\sigma-algebra$ of $\\mathcal{F}$. For a fixed positive integer n, we say that the n $\\sigma-algebra$s $\\mathcal{G}_1,\\mathcal{G}_2,\\mathcal{G}_3\\dots\\mathcal{G}_n$ are independent if$\\mathbb{P}(A_1\\cap A_2\\cap \\dots\\cap A_n)=\\mathbb{P}\n(A_1)\\mathbb{P}\n(A_2)\\dots \\mathbb{P}\n(A_n)$ for all $A_i\\in \\mathcal{G}_i$\n\n这个同样也可以拓展到随机变量之间以及随机变量与$\\sigma-algebra$之间。\n\n**Theorem** Let $X$ and $Y$ be independent random variables, and let $f$ and $g$ be Borel measurable functions on $\\mathbb{R}$. Then$f(X)$ and $g(Y)$ are independent random variables.\n\nPROOF\n\nLet $A$ be in the $\\sigma-algebra$ generated by $f(X)$. This $\\sigma-algebra$ is a $sub-\\sigma -algebra$ of $\\sigma(X)$. \n\n这很自然,every set in $A$ is of the form$\\{\\omega \\in \\Omega;f(X(\\omega))\\in C\\}\\text{,where }C\\text{ is a Borel subset of }\\mathbb{R}$. 只需要定义$D=\\{x\\in \\mathbb{R};f(x)\\in C\\}$. Then we know$A\\in \\sigma(X)$. Let $B$ be the $\\sigma-algebra$ gnenerated by $g(Y)$, then $B\\in \\sigma(Y)$. 由于$X,Y$独立,所以$A,B$独立。\n\n**Definition** Let$X$ and $Y$ be random variables. The pair of random variables$(X,Y)$ takes values in the plane$\\mathbb{R}^2$, and the joint distribution measure of $(X,Y)$ is given by$\\mu_{X,Y}(C)=\\mathbb{P}\\{(X,Y)\\in C\\}$ for all Borel sets $C\\in \\mathbb{R}^2$\n\n同样满足概率度量的两个条件:全空间测度为1,以及countable additivity preperty\n\n**Theorem** Let $X$ and $Y$ be random variables. The following conditions and equivalent.\n\n1. $X$ and $Y$ are independent\n2. the joint distribution measure factors:\n \n $\\mu_{X,Y}(A\\times B)=\\mu_X(A)\\mu_Y(B)$ for all Borel subsets$A\\in \\mathbb{R},B\\in\\mathbb{R}$\n \n3. the joint cumulative distribution function factors\n \n $F_{X,Y}(a,b)=F_X(a)F_Y(b)$ for all $a\\in \\mathbb{R},b\\in \\mathbb{R}$\n \n4. the joint moment-generating function factor:(矩母函数)\n \n $\\mathbb{E}e^{uX+vY}=\\mathbb{E}e^{uX}\\cdot\\mathbb{E}e^{vY}$\n \n5. the joint density factors(if there is one)\n \n $f_{X,Y}(x,y)=f_X(x)f_Y(y)$ for almost every$x\\in\\mathbb{R},y\\in\\mathbb{R}$\n \n\nconditions above imply but are not equivalent to:\n\n1. $\\mathbb{E}[XY]=\\mathbb{E}X\\cdot\\mathbb{E}Y$ provided $\\mathbb{E}|XY|<\\infty$\n\n**Definition** Let $X$ be a random variable whose expected value is defined. The variance of $X$, denoted $Var(X)$ is $Var(X)=\\mathbb{E}[(X-\\mathbb{E}X)^2]=\\mathbb{E}[X^2]-(\\mathbb{E}X)^2$\n\ncovariance of $X$ and $Y$ is $Cov(X,Y)=\\mathbb{E}[(X-\\mathbb{E}X)(Y-\\mathbb{E}Y)]=\\mathbb{E}[XY]-\\mathbb{E}X\\cdot\\mathbb{E}Y$\n\ncorrelation coefficient of $X$and $Y$ is $\\rho(X,Y)=\\frac{Cov(X,Y)}{\\sqrt{Var(X)Var(Y)}}$\n\nif $\\rho(X,Y)=0$, we say that $X$ and $Y$ are uncorrelated\n\n## General Conditional Expectations\n\n**Definition** Let$(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space, let $\\mathcal{G}$ be a sub-$\\sigma$-algebra of $\\mathcal{F}$, and let $X$ be a random variable that is either nonnegative or integrable. The conditional expectation of $X$ given $\\mathcal{G}$, denoted$\\mathbb{E}[X|\\mathcal{G}]$, is any random variable that satisfies\n\n1. **Measurability $\\mathbb{E}[X|\\mathcal{G}]$** is $\\mathcal{G}$ measurable\n2. **Partial averaging $\\int_A\\mathbb{E}[X|\\mathcal{G}(\\omega)]=\\int_AX(\\omega)d\\mathbb{P}(\\omega)$** for all $A\\in \\mathcal{G}$\n\nIf $\\mathcal{G}$ is generated by some other random variable $W$, then we can write$\\mathbb{E}[X|W]$\n\n(1) means although the estimate of $X$based on the information in $\\mathcal{G}$ is itself a random variable, the value of the estimate $\\mathbb{E}[X|\\mathcal{G}]$ can be determined from the information in $\\mathcal{G}$\n\n存在性可以由Radon-Nikodym Theorem证明\n\n唯一性的证明如下:If $Y$ and $Z$ both satisfy conditions, then their difference $Y-Z$ is as well, and thus the set $A=\\{Y-Z>0\\}$ is in $\\mathcal{G}$. 根据(2),$\\int_AY(\\omega)d\\mathbb{P}(\\omega)=\\int_AX(\\omega)d\\mathbb{P}(\\omega)=\\int_AZ(\\omega)d\\mathbb{P}(\\omega)$\n\nHence $Y=Z$ almost surely.\n\n**Theorem** Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space and let $\\mathcal{G}$ be a sub-$\\sigma$-algebra of $\\mathcal{F}$\n\n1. linearity of conditional expectations\n$\\mathbb{E}[c_1X+c_2Y|\\mathcal{G}]=c_1\\mathbb{E}[X|\\mathcal{G}]+c_2\\mathbb{E}[Y|\\mathcal{G}]$\n2. taking out what is known. \n \n If $X$ is $\\mathcal{G}$-measurable\n \n $\\mathbb{E}[XY|\\mathcal{G}]=X\\mathbb{E}[Y|\\mathcal{G}]$\n \n3. iterated conditioning.\n \n If $\\mathcal{H}$ is a sub-$\\sigma$-algebra of $\\mathcal{G}$ and $X$ is an integrable random variable, then\n \n $\\mathbb{E}[\\mathbb{E}[X|\\mathcal{G}]|\\mathcal{H}]=\\mathbb{E}[X|\\mathcal{H}]$\n \n4. independence\n \n If $X$ is independent of $\\mathcal{G}$, then $\\mathbb{E}[X|\\mathcal{G}]=\\mathbb{E}X$\n \n5. conditional Jensen’s inequality\n \n $\\mathbb{E}[\\phi(X)|\\mathcal{G}]\\ge\\phi(\\mathbb{E}[X|\\mathcal{G}])$\n \n\n**Lemma** Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space, and let $\\mathcal{G}$ be a sub-$\\sigma$-algebra of $\\mathcal{F}$. Suppose the random variables $X_1,\\dots,X_K$ are $\\mathcal{G}$-measurable and the random variables$Y_1,\\dots,Y_L$ are independent of $\\mathcal{G}$. Let $f(x_1,\\dots,x_K,y_1,\\dots,y_L)$ be a function of the dummy variables, and define: \n\n$g(x_1,\\dots,x_K)=\\mathbb{E}f(x1,\\dots,x_K,Y_1,\\dots,Y_L)$\n\nThis means holding $X_i$ constant and integrate out $Y_i$.\n\nThen,$\\mathbb{E}[f(X_1,\\dots,X_K,Y_1,\\dots,Y_L)|\\mathcal{G}]=g(X_1,\\dots,X_K)$\n\n**Definition** Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space, let $T$ be a fixed positive number, and let $\\mathcal{F}(t)$, $0\\le t\\le T$, be a filtration of $sub-\\sigma-algebra$ of $\\mathcal{F}$. Consider an adapted stochastic process $M(t)$:\n\n1. If $\\mathbb{E}[M(t)|\\mathcal{F}(s)]=M(s)$ for all $0\\le s\\le t \\le T$, this process is a ***martingale***. It has no tendency to rise or fall.\n2. If $\\mathbb{E}[M(t)|\\mathcal{F}(s)]\\le M(s)$ for all $0\\le s\\le t \\le T$, this process is a ***supermartingale***. It has no tendency to rise, it may have a tendency to fall.\n3. If $\\mathbb{E}[M(t)|\\mathcal{F}(s)]\\ge M(s)$ for all $0\\le s\\le t \\le T$, this process is a ***submartingale***. It has no tendency to fall, it may have a tendency to rise.\n\n**Definition** Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space, let $T$ be a fixed positive number, and let $\\mathcal{F}(t)$, $0\\le t\\le T$, be a filtration of $sub-\\sigma-algebra$ of $\\mathcal{F}$. Consider an adapted stochastic process $X(t)$. Assume that for all $0\\le s\\le t\\le T$ and for every nonnegative, Borel-measuable function $f$, there is another Borel-measuable function $g$ such that:\n\n$\\mathbb{E}[f(X(t))|\\mathcal{F}(s)]=g(X(s))$\n\nThen we say that the X is a Markov process\n\n# Brownian Motion\n\n## Scaled Random Walks\n\n### Symmetric Random Walk\n\nTo build a **symmetric random walk** we repeatedly toss a fair coin.\n\n$X_j=\\begin{cases}1 \\text{ if }\\omega_j=H\\\\\\\\-1\\text{ if }\\omega_j=T\\end{cases}$\n\n$M_0=0$, $M_k=\\sum_{j=1}^kX_j$\n\nthe process $M_k$ is a *symmetric random walk.*\n\n### Increments of the Symmetric Random Walk\n\nA random walk has independent increments(独立增量性)\n\nif we choose nonnegative integers$0=k_0<k_1<\\cdots<k_m$ , the random variables $M_{k_i}-M_{k_{i-1}}$ are independent.\n\nEach of these random variables $M_{k_i}-M_{k_{i-1}}=\\sum_{j=k_{i+1}}^{k_{i+1}}X_j$ is called an increment of the random walk. \n\nEach increment has expected value 0 and variance $k_{i+1}-k_i$ . The variance is obvious because $X_j$ are independent.\n\n### Martingale Property for the Symmetric Random Walk\n\nWe choose nonnegative integers $k<l$ and compute:\n\n$\\mathbb{E}[M_l|\\mathcal{F}_k]=\\mathbb{E}[(M_l-M_k)+M_k|\\mathcal{F}_k]=\\mathbb{E}[M_l-M_k|\\mathcal{F}_k]+\\mathbb{E}[M_k|\\mathcal{F}_k]=M_k$\n\n### Quadratic Variation of the Symmetric Random Walk\n\nthe quadratic variation up to time $k$ is defined to be $[M,M]_k=\\sum\\_{j=1}^k(M\\_j-M\\_{j-1})^2=k$\n\nThis is computed path-by-path. taking all the one step increments $M_j-M_{j-1}$ along that path, squaring these increments, and then summing them.\n\nNote that $[M,M]_k$ is the same as $Var(M_k)$, but the computations of these two quantities are quite different. $Var$ is computed by taking an average over all paths, taking their probability into account. If the random walk is not symmetric, the probability distribution would affect $Var$. On the contrary, the probability up and down do not affect the quadratic variation computation.\n\n### Scaled Symmetric Random Walk\n\nWe fix a positive integer $n$ and define the **scaled symmetric random walk** $W^{(n)}(t)=\\frac{1}{\\sqrt{n}}M_{nt}$. If $nt$ is not an integer, we define $W^{(n)}(t)$ by linear interpolation between its values at the nearest points $s$ and $u$ to the left and right of $t$ for which $ns$ and $nu$ are integers. \n\nA Brownian motion is a scaled symmetric random walk with $n\\to \\infty$\n\n$\\mathbb{E}(W^{(n)}(t)-W^{(n)}(s))=0,Var(W^{(n)}(t)-W^{(n)}(s))=t-s$\n\nLet $0\\le s\\le t$ be given, and decompose $W^{(n)}(t)$ as: $W^{(n)}(t)=(W^{(n)}(t)-W^{(n)}(s))+W^{(n)}(s)$ \n\n$(W^{(n)}(t)-W^{(n)}(s))$ is independent of $\\mathcal{F}(s)$, the $\\sigma-algebra$ of information available at time s, and $W^{(n)}(s)$ is $\\mathcal{F}(s)$ measurable. So $\\mathbb{E}[W^{(n)}(t)|\\mathcal{F}(s)]=W^{(n)}(s)$\n\nThe **quadratic variation** of the scaled random walk: \n\n$\\[W^{(n)},W^{(n)}\\]\\(t\\)=\\sum\\_{j=1}^{nt}[W^{(n)}(\\frac{j}{n})-W^{(n)}(\\frac{j-1}{n})]^2=\\sum\\_{j=1}^{nt}[W^{(n)}[\\frac{1}{\\sqrt{n}}X_j]^2=\\sum\\_{j=1}^{nt}\\frac{1}{n}=t$\n\n### Limiting Distribution of the Scaled Random Walk\n\n**Theorem: Central limit** Fix $t\\ge 0$. As $n\\to \\infty$, the distribution of the scaled random walk $W^{(n)}(t)$ evaluated at time $t$ converges to the normal distribution with mean zero and variance $t$.\n\nPROOF\n\nFor the normal density $f(s)=\\frac{1}{\\sqrt{2\\pi t}}e^{-\\frac{x^2}{2t}}$, the moment-generating function is \n\n$\\phi(u)=\\frac{1}{\\sqrt{2\\pi t}}\\int_{-\\infty}^\\infty \\exp\\{ux-\\frac{x^2}{2t}\\}dx=e^{\\frac{1}{2}u^2t}$\n\nIf $t$ is such that $nt$ is an integer, then the moment-generating function for $W^{(n)}(t)$ is:\n\n$\\phi_n(u)=\\mathbb{E}e^{uW^{(n)}(t)}=\\mathbb{E}\\exp\\{\\frac{u}{\\sqrt{n}}M_{nt}\\}=\\mathbb{E}\\exp\\{\\frac{u}{\\sqrt{n}}\\sum_{j=1}^{nt}X_j\\}=\\mathbb{E}\\prod_{j=1}^{nt}\\exp\\{\\frac{u}{\\sqrt{n}}X_j\\}\\\\\\\\=\\prod_{j=1}^{nt}\\mathbb{E}\\exp\\{\\frac{u}{\\sqrt{n}}X_j\\}=\\prod_{j=1}^{nt}(\\frac{e^{\\frac{u}{\\sqrt{n}}}+e^{\\frac{-u}{\\sqrt{n}}}}{2})=(\\frac{e^{\\frac{u}{\\sqrt{n}}}+e^{\\frac{-u}{\\sqrt{n}}}}{2})^{nt}$\n\nwhen $n\\to \\infty$ , $\\phi(u)=e^{\\frac{1}{2}u^2t}$\n\n### Log-Normal Distribution as the Limit of the Binomial Model\n\nWe build a model for a stock price on the time interval from $0$ to $t$ by choosing an integer $n$ and constructing a binomial model for the stock price that takes $n$ steps per unit time. Up factor $u_n=1+\\frac{\\sigma}{\\sqrt{n}}$, down factor $u_d=1-\\frac{\\sigma}{\\sqrt{n}}$. $r=0.$\n\nThe risk-neutral probabilities are then:\n\n$\\tilde{p}=\\frac{1+r-d_n}{u_n-d_n}=\\frac{1}{2}$, $\\tilde{q}=\\frac{u_n-1-r}{u_n-d_n}=\\frac{\\sigma/\\sqrt{n}}{2\\sigma/\\sqrt{n}}=\\frac{1}{2}$\n\nRandom walk $M_{nt}=H_{nt}-T_{nt}$, while $nt=H_{nt}+T_{nt}$\n\nthe stock price at time $t$ is $S_n(t)=S(0)u_n^{H_{nt}}d_n^{T_{nt}}=S(0)(1+\\frac{\\sigma}{\\sqrt{n}})^{\\frac{1}{2}(nt+M_{nt})}(1+\\frac{\\sigma}{\\sqrt{n}})^{\\frac{1}{2}(nt+M_{nt})}(1-\\frac{\\sigma}{\\sqrt{n}})^{\\frac{1}{2}(nt-M_{nt})}$\n\nwe need to identify the distribution of this random variable as $n\\to \\infty$\n\n**Theorem** As $n\\to \\infty$ , the distribution of $S_n(t)$ converges to the distribution of\n\n$S(t)=S(0)\\exp\\{\\sigma W(t)-\\frac{1}{2}\\sigma^2t\\}$ \n\n$W(t)$ is a normal random variable with mean zero and variance $t$\n\nPROOF:\n\n$\\log S_n(t)\\\\\\\\=\\log S(0)+\\frac{1}{2}(nt+M_{nt})\\log (1+\\frac{\\sigma}{\\sqrt{n}})+\\frac{1}{2}(nt-M_{nt})\\log (1-\\frac{\\sigma}{\\sqrt{n}})\\\\\\\\=\\log S(0)+\\frac{1}{2}(nt+M_{nt})(\\frac{\\sigma}{\\sqrt{n}}-\\frac{\\sigma^2}{2n}+O(n^{-3/2}))+\\frac{1}{2}(nt-M_{nt})(\\frac{\\sigma}{-\\sqrt{n}}-\\frac{\\sigma^2}{2n}+O(n^{-3/2}))\\\\\\\\=\\log S(0)+nt(-\\frac{\\sigma^2}{2n}+O(n^{-3/2}))+M_{nt}(\\frac{\\sigma}{\\sqrt{n}}+O(n^{-3/2}))=\\log S(0)-\\frac{1}{2}\\sigma^2t+\\sigma W^{(n)}(t)$\n\nBy the **Central Limit Theorem,** we know that $\\frac{1}{\\sqrt{n}}M_{nt}=W^{(n)}(t)\\to W(t), \\text{when }n\\to \\infty$\n\n## Brownian Motion\n\n### Definition of Brownian Motion\n\n**Definition** Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space. For each $\\omega\\in\\Omega$, suppose there is a continuous function $W(t)$ of $t\\ge 0$ that satisfies $W(0)=0$ that depends on $\\omega$. Then $W(t),t\\ge 0$ is a Brownian motion if for all $t_i$ the increments $W(t_i)-W(t_{i-1})$ are independent and each of these increments is normally distributed with $\\mathbb{E}[W(t_{i+1})-W(t_i)]=0,Var[W(t_{i+1})-W(t_i)]=t_{i+1}-t_i$\n\nDifference between BM and a scaled random walk: the scaled random walk has a natural time step and is linear between these time steps, whereas the BM has no linear pieces.\n\n### Distribution of Brownian Motion\n\nFor any two times, the covariance of $W(s)$ and $W(t)$ for $s\\le t$ is\n\n$\\mathbb{E}[W(s)W(t)]=\\mathbb{E}[W(s)(W(t)-W(s))+W^2(s)]=\\mathbb{E}[W(s)]\\mathbb{E}[(W(t)-W(s))]+\\mathbb{E}[W^2(s)]=s$\n\nWe compute the moment-generating function of the random vector$(W(t_1),W(t_2),\\dots,W(t_m))$\n\n$\\phi=\\mathbb{E}\\exp\\{u_mW(t_m)+\\dots+u_1W(t_1)\\}=\\mathbb{E}\\exp\\{u_m(W(t_m)-W(t_{m-1}))+\\dots+(u_1+u_2+\\dots+u_m)W(t_1)\\}=\\mathbb{E}\\exp\\{u_m(W(t_m)-W(t_{m-1}))\\}\\cdots \\mathbb{E}\\exp\\{(u_1+u_2+\\cdots+u_m)W(t_1)\\}=\\exp\\{\\frac{1}{2}u_m^2(t_m-t_{m-1})\\}\\cdots\\exp\\{(u_1+u_2+\\cdots+u_m)^2t_1\\}$\n\nThe distribution of the Brownian increments can be specified by specifying the joint density or the joint moment-generating function of the random variables\n\n**Theorem** Let$(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space. For each $\\omega\\in\\Omega$, suppose there is a continuous function $W(t)$ of $t\\ge 0$ that satisfies $W(0)=0$ and that depends on $\\omega$. \n\n1. For all $0< t_0< t_1\\cdots <t_m$, the increments are independent and each of these increments is normally distributed with mean and variance given by$\\mathbb{E}[W(t_{i+1})-W(t_i)]=0,Var[W(t_{i+1})-W(t_i)]=t_{i+1}-t_i$\n2. For all $0< t_0< t_1\\cdots <t_m$, the random variables $W(t_i)$ are jointly normally distributed with means equal to zero and covariance matrix\n \n $\\begin{pmatrix} t_{1} &t_1 \\cdots & t_{1} \\\\\\\\ t_1&t_2\\cdots &t_2\\\\\\\\ \\vdots & \\ddots & \\vdots \\\\\\\\ t_{1} &t_2 \\cdots & t_{m} \\end{pmatrix}$ \n \n3. the random variables have the joint moment-generating function mentioned before\n\n### Filtration for Brownian Motion\n\n**Definition** Let$(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space on which is defined a Brownian motion $W(t),t\\ge 0$. A filtration for the Brownian motion is a collection of $\\sigma$-algebra $\\mathcal{F}(t),t\\ge 0$, satisfying:\n\n1. **Information accumulates**\n2. **Adaptivity: $W(t)$** is **$\\mathcal{F}(t)$**-measurable\n3. **Independence of future increments**\n\n$\\Delta(t),t\\ge0$, be a stochastic process. $\\Delta(t)$ is adapted to the filtration $\\mathcal{F}(t)$ if for each $t\\ge 0$ the random variable $\\Delta(t)$ if $\\mathcal{F}(t)$-measurable.\n\nThere are two possibilities for the filtration $\\mathcal{F}(t)$ for a Brownian motion. \n\n1. to let $\\mathcal{F}(t)$ contain only the info obtained by observing the BM itself up to time $t$. \n2. to include in $\\mathcal{F}(t)$ info obtained by observing the BM and one or more other processes. But if the info in $\\mathcal{F}(t)$ includes observations of processes other than the BM $W$, this additional info is not allowed to give clues about the future increments because of property iii\n\n### Martingale Property for Brownian Motion\n\n**Theorem** Brownian motion is a martingale\n\n## Quadratic Variation\n\nFor BM, there is no natural step size. If we are given $T>0$, we could simply choose a step size, say $\\frac{T}{n}$ for some large $n$, and compute the quadratic variation up to time $T$ with this step size:\n\n$\\sum_{j=0}^{n-1}[W(\\frac{(j+1)T}{n})-W(\\frac{jT}{n})]^2$\n\nThe variation of paths of BM is not zero, which makes stochastic calculus different from ordinary calculus\n\n### First-Order Variation\n\n$FV_T(f)=|f(t_1)-f(0)|+|f(t_2)-f(t_1)|+\\dots+|f(T)-f(t_2)|=\\int_0^{t_1}f'(t)dt+\\dots+\\int_{t_2}^Tf'(t)dt=\\int_0^T|f'(t)|dt$\n\nWe first choose a partition $\\Pi=\\{t_0,t_1,\\dots,t_n\\}$ of $[0,T]$, which is a set of times. These will serve to determine the step size. The maximum step size of the partition will be denoted $\\Vert\\Pi\\Vert=\\max_{j=0,\\dots,n-1}(t_{j+1}-t_j)$. We then define:\n\n$FV_T(f)=\\lim_{\\Vert\\Pi\\Vert\\to0}\\sum_{j=0}^{n-1}\\vert f(t_{j+1})-f(t_j)\\vert$\n\n用中值定理可以证明与积分相等\n\n### Quadratic Variation\n\n**Definition** Let $f(t)$ be a function defined for $0\\le t\\le T$. The quadratic variation to $f$ up to time $T$ is \n\n$[f,f]\\(T\\)=\\lim\\_{\\Vert\\Pi\\Vert\\to0}\\sum\\_{j=0}^{n-1}\\vert f(t\\_{j+1})-f(t\\_j)\\vert$\n\nif $f$ is derivative, then $[f,f](T)=0$\n\nif $\\int_0^T\\vert f'(t^*_j)\\vert ^2dt$ is infinite, then $[f,f]\\(T\\)$ lead to a $0\\cdot\\infty$ situation, which can be anything between $0$ and $\\infty$\n\n**Theorem** Let $W$ be a Brownian motion. Then $[W,W]\\(T\\)=T$ for all $T\\ge 0$ almost surely.\n\nPROOF\n\nDefine the *sample quadratic variation* corresponding to the partition of $[0,T]$, $\\Pi =\\{t_0,t_1,\\dots,t_n\\}$ to be\n\n $Q_\\Pi=\\sum_{j=0}^{n-1}(W(t_{j+1})-W(t_j))^2$\n\nWe can show that $Q_\\Pi$ converges to $T$ as $\\Vert\\Pi\\Vert\\to0$\n\n$\\mathbb{E}[(W(t_{j+1})-W(t_j))^2]=Var[W(t_{j+1})-W(t_j)]=t_{j+1}-t_j$ implies:\n\n$\\mathbb{E}Q_\\Pi=\\sum\\mathbb{E}[(W(t_{j+1})-W(t_j))^2]=\\sum(t_{j+1}-t_j)=T$\n\n$Var[(W(t_{j+1})-W(t_j))^2]=\\mathbb{E}[(W(t_{j+1})-W(t_j))^4]-2(t_{j+1}-t_j)\\mathbb{E}[(W(t_{j+1})-W(t_j))^2]+(t_{j+1}-t_j)^2$\n\n$\\mathbb{E}[(W(t_{j+1})-W(t_j))^4]=3(t_{j+1}-t_j)^2$,$\\mathbb{E}[(W(t_{j+1})-W(t_j))^2]=t_{j+1}-t_j$\n\nPROOF\n\nBy Ito’s formula, we have\n\n$𝑊^4(t)=4\\int^𝑡_0𝑊^3_s𝑑𝑊_s+6\\int^𝑡_0𝑊^2_sds$\n\n$M(t):=\\int_0^tW_s^3dW_s=0$ is a martingale and $\\mathbb{E}M(t)=\\mathbb{E}M(0)=0$\n\n$\\mathbb{E}W^4(t)=6\\int_0^t\\mathbb{E}[W_s^2]ds=6\\int_0^tsds=3t^2$\n\nso $Var[(W(t_{j+1}-W(t_j))^4]=2(t_{j+1}-t_j)^2$\n\nand $Var(Q_\\Pi)=\\sum 2(t_{j+1}-t_j)^2\\le2\\Vert\\Pi\\Vert T$\n\nIn particular, $\\lim_{\\Vert\\Pi\\Vert\\to 0}Var(Q_\\Pi)=0,lim_{\\Vert\\Pi\\Vert\\to0}Q_\\Pi=\\mathbb{E}Q_\\Pi=T$\n\n$(W(t_{j+1})-W(t_j))^2\\approx t_{j+1}-t_j$$(W(t_{j+1})-W(t_j))^2=t_{j+1}-t_j$ when $t_{j+1}-t_j$ is very small\n\n$dW(t)dW(t)=dt$ is the informal write\n\n$dWdt=0,dtdt=0$\n\n### Volatility of Geometric Brownian Motion\n\ngeometric Brownian motion: $S(t)=S(0)\\exp\\{\\sigma W(t)+(\\alpha-\\frac{1}{2}\\sigma^2)t\\}$\n\nrealized volatility: the sum of the squares of the log returns\n\nfor $T_1=t_0<t_1<\\cdots<tm=T_2$,\n\n$\\sum (\\log\\frac{S(t_{j+1})}{S(t_j)})^2=\\sigma^2\\sum(W(t_{j+1})-W(t_j))^2+(\\alpha-\\frac{1}{2}\\sigma^2)^2\\sum(t_{j+1}-t_j)^2+2\\sigma (\\alpha-\\frac{1}{2}\\sigma^2)\\sum(W(t_{j+1})-W(t_j))(t_{j+1}-t_j)$\n\nWhen the maximum step size $\\Vert\\Pi\\Vert=\\max_{j=0,1,\\dots,m-1}(t_{j+1}-t_j)$ is small, then the first term is approximately equal to its limit $\\sigma^2(T_2-T_1)$,hence, we have:\n\n$\\frac{1}{T_2-T_1}\\sum(\\log\\frac{S(t_{j+1})}{S(t_j)})^2\\approx\\sigma^2$\n\n## Markov Property\n\n**Theorem** Let$W(t),t\\ge0$, be a Brownian motion and let $\\mathcal{F}(t),t\\ge0$ Be a filtration for this Brownian motion. Then $W(t)$ is a Markov process\n\nPROOF\n\nWe need to show: $\\mathbb{E}[f(W(t))\\vert \\mathcal{F}(s)]=g(W(s))$ $g$ Exists whenever given $0\\le s\\le t,f$\n\n$\\mathbb{E}[f(W(t))\\vert\\mathcal{F}(s)]=\\mathbb{E}[f((W(t)-W(s))+W(s))\\vert\\mathcal{F}(s)]$\n\n$W(t)-W(s)$ is normally distributed with mean zero and variance $t-s$\n\nReplace $W(s)$ with a dummy variable $x$\n, define $g(x)=\\mathbb{E}f(W(t)-W(s)+x)$, then \n\n$g(x)=\\frac{1}{\\sqrt{2\\pi(t-s)}}\\int f(w+x)\\exp\\{-\\frac{w^2}{2(t-s)}\\}dw=\\frac{1}{\\sqrt{2\\pi\\tau}}\\int f(y)\\exp\\{-\\frac{(y-x)^2}{2\\tau}\\}dy$\n\nDefine the *transition density $p(\\tau,x,y):=\\frac{1}{\\sqrt{2\\pi\\tau}}e^{-\\frac{(y-x)^2}{2\\tau}},\\tau=t-s$*\n\n$g(x)=\\int f(y)p(\\tau,x,y)dy$ \n\nAnd $\\mathbb{E}[f(W(t))\\vert\\mathcal{F}(s)]=\\int f(y)p(\\tau,W(s),y)dy$\n\nConditioned on the information in $\\mathcal{F}(s)$, the conditional density of $W(t)$ is $p(\\tau,W(s),y)$. This is a density in the variable $y$, normal with mean $W(s)$ and variance $\\tau$. The only information from $\\mathcal{F}(s)$ that is relevant is the value of $W(s)$\n\n## First Passage Time Distribution\n\nexponential martingale corresponding to $\\sigma$: $Z(t)=\\exp\\{\\sigma W(t)-\\frac{1}{2}\\sigma^2t\\}$\n\n**Theorem** Exponential martingale Let $W(t),t\\ge 0$, be a Brownian motion with a filtration $\\mathcal{F}(t),t\\ge 0$, and let $\\sigma$ be a constant, thew process $Z(t)$ is a martingale\n\nPROOF\n\n$\\mathbb{E}[Z(t)\\vert\\mathcal{F}(s)]=\\mathbb{E}[\\exp\\{\\sigma W(t)-\\frac{1}{2}\\sigma^2t\\}\\vert \\mathcal{F}(s)]=\\mathbb{E}[\\exp\\{\\sigma (W(t)-W(s))\\}\\cdot\\exp\\{\\sigma W(s)-\\frac{1}{2}\\sigma^2t\\}\\vert \\mathcal{F}(s)]=\\exp\\{\\sigma W(s)-\\frac{1}{2}\\sigma^2t\\}\\cdot\\mathbb{E}[\\exp\\{\\sigma (W(t)-W(s))\\}]$\n\n$W(t)-W(s)$ is a normal distribution with mean zero and variance $\\sigma$ so $\\mathbb{E}[\\exp\\{\\sigma (W(t)-W(s))\\}]=\\frac{1}{2}\\sigma^2(t-s)$\n\n$\\mathbb{E}[Z(t)\\vert\\mathcal{F}(s)]=Z(s)$\n\nLet $m$ be a real number, and define the first passage time to level $m$: $\\tau_m=\\min\\{t\\ge 0;W(t)=m\\}$ if the BM never reaches the level $m$, we set $\\tau_m=\\infty$. A martingale that is stopped at a stopping time is still martingale and thus must have constant expectation. So:\n\n$1=Z(0)=\\mathbb{E}Z(t\\land\\tau_m)=\\mathbb{E}[\\exp\\{\\sigma W(t\\land\\tau_m)-\\frac{1}{2}\\sigma^2(t\\land\\tau_m)\\}]$ $t\\land\\tau_m$ means the minimum of $t$ and $\\tau_m$\n\nIf $\\tau_m<\\infty$, the term $\\exp\\{-\\frac{1}{2}\\sigma^2(t\\land\\tau_m)\\}$ is equal to $\\exp\\{-\\frac{1}{2}\\sigma^2\\tau_m\\}$ for large enough $t$. $\\tau_m=\\infty$, the result converges to zero. So: \n\n$\\lim\\_{t\\to\\infty\\}\\exp\\{\\sigma W\\(t\\land\\tau_m\\)-\\frac{1}{2}\\sigma^2(t\\land\\tau_m)\\}=\\mathbb{I}_\\{\\{\\tau_m<\\infty\\}}\\exp\\{\\sigma m-\\frac{1}{2}\\sigma^2\\tau_m\\\\}$\n\nnow we can obtain:\n\n$1=\\mathbb{E}[\\mathbb{I}_{\\{\\tau_m<\\infty\\}}\\exp\\{\\sigma m-\\frac{1}{2}\\sigma^2\\tau_m\\}]$\n\n$\\mathbb{E}[\\mathbb{I}_{\\{\\tau_m<\\infty\\}}\\exp\\{-\\frac{1}{2}\\sigma^2\\tau_m\\}]=e^{-\\sigma m}$\n\nwhen $\\sigma\\to0$, we get $\\mathbb{P}\\{\\tau_m<\\infty\\}=1$\n\n$\\tau_m$ is finite almost surely, so we may drop the indicator to obtain:\n\n$\\mathbb{E}[\\exp\\{-\\frac{1}{2}\\sigma^2\\tau_m\\}]=e^{-\\sigma m}$\n\n**Theorem** For $m\\in \\mathbb{R}$, the first passage time of Brownian motion to level $m$ is finite almost surely, and the Laplace transform of its distribution is given by \n\n$\\mathbb{E}e^{-\\alpha \\tau_m}=e^{-\\vert m \\vert\\sqrt{2\\alpha}}$ for all $\\alpha>0$\n\ndifferentiation: $\\mathbb{E}[\\tau_me^{-\\alpha\\tau_m}]=\\frac{\\vert m\\vert}{\\sqrt{2\\alpha}}e^{-\\vert m\\vert\\sqrt{2\\alpha}}$ for all $\\alpha>0$\n\nlet $\\alpha\\to 0$ get obtain $\\mathbb{E}\\tau_m=\\infty$ so long as $m\\neq0$\n\n## Reflection Principle\n\n### Reflection Equality\n\nfor each Brownian motion path that reaches level m prior to time t but is at a level w below m at time t, there is a \"reflected path\" that is at level $2m-w$ at time $t$. This reflected path is constructed by switching the up and down moves of the Brownian motion from time $\\tau_m$onward.\n\n**Reflection equality**\n\n$\\mathbb{P}\\{\\tau_m\\le t,W(t)\\le w\\}=\\mathbb{P}\\{W(t)\\ge 2m-w\\},w\\le m,m>0$\n\n### First Passage Time Distribution\n\n**Theorem** For all $m\\neq0$, the random variable $\\tau_m$ has cumulative distribution function:\n\n$\\mathbb{P}\\{\\tau_m\\le t\\}=\\frac{2}{\\sqrt{2\\pi}}\\int_{\\frac{\\vert m\\vert}{\\sqrt{t}}}^\\infty e^{-\\frac{y^2}{2}}dy$\n\n$f_{\\tau_m}(t)=\\frac{d}{dt}\\mathbb{P}=\\frac{\\vert m\\vert}{t\\sqrt{2\\pi t}}e^{-\\frac{m^2}{2t}}$\n\nPROOF\n\nUse the reflection equality, we obtain\n\n$\\mathbb{P}\\{\\tau_m\\le t,W(t)\\le m\\}=\\mathbb{P}\\{W(t)\\ge m\\}$\n\nif $W(t)\\ge m$, then we are guaranteed that $\\tau_m\\le t$. \n\n$\\mathbb{P}\\{\\tau_m\\le t,W(t)\\ge m\\}=\\mathbb{P}\\{W(t)\\ge m\\}$\n\nso,$\\mathbb{P}\\{\\tau_m\\le t\\}=2\\mathbb{P}\\{W(t)\\ge m\\}=\\frac{2}{\\sqrt{2\\pi t}}\\int_{m}^\\infty e^{-\\frac{x^2}{2t}}dx=\\frac{2}{\\sqrt{2\\pi}}\\int_{\\frac{\\vert m\\vert}{\\sqrt{t}}}^\\infty e^{-\\frac{y^2}{2}}dy$\n\n### Distribution of Brownian Motion and Its Maximum\n\ndefine the **maximum to date** for Brownian motion\n\n$M(t)=\\max_{0\\le s\\le t}W(s)$\n\nUse the reflection equality, we can obtain the joint distribution of $W(t)$\n and $M(t)$\n\n**Theorem** For $t>0$, the joint density of $(M(t),W(t))$ is\n\n$f_{M(t),W(t)}(m,w)=\\frac{2(2m-w)}{t\\sqrt{2\\pi t}}e^{-\\frac{(2m-w)^2}{2t}}$\n\nPROOF\n\n$\\mathbb{P}\\{M(t)\\ge m,W(t)\\le w\\}=\\int_m^\\infty\\int_{-\\infty}^wf_{M(t),W(t)}(x,y)dydx$\n\n$\\mathbb{P}\\{W(t)\\ge 2m-w\\}=\\frac{1}{\\sqrt{2\\pi t}}\\int_{2m-w}^\\infty e^{-\\frac{z^2}{2t}}dz$\n\nFrom the reflection equality, \n\n$\\frac{1}{\\sqrt{2\\pi t}}\\int_{2m-w}^\\infty e^{-\\frac{z^2}{2t}}dz= \\int_m^\\infty\\int_{-\\infty}^wf_{M(t),W(t)}(x,y)dydx$\n\nDifferentiate with respect to $m$\n\n$-\\int_{-\\infty}^wf_{M(t),W(t)}(m,y)dy=-\\frac{2}{\\sqrt{2\\pi t}}e^{-\\frac{(2m-w)^2}{2t}}$\n\nWith respect to $w$, then we obtain the distribution\n\n**Corollary** \n\nThe conditional distribution of $M(t)$ given $W(t)=w$ is $f_{M(t)\\vert W(t)}(m\\vert w)=\\frac{2(2m-w)}{t}e^{-\\frac{2m(m-w)}{t}}$","slug":"Stochastic Calculus","published":1,"updated":"2022-02-24T13:33:16.413Z","comments":1,"photos":[],"link":"","_id":"cl0110i7000019jpkhgg10eet","content":"<head>\n <script src=\"https://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML\" type=\"text/javascript\"></script>\n <script type=\"text/x-mathjax-config\">\n MathJax.Hub.Config({\n tex2jax: {\n skipTags: ['script', 'noscript', 'style', 'textarea', 'pre'],\n inlineMath: [['$','$']]\n }\n });\n </script>\n</head>\n\n\n<h1 id=\"General-Probability-Theory\"><a href=\"#General-Probability-Theory\" class=\"headerlink\" title=\"General Probability Theory\"></a>General Probability Theory</h1><h2 id=\"infinite-probability-spaces\"><a href=\"#infinite-probability-spaces\" class=\"headerlink\" title=\"infinite probability spaces\"></a>infinite probability spaces</h2><h3 id=\"sigma-代数\"><a href=\"#sigma-代数\" class=\"headerlink\" title=\"$\\sigma$-代数\"></a>$\\sigma$-代数</h3><p>$\\sigma-algebra$, F is a collection of subsets of $\\Omega$</p>\n<ol>\n<li>empty set belongs to it</li>\n<li>whenever a set belongs to it, its complement also belong to F</li>\n<li>the union of a sequence of sets in F belongs to F</li>\n</ol>\n<p>可以有推论:</p>\n<ol>\n<li>$\\Omega$ 一定在F中</li>\n<li>集合序列的交集也一定在F中</li>\n</ol>\n<h3 id=\"概率测量的定义-probability-measure\"><a href=\"#概率测量的定义-probability-measure\" class=\"headerlink\" title=\"概率测量的定义 probability measure\"></a>概率测量的定义 probability measure</h3><p>一个函数,定义域是F中的任意集合,值域是[0,1],满足:</p>\n<ol>\n<li><p>$P(\\Omega)=1$</p>\n</li>\n<li><p>$P(\\cup^\\infty_{n=1} A_n)=\\sum^\\infty_{n=1} P(A_n)$</p>\n<p> $triple(\\Omega,F,P)$称为概率空间</p>\n</li>\n</ol>\n<p>uniform(Lebesgue)measure on [0,1]:在0,1之间选取一个数,定义:</p>\n<p>$P(a,b)=P[a,b]=b-a,0\\le a \\le b\\le 1$</p>\n<p>可以用上述方式表述概率的集合的集合构成了sigma代数,从包含的所有闭区间出发,称为Borel sigma代数</p>\n<p>$(a,b)=\\cup_{n=1}^\\infty[a+\\frac{1}{n},b-\\frac{1}{n}]$ ,所以sigma代数中包含了所有开区间,分别取补集可以导出包含开区间与闭区间的并,从而导出所有集合 </p>\n<p>通过从闭区间出发,添加所有必要元素构成的sigma代数称之为$Borel \\quad\\sigma-algebra$ of subsets of [0,1] and is denoted B[0,1]</p>\n<p>event A occurs almost surely if P(A)=1</p>\n<h2 id=\"Random-variables-and-distributions\"><a href=\"#Random-variables-and-distributions\" class=\"headerlink\" title=\"Random variables and distributions\"></a>Random variables and distributions</h2><p>definition: a random variable is a real-valued function X defined on $\\Omega$ with the property that for every Borel subset B of <strong>R,</strong> the subset of $\\Omega$ given by:</p>\n<p>$$<br>\\begin{equation*}{x\\in B}={\\omega \\in \\Omega ; X(\\omega )\\in B}\\end{equation*}<br>$$</p>\n<p>is in the $\\sigma$-algebra F</p>\n<p>本质是把事件映射为实数,同时为了保证可以拟映射,要求函数可测。</p>\n<p>构造R的Borel子集?从所有的闭区间出发,闭区间的交——特别地,开区间也包含进来,从而开集包含进来 ,因为每个开集可以写成开区间序列的并。闭集也是Borel集合,因为是开集的补集。</p>\n<p>关注X取值包含于某集合而不是具体的值</p>\n<p>Definition: let X be a random variable on a probability space, the distribution measure of X is the probability measure $\\mu _X$that assigns to each Borel subset B of R the mass $\\mu _X(B)=P{X\\in B}$ </p>\n<p>Random variable 有distribution 但两者不等同,两个不同的Random variable 可以有相同的distribution,一个单独的random variable 可以有两个不同的distribution</p>\n<p>cdf:$F(x)=P{X\\le x}$</p>\n<p>$\\mu_X(x,y]=F(y)-F(x)$</p>\n<h2 id=\"Expectations\"><a href=\"#Expectations\" class=\"headerlink\" title=\"Expectations\"></a>Expectations</h2><p>$E(X)=\\sum X(\\omega )P(\\omega )$</p>\n<p>${\\Omega , F, P}$ random variable $X(\\omega )$ P是概率空间中的测度</p>\n<p>$A_k={\\omega \\in \\Omega ; y_k\\le X(\\omega ) < y_{k+1}}$</p>\n<p>lower Lebesgue sum $LS^-_{\\Pi}=\\sum y_k P(A_k)$</p>\n<p>the maximal distance between the $y_k$ partition points approaches zero, we get Lebesgue integral$\\int_{\\Omega}X(\\omega )dP(\\omega)$</p>\n<p>Lebesgue integral相当于把积分概念拓展到可测空间,而不是单纯的更换了求和方式。横坐标实际上是$\\Omega$的测度。</p>\n<p>if the random variables X can take both positive and negative values, we can define the positive and negative parts of X:</p>\n<p>$X^+=max{X,0}$, $X^-=min{-X,0}$</p>\n<p>$\\int XdP=\\int X^+dP-\\int X^- dP$</p>\n<p><strong>Comparison</strong></p>\n<p>If $X\\le Y$ almost surely, and if the Lebesgue integral are defined, then</p>\n<p>$\\int _{\\Omega}X(\\omega)dP(\\omega)\\le \\int _{\\Omega}Y(\\omega)dP(\\omega)$</p>\n<p>If $X=Y$ almost surely, and if the Lebesgue integral are defined, then</p>\n<p>$\\int _{\\Omega}X(\\omega)dP(\\omega)=\\int _{\\Omega}Y(\\omega)dP(\\omega)$</p>\n<p><strong>Integrability, Linearity …</strong></p>\n<p><strong>Jensen’s inequality</strong></p>\n<p>if $\\phi$ is a convex, real-valued function defined on R and if $E|X|<\\infty$ ,then</p>\n<p>$\\phi(EX)\\le E\\phi(X)$</p>\n<p>$\\mathcal{B} (\\mathbb{R})$ be the sigma-algebra of Borel subsets of $\\mathbb{R}$, the Lebesgue measure $\\mathcal{L}$ on R assigns to each set $B\\in \\mathcal{B}(\\mathbb{R})$ a number in $[0,\\infty)$ or the value $\\infty$ so that:</p>\n<ol>\n<li>$\\mathcal{L}[a,b] =b-a$ </li>\n<li>if $B_1,B_2,B_3 \\dots$ is a sequence of disjoint sets in $\\mathcal{B}$ ,then we have the countable additivity property: $\\mathcal{L} (\\cup_{n=1}^\\infty B_n)=\\sum_{n=1}^\\infty \\mathcal{L} (B_n)$</li>\n</ol>\n<p>黎曼积分有且只有在区间中非连续点的集合的Lebesgue测度为零时有定义,即f在区间上几乎处处连续</p>\n<p>若f的Riemann积分在区间上存在,则f是Borel可测的,而且Riemann积分和Lebesgue积分一致。</p>\n<h3 id=\"convergence-of-integrals\"><a href=\"#convergence-of-integrals\" class=\"headerlink\" title=\"convergence of integrals\"></a>convergence of integrals</h3><p><strong>definition</strong></p>\n<p>$X_1,X_2,X_3\\dots$ be a sequence of random variables on the same probability space$(\\Omega, \\mathcal{F},\\mathbb{P})$, $X$ be another random variable. $X_1,X_2,X_3\\dots$ converges to $X$ almost surely $lim_{n\\to \\infty}X_n=X$ almost surely. if the set of $\\omega \\in \\Omega$ for the sequence has limit $X(\\omega)$ is a set with probability one. </p>\n<p>Strong law of Large Numbers: </p>\n<p>实的Borel可测的函数列$f_1,f_2,f_3\\dots$ defined on$\\mathbb{R}$, $f$ 也是实的Borel可测函数,the sequence converges to f almost every-where if 序列极限不为f的点的集合的 Lebesgue measure为零</p>\n<p>$lim_{n\\to \\infty}f_n=f \\textit{ almost everywhere}$</p>\n<p>当随机变量几乎趋于一致,他们的期望值趋于极限的期望。类似地,当函数几乎处处converge,通常情况下,他们的lebesgue积分收敛到极限的积分。特殊的情况,就是</p>\n<p>$lim_{n\\to \\infty}\\int f_n(x)dx\\ne \\int lim_{n\\to \\infty} f_n(x)dx$</p>\n<p>例如f是正态分布,左边为1,右边lebesgue积分为0</p>\n<p><strong>theorem</strong> <em>Monotone convergence</em> $X_1,X_2,X_3\\dots$ be a sequence of random variables converging almost surely to another random variable $X$ if 序列几乎单调不减,期望的极限是EX</p>\n<p>$lim_{n \\to \\infty}\\mathbb{E}X_n=\\mathbb{E} X$</p>\n<p>把这里的随机变量换成Borel可测实值函数,也是成立的</p>\n<p>$lim_{n\\to \\infty}\\int_{-\\infty}^{\\infty}f_n(x)dx=\\int_{-\\infty}^{\\infty}f(x)dx$</p>\n<p>即使随机变量几乎不发散,但期望可能发散</p>\n<p><strong>theorem Dominated convergence</strong> 如果随机变量序列几乎趋于一致于$X$,且满足 $|X_n|\\le Y$ almost surely for every n, $\\mathbb{E}Y<\\infty$, then $lim_{n\\to \\infty}EX_n=EX$</p>\n<p>对于Borel可测实值函数也一样成立:若$f_n(x)\\le g$ almost surely for every n, and $\\int_{-\\infty}^\\infty g(x)dx<\\infty$</p>\n<p>若$f_n(x)\\le g$ almost surely for every n, and $\\int_{-\\infty}^\\infty g(x)dx<\\infty$</p>\n<p>$lim_{n\\to \\infty}\\int_{-\\infty}^\\infty f_n(x)dx=\\int_{-\\infty}^\\infty f(x)dx$</p>\n<h2 id=\"Computation-of-Expectations\"><a href=\"#Computation-of-Expectations\" class=\"headerlink\" title=\"Computation of Expectations\"></a>Computation of Expectations</h2><p><strong>theorem</strong> $g$ is a Borel measurable function on $\\mathbb{R}$ Then:</p>\n<p>$\\mathbb{E} |g(X)|=\\int_\\mathbb{R} |g(x)|d\\mu_X(x)$ , if this quantity is finite, then$\\mathbb{E} g(X)=\\int_\\mathbb{R} g(x)d\\mu_X(x)$</p>\n<p>PROOF</p>\n<ol>\n<li><p>$\\mathbb{EI}_B(X)=\\mathbb{P}{X\\in B}=\\mu_X(B)=\\int_\\mathbb{R}\\mathbb{I}_B(x)d\\mu_X(x)$</p>\n</li>\n<li><p>nonnegative simple functions. A simple function is a finite sum of indicator functions times constants </p>\n<p> $$g(x)=\\sum\\alpha_k \\mathbb{I}_{B_k}(x)$$</p>\n<p> so </p>\n<p> $$\\mathbb{E}g(X)=\\mathbb{E}\\sum \\alpha_k \\mathbb{I}_{B_k}(X)=\\sum \\alpha_k\\int_R\\mathbb{I}_{B_k}d\\mu_X(x)=\\int_R(\\sum \\alpha_k\\mathbb{I}_{B_k}(x))d\\mu_X(x)=\\int_R g(x)d\\mu_X(x)$$</p>\n</li>\n<li><p>when g is nonnegative Borel-measurable functions. </p>\n<p> $$B_{k,n}={x;\\frac{k}{2^n}\\le g(x)\\le \\frac{k+1}{2^n}},k=0,1,2,\\dots,4^n-1$$</p>\n<p> $$g_n(x)=\\sum \\frac{k}{2^n}\\mathbb{I}_{B_{k,n}}(x)$$</p>\n<p> $$\\mathbb{E}g(X)=\\lim \\mathbb{E}g_n(X)=\\lim \\int_R g_n(x)d\\mu_X(x)=\\int_R g(x)d\\mu_X(x)$$</p>\n</li>\n<li><p>when g is general Borel-measurable function.</p>\n<p> $g^+(x)=\\max{g(x),0},g^-(x)\\min{-g(x),0}$</p>\n</li>\n</ol>\n<p><strong>Theorem</strong> $X$ is a random variable on a probability space $(\\Omega,\\mathcal{F},\\mathbb{P})$, and let g be a Borel measurable function on $\\mathbb{R}$. $X$ has a density $f$ </p>\n<p>$\\mathbb{E}|g(X)|=\\int|g(x)|f(x)dx$</p>\n<p>if quantity is finite, then </p>\n<p>$\\mathbb{E}g(X)=\\int g(x)f(x)dx$</p>\n<p>PROOF</p>\n<p>simple functions</p>\n<p>$$\\mathbb{E}g(X)=\\mathbb{E}(\\sum \\alpha_k \\mathbb{I}_{B_k}(X))=\\sum \\alpha_k \\mathbb{E}\\mathbb{I}_{B_k}(X)=\\sum \\alpha_k \\int \\mathbb{I}_{B_k}f(x)dx\\\\=\\int \\sum \\alpha<br>_k\\mathbb{I}_{B_k}(x)f(x)dx=\\int g(x)f(x)dx$$</p>\n<p>nonnegative Borel measurable functions</p>\n<p>$$\\mathbb{E}g_n(X)=\\int g_n(x)f(x)dx$$</p>\n<h2 id=\"Change-of-Measure\"><a href=\"#Change-of-Measure\" class=\"headerlink\" title=\"Change of Measure\"></a>Change of Measure</h2><p>We can use a positive random variable $Z$ to change probability measures on a space $\\Omega$. We need to do this when we change from the actual probability measure $\\mathbb{P}$ to the risk-neutral probability measure $\\widetilde{\\mathbb{P}}$ in models of financial markets.</p>\n<p>$$Z(\\omega)\\mathbb{P}(\\omega)=\\widetilde{\\mathbb{P}}(\\omega)$$</p>\n<p>to change from $\\mathbb{P}$ to $\\widetilde{\\mathbb{P}}$, we need to reassign probabilities in $\\Omega$ using $Z$ to tell us where in $\\Omega$ we should revise the probability upward and where downward. </p>\n<p><em>we should do this set-by-set, but not $\\omega$-by-$\\omega$. According to following theorem</em></p>\n<p><strong>Theorem</strong> let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space and let $Z$ be an almost surely nonnegative random variable with $\\mathbb{E}Z=1$. for $A\\in\\mathcal{F}$, define $\\widetilde{\\mathbb{P}}(A)=\\int_AZ(\\omega)d\\mathbb{P}(\\omega)$. Then $\\widetilde{\\mathbb{P}}$ is a probability measure. If $X$ is a nonnegative random variable, then$\\widetilde{\\mathbb{E}}X=\\mathbb{E}[XZ]$. If $Z$ is almost surely strictly positive, we also have $\\mathbb{E}Y=\\widetilde{\\mathbb{E}}[\\frac{Y}{Z}]$ for every nonnegative random variable $Y$.</p>\n<p>PROOF</p>\n<p>$\\widetilde{\\mathbb{P}}(\\Omega)=1$, and countably additive. </p>\n<p>countably additive</p>\n<p>let $A_1,A_2,A_3,\\dots$ be a sequence of disjoint sets in $\\mathcal{F}$, and define $B_n=\\cup_{k=1}^n A_k$</p>\n<p>we can use the monotone convergence theorem, to write</p>\n<p>$$\\widetilde{\\mathbb{P}}(\\cup _{k=1}^\\infty A_k)=\\widetilde{\\mathbb{P}}(B_\\infty)=\\int_\\Omega \\mathbb{I}_{B_\\infty}(\\omega)Z(\\omega)d\\mathbb{P}(\\omega)\\\\=\\lim_{n\\to \\infty}\\int_\\Omega \\mathbb{I}_{B_n}(\\omega)Z(\\omega)d\\mathbb{P}(\\omega)\\\\=\\lim_{n\\to \\infty}\\sum\\int_\\Omega\\mathbb{I}_{A_k}(\\omega)Z(\\omega)d\\mathbb{P}(\\omega)=\\sum_{k=1}^\\infty\\widetilde{\\mathbb{P}}(A_k)$$</p>\n<p><strong>Definition</strong> 如果两个概率测度下sigma代数中零概率的集合相同,那么称两个概率测度为equivalent</p>\n<p>在金融中,实际概率测度和风险中性概率测度就是equivalent的,在risk neutral world中almost work的hedge在actual world中一定也almost surely work</p>\n<p><strong>Definition</strong> 对于equivalent的两个概率测度以及它们之间的almost surely positive random variable, 这个随机变量$Z$称之为Radon-Nikodym derivative of$\\widetilde{\\mathbb{P}}$ with respect to $\\mathbb{P}$ and we write $Z=\\frac{d\\widetilde{\\mathbb{P}}}{d\\mathbb{P}}$, $Z$ 的存在性成为Radon-Nikodym Theorem</p>\n<h1 id=\"Information-and-Conditioning\"><a href=\"#Information-and-Conditioning\" class=\"headerlink\" title=\"Information and Conditioning\"></a>Information and Conditioning</h1><h2 id=\"Information-and-sigma-algebras\"><a href=\"#Information-and-sigma-algebras\" class=\"headerlink\" title=\"Information and $\\sigma$-algebras\"></a>Information and $\\sigma$-algebras</h2><p>The hedge must specify what position we will take in the underlying security at each future time contingent on how the uncertainty between the present time and that future time is resolved.</p>\n<p><strong>resolve sets by information</strong></p>\n<p>$\\Omega$ is the set of 8 possible outcomes of 3 coin tosses,</p>\n<p>$A_H={HHH,HHT,HTH,HTT},A_T={THH,THT,TTH,TTT}$</p>\n<p>if we are told the first coin toss only. the four sets that are resolved by the first coin toss form the $\\sigma$-algebra</p>\n<p>$\\mathcal{F}_1={\\phi,\\Omega,A_H,A_T}$</p>\n<p>this $\\sigma$-algebra contains the information learned by observing the first coin toss.</p>\n<p>如果某几个集合是resolved,那么他们的并,以及各自的补也是resolved,符合$\\sigma$-algebra</p>\n<p><strong>Definition</strong> let $\\Omega$ be a nonempty set. Let $T$ be a fixed positive number and assume that for each $t\\in [0,T]$ there is a $\\sigma-algebra$ $\\mathcal{F}(t)$. Assume further that if $s\\le t$, then every set in $\\mathcal{F}(s)$ is also in $\\mathcal{F}(t)$. Then we call the collection of $\\sigma-algebra$ $\\mathcal{F}(t)$ a filtration.</p>\n<p>At time $t$ we can know whether the true $\\omega$ lies in a set in $\\mathcal{F}(t)$</p>\n<p>Let $\\Omega=C_0[0,T]$, and assign probability to the sets in $\\mathcal{F}=\\mathcal{F}(T)$, then the paths $\\omega\\in C_0[0,T]$ will be the paths of the <strong>Brownian motion</strong>.</p>\n<p><strong>Definition</strong> Let $X$ be a random variable defined on a nonempty sample space $\\Omega$. The $\\sigma-algebra$ generated by $X$, denoted $\\sigma(X)$, is the collection of all subsets of $\\Omega$ of the form ${X\\in B}$, $B$<br> <strong>ranges over</strong> the Borel subsets of $\\mathbb{R}$</p>\n<p>这里的区别和简并有点像,随机变量是本征值,Filtration是量子态</p>\n<p><strong>Definition</strong> Let $X$ be a random variable defined on a nonempty sample space $\\Omega$. Let $\\mathcal{G}$ be a $\\sigma-algebra$ of subsets of $\\Omega$. If every set in $\\sigma(X)$ is also in $\\mathcal{G}$, we say that $X$ is $\\mathcal{G}-measurable$</p>\n<p>意味着$\\mathcal{G}$ 中的信息足够决定$X$ 的值。对于borel可测函数$f$,$f(X)$也是$\\mathcal{G}-measurable$的。对于多元函数同样成立</p>\n<p><strong>Definition</strong> Let $\\Omega$ be a nonempty sample space equipped with a filtration $\\mathcal{F}(t)$. Let </p>\n<p>$X(t)$ be a collection of random variables indexed by $t\\in [0,T]$, We say this collection of random variables is an adapted stochastic process if, for each $t$, the random variable $X(t)$ is $\\mathcal{F}(t)-measurable$ </p>\n<h2 id=\"Independence\"><a href=\"#Independence\" class=\"headerlink\" title=\"Independence\"></a>Independence</h2><p>对于一个随机变量和一个$\\sigma-algebra$ $\\mathcal{G}$, measurable 和 independent 是两种极端,但大部分情况下,$\\mathcal{G}$中但信息可以估计$X$, 但不足以确定$X$的值。</p>\n<p>Independence会受到概率度量的影响,但measurability不会。</p>\n<p>probability space $(\\Omega,\\mathcal{F},\\mathbb{P})$,$\\mathcal{G}\\in \\mathcal{F}, \\mathcal{H}\\in \\mathcal{F}$, $\\Omega$ 中的两个$\\sigma-algebra$$A$和$B$独立如果$\\mathbb{P}(A\\cap B)=\\mathbb{P}(A)\\cdot\\mathbb{P}(B)$, for all $A\\in \\mathcal{G},B\\in \\mathcal{H}$</p>\n<p>独立的定义可以拓展到随机变量($\\sigma-algebra$ they generate are independent)之间,随机变量与$\\sigma-algebra$之间。</p>\n<p><strong>Definition</strong> $(\\Omega,\\mathcal{F},\\mathbb{P})$ is a probability space and let $\\mathcal{G}_1,\\mathcal{G}_2,\\mathcal{G}_3\\dots$ be a sequence of $sub-\\sigma-algebra$ of $\\mathcal{F}$. For a fixed positive integer n, we say that the n $\\sigma-algebra$s $\\mathcal{G}_1,\\mathcal{G}_2,\\mathcal{G}_3\\dots\\mathcal{G}_n$ are independent if$\\mathbb{P}(A_1\\cap A_2\\cap \\dots\\cap A_n)=\\mathbb{P}<br>(A_1)\\mathbb{P}<br>(A_2)\\dots \\mathbb{P}<br>(A_n)$ for all $A_i\\in \\mathcal{G}_i$</p>\n<p>这个同样也可以拓展到随机变量之间以及随机变量与$\\sigma-algebra$之间。</p>\n<p><strong>Theorem</strong> Let $X$ and $Y$ be independent random variables, and let $f$ and $g$ be Borel measurable functions on $\\mathbb{R}$. Then$f(X)$ and $g(Y)$ are independent random variables.</p>\n<p>PROOF</p>\n<p>Let $A$ be in the $\\sigma-algebra$ generated by $f(X)$. This $\\sigma-algebra$ is a $sub-\\sigma -algebra$ of $\\sigma(X)$. </p>\n<p>这很自然,every set in $A$ is of the form${\\omega \\in \\Omega;f(X(\\omega))\\in C}\\text{,where }C\\text{ is a Borel subset of }\\mathbb{R}$. 只需要定义$D={x\\in \\mathbb{R};f(x)\\in C}$. Then we know$A\\in \\sigma(X)$. Let $B$ be the $\\sigma-algebra$ gnenerated by $g(Y)$, then $B\\in \\sigma(Y)$. 由于$X,Y$独立,所以$A,B$独立。</p>\n<p><strong>Definition</strong> Let$X$ and $Y$ be random variables. The pair of random variables$(X,Y)$ takes values in the plane$\\mathbb{R}^2$, and the joint distribution measure of $(X,Y)$ is given by$\\mu_{X,Y}(C)=\\mathbb{P}{(X,Y)\\in C}$ for all Borel sets $C\\in \\mathbb{R}^2$</p>\n<p>同样满足概率度量的两个条件:全空间测度为1,以及countable additivity preperty</p>\n<p><strong>Theorem</strong> Let $X$ and $Y$ be random variables. The following conditions and equivalent.</p>\n<ol>\n<li><p>$X$ and $Y$ are independent</p>\n</li>\n<li><p>the joint distribution measure factors:</p>\n<p> $\\mu_{X,Y}(A\\times B)=\\mu_X(A)\\mu_Y(B)$ for all Borel subsets$A\\in \\mathbb{R},B\\in\\mathbb{R}$</p>\n</li>\n<li><p>the joint cumulative distribution function factors</p>\n<p> $F_{X,Y}(a,b)=F_X(a)F_Y(b)$ for all $a\\in \\mathbb{R},b\\in \\mathbb{R}$</p>\n</li>\n<li><p>the joint moment-generating function factor:(矩母函数)</p>\n<p> $\\mathbb{E}e^{uX+vY}=\\mathbb{E}e^{uX}\\cdot\\mathbb{E}e^{vY}$</p>\n</li>\n<li><p>the joint density factors(if there is one)</p>\n<p> $f_{X,Y}(x,y)=f_X(x)f_Y(y)$ for almost every$x\\in\\mathbb{R},y\\in\\mathbb{R}$</p>\n</li>\n</ol>\n<p>conditions above imply but are not equivalent to:</p>\n<ol>\n<li>$\\mathbb{E}[XY]=\\mathbb{E}X\\cdot\\mathbb{E}Y$ provided $\\mathbb{E}|XY|<\\infty$</li>\n</ol>\n<p><strong>Definition</strong> Let $X$ be a random variable whose expected value is defined. The variance of $X$, denoted $Var(X)$ is $Var(X)=\\mathbb{E}[(X-\\mathbb{E}X)^2]=\\mathbb{E}[X^2]-(\\mathbb{E}X)^2$</p>\n<p>covariance of $X$ and $Y$ is $Cov(X,Y)=\\mathbb{E}[(X-\\mathbb{E}X)(Y-\\mathbb{E}Y)]=\\mathbb{E}[XY]-\\mathbb{E}X\\cdot\\mathbb{E}Y$</p>\n<p>correlation coefficient of $X$and $Y$ is $\\rho(X,Y)=\\frac{Cov(X,Y)}{\\sqrt{Var(X)Var(Y)}}$</p>\n<p>if $\\rho(X,Y)=0$, we say that $X$ and $Y$ are uncorrelated</p>\n<h2 id=\"General-Conditional-Expectations\"><a href=\"#General-Conditional-Expectations\" class=\"headerlink\" title=\"General Conditional Expectations\"></a>General Conditional Expectations</h2><p><strong>Definition</strong> Let$(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space, let $\\mathcal{G}$ be a sub-$\\sigma$-algebra of $\\mathcal{F}$, and let $X$ be a random variable that is either nonnegative or integrable. The conditional expectation of $X$ given $\\mathcal{G}$, denoted$\\mathbb{E}[X|\\mathcal{G}]$, is any random variable that satisfies</p>\n<ol>\n<li><strong>Measurability $\\mathbb{E}[X|\\mathcal{G}]$</strong> is $\\mathcal{G}$ measurable</li>\n<li><strong>Partial averaging $\\int_A\\mathbb{E}[X|\\mathcal{G}(\\omega)]=\\int_AX(\\omega)d\\mathbb{P}(\\omega)$</strong> for all $A\\in \\mathcal{G}$</li>\n</ol>\n<p>If $\\mathcal{G}$ is generated by some other random variable $W$, then we can write$\\mathbb{E}[X|W]$</p>\n<p>(1) means although the estimate of $X$based on the information in $\\mathcal{G}$ is itself a random variable, the value of the estimate $\\mathbb{E}[X|\\mathcal{G}]$ can be determined from the information in $\\mathcal{G}$</p>\n<p>存在性可以由Radon-Nikodym Theorem证明</p>\n<p>唯一性的证明如下:If $Y$ and $Z$ both satisfy conditions, then their difference $Y-Z$ is as well, and thus the set $A={Y-Z>0}$ is in $\\mathcal{G}$. 根据(2),$\\int_AY(\\omega)d\\mathbb{P}(\\omega)=\\int_AX(\\omega)d\\mathbb{P}(\\omega)=\\int_AZ(\\omega)d\\mathbb{P}(\\omega)$</p>\n<p>Hence $Y=Z$ almost surely.</p>\n<p><strong>Theorem</strong> Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space and let $\\mathcal{G}$ be a sub-$\\sigma$-algebra of $\\mathcal{F}$</p>\n<ol>\n<li><p>linearity of conditional expectations<br>$\\mathbb{E}[c_1X+c_2Y|\\mathcal{G}]=c_1\\mathbb{E}[X|\\mathcal{G}]+c_2\\mathbb{E}[Y|\\mathcal{G}]$</p>\n</li>\n<li><p>taking out what is known. </p>\n<p> If $X$ is $\\mathcal{G}$-measurable</p>\n<p> $\\mathbb{E}[XY|\\mathcal{G}]=X\\mathbb{E}[Y|\\mathcal{G}]$</p>\n</li>\n<li><p>iterated conditioning.</p>\n<p> If $\\mathcal{H}$ is a sub-$\\sigma$-algebra of $\\mathcal{G}$ and $X$ is an integrable random variable, then</p>\n<p> $\\mathbb{E}[\\mathbb{E}[X|\\mathcal{G}]|\\mathcal{H}]=\\mathbb{E}[X|\\mathcal{H}]$</p>\n</li>\n<li><p>independence</p>\n<p> If $X$ is independent of $\\mathcal{G}$, then $\\mathbb{E}[X|\\mathcal{G}]=\\mathbb{E}X$</p>\n</li>\n<li><p>conditional Jensen’s inequality</p>\n<p> $\\mathbb{E}[\\phi(X)|\\mathcal{G}]\\ge\\phi(\\mathbb{E}[X|\\mathcal{G}])$</p>\n</li>\n</ol>\n<p><strong>Lemma</strong> Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space, and let $\\mathcal{G}$ be a sub-$\\sigma$-algebra of $\\mathcal{F}$. Suppose the random variables $X_1,\\dots,X_K$ are $\\mathcal{G}$-measurable and the random variables$Y_1,\\dots,Y_L$ are independent of $\\mathcal{G}$. Let $f(x_1,\\dots,x_K,y_1,\\dots,y_L)$ be a function of the dummy variables, and define: </p>\n<p>$g(x_1,\\dots,x_K)=\\mathbb{E}f(x1,\\dots,x_K,Y_1,\\dots,Y_L)$</p>\n<p>This means holding $X_i$ constant and integrate out $Y_i$.</p>\n<p>Then,$\\mathbb{E}[f(X_1,\\dots,X_K,Y_1,\\dots,Y_L)|\\mathcal{G}]=g(X_1,\\dots,X_K)$</p>\n<p><strong>Definition</strong> Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space, let $T$ be a fixed positive number, and let $\\mathcal{F}(t)$, $0\\le t\\le T$, be a filtration of $sub-\\sigma-algebra$ of $\\mathcal{F}$. Consider an adapted stochastic process $M(t)$:</p>\n<ol>\n<li>If $\\mathbb{E}[M(t)|\\mathcal{F}(s)]=M(s)$ for all $0\\le s\\le t \\le T$, this process is a <em><strong>martingale</strong></em>. It has no tendency to rise or fall.</li>\n<li>If $\\mathbb{E}[M(t)|\\mathcal{F}(s)]\\le M(s)$ for all $0\\le s\\le t \\le T$, this process is a <em><strong>supermartingale</strong></em>. It has no tendency to rise, it may have a tendency to fall.</li>\n<li>If $\\mathbb{E}[M(t)|\\mathcal{F}(s)]\\ge M(s)$ for all $0\\le s\\le t \\le T$, this process is a <em><strong>submartingale</strong></em>. It has no tendency to fall, it may have a tendency to rise.</li>\n</ol>\n<p><strong>Definition</strong> Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space, let $T$ be a fixed positive number, and let $\\mathcal{F}(t)$, $0\\le t\\le T$, be a filtration of $sub-\\sigma-algebra$ of $\\mathcal{F}$. Consider an adapted stochastic process $X(t)$. Assume that for all $0\\le s\\le t\\le T$ and for every nonnegative, Borel-measuable function $f$, there is another Borel-measuable function $g$ such that:</p>\n<p>$\\mathbb{E}[f(X(t))|\\mathcal{F}(s)]=g(X(s))$</p>\n<p>Then we say that the X is a Markov process</p>\n<h1 id=\"Brownian-Motion\"><a href=\"#Brownian-Motion\" class=\"headerlink\" title=\"Brownian Motion\"></a>Brownian Motion</h1><h2 id=\"Scaled-Random-Walks\"><a href=\"#Scaled-Random-Walks\" class=\"headerlink\" title=\"Scaled Random Walks\"></a>Scaled Random Walks</h2><h3 id=\"Symmetric-Random-Walk\"><a href=\"#Symmetric-Random-Walk\" class=\"headerlink\" title=\"Symmetric Random Walk\"></a>Symmetric Random Walk</h3><p>To build a <strong>symmetric random walk</strong> we repeatedly toss a fair coin.</p>\n<p>$X_j=\\begin{cases}1 \\text{ if }\\omega_j=H\\\\-1\\text{ if }\\omega_j=T\\end{cases}$</p>\n<p>$M_0=0$, $M_k=\\sum_{j=1}^kX_j$</p>\n<p>the process $M_k$ is a <em>symmetric random walk.</em></p>\n<h3 id=\"Increments-of-the-Symmetric-Random-Walk\"><a href=\"#Increments-of-the-Symmetric-Random-Walk\" class=\"headerlink\" title=\"Increments of the Symmetric Random Walk\"></a>Increments of the Symmetric Random Walk</h3><p>A random walk has independent increments(独立增量性)</p>\n<p>if we choose nonnegative integers$0=k_0<k_1<\\cdots<k_m$ , the random variables $M_{k_i}-M_{k_{i-1}}$ are independent.</p>\n<p>Each of these random variables $M_{k_i}-M_{k_{i-1}}=\\sum_{j=k_{i+1}}^{k_{i+1}}X_j$ is called an increment of the random walk. </p>\n<p>Each increment has expected value 0 and variance $k_{i+1}-k_i$ . The variance is obvious because $X_j$ are independent.</p>\n<h3 id=\"Martingale-Property-for-the-Symmetric-Random-Walk\"><a href=\"#Martingale-Property-for-the-Symmetric-Random-Walk\" class=\"headerlink\" title=\"Martingale Property for the Symmetric Random Walk\"></a>Martingale Property for the Symmetric Random Walk</h3><p>We choose nonnegative integers $k<l$ and compute:</p>\n<p>$\\mathbb{E}[M_l|\\mathcal{F}_k]=\\mathbb{E}[(M_l-M_k)+M_k|\\mathcal{F}_k]=\\mathbb{E}[M_l-M_k|\\mathcal{F}_k]+\\mathbb{E}[M_k|\\mathcal{F}_k]=M_k$</p>\n<h3 id=\"Quadratic-Variation-of-the-Symmetric-Random-Walk\"><a href=\"#Quadratic-Variation-of-the-Symmetric-Random-Walk\" class=\"headerlink\" title=\"Quadratic Variation of the Symmetric Random Walk\"></a>Quadratic Variation of the Symmetric Random Walk</h3><p>the quadratic variation up to time $k$ is defined to be $[M,M]_k=\\sum_{j=1}^k(M_j-M_{j-1})^2=k$</p>\n<p>This is computed path-by-path. taking all the one step increments $M_j-M_{j-1}$ along that path, squaring these increments, and then summing them.</p>\n<p>Note that $[M,M]_k$ is the same as $Var(M_k)$, but the computations of these two quantities are quite different. $Var$ is computed by taking an average over all paths, taking their probability into account. If the random walk is not symmetric, the probability distribution would affect $Var$. On the contrary, the probability up and down do not affect the quadratic variation computation.</p>\n<h3 id=\"Scaled-Symmetric-Random-Walk\"><a href=\"#Scaled-Symmetric-Random-Walk\" class=\"headerlink\" title=\"Scaled Symmetric Random Walk\"></a>Scaled Symmetric Random Walk</h3><p>We fix a positive integer $n$ and define the <strong>scaled symmetric random walk</strong> $W^{(n)}(t)=\\frac{1}{\\sqrt{n}}M_{nt}$. If $nt$ is not an integer, we define $W^{(n)}(t)$ by linear interpolation between its values at the nearest points $s$ and $u$ to the left and right of $t$ for which $ns$ and $nu$ are integers. </p>\n<p>A Brownian motion is a scaled symmetric random walk with $n\\to \\infty$</p>\n<p>$\\mathbb{E}(W^{(n)}(t)-W^{(n)}(s))=0,Var(W^{(n)}(t)-W^{(n)}(s))=t-s$</p>\n<p>Let $0\\le s\\le t$ be given, and decompose $W^{(n)}(t)$ as: $W^{(n)}(t)=(W^{(n)}(t)-W^{(n)}(s))+W^{(n)}(s)$ </p>\n<p>$(W^{(n)}(t)-W^{(n)}(s))$ is independent of $\\mathcal{F}(s)$, the $\\sigma-algebra$ of information available at time s, and $W^{(n)}(s)$ is $\\mathcal{F}(s)$ measurable. So $\\mathbb{E}[W^{(n)}(t)|\\mathcal{F}(s)]=W^{(n)}(s)$</p>\n<p>The <strong>quadratic variation</strong> of the scaled random walk: </p>\n<p>$[W^{(n)},W^{(n)}](t)=\\sum_{j=1}^{nt}[W^{(n)}(\\frac{j}{n})-W^{(n)}(\\frac{j-1}{n})]^2=\\sum_{j=1}^{nt}[W^{(n)}[\\frac{1}{\\sqrt{n}}X_j]^2=\\sum_{j=1}^{nt}\\frac{1}{n}=t$</p>\n<h3 id=\"Limiting-Distribution-of-the-Scaled-Random-Walk\"><a href=\"#Limiting-Distribution-of-the-Scaled-Random-Walk\" class=\"headerlink\" title=\"Limiting Distribution of the Scaled Random Walk\"></a>Limiting Distribution of the Scaled Random Walk</h3><p><strong>Theorem: Central limit</strong> Fix $t\\ge 0$. As $n\\to \\infty$, the distribution of the scaled random walk $W^{(n)}(t)$ evaluated at time $t$ converges to the normal distribution with mean zero and variance $t$.</p>\n<p>PROOF</p>\n<p>For the normal density $f(s)=\\frac{1}{\\sqrt{2\\pi t}}e^{-\\frac{x^2}{2t}}$, the moment-generating function is </p>\n<p>$\\phi(u)=\\frac{1}{\\sqrt{2\\pi t}}\\int_{-\\infty}^\\infty \\exp{ux-\\frac{x^2}{2t}}dx=e^{\\frac{1}{2}u^2t}$</p>\n<p>If $t$ is such that $nt$ is an integer, then the moment-generating function for $W^{(n)}(t)$ is:</p>\n<p>$\\phi_n(u)=\\mathbb{E}e^{uW^{(n)}(t)}=\\mathbb{E}\\exp{\\frac{u}{\\sqrt{n}}M_{nt}}=\\mathbb{E}\\exp{\\frac{u}{\\sqrt{n}}\\sum_{j=1}^{nt}X_j}=\\mathbb{E}\\prod_{j=1}^{nt}\\exp{\\frac{u}{\\sqrt{n}}X_j}\\\\=\\prod_{j=1}^{nt}\\mathbb{E}\\exp{\\frac{u}{\\sqrt{n}}X_j}=\\prod_{j=1}^{nt}(\\frac{e^{\\frac{u}{\\sqrt{n}}}+e^{\\frac{-u}{\\sqrt{n}}}}{2})=(\\frac{e^{\\frac{u}{\\sqrt{n}}}+e^{\\frac{-u}{\\sqrt{n}}}}{2})^{nt}$</p>\n<p>when $n\\to \\infty$ , $\\phi(u)=e^{\\frac{1}{2}u^2t}$</p>\n<h3 id=\"Log-Normal-Distribution-as-the-Limit-of-the-Binomial-Model\"><a href=\"#Log-Normal-Distribution-as-the-Limit-of-the-Binomial-Model\" class=\"headerlink\" title=\"Log-Normal Distribution as the Limit of the Binomial Model\"></a>Log-Normal Distribution as the Limit of the Binomial Model</h3><p>We build a model for a stock price on the time interval from $0$ to $t$ by choosing an integer $n$ and constructing a binomial model for the stock price that takes $n$ steps per unit time. Up factor $u_n=1+\\frac{\\sigma}{\\sqrt{n}}$, down factor $u_d=1-\\frac{\\sigma}{\\sqrt{n}}$. $r=0.$</p>\n<p>The risk-neutral probabilities are then:</p>\n<p>$\\tilde{p}=\\frac{1+r-d_n}{u_n-d_n}=\\frac{1}{2}$, $\\tilde{q}=\\frac{u_n-1-r}{u_n-d_n}=\\frac{\\sigma/\\sqrt{n}}{2\\sigma/\\sqrt{n}}=\\frac{1}{2}$</p>\n<p>Random walk $M_{nt}=H_{nt}-T_{nt}$, while $nt=H_{nt}+T_{nt}$</p>\n<p>the stock price at time $t$ is $S_n(t)=S(0)u_n^{H_{nt}}d_n^{T_{nt}}=S(0)(1+\\frac{\\sigma}{\\sqrt{n}})^{\\frac{1}{2}(nt+M_{nt})}(1+\\frac{\\sigma}{\\sqrt{n}})^{\\frac{1}{2}(nt+M_{nt})}(1-\\frac{\\sigma}{\\sqrt{n}})^{\\frac{1}{2}(nt-M_{nt})}$</p>\n<p>we need to identify the distribution of this random variable as $n\\to \\infty$</p>\n<p><strong>Theorem</strong> As $n\\to \\infty$ , the distribution of $S_n(t)$ converges to the distribution of</p>\n<p>$S(t)=S(0)\\exp{\\sigma W(t)-\\frac{1}{2}\\sigma^2t}$ </p>\n<p>$W(t)$ is a normal random variable with mean zero and variance $t$</p>\n<p>PROOF:</p>\n<p>$\\log S_n(t)\\\\=\\log S(0)+\\frac{1}{2}(nt+M_{nt})\\log (1+\\frac{\\sigma}{\\sqrt{n}})+\\frac{1}{2}(nt-M_{nt})\\log (1-\\frac{\\sigma}{\\sqrt{n}})\\\\=\\log S(0)+\\frac{1}{2}(nt+M_{nt})(\\frac{\\sigma}{\\sqrt{n}}-\\frac{\\sigma^2}{2n}+O(n^{-3/2}))+\\frac{1}{2}(nt-M_{nt})(\\frac{\\sigma}{-\\sqrt{n}}-\\frac{\\sigma^2}{2n}+O(n^{-3/2}))\\\\=\\log S(0)+nt(-\\frac{\\sigma^2}{2n}+O(n^{-3/2}))+M_{nt}(\\frac{\\sigma}{\\sqrt{n}}+O(n^{-3/2}))=\\log S(0)-\\frac{1}{2}\\sigma^2t+\\sigma W^{(n)}(t)$</p>\n<p>By the <strong>Central Limit Theorem,</strong> we know that $\\frac{1}{\\sqrt{n}}M_{nt}=W^{(n)}(t)\\to W(t), \\text{when }n\\to \\infty$</p>\n<h2 id=\"Brownian-Motion-1\"><a href=\"#Brownian-Motion-1\" class=\"headerlink\" title=\"Brownian Motion\"></a>Brownian Motion</h2><h3 id=\"Definition-of-Brownian-Motion\"><a href=\"#Definition-of-Brownian-Motion\" class=\"headerlink\" title=\"Definition of Brownian Motion\"></a>Definition of Brownian Motion</h3><p><strong>Definition</strong> Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space. For each $\\omega\\in\\Omega$, suppose there is a continuous function $W(t)$ of $t\\ge 0$ that satisfies $W(0)=0$ that depends on $\\omega$. Then $W(t),t\\ge 0$ is a Brownian motion if for all $t_i$ the increments $W(t_i)-W(t_{i-1})$ are independent and each of these increments is normally distributed with $\\mathbb{E}[W(t_{i+1})-W(t_i)]=0,Var[W(t_{i+1})-W(t_i)]=t_{i+1}-t_i$</p>\n<p>Difference between BM and a scaled random walk: the scaled random walk has a natural time step and is linear between these time steps, whereas the BM has no linear pieces.</p>\n<h3 id=\"Distribution-of-Brownian-Motion\"><a href=\"#Distribution-of-Brownian-Motion\" class=\"headerlink\" title=\"Distribution of Brownian Motion\"></a>Distribution of Brownian Motion</h3><p>For any two times, the covariance of $W(s)$ and $W(t)$ for $s\\le t$ is</p>\n<p>$\\mathbb{E}[W(s)W(t)]=\\mathbb{E}[W(s)(W(t)-W(s))+W^2(s)]=\\mathbb{E}[W(s)]\\mathbb{E}[(W(t)-W(s))]+\\mathbb{E}[W^2(s)]=s$</p>\n<p>We compute the moment-generating function of the random vector$(W(t_1),W(t_2),\\dots,W(t_m))$</p>\n<p>$\\phi=\\mathbb{E}\\exp{u_mW(t_m)+\\dots+u_1W(t_1)}=\\mathbb{E}\\exp{u_m(W(t_m)-W(t_{m-1}))+\\dots+(u_1+u_2+\\dots+u_m)W(t_1)}=\\mathbb{E}\\exp{u_m(W(t_m)-W(t_{m-1}))}\\cdots \\mathbb{E}\\exp{(u_1+u_2+\\cdots+u_m)W(t_1)}=\\exp{\\frac{1}{2}u_m^2(t_m-t_{m-1})}\\cdots\\exp{(u_1+u_2+\\cdots+u_m)^2t_1}$</p>\n<p>The distribution of the Brownian increments can be specified by specifying the joint density or the joint moment-generating function of the random variables</p>\n<p><strong>Theorem</strong> Let$(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space. For each $\\omega\\in\\Omega$, suppose there is a continuous function $W(t)$ of $t\\ge 0$ that satisfies $W(0)=0$ and that depends on $\\omega$. </p>\n<ol>\n<li><p>For all $0< t_0< t_1\\cdots <t_m$, the increments are independent and each of these increments is normally distributed with mean and variance given by$\\mathbb{E}[W(t_{i+1})-W(t_i)]=0,Var[W(t_{i+1})-W(t_i)]=t_{i+1}-t_i$</p>\n</li>\n<li><p>For all $0< t_0< t_1\\cdots <t_m$, the random variables $W(t_i)$ are jointly normally distributed with means equal to zero and covariance matrix</p>\n<p> $\\begin{pmatrix} t_{1} &t_1 \\cdots & t_{1} \\\\ t_1&t_2\\cdots &t_2\\\\ \\vdots & \\ddots & \\vdots \\\\ t_{1} &t_2 \\cdots & t_{m} \\end{pmatrix}$ </p>\n</li>\n<li><p>the random variables have the joint moment-generating function mentioned before</p>\n</li>\n</ol>\n<h3 id=\"Filtration-for-Brownian-Motion\"><a href=\"#Filtration-for-Brownian-Motion\" class=\"headerlink\" title=\"Filtration for Brownian Motion\"></a>Filtration for Brownian Motion</h3><p><strong>Definition</strong> Let$(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space on which is defined a Brownian motion $W(t),t\\ge 0$. A filtration for the Brownian motion is a collection of $\\sigma$-algebra $\\mathcal{F}(t),t\\ge 0$, satisfying:</p>\n<ol>\n<li><strong>Information accumulates</strong></li>\n<li><strong>Adaptivity: $W(t)$</strong> is <strong>$\\mathcal{F}(t)$</strong>-measurable</li>\n<li><strong>Independence of future increments</strong></li>\n</ol>\n<p>$\\Delta(t),t\\ge0$, be a stochastic process. $\\Delta(t)$ is adapted to the filtration $\\mathcal{F}(t)$ if for each $t\\ge 0$ the random variable $\\Delta(t)$ if $\\mathcal{F}(t)$-measurable.</p>\n<p>There are two possibilities for the filtration $\\mathcal{F}(t)$ for a Brownian motion. </p>\n<ol>\n<li>to let $\\mathcal{F}(t)$ contain only the info obtained by observing the BM itself up to time $t$. </li>\n<li>to include in $\\mathcal{F}(t)$ info obtained by observing the BM and one or more other processes. But if the info in $\\mathcal{F}(t)$ includes observations of processes other than the BM $W$, this additional info is not allowed to give clues about the future increments because of property iii</li>\n</ol>\n<h3 id=\"Martingale-Property-for-Brownian-Motion\"><a href=\"#Martingale-Property-for-Brownian-Motion\" class=\"headerlink\" title=\"Martingale Property for Brownian Motion\"></a>Martingale Property for Brownian Motion</h3><p><strong>Theorem</strong> Brownian motion is a martingale</p>\n<h2 id=\"Quadratic-Variation\"><a href=\"#Quadratic-Variation\" class=\"headerlink\" title=\"Quadratic Variation\"></a>Quadratic Variation</h2><p>For BM, there is no natural step size. If we are given $T>0$, we could simply choose a step size, say $\\frac{T}{n}$ for some large $n$, and compute the quadratic variation up to time $T$ with this step size:</p>\n<p>$\\sum_{j=0}^{n-1}[W(\\frac{(j+1)T}{n})-W(\\frac{jT}{n})]^2$</p>\n<p>The variation of paths of BM is not zero, which makes stochastic calculus different from ordinary calculus</p>\n<h3 id=\"First-Order-Variation\"><a href=\"#First-Order-Variation\" class=\"headerlink\" title=\"First-Order Variation\"></a>First-Order Variation</h3><p>$FV_T(f)=|f(t_1)-f(0)|+|f(t_2)-f(t_1)|+\\dots+|f(T)-f(t_2)|=\\int_0^{t_1}f’(t)dt+\\dots+\\int_{t_2}^Tf’(t)dt=\\int_0^T|f’(t)|dt$</p>\n<p>We first choose a partition $\\Pi={t_0,t_1,\\dots,t_n}$ of $[0,T]$, which is a set of times. These will serve to determine the step size. The maximum step size of the partition will be denoted $\\Vert\\Pi\\Vert=\\max_{j=0,\\dots,n-1}(t_{j+1}-t_j)$. We then define:</p>\n<p>$FV_T(f)=\\lim_{\\Vert\\Pi\\Vert\\to0}\\sum_{j=0}^{n-1}\\vert f(t_{j+1})-f(t_j)\\vert$</p>\n<p>用中值定理可以证明与积分相等</p>\n<h3 id=\"Quadratic-Variation-1\"><a href=\"#Quadratic-Variation-1\" class=\"headerlink\" title=\"Quadratic Variation\"></a>Quadratic Variation</h3><p><strong>Definition</strong> Let $f(t)$ be a function defined for $0\\le t\\le T$. The quadratic variation to $f$ up to time $T$ is </p>\n<p>$[f,f](T)=\\lim_{\\Vert\\Pi\\Vert\\to0}\\sum_{j=0}^{n-1}\\vert f(t_{j+1})-f(t_j)\\vert$</p>\n<p>if $f$ is derivative, then $<a href=\"T\">f,f</a>=0$</p>\n<p>if $\\int_0^T\\vert f’(t^*_j)\\vert ^2dt$ is infinite, then $[f,f](T)$ lead to a $0\\cdot\\infty$ situation, which can be anything between $0$ and $\\infty$</p>\n<p><strong>Theorem</strong> Let $W$ be a Brownian motion. Then $[W,W](T)=T$ for all $T\\ge 0$ almost surely.</p>\n<p>PROOF</p>\n<p>Define the <em>sample quadratic variation</em> corresponding to the partition of $[0,T]$, $\\Pi ={t_0,t_1,\\dots,t_n}$ to be</p>\n<p> $Q_\\Pi=\\sum_{j=0}^{n-1}(W(t_{j+1})-W(t_j))^2$</p>\n<p>We can show that $Q_\\Pi$ converges to $T$ as $\\Vert\\Pi\\Vert\\to0$</p>\n<p>$\\mathbb{E}[(W(t_{j+1})-W(t_j))^2]=Var[W(t_{j+1})-W(t_j)]=t_{j+1}-t_j$ implies:</p>\n<p>$\\mathbb{E}Q_\\Pi=\\sum\\mathbb{E}[(W(t_{j+1})-W(t_j))^2]=\\sum(t_{j+1}-t_j)=T$</p>\n<p>$Var[(W(t_{j+1})-W(t_j))^2]=\\mathbb{E}[(W(t_{j+1})-W(t_j))^4]-2(t_{j+1}-t_j)\\mathbb{E}[(W(t_{j+1})-W(t_j))^2]+(t_{j+1}-t_j)^2$</p>\n<p>$\\mathbb{E}[(W(t_{j+1})-W(t_j))^4]=3(t_{j+1}-t_j)^2$,$\\mathbb{E}[(W(t_{j+1})-W(t_j))^2]=t_{j+1}-t_j$</p>\n<p>PROOF</p>\n<p>By Ito’s formula, we have</p>\n<p>$𝑊^4(t)=4\\int^𝑡_0𝑊^3_s𝑑𝑊_s+6\\int^𝑡_0𝑊^2_sds$</p>\n<p>$M(t):=\\int_0^tW_s^3dW_s=0$ is a martingale and $\\mathbb{E}M(t)=\\mathbb{E}M(0)=0$</p>\n<p>$\\mathbb{E}W^4(t)=6\\int_0^t\\mathbb{E}[W_s^2]ds=6\\int_0^tsds=3t^2$</p>\n<p>so $Var[(W(t_{j+1}-W(t_j))^4]=2(t_{j+1}-t_j)^2$</p>\n<p>and $Var(Q_\\Pi)=\\sum 2(t_{j+1}-t_j)^2\\le2\\Vert\\Pi\\Vert T$</p>\n<p>In particular, $\\lim_{\\Vert\\Pi\\Vert\\to 0}Var(Q_\\Pi)=0,lim_{\\Vert\\Pi\\Vert\\to0}Q_\\Pi=\\mathbb{E}Q_\\Pi=T$</p>\n<p>$(W(t_{j+1})-W(t_j))^2\\approx t_{j+1}-t_j$$(W(t_{j+1})-W(t_j))^2=t_{j+1}-t_j$ when $t_{j+1}-t_j$ is very small</p>\n<p>$dW(t)dW(t)=dt$ is the informal write</p>\n<p>$dWdt=0,dtdt=0$</p>\n<h3 id=\"Volatility-of-Geometric-Brownian-Motion\"><a href=\"#Volatility-of-Geometric-Brownian-Motion\" class=\"headerlink\" title=\"Volatility of Geometric Brownian Motion\"></a>Volatility of Geometric Brownian Motion</h3><p>geometric Brownian motion: $S(t)=S(0)\\exp{\\sigma W(t)+(\\alpha-\\frac{1}{2}\\sigma^2)t}$</p>\n<p>realized volatility: the sum of the squares of the log returns</p>\n<p>for $T_1=t_0<t_1<\\cdots<tm=T_2$,</p>\n<p>$\\sum (\\log\\frac{S(t_{j+1})}{S(t_j)})^2=\\sigma^2\\sum(W(t_{j+1})-W(t_j))^2+(\\alpha-\\frac{1}{2}\\sigma^2)^2\\sum(t_{j+1}-t_j)^2+2\\sigma (\\alpha-\\frac{1}{2}\\sigma^2)\\sum(W(t_{j+1})-W(t_j))(t_{j+1}-t_j)$</p>\n<p>When the maximum step size $\\Vert\\Pi\\Vert=\\max_{j=0,1,\\dots,m-1}(t_{j+1}-t_j)$ is small, then the first term is approximately equal to its limit $\\sigma^2(T_2-T_1)$,hence, we have:</p>\n<p>$\\frac{1}{T_2-T_1}\\sum(\\log\\frac{S(t_{j+1})}{S(t_j)})^2\\approx\\sigma^2$</p>\n<h2 id=\"Markov-Property\"><a href=\"#Markov-Property\" class=\"headerlink\" title=\"Markov Property\"></a>Markov Property</h2><p><strong>Theorem</strong> Let$W(t),t\\ge0$, be a Brownian motion and let $\\mathcal{F}(t),t\\ge0$ Be a filtration for this Brownian motion. Then $W(t)$ is a Markov process</p>\n<p>PROOF</p>\n<p>We need to show: $\\mathbb{E}[f(W(t))\\vert \\mathcal{F}(s)]=g(W(s))$ $g$ Exists whenever given $0\\le s\\le t,f$</p>\n<p>$\\mathbb{E}[f(W(t))\\vert\\mathcal{F}(s)]=\\mathbb{E}[f((W(t)-W(s))+W(s))\\vert\\mathcal{F}(s)]$</p>\n<p>$W(t)-W(s)$ is normally distributed with mean zero and variance $t-s$</p>\n<p>Replace $W(s)$ with a dummy variable $x$<br>, define $g(x)=\\mathbb{E}f(W(t)-W(s)+x)$, then </p>\n<p>$g(x)=\\frac{1}{\\sqrt{2\\pi(t-s)}}\\int f(w+x)\\exp{-\\frac{w^2}{2(t-s)}}dw=\\frac{1}{\\sqrt{2\\pi\\tau}}\\int f(y)\\exp{-\\frac{(y-x)^2}{2\\tau}}dy$</p>\n<p>Define the <em>transition density $p(\\tau,x,y):=\\frac{1}{\\sqrt{2\\pi\\tau}}e^{-\\frac{(y-x)^2}{2\\tau}},\\tau=t-s$</em></p>\n<p>$g(x)=\\int f(y)p(\\tau,x,y)dy$ </p>\n<p>And $\\mathbb{E}[f(W(t))\\vert\\mathcal{F}(s)]=\\int f(y)p(\\tau,W(s),y)dy$</p>\n<p>Conditioned on the information in $\\mathcal{F}(s)$, the conditional density of $W(t)$ is $p(\\tau,W(s),y)$. This is a density in the variable $y$, normal with mean $W(s)$ and variance $\\tau$. The only information from $\\mathcal{F}(s)$ that is relevant is the value of $W(s)$</p>\n<h2 id=\"First-Passage-Time-Distribution\"><a href=\"#First-Passage-Time-Distribution\" class=\"headerlink\" title=\"First Passage Time Distribution\"></a>First Passage Time Distribution</h2><p>exponential martingale corresponding to $\\sigma$: $Z(t)=\\exp{\\sigma W(t)-\\frac{1}{2}\\sigma^2t}$</p>\n<p><strong>Theorem</strong> Exponential martingale Let $W(t),t\\ge 0$, be a Brownian motion with a filtration $\\mathcal{F}(t),t\\ge 0$, and let $\\sigma$ be a constant, thew process $Z(t)$ is a martingale</p>\n<p>PROOF</p>\n<p>$\\mathbb{E}[Z(t)\\vert\\mathcal{F}(s)]=\\mathbb{E}[\\exp{\\sigma W(t)-\\frac{1}{2}\\sigma^2t}\\vert \\mathcal{F}(s)]=\\mathbb{E}[\\exp{\\sigma (W(t)-W(s))}\\cdot\\exp{\\sigma W(s)-\\frac{1}{2}\\sigma^2t}\\vert \\mathcal{F}(s)]=\\exp{\\sigma W(s)-\\frac{1}{2}\\sigma^2t}\\cdot\\mathbb{E}[\\exp{\\sigma (W(t)-W(s))}]$</p>\n<p>$W(t)-W(s)$ is a normal distribution with mean zero and variance $\\sigma$ so $\\mathbb{E}[\\exp{\\sigma (W(t)-W(s))}]=\\frac{1}{2}\\sigma^2(t-s)$</p>\n<p>$\\mathbb{E}[Z(t)\\vert\\mathcal{F}(s)]=Z(s)$</p>\n<p>Let $m$ be a real number, and define the first passage time to level $m$: $\\tau_m=\\min{t\\ge 0;W(t)=m}$ if the BM never reaches the level $m$, we set $\\tau_m=\\infty$. A martingale that is stopped at a stopping time is still martingale and thus must have constant expectation. So:</p>\n<p>$1=Z(0)=\\mathbb{E}Z(t\\land\\tau_m)=\\mathbb{E}[\\exp{\\sigma W(t\\land\\tau_m)-\\frac{1}{2}\\sigma^2(t\\land\\tau_m)}]$ $t\\land\\tau_m$ means the minimum of $t$ and $\\tau_m$</p>\n<p>If $\\tau_m<\\infty$, the term $\\exp{-\\frac{1}{2}\\sigma^2(t\\land\\tau_m)}$ is equal to $\\exp{-\\frac{1}{2}\\sigma^2\\tau_m}$ for large enough $t$. $\\tau_m=\\infty$, the result converges to zero. So: </p>\n<p>$\\lim_{t\\to\\infty}\\exp{\\sigma W(t\\land\\tau_m)-\\frac{1}{2}\\sigma^2(t\\land\\tau_m)}=\\mathbb{I}_\\exp{\\sigma m-\\frac{1}{2}\\sigma^2\\tau_m\\}$</p>\n<p>now we can obtain:</p>\n<p>$1=\\mathbb{E}[\\mathbb{I}_\\exp{\\sigma m-\\frac{1}{2}\\sigma^2\\tau_m}]$</p>\n<p>$\\mathbb{E}[\\mathbb{I}_\\exp{-\\frac{1}{2}\\sigma^2\\tau_m}]=e^{-\\sigma m}$</p>\n<p>when $\\sigma\\to0$, we get $\\mathbb{P}{\\tau_m<\\infty}=1$</p>\n<p>$\\tau_m$ is finite almost surely, so we may drop the indicator to obtain:</p>\n<p>$\\mathbb{E}[\\exp{-\\frac{1}{2}\\sigma^2\\tau_m}]=e^{-\\sigma m}$</p>\n<p><strong>Theorem</strong> For $m\\in \\mathbb{R}$, the first passage time of Brownian motion to level $m$ is finite almost surely, and the Laplace transform of its distribution is given by </p>\n<p>$\\mathbb{E}e^{-\\alpha \\tau_m}=e^{-\\vert m \\vert\\sqrt{2\\alpha}}$ for all $\\alpha>0$</p>\n<p>differentiation: $\\mathbb{E}[\\tau_me^{-\\alpha\\tau_m}]=\\frac{\\vert m\\vert}{\\sqrt{2\\alpha}}e^{-\\vert m\\vert\\sqrt{2\\alpha}}$ for all $\\alpha>0$</p>\n<p>let $\\alpha\\to 0$ get obtain $\\mathbb{E}\\tau_m=\\infty$ so long as $m\\neq0$</p>\n<h2 id=\"Reflection-Principle\"><a href=\"#Reflection-Principle\" class=\"headerlink\" title=\"Reflection Principle\"></a>Reflection Principle</h2><h3 id=\"Reflection-Equality\"><a href=\"#Reflection-Equality\" class=\"headerlink\" title=\"Reflection Equality\"></a>Reflection Equality</h3><p>for each Brownian motion path that reaches level m prior to time t but is at a level w below m at time t, there is a “reflected path” that is at level $2m-w$ at time $t$. This reflected path is constructed by switching the up and down moves of the Brownian motion from time $\\tau_m$onward.</p>\n<p><strong>Reflection equality</strong></p>\n<p>$\\mathbb{P}{\\tau_m\\le t,W(t)\\le w}=\\mathbb{P}{W(t)\\ge 2m-w},w\\le m,m>0$</p>\n<h3 id=\"First-Passage-Time-Distribution-1\"><a href=\"#First-Passage-Time-Distribution-1\" class=\"headerlink\" title=\"First Passage Time Distribution\"></a>First Passage Time Distribution</h3><p><strong>Theorem</strong> For all $m\\neq0$, the random variable $\\tau_m$ has cumulative distribution function:</p>\n<p>$\\mathbb{P}{\\tau_m\\le t}=\\frac{2}{\\sqrt{2\\pi}}\\int_{\\frac{\\vert m\\vert}{\\sqrt{t}}}^\\infty e^{-\\frac{y^2}{2}}dy$</p>\n<p>$f_{\\tau_m}(t)=\\frac{d}{dt}\\mathbb{P}=\\frac{\\vert m\\vert}{t\\sqrt{2\\pi t}}e^{-\\frac{m^2}{2t}}$</p>\n<p>PROOF</p>\n<p>Use the reflection equality, we obtain</p>\n<p>$\\mathbb{P}{\\tau_m\\le t,W(t)\\le m}=\\mathbb{P}{W(t)\\ge m}$</p>\n<p>if $W(t)\\ge m$, then we are guaranteed that $\\tau_m\\le t$. </p>\n<p>$\\mathbb{P}{\\tau_m\\le t,W(t)\\ge m}=\\mathbb{P}{W(t)\\ge m}$</p>\n<p>so,$\\mathbb{P}{\\tau_m\\le t}=2\\mathbb{P}{W(t)\\ge m}=\\frac{2}{\\sqrt{2\\pi t}}\\int_{m}^\\infty e^{-\\frac{x^2}{2t}}dx=\\frac{2}{\\sqrt{2\\pi}}\\int_{\\frac{\\vert m\\vert}{\\sqrt{t}}}^\\infty e^{-\\frac{y^2}{2}}dy$</p>\n<h3 id=\"Distribution-of-Brownian-Motion-and-Its-Maximum\"><a href=\"#Distribution-of-Brownian-Motion-and-Its-Maximum\" class=\"headerlink\" title=\"Distribution of Brownian Motion and Its Maximum\"></a>Distribution of Brownian Motion and Its Maximum</h3><p>define the <strong>maximum to date</strong> for Brownian motion</p>\n<p>$M(t)=\\max_{0\\le s\\le t}W(s)$</p>\n<p>Use the reflection equality, we can obtain the joint distribution of $W(t)$<br> and $M(t)$</p>\n<p><strong>Theorem</strong> For $t>0$, the joint density of $(M(t),W(t))$ is</p>\n<p>$f_{M(t),W(t)}(m,w)=\\frac{2(2m-w)}{t\\sqrt{2\\pi t}}e^{-\\frac{(2m-w)^2}{2t}}$</p>\n<p>PROOF</p>\n<p>$\\mathbb{P}{M(t)\\ge m,W(t)\\le w}=\\int_m^\\infty\\int_{-\\infty}^wf_{M(t),W(t)}(x,y)dydx$</p>\n<p>$\\mathbb{P}{W(t)\\ge 2m-w}=\\frac{1}{\\sqrt{2\\pi t}}\\int_{2m-w}^\\infty e^{-\\frac{z^2}{2t}}dz$</p>\n<p>From the reflection equality, </p>\n<p>$\\frac{1}{\\sqrt{2\\pi t}}\\int_{2m-w}^\\infty e^{-\\frac{z^2}{2t}}dz= \\int_m^\\infty\\int_{-\\infty}^wf_{M(t),W(t)}(x,y)dydx$</p>\n<p>Differentiate with respect to $m$</p>\n<p>$-\\int_{-\\infty}^wf_{M(t),W(t)}(m,y)dy=-\\frac{2}{\\sqrt{2\\pi t}}e^{-\\frac{(2m-w)^2}{2t}}$</p>\n<p>With respect to $w$, then we obtain the distribution</p>\n<p><strong>Corollary</strong> </p>\n<p>The conditional distribution of $M(t)$ given $W(t)=w$ is $f_{M(t)\\vert W(t)}(m\\vert w)=\\frac{2(2m-w)}{t}e^{-\\frac{2m(m-w)}{t}}$</p>\n","site":{"data":{}},"excerpt":"","more":"<head>\n <script src=\"https://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML\" type=\"text/javascript\"></script>\n <script type=\"text/x-mathjax-config\">\n MathJax.Hub.Config({\n tex2jax: {\n skipTags: ['script', 'noscript', 'style', 'textarea', 'pre'],\n inlineMath: [['$','$']]\n }\n });\n </script>\n</head>\n\n\n<h1 id=\"General-Probability-Theory\"><a href=\"#General-Probability-Theory\" class=\"headerlink\" title=\"General Probability Theory\"></a>General Probability Theory</h1><h2 id=\"infinite-probability-spaces\"><a href=\"#infinite-probability-spaces\" class=\"headerlink\" title=\"infinite probability spaces\"></a>infinite probability spaces</h2><h3 id=\"sigma-代数\"><a href=\"#sigma-代数\" class=\"headerlink\" title=\"$\\sigma$-代数\"></a>$\\sigma$-代数</h3><p>$\\sigma-algebra$, F is a collection of subsets of $\\Omega$</p>\n<ol>\n<li>empty set belongs to it</li>\n<li>whenever a set belongs to it, its complement also belong to F</li>\n<li>the union of a sequence of sets in F belongs to F</li>\n</ol>\n<p>可以有推论:</p>\n<ol>\n<li>$\\Omega$ 一定在F中</li>\n<li>集合序列的交集也一定在F中</li>\n</ol>\n<h3 id=\"概率测量的定义-probability-measure\"><a href=\"#概率测量的定义-probability-measure\" class=\"headerlink\" title=\"概率测量的定义 probability measure\"></a>概率测量的定义 probability measure</h3><p>一个函数,定义域是F中的任意集合,值域是[0,1],满足:</p>\n<ol>\n<li><p>$P(\\Omega)=1$</p>\n</li>\n<li><p>$P(\\cup^\\infty_{n=1} A_n)=\\sum^\\infty_{n=1} P(A_n)$</p>\n<p> $triple(\\Omega,F,P)$称为概率空间</p>\n</li>\n</ol>\n<p>uniform(Lebesgue)measure on [0,1]:在0,1之间选取一个数,定义:</p>\n<p>$P(a,b)=P[a,b]=b-a,0\\le a \\le b\\le 1$</p>\n<p>可以用上述方式表述概率的集合的集合构成了sigma代数,从包含的所有闭区间出发,称为Borel sigma代数</p>\n<p>$(a,b)=\\cup_{n=1}^\\infty[a+\\frac{1}{n},b-\\frac{1}{n}]$ ,所以sigma代数中包含了所有开区间,分别取补集可以导出包含开区间与闭区间的并,从而导出所有集合 </p>\n<p>通过从闭区间出发,添加所有必要元素构成的sigma代数称之为$Borel \\quad\\sigma-algebra$ of subsets of [0,1] and is denoted B[0,1]</p>\n<p>event A occurs almost surely if P(A)=1</p>\n<h2 id=\"Random-variables-and-distributions\"><a href=\"#Random-variables-and-distributions\" class=\"headerlink\" title=\"Random variables and distributions\"></a>Random variables and distributions</h2><p>definition: a random variable is a real-valued function X defined on $\\Omega$ with the property that for every Borel subset B of <strong>R,</strong> the subset of $\\Omega$ given by:</p>\n<p>$$<br>\\begin{equation*}{x\\in B}={\\omega \\in \\Omega ; X(\\omega )\\in B}\\end{equation*}<br>$$</p>\n<p>is in the $\\sigma$-algebra F</p>\n<p>本质是把事件映射为实数,同时为了保证可以拟映射,要求函数可测。</p>\n<p>构造R的Borel子集?从所有的闭区间出发,闭区间的交——特别地,开区间也包含进来,从而开集包含进来 ,因为每个开集可以写成开区间序列的并。闭集也是Borel集合,因为是开集的补集。</p>\n<p>关注X取值包含于某集合而不是具体的值</p>\n<p>Definition: let X be a random variable on a probability space, the distribution measure of X is the probability measure $\\mu _X$that assigns to each Borel subset B of R the mass $\\mu _X(B)=P{X\\in B}$ </p>\n<p>Random variable 有distribution 但两者不等同,两个不同的Random variable 可以有相同的distribution,一个单独的random variable 可以有两个不同的distribution</p>\n<p>cdf:$F(x)=P{X\\le x}$</p>\n<p>$\\mu_X(x,y]=F(y)-F(x)$</p>\n<h2 id=\"Expectations\"><a href=\"#Expectations\" class=\"headerlink\" title=\"Expectations\"></a>Expectations</h2><p>$E(X)=\\sum X(\\omega )P(\\omega )$</p>\n<p>${\\Omega , F, P}$ random variable $X(\\omega )$ P是概率空间中的测度</p>\n<p>$A_k={\\omega \\in \\Omega ; y_k\\le X(\\omega ) < y_{k+1}}$</p>\n<p>lower Lebesgue sum $LS^-_{\\Pi}=\\sum y_k P(A_k)$</p>\n<p>the maximal distance between the $y_k$ partition points approaches zero, we get Lebesgue integral$\\int_{\\Omega}X(\\omega )dP(\\omega)$</p>\n<p>Lebesgue integral相当于把积分概念拓展到可测空间,而不是单纯的更换了求和方式。横坐标实际上是$\\Omega$的测度。</p>\n<p>if the random variables X can take both positive and negative values, we can define the positive and negative parts of X:</p>\n<p>$X^+=max{X,0}$, $X^-=min{-X,0}$</p>\n<p>$\\int XdP=\\int X^+dP-\\int X^- dP$</p>\n<p><strong>Comparison</strong></p>\n<p>If $X\\le Y$ almost surely, and if the Lebesgue integral are defined, then</p>\n<p>$\\int _{\\Omega}X(\\omega)dP(\\omega)\\le \\int _{\\Omega}Y(\\omega)dP(\\omega)$</p>\n<p>If $X=Y$ almost surely, and if the Lebesgue integral are defined, then</p>\n<p>$\\int _{\\Omega}X(\\omega)dP(\\omega)=\\int _{\\Omega}Y(\\omega)dP(\\omega)$</p>\n<p><strong>Integrability, Linearity …</strong></p>\n<p><strong>Jensen’s inequality</strong></p>\n<p>if $\\phi$ is a convex, real-valued function defined on R and if $E|X|<\\infty$ ,then</p>\n<p>$\\phi(EX)\\le E\\phi(X)$</p>\n<p>$\\mathcal{B} (\\mathbb{R})$ be the sigma-algebra of Borel subsets of $\\mathbb{R}$, the Lebesgue measure $\\mathcal{L}$ on R assigns to each set $B\\in \\mathcal{B}(\\mathbb{R})$ a number in $[0,\\infty)$ or the value $\\infty$ so that:</p>\n<ol>\n<li>$\\mathcal{L}[a,b] =b-a$ </li>\n<li>if $B_1,B_2,B_3 \\dots$ is a sequence of disjoint sets in $\\mathcal{B}$ ,then we have the countable additivity property: $\\mathcal{L} (\\cup_{n=1}^\\infty B_n)=\\sum_{n=1}^\\infty \\mathcal{L} (B_n)$</li>\n</ol>\n<p>黎曼积分有且只有在区间中非连续点的集合的Lebesgue测度为零时有定义,即f在区间上几乎处处连续</p>\n<p>若f的Riemann积分在区间上存在,则f是Borel可测的,而且Riemann积分和Lebesgue积分一致。</p>\n<h3 id=\"convergence-of-integrals\"><a href=\"#convergence-of-integrals\" class=\"headerlink\" title=\"convergence of integrals\"></a>convergence of integrals</h3><p><strong>definition</strong></p>\n<p>$X_1,X_2,X_3\\dots$ be a sequence of random variables on the same probability space$(\\Omega, \\mathcal{F},\\mathbb{P})$, $X$ be another random variable. $X_1,X_2,X_3\\dots$ converges to $X$ almost surely $lim_{n\\to \\infty}X_n=X$ almost surely. if the set of $\\omega \\in \\Omega$ for the sequence has limit $X(\\omega)$ is a set with probability one. </p>\n<p>Strong law of Large Numbers: </p>\n<p>实的Borel可测的函数列$f_1,f_2,f_3\\dots$ defined on$\\mathbb{R}$, $f$ 也是实的Borel可测函数,the sequence converges to f almost every-where if 序列极限不为f的点的集合的 Lebesgue measure为零</p>\n<p>$lim_{n\\to \\infty}f_n=f \\textit{ almost everywhere}$</p>\n<p>当随机变量几乎趋于一致,他们的期望值趋于极限的期望。类似地,当函数几乎处处converge,通常情况下,他们的lebesgue积分收敛到极限的积分。特殊的情况,就是</p>\n<p>$lim_{n\\to \\infty}\\int f_n(x)dx\\ne \\int lim_{n\\to \\infty} f_n(x)dx$</p>\n<p>例如f是正态分布,左边为1,右边lebesgue积分为0</p>\n<p><strong>theorem</strong> <em>Monotone convergence</em> $X_1,X_2,X_3\\dots$ be a sequence of random variables converging almost surely to another random variable $X$ if 序列几乎单调不减,期望的极限是EX</p>\n<p>$lim_{n \\to \\infty}\\mathbb{E}X_n=\\mathbb{E} X$</p>\n<p>把这里的随机变量换成Borel可测实值函数,也是成立的</p>\n<p>$lim_{n\\to \\infty}\\int_{-\\infty}^{\\infty}f_n(x)dx=\\int_{-\\infty}^{\\infty}f(x)dx$</p>\n<p>即使随机变量几乎不发散,但期望可能发散</p>\n<p><strong>theorem Dominated convergence</strong> 如果随机变量序列几乎趋于一致于$X$,且满足 $|X_n|\\le Y$ almost surely for every n, $\\mathbb{E}Y<\\infty$, then $lim_{n\\to \\infty}EX_n=EX$</p>\n<p>对于Borel可测实值函数也一样成立:若$f_n(x)\\le g$ almost surely for every n, and $\\int_{-\\infty}^\\infty g(x)dx<\\infty$</p>\n<p>若$f_n(x)\\le g$ almost surely for every n, and $\\int_{-\\infty}^\\infty g(x)dx<\\infty$</p>\n<p>$lim_{n\\to \\infty}\\int_{-\\infty}^\\infty f_n(x)dx=\\int_{-\\infty}^\\infty f(x)dx$</p>\n<h2 id=\"Computation-of-Expectations\"><a href=\"#Computation-of-Expectations\" class=\"headerlink\" title=\"Computation of Expectations\"></a>Computation of Expectations</h2><p><strong>theorem</strong> $g$ is a Borel measurable function on $\\mathbb{R}$ Then:</p>\n<p>$\\mathbb{E} |g(X)|=\\int_\\mathbb{R} |g(x)|d\\mu_X(x)$ , if this quantity is finite, then$\\mathbb{E} g(X)=\\int_\\mathbb{R} g(x)d\\mu_X(x)$</p>\n<p>PROOF</p>\n<ol>\n<li><p>$\\mathbb{EI}_B(X)=\\mathbb{P}{X\\in B}=\\mu_X(B)=\\int_\\mathbb{R}\\mathbb{I}_B(x)d\\mu_X(x)$</p>\n</li>\n<li><p>nonnegative simple functions. A simple function is a finite sum of indicator functions times constants </p>\n<p> $$g(x)=\\sum\\alpha_k \\mathbb{I}_{B_k}(x)$$</p>\n<p> so </p>\n<p> $$\\mathbb{E}g(X)=\\mathbb{E}\\sum \\alpha_k \\mathbb{I}_{B_k}(X)=\\sum \\alpha_k\\int_R\\mathbb{I}_{B_k}d\\mu_X(x)=\\int_R(\\sum \\alpha_k\\mathbb{I}_{B_k}(x))d\\mu_X(x)=\\int_R g(x)d\\mu_X(x)$$</p>\n</li>\n<li><p>when g is nonnegative Borel-measurable functions. </p>\n<p> $$B_{k,n}={x;\\frac{k}{2^n}\\le g(x)\\le \\frac{k+1}{2^n}},k=0,1,2,\\dots,4^n-1$$</p>\n<p> $$g_n(x)=\\sum \\frac{k}{2^n}\\mathbb{I}_{B_{k,n}}(x)$$</p>\n<p> $$\\mathbb{E}g(X)=\\lim \\mathbb{E}g_n(X)=\\lim \\int_R g_n(x)d\\mu_X(x)=\\int_R g(x)d\\mu_X(x)$$</p>\n</li>\n<li><p>when g is general Borel-measurable function.</p>\n<p> $g^+(x)=\\max{g(x),0},g^-(x)\\min{-g(x),0}$</p>\n</li>\n</ol>\n<p><strong>Theorem</strong> $X$ is a random variable on a probability space $(\\Omega,\\mathcal{F},\\mathbb{P})$, and let g be a Borel measurable function on $\\mathbb{R}$. $X$ has a density $f$ </p>\n<p>$\\mathbb{E}|g(X)|=\\int|g(x)|f(x)dx$</p>\n<p>if quantity is finite, then </p>\n<p>$\\mathbb{E}g(X)=\\int g(x)f(x)dx$</p>\n<p>PROOF</p>\n<p>simple functions</p>\n<p>$$\\mathbb{E}g(X)=\\mathbb{E}(\\sum \\alpha_k \\mathbb{I}_{B_k}(X))=\\sum \\alpha_k \\mathbb{E}\\mathbb{I}_{B_k}(X)=\\sum \\alpha_k \\int \\mathbb{I}_{B_k}f(x)dx\\\\=\\int \\sum \\alpha<br>_k\\mathbb{I}_{B_k}(x)f(x)dx=\\int g(x)f(x)dx$$</p>\n<p>nonnegative Borel measurable functions</p>\n<p>$$\\mathbb{E}g_n(X)=\\int g_n(x)f(x)dx$$</p>\n<h2 id=\"Change-of-Measure\"><a href=\"#Change-of-Measure\" class=\"headerlink\" title=\"Change of Measure\"></a>Change of Measure</h2><p>We can use a positive random variable $Z$ to change probability measures on a space $\\Omega$. We need to do this when we change from the actual probability measure $\\mathbb{P}$ to the risk-neutral probability measure $\\widetilde{\\mathbb{P}}$ in models of financial markets.</p>\n<p>$$Z(\\omega)\\mathbb{P}(\\omega)=\\widetilde{\\mathbb{P}}(\\omega)$$</p>\n<p>to change from $\\mathbb{P}$ to $\\widetilde{\\mathbb{P}}$, we need to reassign probabilities in $\\Omega$ using $Z$ to tell us where in $\\Omega$ we should revise the probability upward and where downward. </p>\n<p><em>we should do this set-by-set, but not $\\omega$-by-$\\omega$. According to following theorem</em></p>\n<p><strong>Theorem</strong> let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space and let $Z$ be an almost surely nonnegative random variable with $\\mathbb{E}Z=1$. for $A\\in\\mathcal{F}$, define $\\widetilde{\\mathbb{P}}(A)=\\int_AZ(\\omega)d\\mathbb{P}(\\omega)$. Then $\\widetilde{\\mathbb{P}}$ is a probability measure. If $X$ is a nonnegative random variable, then$\\widetilde{\\mathbb{E}}X=\\mathbb{E}[XZ]$. If $Z$ is almost surely strictly positive, we also have $\\mathbb{E}Y=\\widetilde{\\mathbb{E}}[\\frac{Y}{Z}]$ for every nonnegative random variable $Y$.</p>\n<p>PROOF</p>\n<p>$\\widetilde{\\mathbb{P}}(\\Omega)=1$, and countably additive. </p>\n<p>countably additive</p>\n<p>let $A_1,A_2,A_3,\\dots$ be a sequence of disjoint sets in $\\mathcal{F}$, and define $B_n=\\cup_{k=1}^n A_k$</p>\n<p>we can use the monotone convergence theorem, to write</p>\n<p>$$\\widetilde{\\mathbb{P}}(\\cup _{k=1}^\\infty A_k)=\\widetilde{\\mathbb{P}}(B_\\infty)=\\int_\\Omega \\mathbb{I}_{B_\\infty}(\\omega)Z(\\omega)d\\mathbb{P}(\\omega)\\\\=\\lim_{n\\to \\infty}\\int_\\Omega \\mathbb{I}_{B_n}(\\omega)Z(\\omega)d\\mathbb{P}(\\omega)\\\\=\\lim_{n\\to \\infty}\\sum\\int_\\Omega\\mathbb{I}_{A_k}(\\omega)Z(\\omega)d\\mathbb{P}(\\omega)=\\sum_{k=1}^\\infty\\widetilde{\\mathbb{P}}(A_k)$$</p>\n<p><strong>Definition</strong> 如果两个概率测度下sigma代数中零概率的集合相同,那么称两个概率测度为equivalent</p>\n<p>在金融中,实际概率测度和风险中性概率测度就是equivalent的,在risk neutral world中almost work的hedge在actual world中一定也almost surely work</p>\n<p><strong>Definition</strong> 对于equivalent的两个概率测度以及它们之间的almost surely positive random variable, 这个随机变量$Z$称之为Radon-Nikodym derivative of$\\widetilde{\\mathbb{P}}$ with respect to $\\mathbb{P}$ and we write $Z=\\frac{d\\widetilde{\\mathbb{P}}}{d\\mathbb{P}}$, $Z$ 的存在性成为Radon-Nikodym Theorem</p>\n<h1 id=\"Information-and-Conditioning\"><a href=\"#Information-and-Conditioning\" class=\"headerlink\" title=\"Information and Conditioning\"></a>Information and Conditioning</h1><h2 id=\"Information-and-sigma-algebras\"><a href=\"#Information-and-sigma-algebras\" class=\"headerlink\" title=\"Information and $\\sigma$-algebras\"></a>Information and $\\sigma$-algebras</h2><p>The hedge must specify what position we will take in the underlying security at each future time contingent on how the uncertainty between the present time and that future time is resolved.</p>\n<p><strong>resolve sets by information</strong></p>\n<p>$\\Omega$ is the set of 8 possible outcomes of 3 coin tosses,</p>\n<p>$A_H={HHH,HHT,HTH,HTT},A_T={THH,THT,TTH,TTT}$</p>\n<p>if we are told the first coin toss only. the four sets that are resolved by the first coin toss form the $\\sigma$-algebra</p>\n<p>$\\mathcal{F}_1={\\phi,\\Omega,A_H,A_T}$</p>\n<p>this $\\sigma$-algebra contains the information learned by observing the first coin toss.</p>\n<p>如果某几个集合是resolved,那么他们的并,以及各自的补也是resolved,符合$\\sigma$-algebra</p>\n<p><strong>Definition</strong> let $\\Omega$ be a nonempty set. Let $T$ be a fixed positive number and assume that for each $t\\in [0,T]$ there is a $\\sigma-algebra$ $\\mathcal{F}(t)$. Assume further that if $s\\le t$, then every set in $\\mathcal{F}(s)$ is also in $\\mathcal{F}(t)$. Then we call the collection of $\\sigma-algebra$ $\\mathcal{F}(t)$ a filtration.</p>\n<p>At time $t$ we can know whether the true $\\omega$ lies in a set in $\\mathcal{F}(t)$</p>\n<p>Let $\\Omega=C_0[0,T]$, and assign probability to the sets in $\\mathcal{F}=\\mathcal{F}(T)$, then the paths $\\omega\\in C_0[0,T]$ will be the paths of the <strong>Brownian motion</strong>.</p>\n<p><strong>Definition</strong> Let $X$ be a random variable defined on a nonempty sample space $\\Omega$. The $\\sigma-algebra$ generated by $X$, denoted $\\sigma(X)$, is the collection of all subsets of $\\Omega$ of the form ${X\\in B}$, $B$<br> <strong>ranges over</strong> the Borel subsets of $\\mathbb{R}$</p>\n<p>这里的区别和简并有点像,随机变量是本征值,Filtration是量子态</p>\n<p><strong>Definition</strong> Let $X$ be a random variable defined on a nonempty sample space $\\Omega$. Let $\\mathcal{G}$ be a $\\sigma-algebra$ of subsets of $\\Omega$. If every set in $\\sigma(X)$ is also in $\\mathcal{G}$, we say that $X$ is $\\mathcal{G}-measurable$</p>\n<p>意味着$\\mathcal{G}$ 中的信息足够决定$X$ 的值。对于borel可测函数$f$,$f(X)$也是$\\mathcal{G}-measurable$的。对于多元函数同样成立</p>\n<p><strong>Definition</strong> Let $\\Omega$ be a nonempty sample space equipped with a filtration $\\mathcal{F}(t)$. Let </p>\n<p>$X(t)$ be a collection of random variables indexed by $t\\in [0,T]$, We say this collection of random variables is an adapted stochastic process if, for each $t$, the random variable $X(t)$ is $\\mathcal{F}(t)-measurable$ </p>\n<h2 id=\"Independence\"><a href=\"#Independence\" class=\"headerlink\" title=\"Independence\"></a>Independence</h2><p>对于一个随机变量和一个$\\sigma-algebra$ $\\mathcal{G}$, measurable 和 independent 是两种极端,但大部分情况下,$\\mathcal{G}$中但信息可以估计$X$, 但不足以确定$X$的值。</p>\n<p>Independence会受到概率度量的影响,但measurability不会。</p>\n<p>probability space $(\\Omega,\\mathcal{F},\\mathbb{P})$,$\\mathcal{G}\\in \\mathcal{F}, \\mathcal{H}\\in \\mathcal{F}$, $\\Omega$ 中的两个$\\sigma-algebra$$A$和$B$独立如果$\\mathbb{P}(A\\cap B)=\\mathbb{P}(A)\\cdot\\mathbb{P}(B)$, for all $A\\in \\mathcal{G},B\\in \\mathcal{H}$</p>\n<p>独立的定义可以拓展到随机变量($\\sigma-algebra$ they generate are independent)之间,随机变量与$\\sigma-algebra$之间。</p>\n<p><strong>Definition</strong> $(\\Omega,\\mathcal{F},\\mathbb{P})$ is a probability space and let $\\mathcal{G}_1,\\mathcal{G}_2,\\mathcal{G}_3\\dots$ be a sequence of $sub-\\sigma-algebra$ of $\\mathcal{F}$. For a fixed positive integer n, we say that the n $\\sigma-algebra$s $\\mathcal{G}_1,\\mathcal{G}_2,\\mathcal{G}_3\\dots\\mathcal{G}_n$ are independent if$\\mathbb{P}(A_1\\cap A_2\\cap \\dots\\cap A_n)=\\mathbb{P}<br>(A_1)\\mathbb{P}<br>(A_2)\\dots \\mathbb{P}<br>(A_n)$ for all $A_i\\in \\mathcal{G}_i$</p>\n<p>这个同样也可以拓展到随机变量之间以及随机变量与$\\sigma-algebra$之间。</p>\n<p><strong>Theorem</strong> Let $X$ and $Y$ be independent random variables, and let $f$ and $g$ be Borel measurable functions on $\\mathbb{R}$. Then$f(X)$ and $g(Y)$ are independent random variables.</p>\n<p>PROOF</p>\n<p>Let $A$ be in the $\\sigma-algebra$ generated by $f(X)$. This $\\sigma-algebra$ is a $sub-\\sigma -algebra$ of $\\sigma(X)$. </p>\n<p>这很自然,every set in $A$ is of the form${\\omega \\in \\Omega;f(X(\\omega))\\in C}\\text{,where }C\\text{ is a Borel subset of }\\mathbb{R}$. 只需要定义$D={x\\in \\mathbb{R};f(x)\\in C}$. Then we know$A\\in \\sigma(X)$. Let $B$ be the $\\sigma-algebra$ gnenerated by $g(Y)$, then $B\\in \\sigma(Y)$. 由于$X,Y$独立,所以$A,B$独立。</p>\n<p><strong>Definition</strong> Let$X$ and $Y$ be random variables. The pair of random variables$(X,Y)$ takes values in the plane$\\mathbb{R}^2$, and the joint distribution measure of $(X,Y)$ is given by$\\mu_{X,Y}(C)=\\mathbb{P}{(X,Y)\\in C}$ for all Borel sets $C\\in \\mathbb{R}^2$</p>\n<p>同样满足概率度量的两个条件:全空间测度为1,以及countable additivity preperty</p>\n<p><strong>Theorem</strong> Let $X$ and $Y$ be random variables. The following conditions and equivalent.</p>\n<ol>\n<li><p>$X$ and $Y$ are independent</p>\n</li>\n<li><p>the joint distribution measure factors:</p>\n<p> $\\mu_{X,Y}(A\\times B)=\\mu_X(A)\\mu_Y(B)$ for all Borel subsets$A\\in \\mathbb{R},B\\in\\mathbb{R}$</p>\n</li>\n<li><p>the joint cumulative distribution function factors</p>\n<p> $F_{X,Y}(a,b)=F_X(a)F_Y(b)$ for all $a\\in \\mathbb{R},b\\in \\mathbb{R}$</p>\n</li>\n<li><p>the joint moment-generating function factor:(矩母函数)</p>\n<p> $\\mathbb{E}e^{uX+vY}=\\mathbb{E}e^{uX}\\cdot\\mathbb{E}e^{vY}$</p>\n</li>\n<li><p>the joint density factors(if there is one)</p>\n<p> $f_{X,Y}(x,y)=f_X(x)f_Y(y)$ for almost every$x\\in\\mathbb{R},y\\in\\mathbb{R}$</p>\n</li>\n</ol>\n<p>conditions above imply but are not equivalent to:</p>\n<ol>\n<li>$\\mathbb{E}[XY]=\\mathbb{E}X\\cdot\\mathbb{E}Y$ provided $\\mathbb{E}|XY|<\\infty$</li>\n</ol>\n<p><strong>Definition</strong> Let $X$ be a random variable whose expected value is defined. The variance of $X$, denoted $Var(X)$ is $Var(X)=\\mathbb{E}[(X-\\mathbb{E}X)^2]=\\mathbb{E}[X^2]-(\\mathbb{E}X)^2$</p>\n<p>covariance of $X$ and $Y$ is $Cov(X,Y)=\\mathbb{E}[(X-\\mathbb{E}X)(Y-\\mathbb{E}Y)]=\\mathbb{E}[XY]-\\mathbb{E}X\\cdot\\mathbb{E}Y$</p>\n<p>correlation coefficient of $X$and $Y$ is $\\rho(X,Y)=\\frac{Cov(X,Y)}{\\sqrt{Var(X)Var(Y)}}$</p>\n<p>if $\\rho(X,Y)=0$, we say that $X$ and $Y$ are uncorrelated</p>\n<h2 id=\"General-Conditional-Expectations\"><a href=\"#General-Conditional-Expectations\" class=\"headerlink\" title=\"General Conditional Expectations\"></a>General Conditional Expectations</h2><p><strong>Definition</strong> Let$(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space, let $\\mathcal{G}$ be a sub-$\\sigma$-algebra of $\\mathcal{F}$, and let $X$ be a random variable that is either nonnegative or integrable. The conditional expectation of $X$ given $\\mathcal{G}$, denoted$\\mathbb{E}[X|\\mathcal{G}]$, is any random variable that satisfies</p>\n<ol>\n<li><strong>Measurability $\\mathbb{E}[X|\\mathcal{G}]$</strong> is $\\mathcal{G}$ measurable</li>\n<li><strong>Partial averaging $\\int_A\\mathbb{E}[X|\\mathcal{G}(\\omega)]=\\int_AX(\\omega)d\\mathbb{P}(\\omega)$</strong> for all $A\\in \\mathcal{G}$</li>\n</ol>\n<p>If $\\mathcal{G}$ is generated by some other random variable $W$, then we can write$\\mathbb{E}[X|W]$</p>\n<p>(1) means although the estimate of $X$based on the information in $\\mathcal{G}$ is itself a random variable, the value of the estimate $\\mathbb{E}[X|\\mathcal{G}]$ can be determined from the information in $\\mathcal{G}$</p>\n<p>存在性可以由Radon-Nikodym Theorem证明</p>\n<p>唯一性的证明如下:If $Y$ and $Z$ both satisfy conditions, then their difference $Y-Z$ is as well, and thus the set $A={Y-Z>0}$ is in $\\mathcal{G}$. 根据(2),$\\int_AY(\\omega)d\\mathbb{P}(\\omega)=\\int_AX(\\omega)d\\mathbb{P}(\\omega)=\\int_AZ(\\omega)d\\mathbb{P}(\\omega)$</p>\n<p>Hence $Y=Z$ almost surely.</p>\n<p><strong>Theorem</strong> Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space and let $\\mathcal{G}$ be a sub-$\\sigma$-algebra of $\\mathcal{F}$</p>\n<ol>\n<li><p>linearity of conditional expectations<br>$\\mathbb{E}[c_1X+c_2Y|\\mathcal{G}]=c_1\\mathbb{E}[X|\\mathcal{G}]+c_2\\mathbb{E}[Y|\\mathcal{G}]$</p>\n</li>\n<li><p>taking out what is known. </p>\n<p> If $X$ is $\\mathcal{G}$-measurable</p>\n<p> $\\mathbb{E}[XY|\\mathcal{G}]=X\\mathbb{E}[Y|\\mathcal{G}]$</p>\n</li>\n<li><p>iterated conditioning.</p>\n<p> If $\\mathcal{H}$ is a sub-$\\sigma$-algebra of $\\mathcal{G}$ and $X$ is an integrable random variable, then</p>\n<p> $\\mathbb{E}[\\mathbb{E}[X|\\mathcal{G}]|\\mathcal{H}]=\\mathbb{E}[X|\\mathcal{H}]$</p>\n</li>\n<li><p>independence</p>\n<p> If $X$ is independent of $\\mathcal{G}$, then $\\mathbb{E}[X|\\mathcal{G}]=\\mathbb{E}X$</p>\n</li>\n<li><p>conditional Jensen’s inequality</p>\n<p> $\\mathbb{E}[\\phi(X)|\\mathcal{G}]\\ge\\phi(\\mathbb{E}[X|\\mathcal{G}])$</p>\n</li>\n</ol>\n<p><strong>Lemma</strong> Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space, and let $\\mathcal{G}$ be a sub-$\\sigma$-algebra of $\\mathcal{F}$. Suppose the random variables $X_1,\\dots,X_K$ are $\\mathcal{G}$-measurable and the random variables$Y_1,\\dots,Y_L$ are independent of $\\mathcal{G}$. Let $f(x_1,\\dots,x_K,y_1,\\dots,y_L)$ be a function of the dummy variables, and define: </p>\n<p>$g(x_1,\\dots,x_K)=\\mathbb{E}f(x1,\\dots,x_K,Y_1,\\dots,Y_L)$</p>\n<p>This means holding $X_i$ constant and integrate out $Y_i$.</p>\n<p>Then,$\\mathbb{E}[f(X_1,\\dots,X_K,Y_1,\\dots,Y_L)|\\mathcal{G}]=g(X_1,\\dots,X_K)$</p>\n<p><strong>Definition</strong> Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space, let $T$ be a fixed positive number, and let $\\mathcal{F}(t)$, $0\\le t\\le T$, be a filtration of $sub-\\sigma-algebra$ of $\\mathcal{F}$. Consider an adapted stochastic process $M(t)$:</p>\n<ol>\n<li>If $\\mathbb{E}[M(t)|\\mathcal{F}(s)]=M(s)$ for all $0\\le s\\le t \\le T$, this process is a <em><strong>martingale</strong></em>. It has no tendency to rise or fall.</li>\n<li>If $\\mathbb{E}[M(t)|\\mathcal{F}(s)]\\le M(s)$ for all $0\\le s\\le t \\le T$, this process is a <em><strong>supermartingale</strong></em>. It has no tendency to rise, it may have a tendency to fall.</li>\n<li>If $\\mathbb{E}[M(t)|\\mathcal{F}(s)]\\ge M(s)$ for all $0\\le s\\le t \\le T$, this process is a <em><strong>submartingale</strong></em>. It has no tendency to fall, it may have a tendency to rise.</li>\n</ol>\n<p><strong>Definition</strong> Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space, let $T$ be a fixed positive number, and let $\\mathcal{F}(t)$, $0\\le t\\le T$, be a filtration of $sub-\\sigma-algebra$ of $\\mathcal{F}$. Consider an adapted stochastic process $X(t)$. Assume that for all $0\\le s\\le t\\le T$ and for every nonnegative, Borel-measuable function $f$, there is another Borel-measuable function $g$ such that:</p>\n<p>$\\mathbb{E}[f(X(t))|\\mathcal{F}(s)]=g(X(s))$</p>\n<p>Then we say that the X is a Markov process</p>\n<h1 id=\"Brownian-Motion\"><a href=\"#Brownian-Motion\" class=\"headerlink\" title=\"Brownian Motion\"></a>Brownian Motion</h1><h2 id=\"Scaled-Random-Walks\"><a href=\"#Scaled-Random-Walks\" class=\"headerlink\" title=\"Scaled Random Walks\"></a>Scaled Random Walks</h2><h3 id=\"Symmetric-Random-Walk\"><a href=\"#Symmetric-Random-Walk\" class=\"headerlink\" title=\"Symmetric Random Walk\"></a>Symmetric Random Walk</h3><p>To build a <strong>symmetric random walk</strong> we repeatedly toss a fair coin.</p>\n<p>$X_j=\\begin{cases}1 \\text{ if }\\omega_j=H\\\\-1\\text{ if }\\omega_j=T\\end{cases}$</p>\n<p>$M_0=0$, $M_k=\\sum_{j=1}^kX_j$</p>\n<p>the process $M_k$ is a <em>symmetric random walk.</em></p>\n<h3 id=\"Increments-of-the-Symmetric-Random-Walk\"><a href=\"#Increments-of-the-Symmetric-Random-Walk\" class=\"headerlink\" title=\"Increments of the Symmetric Random Walk\"></a>Increments of the Symmetric Random Walk</h3><p>A random walk has independent increments(独立增量性)</p>\n<p>if we choose nonnegative integers$0=k_0<k_1<\\cdots<k_m$ , the random variables $M_{k_i}-M_{k_{i-1}}$ are independent.</p>\n<p>Each of these random variables $M_{k_i}-M_{k_{i-1}}=\\sum_{j=k_{i+1}}^{k_{i+1}}X_j$ is called an increment of the random walk. </p>\n<p>Each increment has expected value 0 and variance $k_{i+1}-k_i$ . The variance is obvious because $X_j$ are independent.</p>\n<h3 id=\"Martingale-Property-for-the-Symmetric-Random-Walk\"><a href=\"#Martingale-Property-for-the-Symmetric-Random-Walk\" class=\"headerlink\" title=\"Martingale Property for the Symmetric Random Walk\"></a>Martingale Property for the Symmetric Random Walk</h3><p>We choose nonnegative integers $k<l$ and compute:</p>\n<p>$\\mathbb{E}[M_l|\\mathcal{F}_k]=\\mathbb{E}[(M_l-M_k)+M_k|\\mathcal{F}_k]=\\mathbb{E}[M_l-M_k|\\mathcal{F}_k]+\\mathbb{E}[M_k|\\mathcal{F}_k]=M_k$</p>\n<h3 id=\"Quadratic-Variation-of-the-Symmetric-Random-Walk\"><a href=\"#Quadratic-Variation-of-the-Symmetric-Random-Walk\" class=\"headerlink\" title=\"Quadratic Variation of the Symmetric Random Walk\"></a>Quadratic Variation of the Symmetric Random Walk</h3><p>the quadratic variation up to time $k$ is defined to be $[M,M]_k=\\sum_{j=1}^k(M_j-M_{j-1})^2=k$</p>\n<p>This is computed path-by-path. taking all the one step increments $M_j-M_{j-1}$ along that path, squaring these increments, and then summing them.</p>\n<p>Note that $[M,M]_k$ is the same as $Var(M_k)$, but the computations of these two quantities are quite different. $Var$ is computed by taking an average over all paths, taking their probability into account. If the random walk is not symmetric, the probability distribution would affect $Var$. On the contrary, the probability up and down do not affect the quadratic variation computation.</p>\n<h3 id=\"Scaled-Symmetric-Random-Walk\"><a href=\"#Scaled-Symmetric-Random-Walk\" class=\"headerlink\" title=\"Scaled Symmetric Random Walk\"></a>Scaled Symmetric Random Walk</h3><p>We fix a positive integer $n$ and define the <strong>scaled symmetric random walk</strong> $W^{(n)}(t)=\\frac{1}{\\sqrt{n}}M_{nt}$. If $nt$ is not an integer, we define $W^{(n)}(t)$ by linear interpolation between its values at the nearest points $s$ and $u$ to the left and right of $t$ for which $ns$ and $nu$ are integers. </p>\n<p>A Brownian motion is a scaled symmetric random walk with $n\\to \\infty$</p>\n<p>$\\mathbb{E}(W^{(n)}(t)-W^{(n)}(s))=0,Var(W^{(n)}(t)-W^{(n)}(s))=t-s$</p>\n<p>Let $0\\le s\\le t$ be given, and decompose $W^{(n)}(t)$ as: $W^{(n)}(t)=(W^{(n)}(t)-W^{(n)}(s))+W^{(n)}(s)$ </p>\n<p>$(W^{(n)}(t)-W^{(n)}(s))$ is independent of $\\mathcal{F}(s)$, the $\\sigma-algebra$ of information available at time s, and $W^{(n)}(s)$ is $\\mathcal{F}(s)$ measurable. So $\\mathbb{E}[W^{(n)}(t)|\\mathcal{F}(s)]=W^{(n)}(s)$</p>\n<p>The <strong>quadratic variation</strong> of the scaled random walk: </p>\n<p>$[W^{(n)},W^{(n)}](t)=\\sum_{j=1}^{nt}[W^{(n)}(\\frac{j}{n})-W^{(n)}(\\frac{j-1}{n})]^2=\\sum_{j=1}^{nt}[W^{(n)}[\\frac{1}{\\sqrt{n}}X_j]^2=\\sum_{j=1}^{nt}\\frac{1}{n}=t$</p>\n<h3 id=\"Limiting-Distribution-of-the-Scaled-Random-Walk\"><a href=\"#Limiting-Distribution-of-the-Scaled-Random-Walk\" class=\"headerlink\" title=\"Limiting Distribution of the Scaled Random Walk\"></a>Limiting Distribution of the Scaled Random Walk</h3><p><strong>Theorem: Central limit</strong> Fix $t\\ge 0$. As $n\\to \\infty$, the distribution of the scaled random walk $W^{(n)}(t)$ evaluated at time $t$ converges to the normal distribution with mean zero and variance $t$.</p>\n<p>PROOF</p>\n<p>For the normal density $f(s)=\\frac{1}{\\sqrt{2\\pi t}}e^{-\\frac{x^2}{2t}}$, the moment-generating function is </p>\n<p>$\\phi(u)=\\frac{1}{\\sqrt{2\\pi t}}\\int_{-\\infty}^\\infty \\exp{ux-\\frac{x^2}{2t}}dx=e^{\\frac{1}{2}u^2t}$</p>\n<p>If $t$ is such that $nt$ is an integer, then the moment-generating function for $W^{(n)}(t)$ is:</p>\n<p>$\\phi_n(u)=\\mathbb{E}e^{uW^{(n)}(t)}=\\mathbb{E}\\exp{\\frac{u}{\\sqrt{n}}M_{nt}}=\\mathbb{E}\\exp{\\frac{u}{\\sqrt{n}}\\sum_{j=1}^{nt}X_j}=\\mathbb{E}\\prod_{j=1}^{nt}\\exp{\\frac{u}{\\sqrt{n}}X_j}\\\\=\\prod_{j=1}^{nt}\\mathbb{E}\\exp{\\frac{u}{\\sqrt{n}}X_j}=\\prod_{j=1}^{nt}(\\frac{e^{\\frac{u}{\\sqrt{n}}}+e^{\\frac{-u}{\\sqrt{n}}}}{2})=(\\frac{e^{\\frac{u}{\\sqrt{n}}}+e^{\\frac{-u}{\\sqrt{n}}}}{2})^{nt}$</p>\n<p>when $n\\to \\infty$ , $\\phi(u)=e^{\\frac{1}{2}u^2t}$</p>\n<h3 id=\"Log-Normal-Distribution-as-the-Limit-of-the-Binomial-Model\"><a href=\"#Log-Normal-Distribution-as-the-Limit-of-the-Binomial-Model\" class=\"headerlink\" title=\"Log-Normal Distribution as the Limit of the Binomial Model\"></a>Log-Normal Distribution as the Limit of the Binomial Model</h3><p>We build a model for a stock price on the time interval from $0$ to $t$ by choosing an integer $n$ and constructing a binomial model for the stock price that takes $n$ steps per unit time. Up factor $u_n=1+\\frac{\\sigma}{\\sqrt{n}}$, down factor $u_d=1-\\frac{\\sigma}{\\sqrt{n}}$. $r=0.$</p>\n<p>The risk-neutral probabilities are then:</p>\n<p>$\\tilde{p}=\\frac{1+r-d_n}{u_n-d_n}=\\frac{1}{2}$, $\\tilde{q}=\\frac{u_n-1-r}{u_n-d_n}=\\frac{\\sigma/\\sqrt{n}}{2\\sigma/\\sqrt{n}}=\\frac{1}{2}$</p>\n<p>Random walk $M_{nt}=H_{nt}-T_{nt}$, while $nt=H_{nt}+T_{nt}$</p>\n<p>the stock price at time $t$ is $S_n(t)=S(0)u_n^{H_{nt}}d_n^{T_{nt}}=S(0)(1+\\frac{\\sigma}{\\sqrt{n}})^{\\frac{1}{2}(nt+M_{nt})}(1+\\frac{\\sigma}{\\sqrt{n}})^{\\frac{1}{2}(nt+M_{nt})}(1-\\frac{\\sigma}{\\sqrt{n}})^{\\frac{1}{2}(nt-M_{nt})}$</p>\n<p>we need to identify the distribution of this random variable as $n\\to \\infty$</p>\n<p><strong>Theorem</strong> As $n\\to \\infty$ , the distribution of $S_n(t)$ converges to the distribution of</p>\n<p>$S(t)=S(0)\\exp{\\sigma W(t)-\\frac{1}{2}\\sigma^2t}$ </p>\n<p>$W(t)$ is a normal random variable with mean zero and variance $t$</p>\n<p>PROOF:</p>\n<p>$\\log S_n(t)\\\\=\\log S(0)+\\frac{1}{2}(nt+M_{nt})\\log (1+\\frac{\\sigma}{\\sqrt{n}})+\\frac{1}{2}(nt-M_{nt})\\log (1-\\frac{\\sigma}{\\sqrt{n}})\\\\=\\log S(0)+\\frac{1}{2}(nt+M_{nt})(\\frac{\\sigma}{\\sqrt{n}}-\\frac{\\sigma^2}{2n}+O(n^{-3/2}))+\\frac{1}{2}(nt-M_{nt})(\\frac{\\sigma}{-\\sqrt{n}}-\\frac{\\sigma^2}{2n}+O(n^{-3/2}))\\\\=\\log S(0)+nt(-\\frac{\\sigma^2}{2n}+O(n^{-3/2}))+M_{nt}(\\frac{\\sigma}{\\sqrt{n}}+O(n^{-3/2}))=\\log S(0)-\\frac{1}{2}\\sigma^2t+\\sigma W^{(n)}(t)$</p>\n<p>By the <strong>Central Limit Theorem,</strong> we know that $\\frac{1}{\\sqrt{n}}M_{nt}=W^{(n)}(t)\\to W(t), \\text{when }n\\to \\infty$</p>\n<h2 id=\"Brownian-Motion-1\"><a href=\"#Brownian-Motion-1\" class=\"headerlink\" title=\"Brownian Motion\"></a>Brownian Motion</h2><h3 id=\"Definition-of-Brownian-Motion\"><a href=\"#Definition-of-Brownian-Motion\" class=\"headerlink\" title=\"Definition of Brownian Motion\"></a>Definition of Brownian Motion</h3><p><strong>Definition</strong> Let $(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space. For each $\\omega\\in\\Omega$, suppose there is a continuous function $W(t)$ of $t\\ge 0$ that satisfies $W(0)=0$ that depends on $\\omega$. Then $W(t),t\\ge 0$ is a Brownian motion if for all $t_i$ the increments $W(t_i)-W(t_{i-1})$ are independent and each of these increments is normally distributed with $\\mathbb{E}[W(t_{i+1})-W(t_i)]=0,Var[W(t_{i+1})-W(t_i)]=t_{i+1}-t_i$</p>\n<p>Difference between BM and a scaled random walk: the scaled random walk has a natural time step and is linear between these time steps, whereas the BM has no linear pieces.</p>\n<h3 id=\"Distribution-of-Brownian-Motion\"><a href=\"#Distribution-of-Brownian-Motion\" class=\"headerlink\" title=\"Distribution of Brownian Motion\"></a>Distribution of Brownian Motion</h3><p>For any two times, the covariance of $W(s)$ and $W(t)$ for $s\\le t$ is</p>\n<p>$\\mathbb{E}[W(s)W(t)]=\\mathbb{E}[W(s)(W(t)-W(s))+W^2(s)]=\\mathbb{E}[W(s)]\\mathbb{E}[(W(t)-W(s))]+\\mathbb{E}[W^2(s)]=s$</p>\n<p>We compute the moment-generating function of the random vector$(W(t_1),W(t_2),\\dots,W(t_m))$</p>\n<p>$\\phi=\\mathbb{E}\\exp{u_mW(t_m)+\\dots+u_1W(t_1)}=\\mathbb{E}\\exp{u_m(W(t_m)-W(t_{m-1}))+\\dots+(u_1+u_2+\\dots+u_m)W(t_1)}=\\mathbb{E}\\exp{u_m(W(t_m)-W(t_{m-1}))}\\cdots \\mathbb{E}\\exp{(u_1+u_2+\\cdots+u_m)W(t_1)}=\\exp{\\frac{1}{2}u_m^2(t_m-t_{m-1})}\\cdots\\exp{(u_1+u_2+\\cdots+u_m)^2t_1}$</p>\n<p>The distribution of the Brownian increments can be specified by specifying the joint density or the joint moment-generating function of the random variables</p>\n<p><strong>Theorem</strong> Let$(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space. For each $\\omega\\in\\Omega$, suppose there is a continuous function $W(t)$ of $t\\ge 0$ that satisfies $W(0)=0$ and that depends on $\\omega$. </p>\n<ol>\n<li><p>For all $0< t_0< t_1\\cdots <t_m$, the increments are independent and each of these increments is normally distributed with mean and variance given by$\\mathbb{E}[W(t_{i+1})-W(t_i)]=0,Var[W(t_{i+1})-W(t_i)]=t_{i+1}-t_i$</p>\n</li>\n<li><p>For all $0< t_0< t_1\\cdots <t_m$, the random variables $W(t_i)$ are jointly normally distributed with means equal to zero and covariance matrix</p>\n<p> $\\begin{pmatrix} t_{1} &t_1 \\cdots & t_{1} \\\\ t_1&t_2\\cdots &t_2\\\\ \\vdots & \\ddots & \\vdots \\\\ t_{1} &t_2 \\cdots & t_{m} \\end{pmatrix}$ </p>\n</li>\n<li><p>the random variables have the joint moment-generating function mentioned before</p>\n</li>\n</ol>\n<h3 id=\"Filtration-for-Brownian-Motion\"><a href=\"#Filtration-for-Brownian-Motion\" class=\"headerlink\" title=\"Filtration for Brownian Motion\"></a>Filtration for Brownian Motion</h3><p><strong>Definition</strong> Let$(\\Omega,\\mathcal{F},\\mathbb{P})$ be a probability space on which is defined a Brownian motion $W(t),t\\ge 0$. A filtration for the Brownian motion is a collection of $\\sigma$-algebra $\\mathcal{F}(t),t\\ge 0$, satisfying:</p>\n<ol>\n<li><strong>Information accumulates</strong></li>\n<li><strong>Adaptivity: $W(t)$</strong> is <strong>$\\mathcal{F}(t)$</strong>-measurable</li>\n<li><strong>Independence of future increments</strong></li>\n</ol>\n<p>$\\Delta(t),t\\ge0$, be a stochastic process. $\\Delta(t)$ is adapted to the filtration $\\mathcal{F}(t)$ if for each $t\\ge 0$ the random variable $\\Delta(t)$ if $\\mathcal{F}(t)$-measurable.</p>\n<p>There are two possibilities for the filtration $\\mathcal{F}(t)$ for a Brownian motion. </p>\n<ol>\n<li>to let $\\mathcal{F}(t)$ contain only the info obtained by observing the BM itself up to time $t$. </li>\n<li>to include in $\\mathcal{F}(t)$ info obtained by observing the BM and one or more other processes. But if the info in $\\mathcal{F}(t)$ includes observations of processes other than the BM $W$, this additional info is not allowed to give clues about the future increments because of property iii</li>\n</ol>\n<h3 id=\"Martingale-Property-for-Brownian-Motion\"><a href=\"#Martingale-Property-for-Brownian-Motion\" class=\"headerlink\" title=\"Martingale Property for Brownian Motion\"></a>Martingale Property for Brownian Motion</h3><p><strong>Theorem</strong> Brownian motion is a martingale</p>\n<h2 id=\"Quadratic-Variation\"><a href=\"#Quadratic-Variation\" class=\"headerlink\" title=\"Quadratic Variation\"></a>Quadratic Variation</h2><p>For BM, there is no natural step size. If we are given $T>0$, we could simply choose a step size, say $\\frac{T}{n}$ for some large $n$, and compute the quadratic variation up to time $T$ with this step size:</p>\n<p>$\\sum_{j=0}^{n-1}[W(\\frac{(j+1)T}{n})-W(\\frac{jT}{n})]^2$</p>\n<p>The variation of paths of BM is not zero, which makes stochastic calculus different from ordinary calculus</p>\n<h3 id=\"First-Order-Variation\"><a href=\"#First-Order-Variation\" class=\"headerlink\" title=\"First-Order Variation\"></a>First-Order Variation</h3><p>$FV_T(f)=|f(t_1)-f(0)|+|f(t_2)-f(t_1)|+\\dots+|f(T)-f(t_2)|=\\int_0^{t_1}f’(t)dt+\\dots+\\int_{t_2}^Tf’(t)dt=\\int_0^T|f’(t)|dt$</p>\n<p>We first choose a partition $\\Pi={t_0,t_1,\\dots,t_n}$ of $[0,T]$, which is a set of times. These will serve to determine the step size. The maximum step size of the partition will be denoted $\\Vert\\Pi\\Vert=\\max_{j=0,\\dots,n-1}(t_{j+1}-t_j)$. We then define:</p>\n<p>$FV_T(f)=\\lim_{\\Vert\\Pi\\Vert\\to0}\\sum_{j=0}^{n-1}\\vert f(t_{j+1})-f(t_j)\\vert$</p>\n<p>用中值定理可以证明与积分相等</p>\n<h3 id=\"Quadratic-Variation-1\"><a href=\"#Quadratic-Variation-1\" class=\"headerlink\" title=\"Quadratic Variation\"></a>Quadratic Variation</h3><p><strong>Definition</strong> Let $f(t)$ be a function defined for $0\\le t\\le T$. The quadratic variation to $f$ up to time $T$ is </p>\n<p>$[f,f](T)=\\lim_{\\Vert\\Pi\\Vert\\to0}\\sum_{j=0}^{n-1}\\vert f(t_{j+1})-f(t_j)\\vert$</p>\n<p>if $f$ is derivative, then $<a href=\"T\">f,f</a>=0$</p>\n<p>if $\\int_0^T\\vert f’(t^*_j)\\vert ^2dt$ is infinite, then $[f,f](T)$ lead to a $0\\cdot\\infty$ situation, which can be anything between $0$ and $\\infty$</p>\n<p><strong>Theorem</strong> Let $W$ be a Brownian motion. Then $[W,W](T)=T$ for all $T\\ge 0$ almost surely.</p>\n<p>PROOF</p>\n<p>Define the <em>sample quadratic variation</em> corresponding to the partition of $[0,T]$, $\\Pi ={t_0,t_1,\\dots,t_n}$ to be</p>\n<p> $Q_\\Pi=\\sum_{j=0}^{n-1}(W(t_{j+1})-W(t_j))^2$</p>\n<p>We can show that $Q_\\Pi$ converges to $T$ as $\\Vert\\Pi\\Vert\\to0$</p>\n<p>$\\mathbb{E}[(W(t_{j+1})-W(t_j))^2]=Var[W(t_{j+1})-W(t_j)]=t_{j+1}-t_j$ implies:</p>\n<p>$\\mathbb{E}Q_\\Pi=\\sum\\mathbb{E}[(W(t_{j+1})-W(t_j))^2]=\\sum(t_{j+1}-t_j)=T$</p>\n<p>$Var[(W(t_{j+1})-W(t_j))^2]=\\mathbb{E}[(W(t_{j+1})-W(t_j))^4]-2(t_{j+1}-t_j)\\mathbb{E}[(W(t_{j+1})-W(t_j))^2]+(t_{j+1}-t_j)^2$</p>\n<p>$\\mathbb{E}[(W(t_{j+1})-W(t_j))^4]=3(t_{j+1}-t_j)^2$,$\\mathbb{E}[(W(t_{j+1})-W(t_j))^2]=t_{j+1}-t_j$</p>\n<p>PROOF</p>\n<p>By Ito’s formula, we have</p>\n<p>$𝑊^4(t)=4\\int^𝑡_0𝑊^3_s𝑑𝑊_s+6\\int^𝑡_0𝑊^2_sds$</p>\n<p>$M(t):=\\int_0^tW_s^3dW_s=0$ is a martingale and $\\mathbb{E}M(t)=\\mathbb{E}M(0)=0$</p>\n<p>$\\mathbb{E}W^4(t)=6\\int_0^t\\mathbb{E}[W_s^2]ds=6\\int_0^tsds=3t^2$</p>\n<p>so $Var[(W(t_{j+1}-W(t_j))^4]=2(t_{j+1}-t_j)^2$</p>\n<p>and $Var(Q_\\Pi)=\\sum 2(t_{j+1}-t_j)^2\\le2\\Vert\\Pi\\Vert T$</p>\n<p>In particular, $\\lim_{\\Vert\\Pi\\Vert\\to 0}Var(Q_\\Pi)=0,lim_{\\Vert\\Pi\\Vert\\to0}Q_\\Pi=\\mathbb{E}Q_\\Pi=T$</p>\n<p>$(W(t_{j+1})-W(t_j))^2\\approx t_{j+1}-t_j$$(W(t_{j+1})-W(t_j))^2=t_{j+1}-t_j$ when $t_{j+1}-t_j$ is very small</p>\n<p>$dW(t)dW(t)=dt$ is the informal write</p>\n<p>$dWdt=0,dtdt=0$</p>\n<h3 id=\"Volatility-of-Geometric-Brownian-Motion\"><a href=\"#Volatility-of-Geometric-Brownian-Motion\" class=\"headerlink\" title=\"Volatility of Geometric Brownian Motion\"></a>Volatility of Geometric Brownian Motion</h3><p>geometric Brownian motion: $S(t)=S(0)\\exp{\\sigma W(t)+(\\alpha-\\frac{1}{2}\\sigma^2)t}$</p>\n<p>realized volatility: the sum of the squares of the log returns</p>\n<p>for $T_1=t_0<t_1<\\cdots<tm=T_2$,</p>\n<p>$\\sum (\\log\\frac{S(t_{j+1})}{S(t_j)})^2=\\sigma^2\\sum(W(t_{j+1})-W(t_j))^2+(\\alpha-\\frac{1}{2}\\sigma^2)^2\\sum(t_{j+1}-t_j)^2+2\\sigma (\\alpha-\\frac{1}{2}\\sigma^2)\\sum(W(t_{j+1})-W(t_j))(t_{j+1}-t_j)$</p>\n<p>When the maximum step size $\\Vert\\Pi\\Vert=\\max_{j=0,1,\\dots,m-1}(t_{j+1}-t_j)$ is small, then the first term is approximately equal to its limit $\\sigma^2(T_2-T_1)$,hence, we have:</p>\n<p>$\\frac{1}{T_2-T_1}\\sum(\\log\\frac{S(t_{j+1})}{S(t_j)})^2\\approx\\sigma^2$</p>\n<h2 id=\"Markov-Property\"><a href=\"#Markov-Property\" class=\"headerlink\" title=\"Markov Property\"></a>Markov Property</h2><p><strong>Theorem</strong> Let$W(t),t\\ge0$, be a Brownian motion and let $\\mathcal{F}(t),t\\ge0$ Be a filtration for this Brownian motion. Then $W(t)$ is a Markov process</p>\n<p>PROOF</p>\n<p>We need to show: $\\mathbb{E}[f(W(t))\\vert \\mathcal{F}(s)]=g(W(s))$ $g$ Exists whenever given $0\\le s\\le t,f$</p>\n<p>$\\mathbb{E}[f(W(t))\\vert\\mathcal{F}(s)]=\\mathbb{E}[f((W(t)-W(s))+W(s))\\vert\\mathcal{F}(s)]$</p>\n<p>$W(t)-W(s)$ is normally distributed with mean zero and variance $t-s$</p>\n<p>Replace $W(s)$ with a dummy variable $x$<br>, define $g(x)=\\mathbb{E}f(W(t)-W(s)+x)$, then </p>\n<p>$g(x)=\\frac{1}{\\sqrt{2\\pi(t-s)}}\\int f(w+x)\\exp{-\\frac{w^2}{2(t-s)}}dw=\\frac{1}{\\sqrt{2\\pi\\tau}}\\int f(y)\\exp{-\\frac{(y-x)^2}{2\\tau}}dy$</p>\n<p>Define the <em>transition density $p(\\tau,x,y):=\\frac{1}{\\sqrt{2\\pi\\tau}}e^{-\\frac{(y-x)^2}{2\\tau}},\\tau=t-s$</em></p>\n<p>$g(x)=\\int f(y)p(\\tau,x,y)dy$ </p>\n<p>And $\\mathbb{E}[f(W(t))\\vert\\mathcal{F}(s)]=\\int f(y)p(\\tau,W(s),y)dy$</p>\n<p>Conditioned on the information in $\\mathcal{F}(s)$, the conditional density of $W(t)$ is $p(\\tau,W(s),y)$. This is a density in the variable $y$, normal with mean $W(s)$ and variance $\\tau$. The only information from $\\mathcal{F}(s)$ that is relevant is the value of $W(s)$</p>\n<h2 id=\"First-Passage-Time-Distribution\"><a href=\"#First-Passage-Time-Distribution\" class=\"headerlink\" title=\"First Passage Time Distribution\"></a>First Passage Time Distribution</h2><p>exponential martingale corresponding to $\\sigma$: $Z(t)=\\exp{\\sigma W(t)-\\frac{1}{2}\\sigma^2t}$</p>\n<p><strong>Theorem</strong> Exponential martingale Let $W(t),t\\ge 0$, be a Brownian motion with a filtration $\\mathcal{F}(t),t\\ge 0$, and let $\\sigma$ be a constant, thew process $Z(t)$ is a martingale</p>\n<p>PROOF</p>\n<p>$\\mathbb{E}[Z(t)\\vert\\mathcal{F}(s)]=\\mathbb{E}[\\exp{\\sigma W(t)-\\frac{1}{2}\\sigma^2t}\\vert \\mathcal{F}(s)]=\\mathbb{E}[\\exp{\\sigma (W(t)-W(s))}\\cdot\\exp{\\sigma W(s)-\\frac{1}{2}\\sigma^2t}\\vert \\mathcal{F}(s)]=\\exp{\\sigma W(s)-\\frac{1}{2}\\sigma^2t}\\cdot\\mathbb{E}[\\exp{\\sigma (W(t)-W(s))}]$</p>\n<p>$W(t)-W(s)$ is a normal distribution with mean zero and variance $\\sigma$ so $\\mathbb{E}[\\exp{\\sigma (W(t)-W(s))}]=\\frac{1}{2}\\sigma^2(t-s)$</p>\n<p>$\\mathbb{E}[Z(t)\\vert\\mathcal{F}(s)]=Z(s)$</p>\n<p>Let $m$ be a real number, and define the first passage time to level $m$: $\\tau_m=\\min{t\\ge 0;W(t)=m}$ if the BM never reaches the level $m$, we set $\\tau_m=\\infty$. A martingale that is stopped at a stopping time is still martingale and thus must have constant expectation. So:</p>\n<p>$1=Z(0)=\\mathbb{E}Z(t\\land\\tau_m)=\\mathbb{E}[\\exp{\\sigma W(t\\land\\tau_m)-\\frac{1}{2}\\sigma^2(t\\land\\tau_m)}]$ $t\\land\\tau_m$ means the minimum of $t$ and $\\tau_m$</p>\n<p>If $\\tau_m<\\infty$, the term $\\exp{-\\frac{1}{2}\\sigma^2(t\\land\\tau_m)}$ is equal to $\\exp{-\\frac{1}{2}\\sigma^2\\tau_m}$ for large enough $t$. $\\tau_m=\\infty$, the result converges to zero. So: </p>\n<p>$\\lim_{t\\to\\infty}\\exp{\\sigma W(t\\land\\tau_m)-\\frac{1}{2}\\sigma^2(t\\land\\tau_m)}=\\mathbb{I}_\\exp{\\sigma m-\\frac{1}{2}\\sigma^2\\tau_m\\}$</p>\n<p>now we can obtain:</p>\n<p>$1=\\mathbb{E}[\\mathbb{I}_\\exp{\\sigma m-\\frac{1}{2}\\sigma^2\\tau_m}]$</p>\n<p>$\\mathbb{E}[\\mathbb{I}_\\exp{-\\frac{1}{2}\\sigma^2\\tau_m}]=e^{-\\sigma m}$</p>\n<p>when $\\sigma\\to0$, we get $\\mathbb{P}{\\tau_m<\\infty}=1$</p>\n<p>$\\tau_m$ is finite almost surely, so we may drop the indicator to obtain:</p>\n<p>$\\mathbb{E}[\\exp{-\\frac{1}{2}\\sigma^2\\tau_m}]=e^{-\\sigma m}$</p>\n<p><strong>Theorem</strong> For $m\\in \\mathbb{R}$, the first passage time of Brownian motion to level $m$ is finite almost surely, and the Laplace transform of its distribution is given by </p>\n<p>$\\mathbb{E}e^{-\\alpha \\tau_m}=e^{-\\vert m \\vert\\sqrt{2\\alpha}}$ for all $\\alpha>0$</p>\n<p>differentiation: $\\mathbb{E}[\\tau_me^{-\\alpha\\tau_m}]=\\frac{\\vert m\\vert}{\\sqrt{2\\alpha}}e^{-\\vert m\\vert\\sqrt{2\\alpha}}$ for all $\\alpha>0$</p>\n<p>let $\\alpha\\to 0$ get obtain $\\mathbb{E}\\tau_m=\\infty$ so long as $m\\neq0$</p>\n<h2 id=\"Reflection-Principle\"><a href=\"#Reflection-Principle\" class=\"headerlink\" title=\"Reflection Principle\"></a>Reflection Principle</h2><h3 id=\"Reflection-Equality\"><a href=\"#Reflection-Equality\" class=\"headerlink\" title=\"Reflection Equality\"></a>Reflection Equality</h3><p>for each Brownian motion path that reaches level m prior to time t but is at a level w below m at time t, there is a “reflected path” that is at level $2m-w$ at time $t$. This reflected path is constructed by switching the up and down moves of the Brownian motion from time $\\tau_m$onward.</p>\n<p><strong>Reflection equality</strong></p>\n<p>$\\mathbb{P}{\\tau_m\\le t,W(t)\\le w}=\\mathbb{P}{W(t)\\ge 2m-w},w\\le m,m>0$</p>\n<h3 id=\"First-Passage-Time-Distribution-1\"><a href=\"#First-Passage-Time-Distribution-1\" class=\"headerlink\" title=\"First Passage Time Distribution\"></a>First Passage Time Distribution</h3><p><strong>Theorem</strong> For all $m\\neq0$, the random variable $\\tau_m$ has cumulative distribution function:</p>\n<p>$\\mathbb{P}{\\tau_m\\le t}=\\frac{2}{\\sqrt{2\\pi}}\\int_{\\frac{\\vert m\\vert}{\\sqrt{t}}}^\\infty e^{-\\frac{y^2}{2}}dy$</p>\n<p>$f_{\\tau_m}(t)=\\frac{d}{dt}\\mathbb{P}=\\frac{\\vert m\\vert}{t\\sqrt{2\\pi t}}e^{-\\frac{m^2}{2t}}$</p>\n<p>PROOF</p>\n<p>Use the reflection equality, we obtain</p>\n<p>$\\mathbb{P}{\\tau_m\\le t,W(t)\\le m}=\\mathbb{P}{W(t)\\ge m}$</p>\n<p>if $W(t)\\ge m$, then we are guaranteed that $\\tau_m\\le t$. </p>\n<p>$\\mathbb{P}{\\tau_m\\le t,W(t)\\ge m}=\\mathbb{P}{W(t)\\ge m}$</p>\n<p>so,$\\mathbb{P}{\\tau_m\\le t}=2\\mathbb{P}{W(t)\\ge m}=\\frac{2}{\\sqrt{2\\pi t}}\\int_{m}^\\infty e^{-\\frac{x^2}{2t}}dx=\\frac{2}{\\sqrt{2\\pi}}\\int_{\\frac{\\vert m\\vert}{\\sqrt{t}}}^\\infty e^{-\\frac{y^2}{2}}dy$</p>\n<h3 id=\"Distribution-of-Brownian-Motion-and-Its-Maximum\"><a href=\"#Distribution-of-Brownian-Motion-and-Its-Maximum\" class=\"headerlink\" title=\"Distribution of Brownian Motion and Its Maximum\"></a>Distribution of Brownian Motion and Its Maximum</h3><p>define the <strong>maximum to date</strong> for Brownian motion</p>\n<p>$M(t)=\\max_{0\\le s\\le t}W(s)$</p>\n<p>Use the reflection equality, we can obtain the joint distribution of $W(t)$<br> and $M(t)$</p>\n<p><strong>Theorem</strong> For $t>0$, the joint density of $(M(t),W(t))$ is</p>\n<p>$f_{M(t),W(t)}(m,w)=\\frac{2(2m-w)}{t\\sqrt{2\\pi t}}e^{-\\frac{(2m-w)^2}{2t}}$</p>\n<p>PROOF</p>\n<p>$\\mathbb{P}{M(t)\\ge m,W(t)\\le w}=\\int_m^\\infty\\int_{-\\infty}^wf_{M(t),W(t)}(x,y)dydx$</p>\n<p>$\\mathbb{P}{W(t)\\ge 2m-w}=\\frac{1}{\\sqrt{2\\pi t}}\\int_{2m-w}^\\infty e^{-\\frac{z^2}{2t}}dz$</p>\n<p>From the reflection equality, </p>\n<p>$\\frac{1}{\\sqrt{2\\pi t}}\\int_{2m-w}^\\infty e^{-\\frac{z^2}{2t}}dz= \\int_m^\\infty\\int_{-\\infty}^wf_{M(t),W(t)}(x,y)dydx$</p>\n<p>Differentiate with respect to $m$</p>\n<p>$-\\int_{-\\infty}^wf_{M(t),W(t)}(m,y)dy=-\\frac{2}{\\sqrt{2\\pi t}}e^{-\\frac{(2m-w)^2}{2t}}$</p>\n<p>With respect to $w$, then we obtain the distribution</p>\n<p><strong>Corollary</strong> </p>\n<p>The conditional distribution of $M(t)$ given $W(t)=w$ is $f_{M(t)\\vert W(t)}(m\\vert w)=\\frac{2(2m-w)}{t}e^{-\\frac{2m(m-w)}{t}}$</p>\n"},{"layout":"posts","title":"OLS","date":"2022-04-17T16:00:00.000Z","_content":"\n<head>\n <script src=\"https://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML\" type=\"text/javascript\"></script>\n <script type=\"text/x-mathjax-config\">\n MathJax.Hub.Config({\n tex2jax: {\n skipTags: ['script', 'noscript', 'style', 'textarea', 'pre'],\n inlineMath: [['$','$']]\n }\n });\n </script>\n</head>\n\n# 简单回归模型\n\n$y=\\beta_0+\\beta_1 x+u$\n\n$x$ 和$u$ 的相关性?\n\n关键假定是,$u$ 的平均值与$x$ 无关,即$\\mathbb{E}[u\\vert x]=\\mathbb{E}u$,称之为**均值独立**\n\n$\\mathbb{E}[u\\vert x]=\\mathbb{E}u=0$ 称之为零条件均值假定,等于$0$定义了截距\n\n$\\mathbb{E}[y\\vert x]=\\beta_0+\\beta_1x$ 总体回归函数\n\n## 普通最小二乘法的推导\n\n$$\n\\\\mathbb{E}[y-\\beta_1x-\\beta_0]=0\\\\\\\\\\mathbb{E}[x(y-\\beta_1x-\\beta_0)]=0\n$$\n\n利用零条件均值假定,以及矩估计,或者使残差平方和最小,即可获得OLS一阶条件\n\n$$\n\\begin{align*}\\sum y_i-\\hat{\\beta_0}-\\hat{\\beta_1}x_i=0\\\\\\\\\\sum x_i(y_i-\\hat{\\beta_0}-\\hat{\\beta_1}x_i)=0\\end{align*}\n$$\n\nOLS回归线/样本回归函数:$\\hat{y}=\\hat{\\beta_0}+\\hat{\\beta_1}x$,是总体回归函数的一个样本估计,总体回归函数始终是未知的。\n\n## 统计量的性质\n\n$\\sum \\hat{u}_i=0$, $\\sum x_i\\hat{u}_i=0$ 这其实就是一阶条件\n\n定义:\n\n总平方和SST,解释平方和SSE,残差平方和SSR\n\n$SST=\\sum(y_i-\\bar{y})^2$\n\n$SSE=\\sum (\\hat{y}_i-\\bar{y})^2$\n\n$SSR=\\sum \\hat{u}_i^2$\n\nSST=SSE+SSR\n\n拟合优度$R^2=SSE/SST$,是可解释的波动与总波动之比\n\n## OLS估计量的期望和方差\n\n### OLS的无偏性\n\n**SLR.1** 线性与参数\n\n**SLR.2** 随机抽样,实践过程中,并不是所有横截面样本都可以看成是随机抽样的结果\n\n$y_i=\\beta_0+\\beta_1x_i+u_i$,其中$u_i$是第$i$ 次观测的误差或干扰,与残差不同 \n\n**SLR.3** 解释变量的样本有波动\n\n$x$ 的样本结果不是完全相同的数值\n\n**SLR.4** 零条件均值\n\n**下面证明OLS的无偏性**\n\n$\\hat{\\beta}_1=\\frac{\\sum(x_i-\\bar{x})y_i}{\\sum(x_i-\\bar{x})^2}=\\frac{\\sum(x_i-\\bar{x})y_i}{SST_x}=\\frac{\\sum(x_i-\\bar{x})(\\beta_0+\\beta_1x_i+u_i)}{SST_x}=\\beta_1+\\frac{\\sum d_iu_i}{SST_x}$,其中$d_i=x_i-\\bar{x}$\n\n因此,$\\mathbb{E}\\hat{\\beta}_1=\\beta_1,\\mathbb{E}\\hat{\\beta}_0=\\beta_0$\n\n无偏性是抽样分布的性质,并不能确定从特定样本中得到的估计值\n\n时序分析中将会放松SLR.2\n\n**SLR.5** 同方差性\n\n$Var(u\\vert x)=\\sigma^2$\n\n$\\sigma^2=\\mathbb{E}[u^2\\vert x]$,即$\\sigma^2$是$u$的无条件方差,也经常被成为误差方差或干扰方差\n\n若$Var(u\\vert x)$取决于$x$,则误差项表现出异方差性\n\n**定理 OLS估计量的抽样方差**\n\n在SLR.1-SLR.5条件下,对于样本值:\n\n$Var(\\hat{\\beta}_1)=\\frac{\\sigma^2}{SST_x}$\n\n$Var(\\hat{\\beta}_0)=\\frac{\\sigma^2\\bar{x}}{SST_x}+\\frac{\\sigma^2}{n}$\n\n从$\\hat{\\beta}_1=\\beta_1+\\frac{\\sum d_iu_i}{SST_x}$出发,$Var(\\hat{\\beta}_1)=\\frac{\\sum d_i^2\\sigma^2}{SST_x^2}=\\sigma^2/SST_x$\n\n一个小结论:\n\n$\\sum x_i^2\\ge\\sum(x_i-\\bar{x})^2$\n\n**误差方差的估计**\n\n$\\hat{u}_i=u_i-(\\hat{\\beta}_0-\\beta_0)-(\\hat{\\beta}_1-\\beta_1)x_i$\n\n$\\sigma^2$的一个无偏“估计量”是$\\sum u_i^2/n$ 但$u_i$不可观测\n\nOLS有两个约束条件,因此:\n\n$\\hat{\\sigma}^2=SSR/(n-2)$ 是一个无偏估计,有时记为$s^2$\n\n$$\n0=\\bar{u}-(\\hat{\\beta}_0-\\beta_0)-(\\hat{\\beta}_1-\\beta_1)\\bar{x}\\\\\\\\\\sum\\hat{u}_i^2=\\sum(u_i-(\\hat{\\beta}_0-\\beta_0)-(\\hat{\\beta}_1-\\beta_1)x_i)^2\\\\\\\\=\\sum(u_i-\\bar{u}-(\\hat{\\beta}_1-\\beta_1)(x_i-\\bar{x}))^2\n$$\n\n$sd(\\hat{\\beta}_1)=\\sigma/\\sqrt{SST}$它的一个比较自然的估计量就是$se(\\hat{\\beta}_1)=\\hat{\\sigma}/\\sqrt{SST}$,被称之为标准误(standard error)\n\n# 多元回归分析:估计\n\n## 如何得到OLS估计值\n\n一阶条件:\n\n$$\n\\sum(y\\_i-\\hat{\\beta}\\_0-\\hat{\\beta}\\_1x\\_{i1}-\\cdots)=0\\\\\\\\\\sum x\\_{i1}(y\\_i-\\hat{\\beta}_0-\\hat{\\beta}\\_1x\\_{i1}-\\cdots)=0\\\\\\\\\\vdots\\\\\\\\\\sum x\\_{ik}(y\\_i-\\hat{\\beta}\\_0-\\hat{\\beta}\\_1x\\_{i1}-\\cdots)=0\n$$\n\n回归线或样本回归函数由截距估计值与斜率估计值组成\n\n估计值$\\hat{\\beta}_i$具有偏效应,因此多元回归使我们在对自变量的值不加限制的时候有效模拟施加限制的情况\n\n## 拟合值和残差的重要性质\n\n1. 残差样本平均值为零\n2. OLS拟合值和OLS残差之间的样本协方差为零\n3. 样本平均在回归线上\n\n考虑$\\hat{y}=\\hat{\\beta}\\_0+\\hat{\\beta}\\_1x_1+\\hat{\\beta}\\_2x\\_2$,$\\hat{\\beta}\\_1$的一种表达形式是:$\\hat{\\beta}\\_1=\\frac{\\sum\\hat{r}\\_{i1}y\\_i}{\\sum\\hat{r}\\_{i1}^2}$\n\n其中$\\hat{r}\\_{i1} $是$x\\_1$对$x\\_2$的回归得到的OLS残差,即$x_{i1}$与$x_{i2}$中不相关的部分,所以$\\hat{\\beta}\\_1$就是排除了$x\\_2$影响后$y$与$x\\_1$之间的关系\n\n### 简单回归与多元回归\n\n$\\tilde{y}=\\tilde{\\beta}_0+\\tilde{\\beta}_1x_1$和$\\hat{y}=\\hat{\\beta}_0+\\hat{\\beta}_1x_1+\\hat{\\beta}_2x_2$的结果会有什么关系?\n\n令$\\bar{\\delta}$是$x_2$对$x_1$的简单回归斜率,则$\\tilde{\\beta}_1=\\hat{\\beta}_1+\\hat{\\beta}_2\\bar{\\delta}$\n\n**拟合优度相关的内容和简单线性回归一致**\n\n增加一个自变量之后$R^2$不会减小,而且通常会增大\n\n## OLS估计量的期望\n\n**MLR.1** 线性于参数\n\n**MLR.2** 随机抽样\n\n**MLR.3** 不存在完全共线性\n\n**MLR.4** 条件均值为零\n\n当MLR.4成立时,我们说具有外生解释变量,如果$x_j$与$u$相关,那么$x_j$称之为内生解释变量\n\n限制了无法观测的因素与解释变量之间的关系\n\n在MLR1-4条件下,可以证明OLS的无偏性$\\mathbb{E}\\hat{\\beta}_i=\\beta_i$\n\n包含无关变量一般不会对OLS的无偏性产生影响,但是会对方差产生不利影响\n\n**遗漏变量偏误**\n\n总体模型:$y=\\beta_0+\\beta_1x_1+\\beta_2x_2+\\beta_3x_3+u$\n\n遗漏变量后的估计模型:$\\tilde{y}=\\tilde{\\beta}_0+\\tilde{\\beta}_1x_1+\\tilde{\\beta}_2x_2$\n\n**假设$x_2$和$x_3$无关,$x_1$和$x_3$相关**\n\n$$\n\\mathbb{E}\\tilde{\\beta}\\_1=\\beta\\_1+\\beta\\_3\\frac{\\sum x\\_{i3}(x\\_{i1}-\\bar{x}\\_1)}{\\sum (x\\_{i1}-\\bar{x}\\_1)^2}\n$$\n\n**MLR.5** 同方差性 $Var[u\\vert x_1,x_2,\\dots,x_k]=\\sigma^2$\n\n即以解释变量为条件,不管解释变量出现怎样的组合,误差项的方差都是一样的。如果不成立称之为异方差性\n\nMLR1-5称之为横截面回归的**高斯-马尔可夫**假定\n\n$Var\\hat{\\beta}_i=\\frac{\\sigma^2}{SST_j(1-R_j^2)}$,其中$R_j$来自于$x_j$对其他变量回归得到的$R^2$,需要MLR.5的的成立\n\n两个或多个自变量之间高度但不完全相关称之为**多重共线性**,即$R_j^2$接近于1,但这并不违反MLR.3,最终的问题还是要看$\\hat{\\beta}_j$与自身的标准差的大小关系\n\n很小的$SST_j$也可以导致大方差,即小样本容量会导致很大的抽样方差\n\n如果存在相关性的自变量和我们关注的自变量没有高度相关,其实没有直接影响,就不必关心这种共线性\n\n误设模型中的方差\n\n$Var\\hat{\\beta}_i=\\frac{\\sigma^2}{SST_j(1-R_j^2)}$,和$Var\\tilde{\\beta}_i=\\frac{\\sigma^2}{SST_j}$\n\n若$\\beta_2\\neq0$,则简单模型给出方差更小的有偏估计;若$\\beta_2=0$,则简单模型给出方差更小的无偏估计。\n\n直觉上讲,如果$x_2$对$y$没有偏效应,在回归中加入$x_2$只会加剧多重共线性。如果$\\beta_2\\neq0$,则偏误不会随着样本容量扩大而减小,但是Var会随着样本容量增大而趋于零,因此增加自变量导致的多重共线性就会变得没那么重要,大样本情况下倾向使用更复杂的模型\n\n### OLS估计的标准误\n\n$$\n\\hat{\\sigma}^2=\\frac{\\sum u_i^2}{n-k-1}=\\frac{SSR}{n-k-1}\n$$\n\n自由度$df=n-k-1$\n\n可以证明,$\\mathbb{E}\\hat{\\sigma}^2=\\sigma^2$\n\n$\\hat{\\sigma}=\\sqrt{\\hat{\\sigma}^2}$称之为回归标准误SER,是误差项的标准差的估计量,还被称之为估计值标准误和均方误差\n\n$se(\\hat{\\beta}_i)=\\frac{\\hat{\\sigma}^2}{\\sqrt{SST_j(1-R_j)^2}}$\n\n异方差性质不会导致参数估计偏误,但是会导致$Var(\\hat{\\beta}_j)$出现问题,导致标准误无效\n\n## OLS的有效性\n\n在MLR1-5的假定下,OKS估计量是最优线性无偏估计量BLUE,即具有最小的方差。尤其是MLR.5,保证了OLS在线性无偏估计量中具有最小的方差\n\n# 多元回归分析:推断\n\n## OLS估计量的抽样分布\n\n**MLR.6** 正态性 总体误差$u$独立于解释变量,并且服从均值为零,方差为$\\sigma^2$的正态分布\n\nMLR1-6称之为经典线性模型(CLM)假定。在CLM下,OLS是最小方差的无偏估计,不必限制在线性估计中\n\n由千于$u$ 是影响着 $y$ 而又观测不到的许多因素之和,所以我们可借助中心极限定理断定 $u$ 具有近似正态分布\n\n通常我们可以利用某种变换得到一个$u$接近于正态的分布\n\n误差项的正态性导致了OLS估计量的正态抽样分布\n\n$$\n\\frac{\\hat{\\beta}_j-\\beta_j}{sd(\\hat{\\beta}_j)}\\sim Normal(0,1)\n$$\n\n## 对单个总体参数的检验:t检验\n\n在CLM假定下,$\\frac{\\hat{\\beta}\\_j-\\beta\\_j}{se(\\hat{\\beta}\\_j)}\\sim t\\_{n-k-1}$\n\n多数应用中,主要兴趣在于检验原假设$H_0:\\beta_j=0$\n\n为什么不反过来写?因为$x_j$对$y$有偏效应的表述对$\\beta_j$不为零对任何一个值都成立\n\n$t_{\\hat{\\beta}_j}=\\hat{\\beta}_j/se(\\hat{\\beta}_j)$称之为t统计量\n\n**单侧/双侧备择假设,t检验p值 ,置信区间**\n\n参考概统知识,此处不表\n\n## 检验关于参数的一个线性组合假设\n\n$H_0:\\beta_1=\\beta_2$ 如何检验?\n\n$t=\\frac{\\hat{\\beta}_1-\\hat{\\beta}_2}{se(\\hat{\\beta}_1-\\hat{\\beta}_2)}$,关键是求解标准误,即要求解$Cov(\\hat{\\beta}_1,\\hat{\\beta}_2)$的一个估计值,这在数学上是复杂的\n\n但我们可以改写模型$\\beta_1=\\theta_1+\\beta_2$\n\n$y=\\beta_0+(\\theta_1+\\beta_2)x_1+\\beta_2x_2+u=\\beta_0+\\theta_1x_1+\\beta_2(x_1+x_2)+u$\n\n直接检验$\\theta_1$即可\n\n## 对多个线性约束对检验:F检验\n\n原假设:$H_0:\\beta_{k-q+1}=0,\\dots\\beta_k=0$\n\n不含$\\beta_{\\dots}$的模型是受约束模型,原始模型称之为不受约束模型\n\n受约束模型增加了$q$个排除性约束,定义$F$统计量\n\n$$\nF=\\frac{(SSR_r-SSR_{ur})/q}{SSR_{ur}/(n-k-1)}=\\frac{(R_{ur}^2-R_r^2)/q}{(1-R_{ur}^2)/df_{ur}}\\sim F_{q,n-k-1}\n$$\n\n其中$SSR_r$是受约束模型的残差平方和,$SSR_{ur}$是不受约束的残差平方和,$q=df_r-df_{ur}$\n\n如果拒绝原假设,那么就说$x_{k-q+1},\\dots x_k$ 在适当的显著性水平上是联合统计显著的\n\n**对于一般的线性约束**\n\n如指定了$\\beta_1=1$,则将$x_1$挪到回归方程左边\n\n由于两次的因变量不同,不能采用$R^2$形式的统计量\n\n# 多元回归分析:OLS的渐进性\n\n## 一致性\n\n直观的理解:当样本量趋于无穷时,收敛到真值\n\n**Theory OLS**的一致性\n\n在MLR1-4下,$\\hat{\\beta}_j$是$\\hat{\\beta}_j$的一致估计\n\n*PROOF*\n\n$$\nX\\beta+u=y\\\\\\\\\\hat{\\beta}=(X^TX)^{-1}X^Ty=(X^TX)^{-1}X^T(X\\beta+u)\\\\\\\\=\\beta+(X^TX)^{-1}X^Tu=\\beta+(\\frac{1}{n}\\sum_{i=1}^n x_i^Tx_i)^{-1}(\\frac{1}{n}\\sum _{i=1}^nx_i^Tu)\n$$\n\naccording to the large number law:\n\n$$\n\\frac{1}{n}\\sum x_i^Tx_i\\xrightarrow{p}\\mathbb{E}x_i^Tx_i=A,\\quad \\frac{1}{n}\\sum x_i^T u\\xrightarrow{p}\\mathbb{E}x_iu=0\n$$\n\nbecause $A$ is a nonsingular matrix, so$(\\frac{1}{n}\\sum x_i^Tx_i)^{-1}\\xrightarrow{p}A^{-1}$\n\n$$\nplim \\hat{\\beta}=\\beta+A^{-1}\\cdot0=\\beta\n$$\n\n**假设MLR.4’ 零均值和零相关**\n\n对所有的$j$,都有$\\mathbb{E}u=0$和$Cov(x_j,u)=0$\n\n这是一个比MLR.4更弱的假定,它只要求每个$x_j$与$u$无关。\n\n这导致$x_j$的非线性函数可能与误差相关\n\n**OLS的不一致性**\n\n如果误差与任何一个自变量相关,那么OLS就是有偏而不一致的估计。随着样本容量的增大,偏误将持续存在。\n\n$$\nplim \\hat{\\beta_1}-\\beta_1=\\frac{Cov(x_1,u)}{Var(x_1)}\n$$\n\n不一致性用总体的性质表示,而偏误则基于样本的对应量表示\n\n## 渐近正态和大样本推断\n\n**Theory** OLS的渐进正态性\n\n在MLR1-5下,\n\n1. \n$\\sqrt{n}(\\hat{\\beta}\\_j-\\beta\\_j)\\xrightarrow x N(0,\\sigma^2/a\\_j^2),a\\_j^2=plim(n^{-1}\\sum_{i=1}^n \\hat{r\\_{ij}}^2)$,其中$\\hat{r}\\_{ij}$是$x\\_j$对其余自变量回归得到的残差,即不能被其他变量解释的部分,我们称$\\hat{\\beta}\\_j$是渐进正态分布的\n2. $\\hat{\\sigma}^2$是$\\sigma^2=Var(u)$的一个一致估计\n3. 对于每个$j$都有$(\\hat{\\beta}_j-\\beta_j)/sd(\\hat{\\beta}_j)\\xrightarrow x N(0,1)$,且$(\\hat{\\beta}_j-\\beta_j)/se(\\hat{\\beta}_j)\\xrightarrow x N(0,1)$\n\n去掉了MLR.6,只需要有限方差且零均值与同方差性质\n\n总体分布恒定,与样本数量大小没有关系\n\n$\\hat{\\beta}_j$的估计方差:$\\hat{Var(\\hat{\\beta}_j)}=\\frac{\\hat{\\sigma}^2}{SST_j(1-R_j^2)}$,以$1/n$的速度收缩至零\n\n### 拉格朗日乘数LM统计量\n\n1. 将$y$对施加限制后的自变量集回归,保存残差$\\tilde{u}$\n2. 将$\\tilde{u}$对所有自变量进行回归,得到$R_u^2$\n3. 计算$LM=nR_u^2$\n4. 将LM与$\\chi_q^2$分布中适当的临界值$c$比较,如果$LM>c$,则拒绝原假设,说明后$q$个变量的系数不为零\n\n## OLS的渐近有效性\n\n在模型$y=\\beta_0+\\beta_1x_1+u$中,在MLR.4假设下,$\\mathbb{E}[u\\vert x]=0$,我们关注斜率\n\n令$z_i=g(x_i)$,$g$为任意函数,那么$u$就与$g(x)$无关。假定$Cov(z,x)\\neq 0$,那么,估计量\n\n$$\n\\tilde{\\beta}_1=\\sum(z_i-\\bar{z})y_i/\\sum (z_i-\\bar{z})x_i\n$$\n\n是对$\\beta_1$的一致估计。(证明:在分子分母分别除n并使用大数定律)\n\n$$\nplim \\tilde{\\beta_1}=\\beta_1+Cov(z,u)/Cov(z,x)=\\beta_1\n$$\n\n**Theory** OlS的渐近有效性\n\n高斯-马尔可夫假设下,OLS估计量具有最小的渐近方差,\n\n$$\nAvar \\sqrt{n}(\\hat{\\beta}_j-\\beta_j)\\le Avar\\sqrt{n}(\\tilde{\\beta}_j-\\beta_j)\n$$\n\n# 深入专题\n\n## 数据测度单位对 OLS 统计量的影晌\n\n度量单位对系数、标准误、置信区间、t统计量、F统计量的影响不会影响结果。\n\n**$\\beta$系数**\n\n将所有变量都标准化后的回归结果得到的系数称为标准化系数或$\\beta$系数 $\\hat{b}_j=(\\delta_j/\\delta_y)\\hat{\\beta}_j$\n\n由此得到的$\\beta$系数大小更具有说服力\n\n## 函数形式的进一步讨论\n\n### 对数函数\n\n$\\log(y)=\\hat{\\beta}_0+\\hat{\\beta}_1\\log x_1+\\hat{\\beta}_2x_2$\n\n固定$x_1$不变,有$\\Delta \\hat{\\log y}=\\hat{\\beta}_2 \\Delta x_2$,即$\\%\\Delta\\hat{y}=100\\cdot[\\exp(\\hat{\\beta}_2\\Delta x_2)-1]$是精确的预测变化百分比,它是一致的,但却不是无偏的,因为指数函数的非线性\n\n**对数的好处:**\n\n1. 斜率系数不随测度单位而变化,所以我们可以忽略以对数形式出现的变量的度量单位\n2. 严格为正的变量,条件分布常常具有异方差性或偏态性,取对数后可以降低\n3. 对数通常可以缩小变量的取值范围,对极端值也没有那么敏感\n\n**问题:**\n\n1. 变量在0、1之间时,会导致变换后的数据绝对值很大\n2. 更加难以预测原变量的值。两者的$R^2$也不具有可比性\n\n### 含二次式的模型\n\n一次项导致的变化表达式要重写,和变量本身也有关\n\n### 含有交互项的模型\n\n$y=\\beta_0+\\beta_1x_1+\\beta_2x_2+\\beta_3x_1x_2+u$$y=\\beta_0+\\beta_1x_1+\\beta_2x_2+\\beta_2x_1x_2+u$\n\n此时$\\beta_2$是$x_1=0$时$x_2$对$y$的偏效应,没什么意义\n\n$y=\\beta_0+\\beta_1x_1+\\beta_2x_2+\\beta_3(x_1-\\mu_1)(x_2-\\mu_2)+u$\n\n这样就是在均值处的偏效应了\n\n## 拟合优度和回归元选择的进一步探讨\n\n较小的$R^2$意味着误差方差相对$y$的方差太大了,以及我们很难精确地估计$\\beta_j$,但大样本容量可以抵消较大的误差方差。\n\n### 调整$R^2$\n\n$R^2=1-\\frac{SSR/n}{SST/n}$\n\n总体$R^2$定义为$1-\\sigma_u^2/\\sigma_y^2$,这是$y$的变化在总体中可以用自变量解释的部分比例,是我们希望用$R^2$估计的值\n\n但是用$SSR/n$估计$\\sigma_u^2$是有偏的,用$\\hat{\\sigma}^2=SSR/(n-k-1)$显然更好,同理,用$SST/(n-1)$代替$SST/n$\n\n由此,得到调整$R^2$:\n\n$\\bar{R^2}=1-\\hat{\\sigma}^2/[SST/(n-1)]=1-(1-R^2)\\frac{n-1}{n-k-1}$\n\n虽然两个无偏估计的比不是无偏估计,但是$\\bar{R^2}$在模型中额外增加自变量时施加了惩罚,在回归中增加一个变量时,只有新变量的t统计量大于1,$\\bar{R^2}$才会提高,增加一组变量时,联合检验显著的F统计量大于1才会提高\n\n### 利用调整$R^2$在两个非嵌套模型 (nonnested) 中进行选择\n\nDefinition: 两个方程没有哪一个是另一个的特殊情形,所以它们是非嵌套模型\n\n在这种情况下,使用普通$R^2$对自变量较少的模型不公平\n\n当自变量组对应着不同的函数形式时,调整$R^2$也是有价值的\n\n遗憾的是,**不能**通过拟合优度决定不同的因变量形式,因为它们的总变化是不同的,拟合的是两个完全不同的因变量\n\n**回归分析中控制过多的因素**\n\n注重对回归做其他条件不变的解释即可\n\n**增加回归元以减少误差方差**\n\n增加适当的无关变量可以减小误差方差,在大样本容量的情况下,所有OLS估计量对标准误都会减小\n\n## 预测和残差分析\n\n### 预测的置信区间\n\n估计方程:$\\hat{y}=\\hat{\\beta}_0+\\hat{\\beta}_1x_1+\\hat{\\beta}_2x_2+\\dots$\n\n$\\theta_0=\\beta_0+\\beta_1c_1+\\beta_2c_2+\\dots$ 的估计量是:\n\n$\\hat{\\theta}_0=\\hat{\\beta}_0+\\hat{\\beta}_1c_1+\\hat{\\beta}_2c_2+\\dots$ 我们关注它的置信区间\n\n在$df$较大的情况下,我们可以利用经验法则$\\hat{\\theta}_0\\pm2\\cdot se(\\hat{\\theta}_0)$构造95%置信区间\n\n求$se(\\hat{\\theta}_0)$:\n\n$\\theta_0$表达式代入方程:$y=\\theta_0+\\beta_1(x_1-c_1)+\\beta_2(x_2-c_2)+\\dots$\n\n用样本回归一下就可以了,截距项是预测值,还可以得到标准误\n\n由于每个解释变量的样本均值都为零时,截距估计量的方差最小,所以当$x_j$都取均值时,预测值的方差最小。随着$c_j$的值离中心越来越远,误差越来越大\n\n令$y^0$表示我们构造一个置信区间(预测区间)的估计值\n\n$$\n\\hat{y}^0=\\hat{\\beta}_0+\\hat{\\beta}_1x_1^0+\\cdots+\\\\\\\\\\hat{e}^0=y^0-\\hat{y}^0=\\beta_0+\\beta_1x_1^0+\\cdots+u^0-\\hat{y}^0\\\\\\\\\\mathbb{E}\\hat{e}^0=0\n$$\n\n所以预测误差的期望值为零\n\n$u^0$与用来得到$\\hat{\\beta}_j$的样本方差不相关,$u^0$与每个$\\hat{\\beta}_j$都不相关,所以$u^0$与$\\hat{y}^0$不相关\n\n$$\nVar(\\hat{e}^0)=Var(\\hat{y}^0)+Var(u^0)=Var(\\hat{y}^0)+\\sigma^2\n$$\n\n第一项来自抽样误差,即对$\\beta_j$的估计误差\n\n$se(\\hat{e}^0)=\\sqrt{se(\\hat{y}^0)^2+\\hat{\\sigma}^2}$\n\n### 残差分析\n\n计算剔除某些因素后样本的水平\n\n### 因变量为$\\log y$时对$y$的预测\n\n$\\hat{y}=\\exp(\\hat{\\log y})?$ 会系统地**低估**$y$的预测值\n\n$\\mathbb{E}[y\\vert x]=\\exp(\\sigma^2/2)\\cdot \\exp(\\beta_0+\\beta_1x_1+\\beta_2x_2+\\dots)$\n\n$\\hat{y}=\\exp(\\hat{\\sigma}^2/2)\\exp(\\hat{\\log y})$,虽然不是无偏的,但是是一致的。它依赖于$u$的正态性\n\n一般的情况,$\\mathbb{E}[y\\vert x]=\\alpha_0\\cdot \\exp(\\beta_0+\\beta_1x_1+\\beta_2x_2+\\dots)$,$\\alpha_0$是$\\exp(u)$的期望值,且是大于一的,所以我们要求$\\hat{\\alpha}_0$\n\n矩估计$\\hat{\\alpha}\\_0=\\frac{1}{n}\\sum\\exp(\\hat{u}\\_i)$,是一个一致有偏的估计量,这是所谓的污染估计值的一种特殊形式。或者我们可以通过一个过原点的简单回归:$m\\_i=\\exp(\\beta\\_0+\\beta\\_1x\\_{i1}+\\beta\\_2x\\_{i2}+\\dots),\\mathbb{E}[y\\_i\\vert m\\_i]=\\alpha\\_0m\\_i$,这样,我们就能从$y_i$对$\\hat{m}_i$的回归中得到一个$\\alpha_0$的无偏估计:\n\n$$\n\\tilde{\\alpha}_0=\\frac{\\sum\\hat{m}_iy_i}{\\sum\\hat{m}_i^2}\n$$\n\n**拟合优度**\n\n在普通最小二乘中,$R^2$就是$\\hat{y}_i$与$y_i$之间的相关系数的平方,如果我们对所有观测量都计算$\\hat{y}_i=\\hat{\\alpha}_0m_i$,由于是在变量上乘了一个常数$\\hat{\\alpha}_0$,所以对$\\alpha_0$的估计不会影响到结果。我们还是计算$y\n_i$和$\\hat{y}\n_i$的相关系数,这样就可以在不同的因变量模型之间对比拟合优度\n\n# 含有定性信息的多元回归分析: 二值(或虚拟)变量\n\n本部分在劳动经济学中较多涉及,不再赘述","source":"_posts/OLS method.md","raw":"---\nlayout: posts\ntitle: OLS \ndate: 2022-04-18\ncategories: 学习笔记\ntags: [经济,]\n\n---\n\n<head>\n <script src=\"https://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML\" type=\"text/javascript\"></script>\n <script type=\"text/x-mathjax-config\">\n MathJax.Hub.Config({\n tex2jax: {\n skipTags: ['script', 'noscript', 'style', 'textarea', 'pre'],\n inlineMath: [['$','$']]\n }\n });\n </script>\n</head>\n\n# 简单回归模型\n\n$y=\\beta_0+\\beta_1 x+u$\n\n$x$ 和$u$ 的相关性?\n\n关键假定是,$u$ 的平均值与$x$ 无关,即$\\mathbb{E}[u\\vert x]=\\mathbb{E}u$,称之为**均值独立**\n\n$\\mathbb{E}[u\\vert x]=\\mathbb{E}u=0$ 称之为零条件均值假定,等于$0$定义了截距\n\n$\\mathbb{E}[y\\vert x]=\\beta_0+\\beta_1x$ 总体回归函数\n\n## 普通最小二乘法的推导\n\n$$\n\\\\mathbb{E}[y-\\beta_1x-\\beta_0]=0\\\\\\\\\\mathbb{E}[x(y-\\beta_1x-\\beta_0)]=0\n$$\n\n利用零条件均值假定,以及矩估计,或者使残差平方和最小,即可获得OLS一阶条件\n\n$$\n\\begin{align*}\\sum y_i-\\hat{\\beta_0}-\\hat{\\beta_1}x_i=0\\\\\\\\\\sum x_i(y_i-\\hat{\\beta_0}-\\hat{\\beta_1}x_i)=0\\end{align*}\n$$\n\nOLS回归线/样本回归函数:$\\hat{y}=\\hat{\\beta_0}+\\hat{\\beta_1}x$,是总体回归函数的一个样本估计,总体回归函数始终是未知的。\n\n## 统计量的性质\n\n$\\sum \\hat{u}_i=0$, $\\sum x_i\\hat{u}_i=0$ 这其实就是一阶条件\n\n定义:\n\n总平方和SST,解释平方和SSE,残差平方和SSR\n\n$SST=\\sum(y_i-\\bar{y})^2$\n\n$SSE=\\sum (\\hat{y}_i-\\bar{y})^2$\n\n$SSR=\\sum \\hat{u}_i^2$\n\nSST=SSE+SSR\n\n拟合优度$R^2=SSE/SST$,是可解释的波动与总波动之比\n\n## OLS估计量的期望和方差\n\n### OLS的无偏性\n\n**SLR.1** 线性与参数\n\n**SLR.2** 随机抽样,实践过程中,并不是所有横截面样本都可以看成是随机抽样的结果\n\n$y_i=\\beta_0+\\beta_1x_i+u_i$,其中$u_i$是第$i$ 次观测的误差或干扰,与残差不同 \n\n**SLR.3** 解释变量的样本有波动\n\n$x$ 的样本结果不是完全相同的数值\n\n**SLR.4** 零条件均值\n\n**下面证明OLS的无偏性**\n\n$\\hat{\\beta}_1=\\frac{\\sum(x_i-\\bar{x})y_i}{\\sum(x_i-\\bar{x})^2}=\\frac{\\sum(x_i-\\bar{x})y_i}{SST_x}=\\frac{\\sum(x_i-\\bar{x})(\\beta_0+\\beta_1x_i+u_i)}{SST_x}=\\beta_1+\\frac{\\sum d_iu_i}{SST_x}$,其中$d_i=x_i-\\bar{x}$\n\n因此,$\\mathbb{E}\\hat{\\beta}_1=\\beta_1,\\mathbb{E}\\hat{\\beta}_0=\\beta_0$\n\n无偏性是抽样分布的性质,并不能确定从特定样本中得到的估计值\n\n时序分析中将会放松SLR.2\n\n**SLR.5** 同方差性\n\n$Var(u\\vert x)=\\sigma^2$\n\n$\\sigma^2=\\mathbb{E}[u^2\\vert x]$,即$\\sigma^2$是$u$的无条件方差,也经常被成为误差方差或干扰方差\n\n若$Var(u\\vert x)$取决于$x$,则误差项表现出异方差性\n\n**定理 OLS估计量的抽样方差**\n\n在SLR.1-SLR.5条件下,对于样本值:\n\n$Var(\\hat{\\beta}_1)=\\frac{\\sigma^2}{SST_x}$\n\n$Var(\\hat{\\beta}_0)=\\frac{\\sigma^2\\bar{x}}{SST_x}+\\frac{\\sigma^2}{n}$\n\n从$\\hat{\\beta}_1=\\beta_1+\\frac{\\sum d_iu_i}{SST_x}$出发,$Var(\\hat{\\beta}_1)=\\frac{\\sum d_i^2\\sigma^2}{SST_x^2}=\\sigma^2/SST_x$\n\n一个小结论:\n\n$\\sum x_i^2\\ge\\sum(x_i-\\bar{x})^2$\n\n**误差方差的估计**\n\n$\\hat{u}_i=u_i-(\\hat{\\beta}_0-\\beta_0)-(\\hat{\\beta}_1-\\beta_1)x_i$\n\n$\\sigma^2$的一个无偏“估计量”是$\\sum u_i^2/n$ 但$u_i$不可观测\n\nOLS有两个约束条件,因此:\n\n$\\hat{\\sigma}^2=SSR/(n-2)$ 是一个无偏估计,有时记为$s^2$\n\n$$\n0=\\bar{u}-(\\hat{\\beta}_0-\\beta_0)-(\\hat{\\beta}_1-\\beta_1)\\bar{x}\\\\\\\\\\sum\\hat{u}_i^2=\\sum(u_i-(\\hat{\\beta}_0-\\beta_0)-(\\hat{\\beta}_1-\\beta_1)x_i)^2\\\\\\\\=\\sum(u_i-\\bar{u}-(\\hat{\\beta}_1-\\beta_1)(x_i-\\bar{x}))^2\n$$\n\n$sd(\\hat{\\beta}_1)=\\sigma/\\sqrt{SST}$它的一个比较自然的估计量就是$se(\\hat{\\beta}_1)=\\hat{\\sigma}/\\sqrt{SST}$,被称之为标准误(standard error)\n\n# 多元回归分析:估计\n\n## 如何得到OLS估计值\n\n一阶条件:\n\n$$\n\\sum(y\\_i-\\hat{\\beta}\\_0-\\hat{\\beta}\\_1x\\_{i1}-\\cdots)=0\\\\\\\\\\sum x\\_{i1}(y\\_i-\\hat{\\beta}_0-\\hat{\\beta}\\_1x\\_{i1}-\\cdots)=0\\\\\\\\\\vdots\\\\\\\\\\sum x\\_{ik}(y\\_i-\\hat{\\beta}\\_0-\\hat{\\beta}\\_1x\\_{i1}-\\cdots)=0\n$$\n\n回归线或样本回归函数由截距估计值与斜率估计值组成\n\n估计值$\\hat{\\beta}_i$具有偏效应,因此多元回归使我们在对自变量的值不加限制的时候有效模拟施加限制的情况\n\n## 拟合值和残差的重要性质\n\n1. 残差样本平均值为零\n2. OLS拟合值和OLS残差之间的样本协方差为零\n3. 样本平均在回归线上\n\n考虑$\\hat{y}=\\hat{\\beta}\\_0+\\hat{\\beta}\\_1x_1+\\hat{\\beta}\\_2x\\_2$,$\\hat{\\beta}\\_1$的一种表达形式是:$\\hat{\\beta}\\_1=\\frac{\\sum\\hat{r}\\_{i1}y\\_i}{\\sum\\hat{r}\\_{i1}^2}$\n\n其中$\\hat{r}\\_{i1} $是$x\\_1$对$x\\_2$的回归得到的OLS残差,即$x_{i1}$与$x_{i2}$中不相关的部分,所以$\\hat{\\beta}\\_1$就是排除了$x\\_2$影响后$y$与$x\\_1$之间的关系\n\n### 简单回归与多元回归\n\n$\\tilde{y}=\\tilde{\\beta}_0+\\tilde{\\beta}_1x_1$和$\\hat{y}=\\hat{\\beta}_0+\\hat{\\beta}_1x_1+\\hat{\\beta}_2x_2$的结果会有什么关系?\n\n令$\\bar{\\delta}$是$x_2$对$x_1$的简单回归斜率,则$\\tilde{\\beta}_1=\\hat{\\beta}_1+\\hat{\\beta}_2\\bar{\\delta}$\n\n**拟合优度相关的内容和简单线性回归一致**\n\n增加一个自变量之后$R^2$不会减小,而且通常会增大\n\n## OLS估计量的期望\n\n**MLR.1** 线性于参数\n\n**MLR.2** 随机抽样\n\n**MLR.3** 不存在完全共线性\n\n**MLR.4** 条件均值为零\n\n当MLR.4成立时,我们说具有外生解释变量,如果$x_j$与$u$相关,那么$x_j$称之为内生解释变量\n\n限制了无法观测的因素与解释变量之间的关系\n\n在MLR1-4条件下,可以证明OLS的无偏性$\\mathbb{E}\\hat{\\beta}_i=\\beta_i$\n\n包含无关变量一般不会对OLS的无偏性产生影响,但是会对方差产生不利影响\n\n**遗漏变量偏误**\n\n总体模型:$y=\\beta_0+\\beta_1x_1+\\beta_2x_2+\\beta_3x_3+u$\n\n遗漏变量后的估计模型:$\\tilde{y}=\\tilde{\\beta}_0+\\tilde{\\beta}_1x_1+\\tilde{\\beta}_2x_2$\n\n**假设$x_2$和$x_3$无关,$x_1$和$x_3$相关**\n\n$$\n\\mathbb{E}\\tilde{\\beta}\\_1=\\beta\\_1+\\beta\\_3\\frac{\\sum x\\_{i3}(x\\_{i1}-\\bar{x}\\_1)}{\\sum (x\\_{i1}-\\bar{x}\\_1)^2}\n$$\n\n**MLR.5** 同方差性 $Var[u\\vert x_1,x_2,\\dots,x_k]=\\sigma^2$\n\n即以解释变量为条件,不管解释变量出现怎样的组合,误差项的方差都是一样的。如果不成立称之为异方差性\n\nMLR1-5称之为横截面回归的**高斯-马尔可夫**假定\n\n$Var\\hat{\\beta}_i=\\frac{\\sigma^2}{SST_j(1-R_j^2)}$,其中$R_j$来自于$x_j$对其他变量回归得到的$R^2$,需要MLR.5的的成立\n\n两个或多个自变量之间高度但不完全相关称之为**多重共线性**,即$R_j^2$接近于1,但这并不违反MLR.3,最终的问题还是要看$\\hat{\\beta}_j$与自身的标准差的大小关系\n\n很小的$SST_j$也可以导致大方差,即小样本容量会导致很大的抽样方差\n\n如果存在相关性的自变量和我们关注的自变量没有高度相关,其实没有直接影响,就不必关心这种共线性\n\n误设模型中的方差\n\n$Var\\hat{\\beta}_i=\\frac{\\sigma^2}{SST_j(1-R_j^2)}$,和$Var\\tilde{\\beta}_i=\\frac{\\sigma^2}{SST_j}$\n\n若$\\beta_2\\neq0$,则简单模型给出方差更小的有偏估计;若$\\beta_2=0$,则简单模型给出方差更小的无偏估计。\n\n直觉上讲,如果$x_2$对$y$没有偏效应,在回归中加入$x_2$只会加剧多重共线性。如果$\\beta_2\\neq0$,则偏误不会随着样本容量扩大而减小,但是Var会随着样本容量增大而趋于零,因此增加自变量导致的多重共线性就会变得没那么重要,大样本情况下倾向使用更复杂的模型\n\n### OLS估计的标准误\n\n$$\n\\hat{\\sigma}^2=\\frac{\\sum u_i^2}{n-k-1}=\\frac{SSR}{n-k-1}\n$$\n\n自由度$df=n-k-1$\n\n可以证明,$\\mathbb{E}\\hat{\\sigma}^2=\\sigma^2$\n\n$\\hat{\\sigma}=\\sqrt{\\hat{\\sigma}^2}$称之为回归标准误SER,是误差项的标准差的估计量,还被称之为估计值标准误和均方误差\n\n$se(\\hat{\\beta}_i)=\\frac{\\hat{\\sigma}^2}{\\sqrt{SST_j(1-R_j)^2}}$\n\n异方差性质不会导致参数估计偏误,但是会导致$Var(\\hat{\\beta}_j)$出现问题,导致标准误无效\n\n## OLS的有效性\n\n在MLR1-5的假定下,OKS估计量是最优线性无偏估计量BLUE,即具有最小的方差。尤其是MLR.5,保证了OLS在线性无偏估计量中具有最小的方差\n\n# 多元回归分析:推断\n\n## OLS估计量的抽样分布\n\n**MLR.6** 正态性 总体误差$u$独立于解释变量,并且服从均值为零,方差为$\\sigma^2$的正态分布\n\nMLR1-6称之为经典线性模型(CLM)假定。在CLM下,OLS是最小方差的无偏估计,不必限制在线性估计中\n\n由千于$u$ 是影响着 $y$ 而又观测不到的许多因素之和,所以我们可借助中心极限定理断定 $u$ 具有近似正态分布\n\n通常我们可以利用某种变换得到一个$u$接近于正态的分布\n\n误差项的正态性导致了OLS估计量的正态抽样分布\n\n$$\n\\frac{\\hat{\\beta}_j-\\beta_j}{sd(\\hat{\\beta}_j)}\\sim Normal(0,1)\n$$\n\n## 对单个总体参数的检验:t检验\n\n在CLM假定下,$\\frac{\\hat{\\beta}\\_j-\\beta\\_j}{se(\\hat{\\beta}\\_j)}\\sim t\\_{n-k-1}$\n\n多数应用中,主要兴趣在于检验原假设$H_0:\\beta_j=0$\n\n为什么不反过来写?因为$x_j$对$y$有偏效应的表述对$\\beta_j$不为零对任何一个值都成立\n\n$t_{\\hat{\\beta}_j}=\\hat{\\beta}_j/se(\\hat{\\beta}_j)$称之为t统计量\n\n**单侧/双侧备择假设,t检验p值 ,置信区间**\n\n参考概统知识,此处不表\n\n## 检验关于参数的一个线性组合假设\n\n$H_0:\\beta_1=\\beta_2$ 如何检验?\n\n$t=\\frac{\\hat{\\beta}_1-\\hat{\\beta}_2}{se(\\hat{\\beta}_1-\\hat{\\beta}_2)}$,关键是求解标准误,即要求解$Cov(\\hat{\\beta}_1,\\hat{\\beta}_2)$的一个估计值,这在数学上是复杂的\n\n但我们可以改写模型$\\beta_1=\\theta_1+\\beta_2$\n\n$y=\\beta_0+(\\theta_1+\\beta_2)x_1+\\beta_2x_2+u=\\beta_0+\\theta_1x_1+\\beta_2(x_1+x_2)+u$\n\n直接检验$\\theta_1$即可\n\n## 对多个线性约束对检验:F检验\n\n原假设:$H_0:\\beta_{k-q+1}=0,\\dots\\beta_k=0$\n\n不含$\\beta_{\\dots}$的模型是受约束模型,原始模型称之为不受约束模型\n\n受约束模型增加了$q$个排除性约束,定义$F$统计量\n\n$$\nF=\\frac{(SSR_r-SSR_{ur})/q}{SSR_{ur}/(n-k-1)}=\\frac{(R_{ur}^2-R_r^2)/q}{(1-R_{ur}^2)/df_{ur}}\\sim F_{q,n-k-1}\n$$\n\n其中$SSR_r$是受约束模型的残差平方和,$SSR_{ur}$是不受约束的残差平方和,$q=df_r-df_{ur}$\n\n如果拒绝原假设,那么就说$x_{k-q+1},\\dots x_k$ 在适当的显著性水平上是联合统计显著的\n\n**对于一般的线性约束**\n\n如指定了$\\beta_1=1$,则将$x_1$挪到回归方程左边\n\n由于两次的因变量不同,不能采用$R^2$形式的统计量\n\n# 多元回归分析:OLS的渐进性\n\n## 一致性\n\n直观的理解:当样本量趋于无穷时,收敛到真值\n\n**Theory OLS**的一致性\n\n在MLR1-4下,$\\hat{\\beta}_j$是$\\hat{\\beta}_j$的一致估计\n\n*PROOF*\n\n$$\nX\\beta+u=y\\\\\\\\\\hat{\\beta}=(X^TX)^{-1}X^Ty=(X^TX)^{-1}X^T(X\\beta+u)\\\\\\\\=\\beta+(X^TX)^{-1}X^Tu=\\beta+(\\frac{1}{n}\\sum_{i=1}^n x_i^Tx_i)^{-1}(\\frac{1}{n}\\sum _{i=1}^nx_i^Tu)\n$$\n\naccording to the large number law:\n\n$$\n\\frac{1}{n}\\sum x_i^Tx_i\\xrightarrow{p}\\mathbb{E}x_i^Tx_i=A,\\quad \\frac{1}{n}\\sum x_i^T u\\xrightarrow{p}\\mathbb{E}x_iu=0\n$$\n\nbecause $A$ is a nonsingular matrix, so$(\\frac{1}{n}\\sum x_i^Tx_i)^{-1}\\xrightarrow{p}A^{-1}$\n\n$$\nplim \\hat{\\beta}=\\beta+A^{-1}\\cdot0=\\beta\n$$\n\n**假设MLR.4’ 零均值和零相关**\n\n对所有的$j$,都有$\\mathbb{E}u=0$和$Cov(x_j,u)=0$\n\n这是一个比MLR.4更弱的假定,它只要求每个$x_j$与$u$无关。\n\n这导致$x_j$的非线性函数可能与误差相关\n\n**OLS的不一致性**\n\n如果误差与任何一个自变量相关,那么OLS就是有偏而不一致的估计。随着样本容量的增大,偏误将持续存在。\n\n$$\nplim \\hat{\\beta_1}-\\beta_1=\\frac{Cov(x_1,u)}{Var(x_1)}\n$$\n\n不一致性用总体的性质表示,而偏误则基于样本的对应量表示\n\n## 渐近正态和大样本推断\n\n**Theory** OLS的渐进正态性\n\n在MLR1-5下,\n\n1. \n$\\sqrt{n}(\\hat{\\beta}\\_j-\\beta\\_j)\\xrightarrow x N(0,\\sigma^2/a\\_j^2),a\\_j^2=plim(n^{-1}\\sum_{i=1}^n \\hat{r\\_{ij}}^2)$,其中$\\hat{r}\\_{ij}$是$x\\_j$对其余自变量回归得到的残差,即不能被其他变量解释的部分,我们称$\\hat{\\beta}\\_j$是渐进正态分布的\n2. $\\hat{\\sigma}^2$是$\\sigma^2=Var(u)$的一个一致估计\n3. 对于每个$j$都有$(\\hat{\\beta}_j-\\beta_j)/sd(\\hat{\\beta}_j)\\xrightarrow x N(0,1)$,且$(\\hat{\\beta}_j-\\beta_j)/se(\\hat{\\beta}_j)\\xrightarrow x N(0,1)$\n\n去掉了MLR.6,只需要有限方差且零均值与同方差性质\n\n总体分布恒定,与样本数量大小没有关系\n\n$\\hat{\\beta}_j$的估计方差:$\\hat{Var(\\hat{\\beta}_j)}=\\frac{\\hat{\\sigma}^2}{SST_j(1-R_j^2)}$,以$1/n$的速度收缩至零\n\n### 拉格朗日乘数LM统计量\n\n1. 将$y$对施加限制后的自变量集回归,保存残差$\\tilde{u}$\n2. 将$\\tilde{u}$对所有自变量进行回归,得到$R_u^2$\n3. 计算$LM=nR_u^2$\n4. 将LM与$\\chi_q^2$分布中适当的临界值$c$比较,如果$LM>c$,则拒绝原假设,说明后$q$个变量的系数不为零\n\n## OLS的渐近有效性\n\n在模型$y=\\beta_0+\\beta_1x_1+u$中,在MLR.4假设下,$\\mathbb{E}[u\\vert x]=0$,我们关注斜率\n\n令$z_i=g(x_i)$,$g$为任意函数,那么$u$就与$g(x)$无关。假定$Cov(z,x)\\neq 0$,那么,估计量\n\n$$\n\\tilde{\\beta}_1=\\sum(z_i-\\bar{z})y_i/\\sum (z_i-\\bar{z})x_i\n$$\n\n是对$\\beta_1$的一致估计。(证明:在分子分母分别除n并使用大数定律)\n\n$$\nplim \\tilde{\\beta_1}=\\beta_1+Cov(z,u)/Cov(z,x)=\\beta_1\n$$\n\n**Theory** OlS的渐近有效性\n\n高斯-马尔可夫假设下,OLS估计量具有最小的渐近方差,\n\n$$\nAvar \\sqrt{n}(\\hat{\\beta}_j-\\beta_j)\\le Avar\\sqrt{n}(\\tilde{\\beta}_j-\\beta_j)\n$$\n\n# 深入专题\n\n## 数据测度单位对 OLS 统计量的影晌\n\n度量单位对系数、标准误、置信区间、t统计量、F统计量的影响不会影响结果。\n\n**$\\beta$系数**\n\n将所有变量都标准化后的回归结果得到的系数称为标准化系数或$\\beta$系数 $\\hat{b}_j=(\\delta_j/\\delta_y)\\hat{\\beta}_j$\n\n由此得到的$\\beta$系数大小更具有说服力\n\n## 函数形式的进一步讨论\n\n### 对数函数\n\n$\\log(y)=\\hat{\\beta}_0+\\hat{\\beta}_1\\log x_1+\\hat{\\beta}_2x_2$\n\n固定$x_1$不变,有$\\Delta \\hat{\\log y}=\\hat{\\beta}_2 \\Delta x_2$,即$\\%\\Delta\\hat{y}=100\\cdot[\\exp(\\hat{\\beta}_2\\Delta x_2)-1]$是精确的预测变化百分比,它是一致的,但却不是无偏的,因为指数函数的非线性\n\n**对数的好处:**\n\n1. 斜率系数不随测度单位而变化,所以我们可以忽略以对数形式出现的变量的度量单位\n2. 严格为正的变量,条件分布常常具有异方差性或偏态性,取对数后可以降低\n3. 对数通常可以缩小变量的取值范围,对极端值也没有那么敏感\n\n**问题:**\n\n1. 变量在0、1之间时,会导致变换后的数据绝对值很大\n2. 更加难以预测原变量的值。两者的$R^2$也不具有可比性\n\n### 含二次式的模型\n\n一次项导致的变化表达式要重写,和变量本身也有关\n\n### 含有交互项的模型\n\n$y=\\beta_0+\\beta_1x_1+\\beta_2x_2+\\beta_3x_1x_2+u$$y=\\beta_0+\\beta_1x_1+\\beta_2x_2+\\beta_2x_1x_2+u$\n\n此时$\\beta_2$是$x_1=0$时$x_2$对$y$的偏效应,没什么意义\n\n$y=\\beta_0+\\beta_1x_1+\\beta_2x_2+\\beta_3(x_1-\\mu_1)(x_2-\\mu_2)+u$\n\n这样就是在均值处的偏效应了\n\n## 拟合优度和回归元选择的进一步探讨\n\n较小的$R^2$意味着误差方差相对$y$的方差太大了,以及我们很难精确地估计$\\beta_j$,但大样本容量可以抵消较大的误差方差。\n\n### 调整$R^2$\n\n$R^2=1-\\frac{SSR/n}{SST/n}$\n\n总体$R^2$定义为$1-\\sigma_u^2/\\sigma_y^2$,这是$y$的变化在总体中可以用自变量解释的部分比例,是我们希望用$R^2$估计的值\n\n但是用$SSR/n$估计$\\sigma_u^2$是有偏的,用$\\hat{\\sigma}^2=SSR/(n-k-1)$显然更好,同理,用$SST/(n-1)$代替$SST/n$\n\n由此,得到调整$R^2$:\n\n$\\bar{R^2}=1-\\hat{\\sigma}^2/[SST/(n-1)]=1-(1-R^2)\\frac{n-1}{n-k-1}$\n\n虽然两个无偏估计的比不是无偏估计,但是$\\bar{R^2}$在模型中额外增加自变量时施加了惩罚,在回归中增加一个变量时,只有新变量的t统计量大于1,$\\bar{R^2}$才会提高,增加一组变量时,联合检验显著的F统计量大于1才会提高\n\n### 利用调整$R^2$在两个非嵌套模型 (nonnested) 中进行选择\n\nDefinition: 两个方程没有哪一个是另一个的特殊情形,所以它们是非嵌套模型\n\n在这种情况下,使用普通$R^2$对自变量较少的模型不公平\n\n当自变量组对应着不同的函数形式时,调整$R^2$也是有价值的\n\n遗憾的是,**不能**通过拟合优度决定不同的因变量形式,因为它们的总变化是不同的,拟合的是两个完全不同的因变量\n\n**回归分析中控制过多的因素**\n\n注重对回归做其他条件不变的解释即可\n\n**增加回归元以减少误差方差**\n\n增加适当的无关变量可以减小误差方差,在大样本容量的情况下,所有OLS估计量对标准误都会减小\n\n## 预测和残差分析\n\n### 预测的置信区间\n\n估计方程:$\\hat{y}=\\hat{\\beta}_0+\\hat{\\beta}_1x_1+\\hat{\\beta}_2x_2+\\dots$\n\n$\\theta_0=\\beta_0+\\beta_1c_1+\\beta_2c_2+\\dots$ 的估计量是:\n\n$\\hat{\\theta}_0=\\hat{\\beta}_0+\\hat{\\beta}_1c_1+\\hat{\\beta}_2c_2+\\dots$ 我们关注它的置信区间\n\n在$df$较大的情况下,我们可以利用经验法则$\\hat{\\theta}_0\\pm2\\cdot se(\\hat{\\theta}_0)$构造95%置信区间\n\n求$se(\\hat{\\theta}_0)$:\n\n$\\theta_0$表达式代入方程:$y=\\theta_0+\\beta_1(x_1-c_1)+\\beta_2(x_2-c_2)+\\dots$\n\n用样本回归一下就可以了,截距项是预测值,还可以得到标准误\n\n由于每个解释变量的样本均值都为零时,截距估计量的方差最小,所以当$x_j$都取均值时,预测值的方差最小。随着$c_j$的值离中心越来越远,误差越来越大\n\n令$y^0$表示我们构造一个置信区间(预测区间)的估计值\n\n$$\n\\hat{y}^0=\\hat{\\beta}_0+\\hat{\\beta}_1x_1^0+\\cdots+\\\\\\\\\\hat{e}^0=y^0-\\hat{y}^0=\\beta_0+\\beta_1x_1^0+\\cdots+u^0-\\hat{y}^0\\\\\\\\\\mathbb{E}\\hat{e}^0=0\n$$\n\n所以预测误差的期望值为零\n\n$u^0$与用来得到$\\hat{\\beta}_j$的样本方差不相关,$u^0$与每个$\\hat{\\beta}_j$都不相关,所以$u^0$与$\\hat{y}^0$不相关\n\n$$\nVar(\\hat{e}^0)=Var(\\hat{y}^0)+Var(u^0)=Var(\\hat{y}^0)+\\sigma^2\n$$\n\n第一项来自抽样误差,即对$\\beta_j$的估计误差\n\n$se(\\hat{e}^0)=\\sqrt{se(\\hat{y}^0)^2+\\hat{\\sigma}^2}$\n\n### 残差分析\n\n计算剔除某些因素后样本的水平\n\n### 因变量为$\\log y$时对$y$的预测\n\n$\\hat{y}=\\exp(\\hat{\\log y})?$ 会系统地**低估**$y$的预测值\n\n$\\mathbb{E}[y\\vert x]=\\exp(\\sigma^2/2)\\cdot \\exp(\\beta_0+\\beta_1x_1+\\beta_2x_2+\\dots)$\n\n$\\hat{y}=\\exp(\\hat{\\sigma}^2/2)\\exp(\\hat{\\log y})$,虽然不是无偏的,但是是一致的。它依赖于$u$的正态性\n\n一般的情况,$\\mathbb{E}[y\\vert x]=\\alpha_0\\cdot \\exp(\\beta_0+\\beta_1x_1+\\beta_2x_2+\\dots)$,$\\alpha_0$是$\\exp(u)$的期望值,且是大于一的,所以我们要求$\\hat{\\alpha}_0$\n\n矩估计$\\hat{\\alpha}\\_0=\\frac{1}{n}\\sum\\exp(\\hat{u}\\_i)$,是一个一致有偏的估计量,这是所谓的污染估计值的一种特殊形式。或者我们可以通过一个过原点的简单回归:$m\\_i=\\exp(\\beta\\_0+\\beta\\_1x\\_{i1}+\\beta\\_2x\\_{i2}+\\dots),\\mathbb{E}[y\\_i\\vert m\\_i]=\\alpha\\_0m\\_i$,这样,我们就能从$y_i$对$\\hat{m}_i$的回归中得到一个$\\alpha_0$的无偏估计:\n\n$$\n\\tilde{\\alpha}_0=\\frac{\\sum\\hat{m}_iy_i}{\\sum\\hat{m}_i^2}\n$$\n\n**拟合优度**\n\n在普通最小二乘中,$R^2$就是$\\hat{y}_i$与$y_i$之间的相关系数的平方,如果我们对所有观测量都计算$\\hat{y}_i=\\hat{\\alpha}_0m_i$,由于是在变量上乘了一个常数$\\hat{\\alpha}_0$,所以对$\\alpha_0$的估计不会影响到结果。我们还是计算$y\n_i$和$\\hat{y}\n_i$的相关系数,这样就可以在不同的因变量模型之间对比拟合优度\n\n# 含有定性信息的多元回归分析: 二值(或虚拟)变量\n\n本部分在劳动经济学中较多涉及,不再赘述","slug":"OLS method","published":1,"updated":"2022-04-19T07:57:01.732Z","_id":"cl24gxm3z0000x6pkhpk029qg","comments":1,"photos":[],"link":"","content":"<head>\n <script src=\"https://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML\" type=\"text/javascript\"></script>\n <script type=\"text/x-mathjax-config\">\n MathJax.Hub.Config({\n tex2jax: {\n skipTags: ['script', 'noscript', 'style', 'textarea', 'pre'],\n inlineMath: [['$','$']]\n }\n });\n </script>\n</head>\n\n<h1 id=\"简单回归模型\"><a href=\"#简单回归模型\" class=\"headerlink\" title=\"简单回归模型\"></a>简单回归模型</h1><p>$y=\\beta_0+\\beta_1 x+u$</p>\n<p>$x$ 和$u$ 的相关性?</p>\n<p>关键假定是,$u$ 的平均值与$x$ 无关,即$\\mathbb{E}[u\\vert x]=\\mathbb{E}u$,称之为<strong>均值独立</strong></p>\n<p>$\\mathbb{E}[u\\vert x]=\\mathbb{E}u=0$ 称之为零条件均值假定,等于$0$定义了截距</p>\n<p>$\\mathbb{E}[y\\vert x]=\\beta_0+\\beta_1x$ 总体回归函数</p>\n<h2 id=\"普通最小二乘法的推导\"><a href=\"#普通最小二乘法的推导\" class=\"headerlink\" title=\"普通最小二乘法的推导\"></a>普通最小二乘法的推导</h2><p>$$<br>\\mathbb{E}[y-\\beta_1x-\\beta_0]=0\\\\\\mathbb{E}[x(y-\\beta_1x-\\beta_0)]=0<br>$$</p>\n<p>利用零条件均值假定,以及矩估计,或者使残差平方和最小,即可获得OLS一阶条件</p>\n<p>$$<br>\\begin{align*}\\sum y_i-\\hat{\\beta_0}-\\hat{\\beta_1}x_i=0\\\\\\sum x_i(y_i-\\hat{\\beta_0}-\\hat{\\beta_1}x_i)=0\\end{align*}<br>$$</p>\n<p>OLS回归线/样本回归函数:$\\hat{y}=\\hat{\\beta_0}+\\hat{\\beta_1}x$,是总体回归函数的一个样本估计,总体回归函数始终是未知的。</p>\n<h2 id=\"统计量的性质\"><a href=\"#统计量的性质\" class=\"headerlink\" title=\"统计量的性质\"></a>统计量的性质</h2><p>$\\sum \\hat{u}_i=0$, $\\sum x_i\\hat{u}_i=0$ 这其实就是一阶条件</p>\n<p>定义:</p>\n<p>总平方和SST,解释平方和SSE,残差平方和SSR</p>\n<p>$SST=\\sum(y_i-\\bar{y})^2$</p>\n<p>$SSE=\\sum (\\hat{y}_i-\\bar{y})^2$</p>\n<p>$SSR=\\sum \\hat{u}_i^2$</p>\n<p>SST=SSE+SSR</p>\n<p>拟合优度$R^2=SSE/SST$,是可解释的波动与总波动之比</p>\n<h2 id=\"OLS估计量的期望和方差\"><a href=\"#OLS估计量的期望和方差\" class=\"headerlink\" title=\"OLS估计量的期望和方差\"></a>OLS估计量的期望和方差</h2><h3 id=\"OLS的无偏性\"><a href=\"#OLS的无偏性\" class=\"headerlink\" title=\"OLS的无偏性\"></a>OLS的无偏性</h3><p><strong>SLR.1</strong> 线性与参数</p>\n<p><strong>SLR.2</strong> 随机抽样,实践过程中,并不是所有横截面样本都可以看成是随机抽样的结果</p>\n<p>$y_i=\\beta_0+\\beta_1x_i+u_i$,其中$u_i$是第$i$ 次观测的误差或干扰,与残差不同 </p>\n<p><strong>SLR.3</strong> 解释变量的样本有波动</p>\n<p>$x$ 的样本结果不是完全相同的数值</p>\n<p><strong>SLR.4</strong> 零条件均值</p>\n<p><strong>下面证明OLS的无偏性</strong></p>\n<p>$\\hat{\\beta}_1=\\frac{\\sum(x_i-\\bar{x})y_i}{\\sum(x_i-\\bar{x})^2}=\\frac{\\sum(x_i-\\bar{x})y_i}{SST_x}=\\frac{\\sum(x_i-\\bar{x})(\\beta_0+\\beta_1x_i+u_i)}{SST_x}=\\beta_1+\\frac{\\sum d_iu_i}{SST_x}$,其中$d_i=x_i-\\bar{x}$</p>\n<p>因此,$\\mathbb{E}\\hat{\\beta}_1=\\beta_1,\\mathbb{E}\\hat{\\beta}_0=\\beta_0$</p>\n<p>无偏性是抽样分布的性质,并不能确定从特定样本中得到的估计值</p>\n<p>时序分析中将会放松SLR.2</p>\n<p><strong>SLR.5</strong> 同方差性</p>\n<p>$Var(u\\vert x)=\\sigma^2$</p>\n<p>$\\sigma^2=\\mathbb{E}[u^2\\vert x]$,即$\\sigma^2$是$u$的无条件方差,也经常被成为误差方差或干扰方差</p>\n<p>若$Var(u\\vert x)$取决于$x$,则误差项表现出异方差性</p>\n<p><strong>定理 OLS估计量的抽样方差</strong></p>\n<p>在SLR.1-SLR.5条件下,对于样本值:</p>\n<p>$Var(\\hat{\\beta}_1)=\\frac{\\sigma^2}{SST_x}$</p>\n<p>$Var(\\hat{\\beta}_0)=\\frac{\\sigma^2\\bar{x}}{SST_x}+\\frac{\\sigma^2}{n}$</p>\n<p>从$\\hat{\\beta}_1=\\beta_1+\\frac{\\sum d_iu_i}{SST_x}$出发,$Var(\\hat{\\beta}_1)=\\frac{\\sum d_i^2\\sigma^2}{SST_x^2}=\\sigma^2/SST_x$</p>\n<p>一个小结论:</p>\n<p>$\\sum x_i^2\\ge\\sum(x_i-\\bar{x})^2$</p>\n<p><strong>误差方差的估计</strong></p>\n<p>$\\hat{u}_i=u_i-(\\hat{\\beta}_0-\\beta_0)-(\\hat{\\beta}_1-\\beta_1)x_i$</p>\n<p>$\\sigma^2$的一个无偏“估计量”是$\\sum u_i^2/n$ 但$u_i$不可观测</p>\n<p>OLS有两个约束条件,因此:</p>\n<p>$\\hat{\\sigma}^2=SSR/(n-2)$ 是一个无偏估计,有时记为$s^2$</p>\n<p>$$<br>0=\\bar{u}-(\\hat{\\beta}_0-\\beta_0)-(\\hat{\\beta}_1-\\beta_1)\\bar{x}\\\\\\sum\\hat{u}_i^2=\\sum(u_i-(\\hat{\\beta}_0-\\beta_0)-(\\hat{\\beta}_1-\\beta_1)x_i)^2\\\\=\\sum(u_i-\\bar{u}-(\\hat{\\beta}_1-\\beta_1)(x_i-\\bar{x}))^2<br>$$</p>\n<p>$sd(\\hat{\\beta}_1)=\\sigma/\\sqrt{SST}$它的一个比较自然的估计量就是$se(\\hat{\\beta}_1)=\\hat{\\sigma}/\\sqrt{SST}$,被称之为标准误(standard error)</p>\n<h1 id=\"多元回归分析:估计\"><a href=\"#多元回归分析:估计\" class=\"headerlink\" title=\"多元回归分析:估计\"></a>多元回归分析:估计</h1><h2 id=\"如何得到OLS估计值\"><a href=\"#如何得到OLS估计值\" class=\"headerlink\" title=\"如何得到OLS估计值\"></a>如何得到OLS估计值</h2><p>一阶条件:</p>\n<p>$$<br>\\sum(y_i-\\hat{\\beta}_0-\\hat{\\beta}_1x_{i1}-\\cdots)=0\\\\\\sum x_{i1}(y_i-\\hat{\\beta}_0-\\hat{\\beta}_1x_{i1}-\\cdots)=0\\\\\\vdots\\\\\\sum x_{ik}(y_i-\\hat{\\beta}_0-\\hat{\\beta}_1x_{i1}-\\cdots)=0<br>$$</p>\n<p>回归线或样本回归函数由截距估计值与斜率估计值组成</p>\n<p>估计值$\\hat{\\beta}_i$具有偏效应,因此多元回归使我们在对自变量的值不加限制的时候有效模拟施加限制的情况</p>\n<h2 id=\"拟合值和残差的重要性质\"><a href=\"#拟合值和残差的重要性质\" class=\"headerlink\" title=\"拟合值和残差的重要性质\"></a>拟合值和残差的重要性质</h2><ol>\n<li>残差样本平均值为零</li>\n<li>OLS拟合值和OLS残差之间的样本协方差为零</li>\n<li>样本平均在回归线上</li>\n</ol>\n<p>考虑$\\hat{y}=\\hat{\\beta}_0+\\hat{\\beta}_1x_1+\\hat{\\beta}_2x_2$,$\\hat{\\beta}_1$的一种表达形式是:$\\hat{\\beta}_1=\\frac{\\sum\\hat{r}_{i1}y_i}{\\sum\\hat{r}_{i1}^2}$</p>\n<p>其中$\\hat{r}_{i1} $是$x_1$对$x_2$的回归得到的OLS残差,即$x_{i1}$与$x_{i2}$中不相关的部分,所以$\\hat{\\beta}_1$就是排除了$x_2$影响后$y$与$x_1$之间的关系</p>\n<h3 id=\"简单回归与多元回归\"><a href=\"#简单回归与多元回归\" class=\"headerlink\" title=\"简单回归与多元回归\"></a>简单回归与多元回归</h3><p>$\\tilde{y}=\\tilde{\\beta}_0+\\tilde{\\beta}_1x_1$和$\\hat{y}=\\hat{\\beta}_0+\\hat{\\beta}_1x_1+\\hat{\\beta}_2x_2$的结果会有什么关系?</p>\n<p>令$\\bar{\\delta}$是$x_2$对$x_1$的简单回归斜率,则$\\tilde{\\beta}_1=\\hat{\\beta}_1+\\hat{\\beta}_2\\bar{\\delta}$</p>\n<p><strong>拟合优度相关的内容和简单线性回归一致</strong></p>\n<p>增加一个自变量之后$R^2$不会减小,而且通常会增大</p>\n<h2 id=\"OLS估计量的期望\"><a href=\"#OLS估计量的期望\" class=\"headerlink\" title=\"OLS估计量的期望\"></a>OLS估计量的期望</h2><p><strong>MLR.1</strong> 线性于参数</p>\n<p><strong>MLR.2</strong> 随机抽样</p>\n<p><strong>MLR.3</strong> 不存在完全共线性</p>\n<p><strong>MLR.4</strong> 条件均值为零</p>\n<p>当MLR.4成立时,我们说具有外生解释变量,如果$x_j$与$u$相关,那么$x_j$称之为内生解释变量</p>\n<p>限制了无法观测的因素与解释变量之间的关系</p>\n<p>在MLR1-4条件下,可以证明OLS的无偏性$\\mathbb{E}\\hat{\\beta}_i=\\beta_i$</p>\n<p>包含无关变量一般不会对OLS的无偏性产生影响,但是会对方差产生不利影响</p>\n<p><strong>遗漏变量偏误</strong></p>\n<p>总体模型:$y=\\beta_0+\\beta_1x_1+\\beta_2x_2+\\beta_3x_3+u$</p>\n<p>遗漏变量后的估计模型:$\\tilde{y}=\\tilde{\\beta}_0+\\tilde{\\beta}_1x_1+\\tilde{\\beta}_2x_2$</p>\n<p><strong>假设$x_2$和$x_3$无关,$x_1$和$x_3$相关</strong></p>\n<p>$$<br>\\mathbb{E}\\tilde{\\beta}_1=\\beta_1+\\beta_3\\frac{\\sum x_{i3}(x_{i1}-\\bar{x}_1)}{\\sum (x_{i1}-\\bar{x}_1)^2}<br>$$</p>\n<p><strong>MLR.5</strong> 同方差性 $Var[u\\vert x_1,x_2,\\dots,x_k]=\\sigma^2$</p>\n<p>即以解释变量为条件,不管解释变量出现怎样的组合,误差项的方差都是一样的。如果不成立称之为异方差性</p>\n<p>MLR1-5称之为横截面回归的<strong>高斯-马尔可夫</strong>假定</p>\n<p>$Var\\hat{\\beta}_i=\\frac{\\sigma^2}{SST_j(1-R_j^2)}$,其中$R_j$来自于$x_j$对其他变量回归得到的$R^2$,需要MLR.5的的成立</p>\n<p>两个或多个自变量之间高度但不完全相关称之为<strong>多重共线性</strong>,即$R_j^2$接近于1,但这并不违反MLR.3,最终的问题还是要看$\\hat{\\beta}_j$与自身的标准差的大小关系</p>\n<p>很小的$SST_j$也可以导致大方差,即小样本容量会导致很大的抽样方差</p>\n<p>如果存在相关性的自变量和我们关注的自变量没有高度相关,其实没有直接影响,就不必关心这种共线性</p>\n<p>误设模型中的方差</p>\n<p>$Var\\hat{\\beta}_i=\\frac{\\sigma^2}{SST_j(1-R_j^2)}$,和$Var\\tilde{\\beta}_i=\\frac{\\sigma^2}{SST_j}$</p>\n<p>若$\\beta_2\\neq0$,则简单模型给出方差更小的有偏估计;若$\\beta_2=0$,则简单模型给出方差更小的无偏估计。</p>\n<p>直觉上讲,如果$x_2$对$y$没有偏效应,在回归中加入$x_2$只会加剧多重共线性。如果$\\beta_2\\neq0$,则偏误不会随着样本容量扩大而减小,但是Var会随着样本容量增大而趋于零,因此增加自变量导致的多重共线性就会变得没那么重要,大样本情况下倾向使用更复杂的模型</p>\n<h3 id=\"OLS估计的标准误\"><a href=\"#OLS估计的标准误\" class=\"headerlink\" title=\"OLS估计的标准误\"></a>OLS估计的标准误</h3><p>$$<br>\\hat{\\sigma}^2=\\frac{\\sum u_i^2}{n-k-1}=\\frac{SSR}{n-k-1}<br>$$</p>\n<p>自由度$df=n-k-1$</p>\n<p>可以证明,$\\mathbb{E}\\hat{\\sigma}^2=\\sigma^2$</p>\n<p>$\\hat{\\sigma}=\\sqrt{\\hat{\\sigma}^2}$称之为回归标准误SER,是误差项的标准差的估计量,还被称之为估计值标准误和均方误差</p>\n<p>$se(\\hat{\\beta}_i)=\\frac{\\hat{\\sigma}^2}{\\sqrt{SST_j(1-R_j)^2}}$</p>\n<p>异方差性质不会导致参数估计偏误,但是会导致$Var(\\hat{\\beta}_j)$出现问题,导致标准误无效</p>\n<h2 id=\"OLS的有效性\"><a href=\"#OLS的有效性\" class=\"headerlink\" title=\"OLS的有效性\"></a>OLS的有效性</h2><p>在MLR1-5的假定下,OKS估计量是最优线性无偏估计量BLUE,即具有最小的方差。尤其是MLR.5,保证了OLS在线性无偏估计量中具有最小的方差</p>\n<h1 id=\"多元回归分析:推断\"><a href=\"#多元回归分析:推断\" class=\"headerlink\" title=\"多元回归分析:推断\"></a>多元回归分析:推断</h1><h2 id=\"OLS估计量的抽样分布\"><a href=\"#OLS估计量的抽样分布\" class=\"headerlink\" title=\"OLS估计量的抽样分布\"></a>OLS估计量的抽样分布</h2><p><strong>MLR.6</strong> 正态性 总体误差$u$独立于解释变量,并且服从均值为零,方差为$\\sigma^2$的正态分布</p>\n<p>MLR1-6称之为经典线性模型(CLM)假定。在CLM下,OLS是最小方差的无偏估计,不必限制在线性估计中</p>\n<p>由千于$u$ 是影响着 $y$ 而又观测不到的许多因素之和,所以我们可借助中心极限定理断定 $u$ 具有近似正态分布</p>\n<p>通常我们可以利用某种变换得到一个$u$接近于正态的分布</p>\n<p>误差项的正态性导致了OLS估计量的正态抽样分布</p>\n<p>$$<br>\\frac{\\hat{\\beta}_j-\\beta_j}{sd(\\hat{\\beta}_j)}\\sim Normal(0,1)<br>$$</p>\n<h2 id=\"对单个总体参数的检验:t检验\"><a href=\"#对单个总体参数的检验:t检验\" class=\"headerlink\" title=\"对单个总体参数的检验:t检验\"></a>对单个总体参数的检验:t检验</h2><p>在CLM假定下,$\\frac{\\hat{\\beta}_j-\\beta_j}{se(\\hat{\\beta}_j)}\\sim t_{n-k-1}$</p>\n<p>多数应用中,主要兴趣在于检验原假设$H_0:\\beta_j=0$</p>\n<p>为什么不反过来写?因为$x_j$对$y$有偏效应的表述对$\\beta_j$不为零对任何一个值都成立</p>\n<p>$t_{\\hat{\\beta}_j}=\\hat{\\beta}_j/se(\\hat{\\beta}_j)$称之为t统计量</p>\n<p><strong>单侧/双侧备择假设,t检验p值 ,置信区间</strong></p>\n<p>参考概统知识,此处不表</p>\n<h2 id=\"检验关于参数的一个线性组合假设\"><a href=\"#检验关于参数的一个线性组合假设\" class=\"headerlink\" title=\"检验关于参数的一个线性组合假设\"></a>检验关于参数的一个线性组合假设</h2><p>$H_0:\\beta_1=\\beta_2$ 如何检验?</p>\n<p>$t=\\frac{\\hat{\\beta}_1-\\hat{\\beta}_2}{se(\\hat{\\beta}_1-\\hat{\\beta}_2)}$,关键是求解标准误,即要求解$Cov(\\hat{\\beta}_1,\\hat{\\beta}_2)$的一个估计值,这在数学上是复杂的</p>\n<p>但我们可以改写模型$\\beta_1=\\theta_1+\\beta_2$</p>\n<p>$y=\\beta_0+(\\theta_1+\\beta_2)x_1+\\beta_2x_2+u=\\beta_0+\\theta_1x_1+\\beta_2(x_1+x_2)+u$</p>\n<p>直接检验$\\theta_1$即可</p>\n<h2 id=\"对多个线性约束对检验:F检验\"><a href=\"#对多个线性约束对检验:F检验\" class=\"headerlink\" title=\"对多个线性约束对检验:F检验\"></a>对多个线性约束对检验:F检验</h2><p>原假设:$H_0:\\beta_{k-q+1}=0,\\dots\\beta_k=0$</p>\n<p>不含$\\beta_{\\dots}$的模型是受约束模型,原始模型称之为不受约束模型</p>\n<p>受约束模型增加了$q$个排除性约束,定义$F$统计量</p>\n<p>$$<br>F=\\frac{(SSR_r-SSR_{ur})/q}{SSR_{ur}/(n-k-1)}=\\frac{(R_{ur}^2-R_r^2)/q}{(1-R_{ur}^2)/df_{ur}}\\sim F_{q,n-k-1}<br>$$</p>\n<p>其中$SSR_r$是受约束模型的残差平方和,$SSR_{ur}$是不受约束的残差平方和,$q=df_r-df_{ur}$</p>\n<p>如果拒绝原假设,那么就说$x_{k-q+1},\\dots x_k$ 在适当的显著性水平上是联合统计显著的</p>\n<p><strong>对于一般的线性约束</strong></p>\n<p>如指定了$\\beta_1=1$,则将$x_1$挪到回归方程左边</p>\n<p>由于两次的因变量不同,不能采用$R^2$形式的统计量</p>\n<h1 id=\"多元回归分析:OLS的渐进性\"><a href=\"#多元回归分析:OLS的渐进性\" class=\"headerlink\" title=\"多元回归分析:OLS的渐进性\"></a>多元回归分析:OLS的渐进性</h1><h2 id=\"一致性\"><a href=\"#一致性\" class=\"headerlink\" title=\"一致性\"></a>一致性</h2><p>直观的理解:当样本量趋于无穷时,收敛到真值</p>\n<p><strong>Theory OLS</strong>的一致性</p>\n<p>在MLR1-4下,$\\hat{\\beta}_j$是$\\hat{\\beta}_j$的一致估计</p>\n<p><em>PROOF</em></p>\n<p>$$<br>X\\beta+u=y\\\\\\hat{\\beta}=(X^TX)^{-1}X^Ty=(X^TX)^{-1}X^T(X\\beta+u)\\\\=\\beta+(X^TX)^{-1}X^Tu=\\beta+(\\frac{1}{n}\\sum_{i=1}^n x_i^Tx_i)^{-1}(\\frac{1}{n}\\sum _{i=1}^nx_i^Tu)<br>$$</p>\n<p>according to the large number law:</p>\n<p>$$<br>\\frac{1}{n}\\sum x_i^Tx_i\\xrightarrow{p}\\mathbb{E}x_i^Tx_i=A,\\quad \\frac{1}{n}\\sum x_i^T u\\xrightarrow{p}\\mathbb{E}x_iu=0<br>$$</p>\n<p>because $A$ is a nonsingular matrix, so$(\\frac{1}{n}\\sum x_i^Tx_i)^{-1}\\xrightarrow{p}A^{-1}$</p>\n<p>$$<br>plim \\hat{\\beta}=\\beta+A^{-1}\\cdot0=\\beta<br>$$</p>\n<p><strong>假设MLR.4’ 零均值和零相关</strong></p>\n<p>对所有的$j$,都有$\\mathbb{E}u=0$和$Cov(x_j,u)=0$</p>\n<p>这是一个比MLR.4更弱的假定,它只要求每个$x_j$与$u$无关。</p>\n<p>这导致$x_j$的非线性函数可能与误差相关</p>\n<p><strong>OLS的不一致性</strong></p>\n<p>如果误差与任何一个自变量相关,那么OLS就是有偏而不一致的估计。随着样本容量的增大,偏误将持续存在。</p>\n<p>$$<br>plim \\hat{\\beta_1}-\\beta_1=\\frac{Cov(x_1,u)}{Var(x_1)}<br>$$</p>\n<p>不一致性用总体的性质表示,而偏误则基于样本的对应量表示</p>\n<h2 id=\"渐近正态和大样本推断\"><a href=\"#渐近正态和大样本推断\" class=\"headerlink\" title=\"渐近正态和大样本推断\"></a>渐近正态和大样本推断</h2><p><strong>Theory</strong> OLS的渐进正态性</p>\n<p>在MLR1-5下,</p>\n<p>1.<br>$\\sqrt{n}(\\hat{\\beta}_j-\\beta_j)\\xrightarrow x N(0,\\sigma^2/a_j^2),a_j^2=plim(n^{-1}\\sum_{i=1}^n \\hat{r_{ij}}^2)$,其中$\\hat{r}_{ij}$是$x_j$对其余自变量回归得到的残差,即不能被其他变量解释的部分,我们称$\\hat{\\beta}_j$是渐进正态分布的<br>2. $\\hat{\\sigma}^2$是$\\sigma^2=Var(u)$的一个一致估计<br>3. 对于每个$j$都有$(\\hat{\\beta}_j-\\beta_j)/sd(\\hat{\\beta}_j)\\xrightarrow x N(0,1)$,且$(\\hat{\\beta}_j-\\beta_j)/se(\\hat{\\beta}_j)\\xrightarrow x N(0,1)$</p>\n<p>去掉了MLR.6,只需要有限方差且零均值与同方差性质</p>\n<p>总体分布恒定,与样本数量大小没有关系</p>\n<p>$\\hat{\\beta}_j$的估计方差:$\\hat{Var(\\hat{\\beta}_j)}=\\frac{\\hat{\\sigma}^2}{SST_j(1-R_j^2)}$,以$1/n$的速度收缩至零</p>\n<h3 id=\"拉格朗日乘数LM统计量\"><a href=\"#拉格朗日乘数LM统计量\" class=\"headerlink\" title=\"拉格朗日乘数LM统计量\"></a>拉格朗日乘数LM统计量</h3><ol>\n<li>将$y$对施加限制后的自变量集回归,保存残差$\\tilde{u}$</li>\n<li>将$\\tilde{u}$对所有自变量进行回归,得到$R_u^2$</li>\n<li>计算$LM=nR_u^2$</li>\n<li>将LM与$\\chi_q^2$分布中适当的临界值$c$比较,如果$LM>c$,则拒绝原假设,说明后$q$个变量的系数不为零</li>\n</ol>\n<h2 id=\"OLS的渐近有效性\"><a href=\"#OLS的渐近有效性\" class=\"headerlink\" title=\"OLS的渐近有效性\"></a>OLS的渐近有效性</h2><p>在模型$y=\\beta_0+\\beta_1x_1+u$中,在MLR.4假设下,$\\mathbb{E}[u\\vert x]=0$,我们关注斜率</p>\n<p>令$z_i=g(x_i)$,$g$为任意函数,那么$u$就与$g(x)$无关。假定$Cov(z,x)\\neq 0$,那么,估计量</p>\n<p>$$<br>\\tilde{\\beta}_1=\\sum(z_i-\\bar{z})y_i/\\sum (z_i-\\bar{z})x_i<br>$$</p>\n<p>是对$\\beta_1$的一致估计。(证明:在分子分母分别除n并使用大数定律)</p>\n<p>$$<br>plim \\tilde{\\beta_1}=\\beta_1+Cov(z,u)/Cov(z,x)=\\beta_1<br>$$</p>\n<p><strong>Theory</strong> OlS的渐近有效性</p>\n<p>高斯-马尔可夫假设下,OLS估计量具有最小的渐近方差,</p>\n<p>$$<br>Avar \\sqrt{n}(\\hat{\\beta}_j-\\beta_j)\\le Avar\\sqrt{n}(\\tilde{\\beta}_j-\\beta_j)<br>$$</p>\n<h1 id=\"深入专题\"><a href=\"#深入专题\" class=\"headerlink\" title=\"深入专题\"></a>深入专题</h1><h2 id=\"数据测度单位对-OLS-统计量的影晌\"><a href=\"#数据测度单位对-OLS-统计量的影晌\" class=\"headerlink\" title=\"数据测度单位对 OLS 统计量的影晌\"></a>数据测度单位对 OLS 统计量的影晌</h2><p>度量单位对系数、标准误、置信区间、t统计量、F统计量的影响不会影响结果。</p>\n<p><strong>$\\beta$系数</strong></p>\n<p>将所有变量都标准化后的回归结果得到的系数称为标准化系数或$\\beta$系数 $\\hat{b}_j=(\\delta_j/\\delta_y)\\hat{\\beta}_j$</p>\n<p>由此得到的$\\beta$系数大小更具有说服力</p>\n<h2 id=\"函数形式的进一步讨论\"><a href=\"#函数形式的进一步讨论\" class=\"headerlink\" title=\"函数形式的进一步讨论\"></a>函数形式的进一步讨论</h2><h3 id=\"对数函数\"><a href=\"#对数函数\" class=\"headerlink\" title=\"对数函数\"></a>对数函数</h3><p>$\\log(y)=\\hat{\\beta}_0+\\hat{\\beta}_1\\log x_1+\\hat{\\beta}_2x_2$</p>\n<p>固定$x_1$不变,有$\\Delta \\hat{\\log y}=\\hat{\\beta}_2 \\Delta x_2$,即$%\\Delta\\hat{y}=100\\cdot[\\exp(\\hat{\\beta}_2\\Delta x_2)-1]$是精确的预测变化百分比,它是一致的,但却不是无偏的,因为指数函数的非线性</p>\n<p><strong>对数的好处:</strong></p>\n<ol>\n<li>斜率系数不随测度单位而变化,所以我们可以忽略以对数形式出现的变量的度量单位</li>\n<li>严格为正的变量,条件分布常常具有异方差性或偏态性,取对数后可以降低</li>\n<li>对数通常可以缩小变量的取值范围,对极端值也没有那么敏感</li>\n</ol>\n<p><strong>问题:</strong></p>\n<ol>\n<li>变量在0、1之间时,会导致变换后的数据绝对值很大</li>\n<li>更加难以预测原变量的值。两者的$R^2$也不具有可比性</li>\n</ol>\n<h3 id=\"含二次式的模型\"><a href=\"#含二次式的模型\" class=\"headerlink\" title=\"含二次式的模型\"></a>含二次式的模型</h3><p>一次项导致的变化表达式要重写,和变量本身也有关</p>\n<h3 id=\"含有交互项的模型\"><a href=\"#含有交互项的模型\" class=\"headerlink\" title=\"含有交互项的模型\"></a>含有交互项的模型</h3><p>$y=\\beta_0+\\beta_1x_1+\\beta_2x_2+\\beta_3x_1x_2+u$$y=\\beta_0+\\beta_1x_1+\\beta_2x_2+\\beta_2x_1x_2+u$</p>\n<p>此时$\\beta_2$是$x_1=0$时$x_2$对$y$的偏效应,没什么意义</p>\n<p>$y=\\beta_0+\\beta_1x_1+\\beta_2x_2+\\beta_3(x_1-\\mu_1)(x_2-\\mu_2)+u$</p>\n<p>这样就是在均值处的偏效应了</p>\n<h2 id=\"拟合优度和回归元选择的进一步探讨\"><a href=\"#拟合优度和回归元选择的进一步探讨\" class=\"headerlink\" title=\"拟合优度和回归元选择的进一步探讨\"></a>拟合优度和回归元选择的进一步探讨</h2><p>较小的$R^2$意味着误差方差相对$y$的方差太大了,以及我们很难精确地估计$\\beta_j$,但大样本容量可以抵消较大的误差方差。</p>\n<h3 id=\"调整-R-2\"><a href=\"#调整-R-2\" class=\"headerlink\" title=\"调整$R^2$\"></a>调整$R^2$</h3><p>$R^2=1-\\frac{SSR/n}{SST/n}$</p>\n<p>总体$R^2$定义为$1-\\sigma_u^2/\\sigma_y^2$,这是$y$的变化在总体中可以用自变量解释的部分比例,是我们希望用$R^2$估计的值</p>\n<p>但是用$SSR/n$估计$\\sigma_u^2$是有偏的,用$\\hat{\\sigma}^2=SSR/(n-k-1)$显然更好,同理,用$SST/(n-1)$代替$SST/n$</p>\n<p>由此,得到调整$R^2$:</p>\n<p>$\\bar{R^2}=1-\\hat{\\sigma}^2/[SST/(n-1)]=1-(1-R^2)\\frac{n-1}{n-k-1}$</p>\n<p>虽然两个无偏估计的比不是无偏估计,但是$\\bar{R^2}$在模型中额外增加自变量时施加了惩罚,在回归中增加一个变量时,只有新变量的t统计量大于1,$\\bar{R^2}$才会提高,增加一组变量时,联合检验显著的F统计量大于1才会提高</p>\n<h3 id=\"利用调整-R-2-在两个非嵌套模型-nonnested-中进行选择\"><a href=\"#利用调整-R-2-在两个非嵌套模型-nonnested-中进行选择\" class=\"headerlink\" title=\"利用调整$R^2$在两个非嵌套模型 (nonnested) 中进行选择\"></a>利用调整$R^2$在两个非嵌套模型 (nonnested) 中进行选择</h3><p>Definition: 两个方程没有哪一个是另一个的特殊情形,所以它们是非嵌套模型</p>\n<p>在这种情况下,使用普通$R^2$对自变量较少的模型不公平</p>\n<p>当自变量组对应着不同的函数形式时,调整$R^2$也是有价值的</p>\n<p>遗憾的是,<strong>不能</strong>通过拟合优度决定不同的因变量形式,因为它们的总变化是不同的,拟合的是两个完全不同的因变量</p>\n<p><strong>回归分析中控制过多的因素</strong></p>\n<p>注重对回归做其他条件不变的解释即可</p>\n<p><strong>增加回归元以减少误差方差</strong></p>\n<p>增加适当的无关变量可以减小误差方差,在大样本容量的情况下,所有OLS估计量对标准误都会减小</p>\n<h2 id=\"预测和残差分析\"><a href=\"#预测和残差分析\" class=\"headerlink\" title=\"预测和残差分析\"></a>预测和残差分析</h2><h3 id=\"预测的置信区间\"><a href=\"#预测的置信区间\" class=\"headerlink\" title=\"预测的置信区间\"></a>预测的置信区间</h3><p>估计方程:$\\hat{y}=\\hat{\\beta}_0+\\hat{\\beta}_1x_1+\\hat{\\beta}_2x_2+\\dots$</p>\n<p>$\\theta_0=\\beta_0+\\beta_1c_1+\\beta_2c_2+\\dots$ 的估计量是:</p>\n<p>$\\hat{\\theta}_0=\\hat{\\beta}_0+\\hat{\\beta}_1c_1+\\hat{\\beta}_2c_2+\\dots$ 我们关注它的置信区间</p>\n<p>在$df$较大的情况下,我们可以利用经验法则$\\hat{\\theta}_0\\pm2\\cdot se(\\hat{\\theta}_0)$构造95%置信区间</p>\n<p>求$se(\\hat{\\theta}_0)$:</p>\n<p>$\\theta_0$表达式代入方程:$y=\\theta_0+\\beta_1(x_1-c_1)+\\beta_2(x_2-c_2)+\\dots$</p>\n<p>用样本回归一下就可以了,截距项是预测值,还可以得到标准误</p>\n<p>由于每个解释变量的样本均值都为零时,截距估计量的方差最小,所以当$x_j$都取均值时,预测值的方差最小。随着$c_j$的值离中心越来越远,误差越来越大</p>\n<p>令$y^0$表示我们构造一个置信区间(预测区间)的估计值</p>\n<p>$$<br>\\hat{y}^0=\\hat{\\beta}_0+\\hat{\\beta}_1x_1^0+\\cdots+\\\\\\hat{e}^0=y^0-\\hat{y}^0=\\beta_0+\\beta_1x_1^0+\\cdots+u^0-\\hat{y}^0\\\\\\mathbb{E}\\hat{e}^0=0<br>$$</p>\n<p>所以预测误差的期望值为零</p>\n<p>$u^0$与用来得到$\\hat{\\beta}_j$的样本方差不相关,$u^0$与每个$\\hat{\\beta}_j$都不相关,所以$u^0$与$\\hat{y}^0$不相关</p>\n<p>$$<br>Var(\\hat{e}^0)=Var(\\hat{y}^0)+Var(u^0)=Var(\\hat{y}^0)+\\sigma^2<br>$$</p>\n<p>第一项来自抽样误差,即对$\\beta_j$的估计误差</p>\n<p>$se(\\hat{e}^0)=\\sqrt{se(\\hat{y}^0)^2+\\hat{\\sigma}^2}$</p>\n<h3 id=\"残差分析\"><a href=\"#残差分析\" class=\"headerlink\" title=\"残差分析\"></a>残差分析</h3><p>计算剔除某些因素后样本的水平</p>\n<h3 id=\"因变量为-log-y-时对-y-的预测\"><a href=\"#因变量为-log-y-时对-y-的预测\" class=\"headerlink\" title=\"因变量为$\\log y$时对$y$的预测\"></a>因变量为$\\log y$时对$y$的预测</h3><p>$\\hat{y}=\\exp(\\hat{\\log y})?$ 会系统地<strong>低估</strong>$y$的预测值</p>\n<p>$\\mathbb{E}[y\\vert x]=\\exp(\\sigma^2/2)\\cdot \\exp(\\beta_0+\\beta_1x_1+\\beta_2x_2+\\dots)$</p>\n<p>$\\hat{y}=\\exp(\\hat{\\sigma}^2/2)\\exp(\\hat{\\log y})$,虽然不是无偏的,但是是一致的。它依赖于$u$的正态性</p>\n<p>一般的情况,$\\mathbb{E}[y\\vert x]=\\alpha_0\\cdot \\exp(\\beta_0+\\beta_1x_1+\\beta_2x_2+\\dots)$,$\\alpha_0$是$\\exp(u)$的期望值,且是大于一的,所以我们要求$\\hat{\\alpha}_0$</p>\n<p>矩估计$\\hat{\\alpha}_0=\\frac{1}{n}\\sum\\exp(\\hat{u}_i)$,是一个一致有偏的估计量,这是所谓的污染估计值的一种特殊形式。或者我们可以通过一个过原点的简单回归:$m_i=\\exp(\\beta_0+\\beta_1x_{i1}+\\beta_2x_{i2}+\\dots),\\mathbb{E}[y_i\\vert m_i]=\\alpha_0m_i$,这样,我们就能从$y_i$对$\\hat{m}_i$的回归中得到一个$\\alpha_0$的无偏估计:</p>\n<p>$$<br>\\tilde{\\alpha}_0=\\frac{\\sum\\hat{m}_iy_i}{\\sum\\hat{m}_i^2}<br>$$</p>\n<p><strong>拟合优度</strong></p>\n<p>在普通最小二乘中,$R^2$就是$\\hat{y}_i$与$y_i$之间的相关系数的平方,如果我们对所有观测量都计算$\\hat{y}_i=\\hat{\\alpha}_0m_i$,由于是在变量上乘了一个常数$\\hat{\\alpha}_0$,所以对$\\alpha_0$的估计不会影响到结果。我们还是计算$y<br>_i$和$\\hat{y}<br>_i$的相关系数,这样就可以在不同的因变量模型之间对比拟合优度</p>\n<h1 id=\"含有定性信息的多元回归分析:-二值(或虚拟)变量\"><a href=\"#含有定性信息的多元回归分析:-二值(或虚拟)变量\" class=\"headerlink\" title=\"含有定性信息的多元回归分析: 二值(或虚拟)变量\"></a>含有定性信息的多元回归分析: 二值(或虚拟)变量</h1><p>本部分在劳动经济学中较多涉及,不再赘述</p>\n","site":{"data":{}},"excerpt":"","more":"<head>\n <script src=\"https://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML\" type=\"text/javascript\"></script>\n <script type=\"text/x-mathjax-config\">\n MathJax.Hub.Config({\n tex2jax: {\n skipTags: ['script', 'noscript', 'style', 'textarea', 'pre'],\n inlineMath: [['$','$']]\n }\n });\n </script>\n</head>\n\n<h1 id=\"简单回归模型\"><a href=\"#简单回归模型\" class=\"headerlink\" title=\"简单回归模型\"></a>简单回归模型</h1><p>$y=\\beta_0+\\beta_1 x+u$</p>\n<p>$x$ 和$u$ 的相关性?</p>\n<p>关键假定是,$u$ 的平均值与$x$ 无关,即$\\mathbb{E}[u\\vert x]=\\mathbb{E}u$,称之为<strong>均值独立</strong></p>\n<p>$\\mathbb{E}[u\\vert x]=\\mathbb{E}u=0$ 称之为零条件均值假定,等于$0$定义了截距</p>\n<p>$\\mathbb{E}[y\\vert x]=\\beta_0+\\beta_1x$ 总体回归函数</p>\n<h2 id=\"普通最小二乘法的推导\"><a href=\"#普通最小二乘法的推导\" class=\"headerlink\" title=\"普通最小二乘法的推导\"></a>普通最小二乘法的推导</h2><p>$$<br>\\mathbb{E}[y-\\beta_1x-\\beta_0]=0\\\\\\mathbb{E}[x(y-\\beta_1x-\\beta_0)]=0<br>$$</p>\n<p>利用零条件均值假定,以及矩估计,或者使残差平方和最小,即可获得OLS一阶条件</p>\n<p>$$<br>\\begin{align*}\\sum y_i-\\hat{\\beta_0}-\\hat{\\beta_1}x_i=0\\\\\\sum x_i(y_i-\\hat{\\beta_0}-\\hat{\\beta_1}x_i)=0\\end{align*}<br>$$</p>\n<p>OLS回归线/样本回归函数:$\\hat{y}=\\hat{\\beta_0}+\\hat{\\beta_1}x$,是总体回归函数的一个样本估计,总体回归函数始终是未知的。</p>\n<h2 id=\"统计量的性质\"><a href=\"#统计量的性质\" class=\"headerlink\" title=\"统计量的性质\"></a>统计量的性质</h2><p>$\\sum \\hat{u}_i=0$, $\\sum x_i\\hat{u}_i=0$ 这其实就是一阶条件</p>\n<p>定义:</p>\n<p>总平方和SST,解释平方和SSE,残差平方和SSR</p>\n<p>$SST=\\sum(y_i-\\bar{y})^2$</p>\n<p>$SSE=\\sum (\\hat{y}_i-\\bar{y})^2$</p>\n<p>$SSR=\\sum \\hat{u}_i^2$</p>\n<p>SST=SSE+SSR</p>\n<p>拟合优度$R^2=SSE/SST$,是可解释的波动与总波动之比</p>\n<h2 id=\"OLS估计量的期望和方差\"><a href=\"#OLS估计量的期望和方差\" class=\"headerlink\" title=\"OLS估计量的期望和方差\"></a>OLS估计量的期望和方差</h2><h3 id=\"OLS的无偏性\"><a href=\"#OLS的无偏性\" class=\"headerlink\" title=\"OLS的无偏性\"></a>OLS的无偏性</h3><p><strong>SLR.1</strong> 线性与参数</p>\n<p><strong>SLR.2</strong> 随机抽样,实践过程中,并不是所有横截面样本都可以看成是随机抽样的结果</p>\n<p>$y_i=\\beta_0+\\beta_1x_i+u_i$,其中$u_i$是第$i$ 次观测的误差或干扰,与残差不同 </p>\n<p><strong>SLR.3</strong> 解释变量的样本有波动</p>\n<p>$x$ 的样本结果不是完全相同的数值</p>\n<p><strong>SLR.4</strong> 零条件均值</p>\n<p><strong>下面证明OLS的无偏性</strong></p>\n<p>$\\hat{\\beta}_1=\\frac{\\sum(x_i-\\bar{x})y_i}{\\sum(x_i-\\bar{x})^2}=\\frac{\\sum(x_i-\\bar{x})y_i}{SST_x}=\\frac{\\sum(x_i-\\bar{x})(\\beta_0+\\beta_1x_i+u_i)}{SST_x}=\\beta_1+\\frac{\\sum d_iu_i}{SST_x}$,其中$d_i=x_i-\\bar{x}$</p>\n<p>因此,$\\mathbb{E}\\hat{\\beta}_1=\\beta_1,\\mathbb{E}\\hat{\\beta}_0=\\beta_0$</p>\n<p>无偏性是抽样分布的性质,并不能确定从特定样本中得到的估计值</p>\n<p>时序分析中将会放松SLR.2</p>\n<p><strong>SLR.5</strong> 同方差性</p>\n<p>$Var(u\\vert x)=\\sigma^2$</p>\n<p>$\\sigma^2=\\mathbb{E}[u^2\\vert x]$,即$\\sigma^2$是$u$的无条件方差,也经常被成为误差方差或干扰方差</p>\n<p>若$Var(u\\vert x)$取决于$x$,则误差项表现出异方差性</p>\n<p><strong>定理 OLS估计量的抽样方差</strong></p>\n<p>在SLR.1-SLR.5条件下,对于样本值:</p>\n<p>$Var(\\hat{\\beta}_1)=\\frac{\\sigma^2}{SST_x}$</p>\n<p>$Var(\\hat{\\beta}_0)=\\frac{\\sigma^2\\bar{x}}{SST_x}+\\frac{\\sigma^2}{n}$</p>\n<p>从$\\hat{\\beta}_1=\\beta_1+\\frac{\\sum d_iu_i}{SST_x}$出发,$Var(\\hat{\\beta}_1)=\\frac{\\sum d_i^2\\sigma^2}{SST_x^2}=\\sigma^2/SST_x$</p>\n<p>一个小结论:</p>\n<p>$\\sum x_i^2\\ge\\sum(x_i-\\bar{x})^2$</p>\n<p><strong>误差方差的估计</strong></p>\n<p>$\\hat{u}_i=u_i-(\\hat{\\beta}_0-\\beta_0)-(\\hat{\\beta}_1-\\beta_1)x_i$</p>\n<p>$\\sigma^2$的一个无偏“估计量”是$\\sum u_i^2/n$ 但$u_i$不可观测</p>\n<p>OLS有两个约束条件,因此:</p>\n<p>$\\hat{\\sigma}^2=SSR/(n-2)$ 是一个无偏估计,有时记为$s^2$</p>\n<p>$$<br>0=\\bar{u}-(\\hat{\\beta}_0-\\beta_0)-(\\hat{\\beta}_1-\\beta_1)\\bar{x}\\\\\\sum\\hat{u}_i^2=\\sum(u_i-(\\hat{\\beta}_0-\\beta_0)-(\\hat{\\beta}_1-\\beta_1)x_i)^2\\\\=\\sum(u_i-\\bar{u}-(\\hat{\\beta}_1-\\beta_1)(x_i-\\bar{x}))^2<br>$$</p>\n<p>$sd(\\hat{\\beta}_1)=\\sigma/\\sqrt{SST}$它的一个比较自然的估计量就是$se(\\hat{\\beta}_1)=\\hat{\\sigma}/\\sqrt{SST}$,被称之为标准误(standard error)</p>\n<h1 id=\"多元回归分析:估计\"><a href=\"#多元回归分析:估计\" class=\"headerlink\" title=\"多元回归分析:估计\"></a>多元回归分析:估计</h1><h2 id=\"如何得到OLS估计值\"><a href=\"#如何得到OLS估计值\" class=\"headerlink\" title=\"如何得到OLS估计值\"></a>如何得到OLS估计值</h2><p>一阶条件:</p>\n<p>$$<br>\\sum(y_i-\\hat{\\beta}_0-\\hat{\\beta}_1x_{i1}-\\cdots)=0\\\\\\sum x_{i1}(y_i-\\hat{\\beta}_0-\\hat{\\beta}_1x_{i1}-\\cdots)=0\\\\\\vdots\\\\\\sum x_{ik}(y_i-\\hat{\\beta}_0-\\hat{\\beta}_1x_{i1}-\\cdots)=0<br>$$</p>\n<p>回归线或样本回归函数由截距估计值与斜率估计值组成</p>\n<p>估计值$\\hat{\\beta}_i$具有偏效应,因此多元回归使我们在对自变量的值不加限制的时候有效模拟施加限制的情况</p>\n<h2 id=\"拟合值和残差的重要性质\"><a href=\"#拟合值和残差的重要性质\" class=\"headerlink\" title=\"拟合值和残差的重要性质\"></a>拟合值和残差的重要性质</h2><ol>\n<li>残差样本平均值为零</li>\n<li>OLS拟合值和OLS残差之间的样本协方差为零</li>\n<li>样本平均在回归线上</li>\n</ol>\n<p>考虑$\\hat{y}=\\hat{\\beta}_0+\\hat{\\beta}_1x_1+\\hat{\\beta}_2x_2$,$\\hat{\\beta}_1$的一种表达形式是:$\\hat{\\beta}_1=\\frac{\\sum\\hat{r}_{i1}y_i}{\\sum\\hat{r}_{i1}^2}$</p>\n<p>其中$\\hat{r}_{i1} $是$x_1$对$x_2$的回归得到的OLS残差,即$x_{i1}$与$x_{i2}$中不相关的部分,所以$\\hat{\\beta}_1$就是排除了$x_2$影响后$y$与$x_1$之间的关系</p>\n<h3 id=\"简单回归与多元回归\"><a href=\"#简单回归与多元回归\" class=\"headerlink\" title=\"简单回归与多元回归\"></a>简单回归与多元回归</h3><p>$\\tilde{y}=\\tilde{\\beta}_0+\\tilde{\\beta}_1x_1$和$\\hat{y}=\\hat{\\beta}_0+\\hat{\\beta}_1x_1+\\hat{\\beta}_2x_2$的结果会有什么关系?</p>\n<p>令$\\bar{\\delta}$是$x_2$对$x_1$的简单回归斜率,则$\\tilde{\\beta}_1=\\hat{\\beta}_1+\\hat{\\beta}_2\\bar{\\delta}$</p>\n<p><strong>拟合优度相关的内容和简单线性回归一致</strong></p>\n<p>增加一个自变量之后$R^2$不会减小,而且通常会增大</p>\n<h2 id=\"OLS估计量的期望\"><a href=\"#OLS估计量的期望\" class=\"headerlink\" title=\"OLS估计量的期望\"></a>OLS估计量的期望</h2><p><strong>MLR.1</strong> 线性于参数</p>\n<p><strong>MLR.2</strong> 随机抽样</p>\n<p><strong>MLR.3</strong> 不存在完全共线性</p>\n<p><strong>MLR.4</strong> 条件均值为零</p>\n<p>当MLR.4成立时,我们说具有外生解释变量,如果$x_j$与$u$相关,那么$x_j$称之为内生解释变量</p>\n<p>限制了无法观测的因素与解释变量之间的关系</p>\n<p>在MLR1-4条件下,可以证明OLS的无偏性$\\mathbb{E}\\hat{\\beta}_i=\\beta_i$</p>\n<p>包含无关变量一般不会对OLS的无偏性产生影响,但是会对方差产生不利影响</p>\n<p><strong>遗漏变量偏误</strong></p>\n<p>总体模型:$y=\\beta_0+\\beta_1x_1+\\beta_2x_2+\\beta_3x_3+u$</p>\n<p>遗漏变量后的估计模型:$\\tilde{y}=\\tilde{\\beta}_0+\\tilde{\\beta}_1x_1+\\tilde{\\beta}_2x_2$</p>\n<p><strong>假设$x_2$和$x_3$无关,$x_1$和$x_3$相关</strong></p>\n<p>$$<br>\\mathbb{E}\\tilde{\\beta}_1=\\beta_1+\\beta_3\\frac{\\sum x_{i3}(x_{i1}-\\bar{x}_1)}{\\sum (x_{i1}-\\bar{x}_1)^2}<br>$$</p>\n<p><strong>MLR.5</strong> 同方差性 $Var[u\\vert x_1,x_2,\\dots,x_k]=\\sigma^2$</p>\n<p>即以解释变量为条件,不管解释变量出现怎样的组合,误差项的方差都是一样的。如果不成立称之为异方差性</p>\n<p>MLR1-5称之为横截面回归的<strong>高斯-马尔可夫</strong>假定</p>\n<p>$Var\\hat{\\beta}_i=\\frac{\\sigma^2}{SST_j(1-R_j^2)}$,其中$R_j$来自于$x_j$对其他变量回归得到的$R^2$,需要MLR.5的的成立</p>\n<p>两个或多个自变量之间高度但不完全相关称之为<strong>多重共线性</strong>,即$R_j^2$接近于1,但这并不违反MLR.3,最终的问题还是要看$\\hat{\\beta}_j$与自身的标准差的大小关系</p>\n<p>很小的$SST_j$也可以导致大方差,即小样本容量会导致很大的抽样方差</p>\n<p>如果存在相关性的自变量和我们关注的自变量没有高度相关,其实没有直接影响,就不必关心这种共线性</p>\n<p>误设模型中的方差</p>\n<p>$Var\\hat{\\beta}_i=\\frac{\\sigma^2}{SST_j(1-R_j^2)}$,和$Var\\tilde{\\beta}_i=\\frac{\\sigma^2}{SST_j}$</p>\n<p>若$\\beta_2\\neq0$,则简单模型给出方差更小的有偏估计;若$\\beta_2=0$,则简单模型给出方差更小的无偏估计。</p>\n<p>直觉上讲,如果$x_2$对$y$没有偏效应,在回归中加入$x_2$只会加剧多重共线性。如果$\\beta_2\\neq0$,则偏误不会随着样本容量扩大而减小,但是Var会随着样本容量增大而趋于零,因此增加自变量导致的多重共线性就会变得没那么重要,大样本情况下倾向使用更复杂的模型</p>\n<h3 id=\"OLS估计的标准误\"><a href=\"#OLS估计的标准误\" class=\"headerlink\" title=\"OLS估计的标准误\"></a>OLS估计的标准误</h3><p>$$<br>\\hat{\\sigma}^2=\\frac{\\sum u_i^2}{n-k-1}=\\frac{SSR}{n-k-1}<br>$$</p>\n<p>自由度$df=n-k-1$</p>\n<p>可以证明,$\\mathbb{E}\\hat{\\sigma}^2=\\sigma^2$</p>\n<p>$\\hat{\\sigma}=\\sqrt{\\hat{\\sigma}^2}$称之为回归标准误SER,是误差项的标准差的估计量,还被称之为估计值标准误和均方误差</p>\n<p>$se(\\hat{\\beta}_i)=\\frac{\\hat{\\sigma}^2}{\\sqrt{SST_j(1-R_j)^2}}$</p>\n<p>异方差性质不会导致参数估计偏误,但是会导致$Var(\\hat{\\beta}_j)$出现问题,导致标准误无效</p>\n<h2 id=\"OLS的有效性\"><a href=\"#OLS的有效性\" class=\"headerlink\" title=\"OLS的有效性\"></a>OLS的有效性</h2><p>在MLR1-5的假定下,OKS估计量是最优线性无偏估计量BLUE,即具有最小的方差。尤其是MLR.5,保证了OLS在线性无偏估计量中具有最小的方差</p>\n<h1 id=\"多元回归分析:推断\"><a href=\"#多元回归分析:推断\" class=\"headerlink\" title=\"多元回归分析:推断\"></a>多元回归分析:推断</h1><h2 id=\"OLS估计量的抽样分布\"><a href=\"#OLS估计量的抽样分布\" class=\"headerlink\" title=\"OLS估计量的抽样分布\"></a>OLS估计量的抽样分布</h2><p><strong>MLR.6</strong> 正态性 总体误差$u$独立于解释变量,并且服从均值为零,方差为$\\sigma^2$的正态分布</p>\n<p>MLR1-6称之为经典线性模型(CLM)假定。在CLM下,OLS是最小方差的无偏估计,不必限制在线性估计中</p>\n<p>由千于$u$ 是影响着 $y$ 而又观测不到的许多因素之和,所以我们可借助中心极限定理断定 $u$ 具有近似正态分布</p>\n<p>通常我们可以利用某种变换得到一个$u$接近于正态的分布</p>\n<p>误差项的正态性导致了OLS估计量的正态抽样分布</p>\n<p>$$<br>\\frac{\\hat{\\beta}_j-\\beta_j}{sd(\\hat{\\beta}_j)}\\sim Normal(0,1)<br>$$</p>\n<h2 id=\"对单个总体参数的检验:t检验\"><a href=\"#对单个总体参数的检验:t检验\" class=\"headerlink\" title=\"对单个总体参数的检验:t检验\"></a>对单个总体参数的检验:t检验</h2><p>在CLM假定下,$\\frac{\\hat{\\beta}_j-\\beta_j}{se(\\hat{\\beta}_j)}\\sim t_{n-k-1}$</p>\n<p>多数应用中,主要兴趣在于检验原假设$H_0:\\beta_j=0$</p>\n<p>为什么不反过来写?因为$x_j$对$y$有偏效应的表述对$\\beta_j$不为零对任何一个值都成立</p>\n<p>$t_{\\hat{\\beta}_j}=\\hat{\\beta}_j/se(\\hat{\\beta}_j)$称之为t统计量</p>\n<p><strong>单侧/双侧备择假设,t检验p值 ,置信区间</strong></p>\n<p>参考概统知识,此处不表</p>\n<h2 id=\"检验关于参数的一个线性组合假设\"><a href=\"#检验关于参数的一个线性组合假设\" class=\"headerlink\" title=\"检验关于参数的一个线性组合假设\"></a>检验关于参数的一个线性组合假设</h2><p>$H_0:\\beta_1=\\beta_2$ 如何检验?</p>\n<p>$t=\\frac{\\hat{\\beta}_1-\\hat{\\beta}_2}{se(\\hat{\\beta}_1-\\hat{\\beta}_2)}$,关键是求解标准误,即要求解$Cov(\\hat{\\beta}_1,\\hat{\\beta}_2)$的一个估计值,这在数学上是复杂的</p>\n<p>但我们可以改写模型$\\beta_1=\\theta_1+\\beta_2$</p>\n<p>$y=\\beta_0+(\\theta_1+\\beta_2)x_1+\\beta_2x_2+u=\\beta_0+\\theta_1x_1+\\beta_2(x_1+x_2)+u$</p>\n<p>直接检验$\\theta_1$即可</p>\n<h2 id=\"对多个线性约束对检验:F检验\"><a href=\"#对多个线性约束对检验:F检验\" class=\"headerlink\" title=\"对多个线性约束对检验:F检验\"></a>对多个线性约束对检验:F检验</h2><p>原假设:$H_0:\\beta_{k-q+1}=0,\\dots\\beta_k=0$</p>\n<p>不含$\\beta_{\\dots}$的模型是受约束模型,原始模型称之为不受约束模型</p>\n<p>受约束模型增加了$q$个排除性约束,定义$F$统计量</p>\n<p>$$<br>F=\\frac{(SSR_r-SSR_{ur})/q}{SSR_{ur}/(n-k-1)}=\\frac{(R_{ur}^2-R_r^2)/q}{(1-R_{ur}^2)/df_{ur}}\\sim F_{q,n-k-1}<br>$$</p>\n<p>其中$SSR_r$是受约束模型的残差平方和,$SSR_{ur}$是不受约束的残差平方和,$q=df_r-df_{ur}$</p>\n<p>如果拒绝原假设,那么就说$x_{k-q+1},\\dots x_k$ 在适当的显著性水平上是联合统计显著的</p>\n<p><strong>对于一般的线性约束</strong></p>\n<p>如指定了$\\beta_1=1$,则将$x_1$挪到回归方程左边</p>\n<p>由于两次的因变量不同,不能采用$R^2$形式的统计量</p>\n<h1 id=\"多元回归分析:OLS的渐进性\"><a href=\"#多元回归分析:OLS的渐进性\" class=\"headerlink\" title=\"多元回归分析:OLS的渐进性\"></a>多元回归分析:OLS的渐进性</h1><h2 id=\"一致性\"><a href=\"#一致性\" class=\"headerlink\" title=\"一致性\"></a>一致性</h2><p>直观的理解:当样本量趋于无穷时,收敛到真值</p>\n<p><strong>Theory OLS</strong>的一致性</p>\n<p>在MLR1-4下,$\\hat{\\beta}_j$是$\\hat{\\beta}_j$的一致估计</p>\n<p><em>PROOF</em></p>\n<p>$$<br>X\\beta+u=y\\\\\\hat{\\beta}=(X^TX)^{-1}X^Ty=(X^TX)^{-1}X^T(X\\beta+u)\\\\=\\beta+(X^TX)^{-1}X^Tu=\\beta+(\\frac{1}{n}\\sum_{i=1}^n x_i^Tx_i)^{-1}(\\frac{1}{n}\\sum _{i=1}^nx_i^Tu)<br>$$</p>\n<p>according to the large number law:</p>\n<p>$$<br>\\frac{1}{n}\\sum x_i^Tx_i\\xrightarrow{p}\\mathbb{E}x_i^Tx_i=A,\\quad \\frac{1}{n}\\sum x_i^T u\\xrightarrow{p}\\mathbb{E}x_iu=0<br>$$</p>\n<p>because $A$ is a nonsingular matrix, so$(\\frac{1}{n}\\sum x_i^Tx_i)^{-1}\\xrightarrow{p}A^{-1}$</p>\n<p>$$<br>plim \\hat{\\beta}=\\beta+A^{-1}\\cdot0=\\beta<br>$$</p>\n<p><strong>假设MLR.4’ 零均值和零相关</strong></p>\n<p>对所有的$j$,都有$\\mathbb{E}u=0$和$Cov(x_j,u)=0$</p>\n<p>这是一个比MLR.4更弱的假定,它只要求每个$x_j$与$u$无关。</p>\n<p>这导致$x_j$的非线性函数可能与误差相关</p>\n<p><strong>OLS的不一致性</strong></p>\n<p>如果误差与任何一个自变量相关,那么OLS就是有偏而不一致的估计。随着样本容量的增大,偏误将持续存在。</p>\n<p>$$<br>plim \\hat{\\beta_1}-\\beta_1=\\frac{Cov(x_1,u)}{Var(x_1)}<br>$$</p>\n<p>不一致性用总体的性质表示,而偏误则基于样本的对应量表示</p>\n<h2 id=\"渐近正态和大样本推断\"><a href=\"#渐近正态和大样本推断\" class=\"headerlink\" title=\"渐近正态和大样本推断\"></a>渐近正态和大样本推断</h2><p><strong>Theory</strong> OLS的渐进正态性</p>\n<p>在MLR1-5下,</p>\n<p>1.<br>$\\sqrt{n}(\\hat{\\beta}_j-\\beta_j)\\xrightarrow x N(0,\\sigma^2/a_j^2),a_j^2=plim(n^{-1}\\sum_{i=1}^n \\hat{r_{ij}}^2)$,其中$\\hat{r}_{ij}$是$x_j$对其余自变量回归得到的残差,即不能被其他变量解释的部分,我们称$\\hat{\\beta}_j$是渐进正态分布的<br>2. $\\hat{\\sigma}^2$是$\\sigma^2=Var(u)$的一个一致估计<br>3. 对于每个$j$都有$(\\hat{\\beta}_j-\\beta_j)/sd(\\hat{\\beta}_j)\\xrightarrow x N(0,1)$,且$(\\hat{\\beta}_j-\\beta_j)/se(\\hat{\\beta}_j)\\xrightarrow x N(0,1)$</p>\n<p>去掉了MLR.6,只需要有限方差且零均值与同方差性质</p>\n<p>总体分布恒定,与样本数量大小没有关系</p>\n<p>$\\hat{\\beta}_j$的估计方差:$\\hat{Var(\\hat{\\beta}_j)}=\\frac{\\hat{\\sigma}^2}{SST_j(1-R_j^2)}$,以$1/n$的速度收缩至零</p>\n<h3 id=\"拉格朗日乘数LM统计量\"><a href=\"#拉格朗日乘数LM统计量\" class=\"headerlink\" title=\"拉格朗日乘数LM统计量\"></a>拉格朗日乘数LM统计量</h3><ol>\n<li>将$y$对施加限制后的自变量集回归,保存残差$\\tilde{u}$</li>\n<li>将$\\tilde{u}$对所有自变量进行回归,得到$R_u^2$</li>\n<li>计算$LM=nR_u^2$</li>\n<li>将LM与$\\chi_q^2$分布中适当的临界值$c$比较,如果$LM>c$,则拒绝原假设,说明后$q$个变量的系数不为零</li>\n</ol>\n<h2 id=\"OLS的渐近有效性\"><a href=\"#OLS的渐近有效性\" class=\"headerlink\" title=\"OLS的渐近有效性\"></a>OLS的渐近有效性</h2><p>在模型$y=\\beta_0+\\beta_1x_1+u$中,在MLR.4假设下,$\\mathbb{E}[u\\vert x]=0$,我们关注斜率</p>\n<p>令$z_i=g(x_i)$,$g$为任意函数,那么$u$就与$g(x)$无关。假定$Cov(z,x)\\neq 0$,那么,估计量</p>\n<p>$$<br>\\tilde{\\beta}_1=\\sum(z_i-\\bar{z})y_i/\\sum (z_i-\\bar{z})x_i<br>$$</p>\n<p>是对$\\beta_1$的一致估计。(证明:在分子分母分别除n并使用大数定律)</p>\n<p>$$<br>plim \\tilde{\\beta_1}=\\beta_1+Cov(z,u)/Cov(z,x)=\\beta_1<br>$$</p>\n<p><strong>Theory</strong> OlS的渐近有效性</p>\n<p>高斯-马尔可夫假设下,OLS估计量具有最小的渐近方差,</p>\n<p>$$<br>Avar \\sqrt{n}(\\hat{\\beta}_j-\\beta_j)\\le Avar\\sqrt{n}(\\tilde{\\beta}_j-\\beta_j)<br>$$</p>\n<h1 id=\"深入专题\"><a href=\"#深入专题\" class=\"headerlink\" title=\"深入专题\"></a>深入专题</h1><h2 id=\"数据测度单位对-OLS-统计量的影晌\"><a href=\"#数据测度单位对-OLS-统计量的影晌\" class=\"headerlink\" title=\"数据测度单位对 OLS 统计量的影晌\"></a>数据测度单位对 OLS 统计量的影晌</h2><p>度量单位对系数、标准误、置信区间、t统计量、F统计量的影响不会影响结果。</p>\n<p><strong>$\\beta$系数</strong></p>\n<p>将所有变量都标准化后的回归结果得到的系数称为标准化系数或$\\beta$系数 $\\hat{b}_j=(\\delta_j/\\delta_y)\\hat{\\beta}_j$</p>\n<p>由此得到的$\\beta$系数大小更具有说服力</p>\n<h2 id=\"函数形式的进一步讨论\"><a href=\"#函数形式的进一步讨论\" class=\"headerlink\" title=\"函数形式的进一步讨论\"></a>函数形式的进一步讨论</h2><h3 id=\"对数函数\"><a href=\"#对数函数\" class=\"headerlink\" title=\"对数函数\"></a>对数函数</h3><p>$\\log(y)=\\hat{\\beta}_0+\\hat{\\beta}_1\\log x_1+\\hat{\\beta}_2x_2$</p>\n<p>固定$x_1$不变,有$\\Delta \\hat{\\log y}=\\hat{\\beta}_2 \\Delta x_2$,即$%\\Delta\\hat{y}=100\\cdot[\\exp(\\hat{\\beta}_2\\Delta x_2)-1]$是精确的预测变化百分比,它是一致的,但却不是无偏的,因为指数函数的非线性</p>\n<p><strong>对数的好处:</strong></p>\n<ol>\n<li>斜率系数不随测度单位而变化,所以我们可以忽略以对数形式出现的变量的度量单位</li>\n<li>严格为正的变量,条件分布常常具有异方差性或偏态性,取对数后可以降低</li>\n<li>对数通常可以缩小变量的取值范围,对极端值也没有那么敏感</li>\n</ol>\n<p><strong>问题:</strong></p>\n<ol>\n<li>变量在0、1之间时,会导致变换后的数据绝对值很大</li>\n<li>更加难以预测原变量的值。两者的$R^2$也不具有可比性</li>\n</ol>\n<h3 id=\"含二次式的模型\"><a href=\"#含二次式的模型\" class=\"headerlink\" title=\"含二次式的模型\"></a>含二次式的模型</h3><p>一次项导致的变化表达式要重写,和变量本身也有关</p>\n<h3 id=\"含有交互项的模型\"><a href=\"#含有交互项的模型\" class=\"headerlink\" title=\"含有交互项的模型\"></a>含有交互项的模型</h3><p>$y=\\beta_0+\\beta_1x_1+\\beta_2x_2+\\beta_3x_1x_2+u$$y=\\beta_0+\\beta_1x_1+\\beta_2x_2+\\beta_2x_1x_2+u$</p>\n<p>此时$\\beta_2$是$x_1=0$时$x_2$对$y$的偏效应,没什么意义</p>\n<p>$y=\\beta_0+\\beta_1x_1+\\beta_2x_2+\\beta_3(x_1-\\mu_1)(x_2-\\mu_2)+u$</p>\n<p>这样就是在均值处的偏效应了</p>\n<h2 id=\"拟合优度和回归元选择的进一步探讨\"><a href=\"#拟合优度和回归元选择的进一步探讨\" class=\"headerlink\" title=\"拟合优度和回归元选择的进一步探讨\"></a>拟合优度和回归元选择的进一步探讨</h2><p>较小的$R^2$意味着误差方差相对$y$的方差太大了,以及我们很难精确地估计$\\beta_j$,但大样本容量可以抵消较大的误差方差。</p>\n<h3 id=\"调整-R-2\"><a href=\"#调整-R-2\" class=\"headerlink\" title=\"调整$R^2$\"></a>调整$R^2$</h3><p>$R^2=1-\\frac{SSR/n}{SST/n}$</p>\n<p>总体$R^2$定义为$1-\\sigma_u^2/\\sigma_y^2$,这是$y$的变化在总体中可以用自变量解释的部分比例,是我们希望用$R^2$估计的值</p>\n<p>但是用$SSR/n$估计$\\sigma_u^2$是有偏的,用$\\hat{\\sigma}^2=SSR/(n-k-1)$显然更好,同理,用$SST/(n-1)$代替$SST/n$</p>\n<p>由此,得到调整$R^2$:</p>\n<p>$\\bar{R^2}=1-\\hat{\\sigma}^2/[SST/(n-1)]=1-(1-R^2)\\frac{n-1}{n-k-1}$</p>\n<p>虽然两个无偏估计的比不是无偏估计,但是$\\bar{R^2}$在模型中额外增加自变量时施加了惩罚,在回归中增加一个变量时,只有新变量的t统计量大于1,$\\bar{R^2}$才会提高,增加一组变量时,联合检验显著的F统计量大于1才会提高</p>\n<h3 id=\"利用调整-R-2-在两个非嵌套模型-nonnested-中进行选择\"><a href=\"#利用调整-R-2-在两个非嵌套模型-nonnested-中进行选择\" class=\"headerlink\" title=\"利用调整$R^2$在两个非嵌套模型 (nonnested) 中进行选择\"></a>利用调整$R^2$在两个非嵌套模型 (nonnested) 中进行选择</h3><p>Definition: 两个方程没有哪一个是另一个的特殊情形,所以它们是非嵌套模型</p>\n<p>在这种情况下,使用普通$R^2$对自变量较少的模型不公平</p>\n<p>当自变量组对应着不同的函数形式时,调整$R^2$也是有价值的</p>\n<p>遗憾的是,<strong>不能</strong>通过拟合优度决定不同的因变量形式,因为它们的总变化是不同的,拟合的是两个完全不同的因变量</p>\n<p><strong>回归分析中控制过多的因素</strong></p>\n<p>注重对回归做其他条件不变的解释即可</p>\n<p><strong>增加回归元以减少误差方差</strong></p>\n<p>增加适当的无关变量可以减小误差方差,在大样本容量的情况下,所有OLS估计量对标准误都会减小</p>\n<h2 id=\"预测和残差分析\"><a href=\"#预测和残差分析\" class=\"headerlink\" title=\"预测和残差分析\"></a>预测和残差分析</h2><h3 id=\"预测的置信区间\"><a href=\"#预测的置信区间\" class=\"headerlink\" title=\"预测的置信区间\"></a>预测的置信区间</h3><p>估计方程:$\\hat{y}=\\hat{\\beta}_0+\\hat{\\beta}_1x_1+\\hat{\\beta}_2x_2+\\dots$</p>\n<p>$\\theta_0=\\beta_0+\\beta_1c_1+\\beta_2c_2+\\dots$ 的估计量是:</p>\n<p>$\\hat{\\theta}_0=\\hat{\\beta}_0+\\hat{\\beta}_1c_1+\\hat{\\beta}_2c_2+\\dots$ 我们关注它的置信区间</p>\n<p>在$df$较大的情况下,我们可以利用经验法则$\\hat{\\theta}_0\\pm2\\cdot se(\\hat{\\theta}_0)$构造95%置信区间</p>\n<p>求$se(\\hat{\\theta}_0)$:</p>\n<p>$\\theta_0$表达式代入方程:$y=\\theta_0+\\beta_1(x_1-c_1)+\\beta_2(x_2-c_2)+\\dots$</p>\n<p>用样本回归一下就可以了,截距项是预测值,还可以得到标准误</p>\n<p>由于每个解释变量的样本均值都为零时,截距估计量的方差最小,所以当$x_j$都取均值时,预测值的方差最小。随着$c_j$的值离中心越来越远,误差越来越大</p>\n<p>令$y^0$表示我们构造一个置信区间(预测区间)的估计值</p>\n<p>$$<br>\\hat{y}^0=\\hat{\\beta}_0+\\hat{\\beta}_1x_1^0+\\cdots+\\\\\\hat{e}^0=y^0-\\hat{y}^0=\\beta_0+\\beta_1x_1^0+\\cdots+u^0-\\hat{y}^0\\\\\\mathbb{E}\\hat{e}^0=0<br>$$</p>\n<p>所以预测误差的期望值为零</p>\n<p>$u^0$与用来得到$\\hat{\\beta}_j$的样本方差不相关,$u^0$与每个$\\hat{\\beta}_j$都不相关,所以$u^0$与$\\hat{y}^0$不相关</p>\n<p>$$<br>Var(\\hat{e}^0)=Var(\\hat{y}^0)+Var(u^0)=Var(\\hat{y}^0)+\\sigma^2<br>$$</p>\n<p>第一项来自抽样误差,即对$\\beta_j$的估计误差</p>\n<p>$se(\\hat{e}^0)=\\sqrt{se(\\hat{y}^0)^2+\\hat{\\sigma}^2}$</p>\n<h3 id=\"残差分析\"><a href=\"#残差分析\" class=\"headerlink\" title=\"残差分析\"></a>残差分析</h3><p>计算剔除某些因素后样本的水平</p>\n<h3 id=\"因变量为-log-y-时对-y-的预测\"><a href=\"#因变量为-log-y-时对-y-的预测\" class=\"headerlink\" title=\"因变量为$\\log y$时对$y$的预测\"></a>因变量为$\\log y$时对$y$的预测</h3><p>$\\hat{y}=\\exp(\\hat{\\log y})?$ 会系统地<strong>低估</strong>$y$的预测值</p>\n<p>$\\mathbb{E}[y\\vert x]=\\exp(\\sigma^2/2)\\cdot \\exp(\\beta_0+\\beta_1x_1+\\beta_2x_2+\\dots)$</p>\n<p>$\\hat{y}=\\exp(\\hat{\\sigma}^2/2)\\exp(\\hat{\\log y})$,虽然不是无偏的,但是是一致的。它依赖于$u$的正态性</p>\n<p>一般的情况,$\\mathbb{E}[y\\vert x]=\\alpha_0\\cdot \\exp(\\beta_0+\\beta_1x_1+\\beta_2x_2+\\dots)$,$\\alpha_0$是$\\exp(u)$的期望值,且是大于一的,所以我们要求$\\hat{\\alpha}_0$</p>\n<p>矩估计$\\hat{\\alpha}_0=\\frac{1}{n}\\sum\\exp(\\hat{u}_i)$,是一个一致有偏的估计量,这是所谓的污染估计值的一种特殊形式。或者我们可以通过一个过原点的简单回归:$m_i=\\exp(\\beta_0+\\beta_1x_{i1}+\\beta_2x_{i2}+\\dots),\\mathbb{E}[y_i\\vert m_i]=\\alpha_0m_i$,这样,我们就能从$y_i$对$\\hat{m}_i$的回归中得到一个$\\alpha_0$的无偏估计:</p>\n<p>$$<br>\\tilde{\\alpha}_0=\\frac{\\sum\\hat{m}_iy_i}{\\sum\\hat{m}_i^2}<br>$$</p>\n<p><strong>拟合优度</strong></p>\n<p>在普通最小二乘中,$R^2$就是$\\hat{y}_i$与$y_i$之间的相关系数的平方,如果我们对所有观测量都计算$\\hat{y}_i=\\hat{\\alpha}_0m_i$,由于是在变量上乘了一个常数$\\hat{\\alpha}_0$,所以对$\\alpha_0$的估计不会影响到结果。我们还是计算$y<br>_i$和$\\hat{y}<br>_i$的相关系数,这样就可以在不同的因变量模型之间对比拟合优度</p>\n<h1 id=\"含有定性信息的多元回归分析:-二值(或虚拟)变量\"><a href=\"#含有定性信息的多元回归分析:-二值(或虚拟)变量\" class=\"headerlink\" title=\"含有定性信息的多元回归分析: 二值(或虚拟)变量\"></a>含有定性信息的多元回归分析: 二值(或虚拟)变量</h1><p>本部分在劳动经济学中较多涉及,不再赘述</p>\n"},{"layout":"posts","title":"Managing cash-in risk embedded in Portfolio Insurance strategies","date":"2022-04-17T16:00:00.000Z","_content":"\n<head>\n <script src=\"https://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML\" type=\"text/javascript\"></script>\n <script type=\"text/x-mathjax-config\">\n MathJax.Hub.Config({\n tex2jax: {\n skipTags: ['script', 'noscript', 'style', 'textarea', 'pre'],\n inlineMath: [['$','$']]\n }\n });\n </script>\n</head>\n\n# Managing cash-in risk embedded in Portfolio\nInsurance strategies: a review\n\nthe presence of an insurance could have convinced the investors to not leave the market, and **take risk**\n\nPerold and Sharpe: 3 different insurance strategies: option-based \\ option-duplicating \\ derivative independent \n\noption-based: buy zero-coupon bond maturity equals investment time horizon + risky option\n\noption-duplicating: replicate option with a self-financing strategy (overcome the lack of liquidity)\n\nlow interest rate level reduce the available risk budgets. both a sustainable equity & capital protection? **dynamically allocating both in risky and riskless assets** mostly used—CPPI\n\n**the problem of CPPI:**\n\nafter a severe market draw-down, the risk budget **erases** — cash-in risk\n\n1. the remaining portfolio value shifted into the riskless asset, might not guarantee\n2. subsequent rises of the risky asset\n\n# OBPI\n\nkey: ensuring a minimal terminal portfolio value\n\n$V_t^{OBPI}=qB_t+pC(t,S_t,K)$\n\nthe strategy is static, no trading occurs in $(0,T)$\n\nif the option whose strike price equal to the wealth to be immunized are not traded on the market, investors must replicate the option using hedge strategies. But the incompleteness...\n\n# CPPI\n\nthe value of the portfolio at maturity $V_T^{CPPI}$ is higher than a guaranteed amount $G$ a proportion (PL) of the initially invested amount $V_0^{CPPI}$\n\nfloor $F_t=F_T(1+r)^{-(T-t)},F_T=G$\n\n*cushion $C_t$*, the difference between $V_t$ and $F_t$. exposure to risky asset $E_t=m\\times C_t$, $m$ is the multiplier. the strategy is self-financed, so the rest of the portfolio $V_t-E_t$ is invested into risk-free asset.\n\nto avoid excessive equity exposure, $E_t$ is bounded to be at most $LEV\\cdot V_t^{CPPI}$\n\nthe proportion of wealth invested to the risky asset:\n\n$$\n\\alpha_t^{CPPI}=\\min\\{\\frac{m(V_t^{CPPI}-F_t)}{V_t^{CPPI}},LEV\\}\\\\\\\\\\beta_t=1-\\alpha_t\n$$\n\n## CPPI with continuous rebalancing\n\nfloor process $F=\\{F_t\\}_{t\\in[0,T]}$, the dynamic is $dF_t=rF_tdt,F_0=G\\cdot e^{-rT}$, $W_t$ is a standard Brownian motion in real world measure $\\mathbb{P}$\n\n$$\ndV_t=mC_t\\frac{dS_t}{S_t}+(V_t-mC_t)rdt\\\\\\dS_t=r S_tdt+\\sigma S_tdW_t^\\mathbb{P}\\\\\\\\\\frac{dC_t}{C_t}=((1-m)r+\\mu m)dt+m\\sigma dW_t^\\mathbb{P}\\\\\\C_t=C_0\\exp(rt+m(\\mu-r)t+m\\sigma W_t^\\mathbb{P}-\\frac{m^2\\sigma^2t}{2})\\\\\\\\=C_0\\exp(r(1-m)t+\\frac{m(1-m)\\sigma^2t}{2})(\\frac{S_t}{S_0})^m\\\\\\V_0=C_0+F_0\\to C_0=G/PL-Ge^{-rT}\\\\\\V_T=C_T+G=G+\\frac{G}{PL}(1-PLe^{-rT})\\exp((rT+\\frac{m\\sigma^2T}{2})(1-m))(\\frac{S_T}{S_0})^m\n$$\n\nthe CPPI strategy is equivalent to taking a long position in a zero-coupon bond with nominal $G$ to guarantee the capital at maturity and investing the remaining sum into a risky asset which has $m$ times the excess return and $m$ times the volatility of $S$ and is perfectly correlated with $S$.\n\nthere is non zero probability that during a sudden downside movement of the underlying asset, the fund manager will have no time to readjust the portfolio. then it goes crashing through the floor.\n\n## CPPI with discrete time rebalancing\n\ndiscrete time CPPI:\n\n$$\n\\tau=\\{t_0=0<t_1<\\cdots<t_{n-1}=T\\}\\\\\\C_{t_{k+1}}^\\tau=C_{t_0}^\\tau\\prod_{i=1}^{min(\\nu,k+1)}(m\\frac{S_{t_i}}{S_{t_{i-1}}}-(m-1))\\\\\\nu:=min(t_k\\in\\tau\\vert V_{t_K}^\\tau-G),\\infty \\text{if not attained}\\\\\\phi_t^{(S),\\tau}:=max(\\frac{mC_{t_k}^\\tau}{S_{t_k}},0)\n$$\n\nlocal shortfall probability\n\nshortfall probability\n\nexpected shortfall\n\nhow to ensure the effectiveness of CPPI strategy?\n\n1. given an estimate for $\\mu$ and $\\sigma$, determine the value of multiplier and the number of rebalances $n$ to let the probability of falling below the guarantee above a confidence level\n2. base on large deviations methods, estimate the possible losses between two consecutive trading dates\n\n## CPPI in presence of jump in asset price\n\nno relax on continuous trading assumptions, we introduce jumps in the risky asset\n\nthe cash-in risk cannot be attributed exclusively to trading restriction\n\n$$\ndB_t=rB_tdt,B_0=b\\\\\\\\dS_t=S_{t-}dZ_t\n$$\n\n$Z$ is a possible discontinuous driving process, modeled as semi-martingale, to ensure the positivity of the price, we assume that $\\Delta Z_t>-1$, and $\\nu=\\inf(t\\ge 0,V_t\\le F_t)$, when $t<\\nu$:\n\n$$\ndV_t=m(V_{t-}-F_t)\\frac{dS_t-}{S_{t-}}+(V_{t-}-m(V_{t-}-F_t))\\frac{dB_t}{B_t}\\\\\\frac{dC_t}{C_t-}=mdZ_t+(1-m)rdt\n$$\n\nintroduce the discounted cushion $C_t^*=C_t/B_t$\n\n$$\n\\frac{dC_t^*}{C_{t-}^*}=m(dZ_t-rdt)=mdL_t,L_t=L_0+\\int_0^tdZ_s-rds\\\\\\\\C_t^*=C_0\\mathcal{E}(mL)_t\n$$\n\nat time $\\nu$, all the portfolio is invested into risk-free asset and when $t\\ge \\nu$, the value of $C_t^*$ remains constant. Define $\\tilde{C}\\_t=C_{t\\wedge\\nu}^*=C\\_0^*\\mathcal{E}(mL)\\_{t\\wedge \\nu}$\n\nit can become negative in presence of negative jumps of sufficient size of stock price.\n\n# Some extensions of CPPI allocation strategy\n\n## Time-Invariant Portfolio Protection (TIPP)\n\nmodifies the floor:\n\n$$\n\\tilde{F}\\_t=max(F\\_t,PL\\cdot \\sup_{s\\le t} V\\_s)\n$$\n\n$PL$ is the protection level. the floor will jump up with the portfolio value in order to reduce the risky asset allocation when the market peaks\n\nthe growth rate of the TIPP floor can be considered comparable to the portfolio in each instant of time\n\nless exposure to the risky asset, change more smoothly over time, the overall return will be generally lower\n\n## Variable Proportion Portfolio Insurance (VPPI)\n\nmake the multiplier dynamic\n\nEPPI: the multiplier changes like this:\n\nat $t=0$ the investor fix a reference price for the risky asset rebalancing $S^{(0)}$,\n\n$$\nm_t=\\eta+\\exp(aln(\\frac{S^{(1)}}{S^{(0)}}))\n$$\n\n$\\eta>1$ is an arbitrary constant, and the rest is the dynamic multiple adjustment factor (DMAF)\n\nwhen the stock price goes up, the mechanism of the EPPI strategy creates more number of holding shares to perform an upside capture\n\nfix the multiplier at each rebalancing date by considering a local quantile guarantee condition posed by $\\mathbb{P}\\_{t\\_k}(C\\_{t\\_{K+1}}>0\\vert C\\_{t\\_k}>0)=\\\\\\\\\\mathbb{P}\\_{t\\_k}(m\\_{t\\_k}\\frac{S\\_{t\\_{k+1}}}{S\\_{t\\_k}}-(m\\_{t\\_k}-1)>0)\\ge 1-\\epsilon$\n\nit implies an upper bound $\\bar{m}_{t_k}$, the precise number is determined by the distribution\n\n# Hedging gap risk embedded through options\n\nanother way to hedge gap risk embedded in portfolio insurance strategies is to use **options**\n\ntake a long position on an at-the-money put option on the CPPI portfolio with a strike price at least equal to the minimum value that the investor requires at maturity\n\nor take a long position on an at-the-money call option on the CPPI portfolio\n\nkey: model option on CPPI\n\n## Modeling option on CPPI\n\nthe discrete time process describing the evolution of the risky asset under the risk neutral probability measure $\\mathbb{Q}$ is:\n\n$$\n\\frac{S\n\\_{t\\_k}}{S\\_{t\\_{k+1}}}=\\exp((r-\\frac{\\sigma}{2})\\Delta t+\\sigma W\\_{t\\_k})\n$$\n\n$W_{t_k}\\sim N(0,\\Delta t),\\Delta t=\\frac{T}{n},\\tau=\\{t_0=0<t_1<\\cdots<t_{N-1}<t_N=T\\}$\n\nthe value of the CPPI portfolio is \n\n$$\nV\\_{t\\_{k+1}}^\\tau=e^{r(t\\_{k+1}-min(\\nu,k+1)}((V\\_0-F\\_0)\\prod_{i=1}^{min(\\nu,k+1)}(m\\frac{S\\_{t\\_i}}{S\\_{t\\_{i-1}}}-(m-1)e^{r\\Delta t})+F\\_{t\\_{min(\\nu,k+1)}})\n$$\n\nin this framework, we consider the interest rate between the adjustments\n\nself-financed, so the expected the portfolio terminal value under the risk neutral probability measure is $e^{rT}V_0$. the CPPI is sold as a product with a capital guarantee, so for the investors the value of the CPPI is not equal to $V_0$\n\nthe payoff at maturity of the discrete CPPI is $CPPI_T=max\\{V_T,F_T\\}$\n\nthe expected value of the portfolio at maturity is composed of two parts:\n\n$$\n\\mathbb{E}^Q[CPPI]=\\mathbb{E}^Q[CPPI_T\\vert C_1]+\\mathbb{E}^Q[CPPI_T\\vert C_2]\n$$\n\n$C_1$ means the portfolio at maturity does not fall below the floor over $[0,T]$\n\n1. when the strike price $K$ is equal to the value of the guarantee at maturity $F_T$, the option ends up in the money if $C_{t_{k+1}}^\\tau>0$, then a portfolio composed by the option on a CPPI with $K=F_T$ and a zero coupon bond with nominal value $K$ is **exactly equal** to a CPPI with floor $F$\n2. when the strike price is higher than the guarantee amount at maturity $K\\ge F_T$, the option ends up in the money if the CPPI has not fallen below the floor, and if the value is greater than the strike price $K$.\n\n## Structured product written on GMEE-CPPI\n\nthe options linked to portfolio insurance strategies can be a suitable way to obtain a downside protection, by it is unable to offer an equity market participation in the event that after draw down, the risky asset recover nicely.\n\ndefine a minimum threshold which is always invested in the risky asset — *guaranteed minimum equity exposure* (GMEE-CPPI)\n\nGMEE $\\alpha_{min}$ \n\n$$\n\\alpha_t:=max\\{min\\{\\frac{m(V_t^{CPPI}-F_t)}{V_t^{CPPI}},L\\},\\alpha_{min}\\}\n$$\n\nthe equity participation will never go below $\\alpha_{min}$, but it means the CPPI allocation implemented in a real portfolio might not be able to protect the invested capital\n\ncombination of CPPI and OBPI:\n\n1. a proportion of the initial portfolio value invested in time-congruent zero-coupon bond following the OBPI\n2. the remaining part of the portfolio put into an exotic call option linked to a GMEE-CPPI where the CPPI has an equity index as risky asset\n","source":"_posts/Managing cash-in risk embedded in Portfolio Insurance strategies.md","raw":"---\nlayout: posts\ntitle: Managing cash-in risk embedded in Portfolio Insurance strategies\ndate: 2022-04-18\ncategories: 学习笔记\ntags: [金融,数学]\n\n---\n\n<head>\n <script src=\"https://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML\" type=\"text/javascript\"></script>\n <script type=\"text/x-mathjax-config\">\n MathJax.Hub.Config({\n tex2jax: {\n skipTags: ['script', 'noscript', 'style', 'textarea', 'pre'],\n inlineMath: [['$','$']]\n }\n });\n </script>\n</head>\n\n# Managing cash-in risk embedded in Portfolio\nInsurance strategies: a review\n\nthe presence of an insurance could have convinced the investors to not leave the market, and **take risk**\n\nPerold and Sharpe: 3 different insurance strategies: option-based \\ option-duplicating \\ derivative independent \n\noption-based: buy zero-coupon bond maturity equals investment time horizon + risky option\n\noption-duplicating: replicate option with a self-financing strategy (overcome the lack of liquidity)\n\nlow interest rate level reduce the available risk budgets. both a sustainable equity & capital protection? **dynamically allocating both in risky and riskless assets** mostly used—CPPI\n\n**the problem of CPPI:**\n\nafter a severe market draw-down, the risk budget **erases** — cash-in risk\n\n1. the remaining portfolio value shifted into the riskless asset, might not guarantee\n2. subsequent rises of the risky asset\n\n# OBPI\n\nkey: ensuring a minimal terminal portfolio value\n\n$V_t^{OBPI}=qB_t+pC(t,S_t,K)$\n\nthe strategy is static, no trading occurs in $(0,T)$\n\nif the option whose strike price equal to the wealth to be immunized are not traded on the market, investors must replicate the option using hedge strategies. But the incompleteness...\n\n# CPPI\n\nthe value of the portfolio at maturity $V_T^{CPPI}$ is higher than a guaranteed amount $G$ a proportion (PL) of the initially invested amount $V_0^{CPPI}$\n\nfloor $F_t=F_T(1+r)^{-(T-t)},F_T=G$\n\n*cushion $C_t$*, the difference between $V_t$ and $F_t$. exposure to risky asset $E_t=m\\times C_t$, $m$ is the multiplier. the strategy is self-financed, so the rest of the portfolio $V_t-E_t$ is invested into risk-free asset.\n\nto avoid excessive equity exposure, $E_t$ is bounded to be at most $LEV\\cdot V_t^{CPPI}$\n\nthe proportion of wealth invested to the risky asset:\n\n$$\n\\alpha_t^{CPPI}=\\min\\{\\frac{m(V_t^{CPPI}-F_t)}{V_t^{CPPI}},LEV\\}\\\\\\\\\\beta_t=1-\\alpha_t\n$$\n\n## CPPI with continuous rebalancing\n\nfloor process $F=\\{F_t\\}_{t\\in[0,T]}$, the dynamic is $dF_t=rF_tdt,F_0=G\\cdot e^{-rT}$, $W_t$ is a standard Brownian motion in real world measure $\\mathbb{P}$\n\n$$\ndV_t=mC_t\\frac{dS_t}{S_t}+(V_t-mC_t)rdt\\\\\\dS_t=r S_tdt+\\sigma S_tdW_t^\\mathbb{P}\\\\\\\\\\frac{dC_t}{C_t}=((1-m)r+\\mu m)dt+m\\sigma dW_t^\\mathbb{P}\\\\\\C_t=C_0\\exp(rt+m(\\mu-r)t+m\\sigma W_t^\\mathbb{P}-\\frac{m^2\\sigma^2t}{2})\\\\\\\\=C_0\\exp(r(1-m)t+\\frac{m(1-m)\\sigma^2t}{2})(\\frac{S_t}{S_0})^m\\\\\\V_0=C_0+F_0\\to C_0=G/PL-Ge^{-rT}\\\\\\V_T=C_T+G=G+\\frac{G}{PL}(1-PLe^{-rT})\\exp((rT+\\frac{m\\sigma^2T}{2})(1-m))(\\frac{S_T}{S_0})^m\n$$\n\nthe CPPI strategy is equivalent to taking a long position in a zero-coupon bond with nominal $G$ to guarantee the capital at maturity and investing the remaining sum into a risky asset which has $m$ times the excess return and $m$ times the volatility of $S$ and is perfectly correlated with $S$.\n\nthere is non zero probability that during a sudden downside movement of the underlying asset, the fund manager will have no time to readjust the portfolio. then it goes crashing through the floor.\n\n## CPPI with discrete time rebalancing\n\ndiscrete time CPPI:\n\n$$\n\\tau=\\{t_0=0<t_1<\\cdots<t_{n-1}=T\\}\\\\\\C_{t_{k+1}}^\\tau=C_{t_0}^\\tau\\prod_{i=1}^{min(\\nu,k+1)}(m\\frac{S_{t_i}}{S_{t_{i-1}}}-(m-1))\\\\\\nu:=min(t_k\\in\\tau\\vert V_{t_K}^\\tau-G),\\infty \\text{if not attained}\\\\\\phi_t^{(S),\\tau}:=max(\\frac{mC_{t_k}^\\tau}{S_{t_k}},0)\n$$\n\nlocal shortfall probability\n\nshortfall probability\n\nexpected shortfall\n\nhow to ensure the effectiveness of CPPI strategy?\n\n1. given an estimate for $\\mu$ and $\\sigma$, determine the value of multiplier and the number of rebalances $n$ to let the probability of falling below the guarantee above a confidence level\n2. base on large deviations methods, estimate the possible losses between two consecutive trading dates\n\n## CPPI in presence of jump in asset price\n\nno relax on continuous trading assumptions, we introduce jumps in the risky asset\n\nthe cash-in risk cannot be attributed exclusively to trading restriction\n\n$$\ndB_t=rB_tdt,B_0=b\\\\\\\\dS_t=S_{t-}dZ_t\n$$\n\n$Z$ is a possible discontinuous driving process, modeled as semi-martingale, to ensure the positivity of the price, we assume that $\\Delta Z_t>-1$, and $\\nu=\\inf(t\\ge 0,V_t\\le F_t)$, when $t<\\nu$:\n\n$$\ndV_t=m(V_{t-}-F_t)\\frac{dS_t-}{S_{t-}}+(V_{t-}-m(V_{t-}-F_t))\\frac{dB_t}{B_t}\\\\\\frac{dC_t}{C_t-}=mdZ_t+(1-m)rdt\n$$\n\nintroduce the discounted cushion $C_t^*=C_t/B_t$\n\n$$\n\\frac{dC_t^*}{C_{t-}^*}=m(dZ_t-rdt)=mdL_t,L_t=L_0+\\int_0^tdZ_s-rds\\\\\\\\C_t^*=C_0\\mathcal{E}(mL)_t\n$$\n\nat time $\\nu$, all the portfolio is invested into risk-free asset and when $t\\ge \\nu$, the value of $C_t^*$ remains constant. Define $\\tilde{C}\\_t=C_{t\\wedge\\nu}^*=C\\_0^*\\mathcal{E}(mL)\\_{t\\wedge \\nu}$\n\nit can become negative in presence of negative jumps of sufficient size of stock price.\n\n# Some extensions of CPPI allocation strategy\n\n## Time-Invariant Portfolio Protection (TIPP)\n\nmodifies the floor:\n\n$$\n\\tilde{F}\\_t=max(F\\_t,PL\\cdot \\sup_{s\\le t} V\\_s)\n$$\n\n$PL$ is the protection level. the floor will jump up with the portfolio value in order to reduce the risky asset allocation when the market peaks\n\nthe growth rate of the TIPP floor can be considered comparable to the portfolio in each instant of time\n\nless exposure to the risky asset, change more smoothly over time, the overall return will be generally lower\n\n## Variable Proportion Portfolio Insurance (VPPI)\n\nmake the multiplier dynamic\n\nEPPI: the multiplier changes like this:\n\nat $t=0$ the investor fix a reference price for the risky asset rebalancing $S^{(0)}$,\n\n$$\nm_t=\\eta+\\exp(aln(\\frac{S^{(1)}}{S^{(0)}}))\n$$\n\n$\\eta>1$ is an arbitrary constant, and the rest is the dynamic multiple adjustment factor (DMAF)\n\nwhen the stock price goes up, the mechanism of the EPPI strategy creates more number of holding shares to perform an upside capture\n\nfix the multiplier at each rebalancing date by considering a local quantile guarantee condition posed by $\\mathbb{P}\\_{t\\_k}(C\\_{t\\_{K+1}}>0\\vert C\\_{t\\_k}>0)=\\\\\\\\\\mathbb{P}\\_{t\\_k}(m\\_{t\\_k}\\frac{S\\_{t\\_{k+1}}}{S\\_{t\\_k}}-(m\\_{t\\_k}-1)>0)\\ge 1-\\epsilon$\n\nit implies an upper bound $\\bar{m}_{t_k}$, the precise number is determined by the distribution\n\n# Hedging gap risk embedded through options\n\nanother way to hedge gap risk embedded in portfolio insurance strategies is to use **options**\n\ntake a long position on an at-the-money put option on the CPPI portfolio with a strike price at least equal to the minimum value that the investor requires at maturity\n\nor take a long position on an at-the-money call option on the CPPI portfolio\n\nkey: model option on CPPI\n\n## Modeling option on CPPI\n\nthe discrete time process describing the evolution of the risky asset under the risk neutral probability measure $\\mathbb{Q}$ is:\n\n$$\n\\frac{S\n\\_{t\\_k}}{S\\_{t\\_{k+1}}}=\\exp((r-\\frac{\\sigma}{2})\\Delta t+\\sigma W\\_{t\\_k})\n$$\n\n$W_{t_k}\\sim N(0,\\Delta t),\\Delta t=\\frac{T}{n},\\tau=\\{t_0=0<t_1<\\cdots<t_{N-1}<t_N=T\\}$\n\nthe value of the CPPI portfolio is \n\n$$\nV\\_{t\\_{k+1}}^\\tau=e^{r(t\\_{k+1}-min(\\nu,k+1)}((V\\_0-F\\_0)\\prod_{i=1}^{min(\\nu,k+1)}(m\\frac{S\\_{t\\_i}}{S\\_{t\\_{i-1}}}-(m-1)e^{r\\Delta t})+F\\_{t\\_{min(\\nu,k+1)}})\n$$\n\nin this framework, we consider the interest rate between the adjustments\n\nself-financed, so the expected the portfolio terminal value under the risk neutral probability measure is $e^{rT}V_0$. the CPPI is sold as a product with a capital guarantee, so for the investors the value of the CPPI is not equal to $V_0$\n\nthe payoff at maturity of the discrete CPPI is $CPPI_T=max\\{V_T,F_T\\}$\n\nthe expected value of the portfolio at maturity is composed of two parts:\n\n$$\n\\mathbb{E}^Q[CPPI]=\\mathbb{E}^Q[CPPI_T\\vert C_1]+\\mathbb{E}^Q[CPPI_T\\vert C_2]\n$$\n\n$C_1$ means the portfolio at maturity does not fall below the floor over $[0,T]$\n\n1. when the strike price $K$ is equal to the value of the guarantee at maturity $F_T$, the option ends up in the money if $C_{t_{k+1}}^\\tau>0$, then a portfolio composed by the option on a CPPI with $K=F_T$ and a zero coupon bond with nominal value $K$ is **exactly equal** to a CPPI with floor $F$\n2. when the strike price is higher than the guarantee amount at maturity $K\\ge F_T$, the option ends up in the money if the CPPI has not fallen below the floor, and if the value is greater than the strike price $K$.\n\n## Structured product written on GMEE-CPPI\n\nthe options linked to portfolio insurance strategies can be a suitable way to obtain a downside protection, by it is unable to offer an equity market participation in the event that after draw down, the risky asset recover nicely.\n\ndefine a minimum threshold which is always invested in the risky asset — *guaranteed minimum equity exposure* (GMEE-CPPI)\n\nGMEE $\\alpha_{min}$ \n\n$$\n\\alpha_t:=max\\{min\\{\\frac{m(V_t^{CPPI}-F_t)}{V_t^{CPPI}},L\\},\\alpha_{min}\\}\n$$\n\nthe equity participation will never go below $\\alpha_{min}$, but it means the CPPI allocation implemented in a real portfolio might not be able to protect the invested capital\n\ncombination of CPPI and OBPI:\n\n1. a proportion of the initial portfolio value invested in time-congruent zero-coupon bond following the OBPI\n2. the remaining part of the portfolio put into an exotic call option linked to a GMEE-CPPI where the CPPI has an equity index as risky asset\n","slug":"Managing cash-in risk embedded in Portfolio Insurance strategies","published":1,"updated":"2022-04-18T08:50:49.177Z","_id":"cl24gxm420001x6pk4jbv8blv","comments":1,"photos":[],"link":"","content":"<head>\n <script src=\"https://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML\" type=\"text/javascript\"></script>\n <script type=\"text/x-mathjax-config\">\n MathJax.Hub.Config({\n tex2jax: {\n skipTags: ['script', 'noscript', 'style', 'textarea', 'pre'],\n inlineMath: [['$','$']]\n }\n });\n </script>\n</head>\n\n<h1 id=\"Managing-cash-in-risk-embedded-in-Portfolio\"><a href=\"#Managing-cash-in-risk-embedded-in-Portfolio\" class=\"headerlink\" title=\"Managing cash-in risk embedded in Portfolio\"></a>Managing cash-in risk embedded in Portfolio</h1><p>Insurance strategies: a review</p>\n<p>the presence of an insurance could have convinced the investors to not leave the market, and <strong>take risk</strong></p>\n<p>Perold and Sharpe: 3 different insurance strategies: option-based \\ option-duplicating \\ derivative independent </p>\n<p>option-based: buy zero-coupon bond maturity equals investment time horizon + risky option</p>\n<p>option-duplicating: replicate option with a self-financing strategy (overcome the lack of liquidity)</p>\n<p>low interest rate level reduce the available risk budgets. both a sustainable equity & capital protection? <strong>dynamically allocating both in risky and riskless assets</strong> mostly used—CPPI</p>\n<p><strong>the problem of CPPI:</strong></p>\n<p>after a severe market draw-down, the risk budget <strong>erases</strong> — cash-in risk</p>\n<ol>\n<li>the remaining portfolio value shifted into the riskless asset, might not guarantee</li>\n<li>subsequent rises of the risky asset</li>\n</ol>\n<h1 id=\"OBPI\"><a href=\"#OBPI\" class=\"headerlink\" title=\"OBPI\"></a>OBPI</h1><p>key: ensuring a minimal terminal portfolio value</p>\n<p>$V_t^{OBPI}=qB_t+pC(t,S_t,K)$</p>\n<p>the strategy is static, no trading occurs in $(0,T)$</p>\n<p>if the option whose strike price equal to the wealth to be immunized are not traded on the market, investors must replicate the option using hedge strategies. But the incompleteness…</p>\n<h1 id=\"CPPI\"><a href=\"#CPPI\" class=\"headerlink\" title=\"CPPI\"></a>CPPI</h1><p>the value of the portfolio at maturity $V_T^{CPPI}$ is higher than a guaranteed amount $G$ a proportion (PL) of the initially invested amount $V_0^{CPPI}$</p>\n<p>floor $F_t=F_T(1+r)^{-(T-t)},F_T=G$</p>\n<p><em>cushion $C_t$</em>, the difference between $V_t$ and $F_t$. exposure to risky asset $E_t=m\\times C_t$, $m$ is the multiplier. the strategy is self-financed, so the rest of the portfolio $V_t-E_t$ is invested into risk-free asset.</p>\n<p>to avoid excessive equity exposure, $E_t$ is bounded to be at most $LEV\\cdot V_t^{CPPI}$</p>\n<p>the proportion of wealth invested to the risky asset:</p>\n<p>$$<br>\\alpha_t^{CPPI}=\\min{\\frac{m(V_t^{CPPI}-F_t)}{V_t^{CPPI}},LEV}\\\\\\beta_t=1-\\alpha_t<br>$$</p>\n<h2 id=\"CPPI-with-continuous-rebalancing\"><a href=\"#CPPI-with-continuous-rebalancing\" class=\"headerlink\" title=\"CPPI with continuous rebalancing\"></a>CPPI with continuous rebalancing</h2><p>floor process $F={F_t}_{t\\in[0,T]}$, the dynamic is $dF_t=rF_tdt,F_0=G\\cdot e^{-rT}$, $W_t$ is a standard Brownian motion in real world measure $\\mathbb{P}$</p>\n<p>$$<br>dV_t=mC_t\\frac{dS_t}{S_t}+(V_t-mC_t)rdt\\\\dS_t=r S_tdt+\\sigma S_tdW_t^\\mathbb{P}\\\\\\frac{dC_t}{C_t}=((1-m)r+\\mu m)dt+m\\sigma dW_t^\\mathbb{P}\\\\C_t=C_0\\exp(rt+m(\\mu-r)t+m\\sigma W_t^\\mathbb{P}-\\frac{m^2\\sigma^2t}{2})\\\\=C_0\\exp(r(1-m)t+\\frac{m(1-m)\\sigma^2t}{2})(\\frac{S_t}{S_0})^m\\\\V_0=C_0+F_0\\to C_0=G/PL-Ge^{-rT}\\\\V_T=C_T+G=G+\\frac{G}{PL}(1-PLe^{-rT})\\exp((rT+\\frac{m\\sigma^2T}{2})(1-m))(\\frac{S_T}{S_0})^m<br>$$</p>\n<p>the CPPI strategy is equivalent to taking a long position in a zero-coupon bond with nominal $G$ to guarantee the capital at maturity and investing the remaining sum into a risky asset which has $m$ times the excess return and $m$ times the volatility of $S$ and is perfectly correlated with $S$.</p>\n<p>there is non zero probability that during a sudden downside movement of the underlying asset, the fund manager will have no time to readjust the portfolio. then it goes crashing through the floor.</p>\n<h2 id=\"CPPI-with-discrete-time-rebalancing\"><a href=\"#CPPI-with-discrete-time-rebalancing\" class=\"headerlink\" title=\"CPPI with discrete time rebalancing\"></a>CPPI with discrete time rebalancing</h2><p>discrete time CPPI:</p>\n<p>$$<br>\\tau={t_0=0<t_1<\\cdots<t_{n-1}=T}\\\\C_{t_{k+1}}^\\tau=C_{t_0}^\\tau\\prod_{i=1}^{min(\\nu,k+1)}(m\\frac{S_{t_i}}{S_{t_{i-1}}}-(m-1))\\\\nu:=min(t_k\\in\\tau\\vert V_{t_K}^\\tau-G),\\infty \\text{if not attained}\\\\phi_t^{(S),\\tau}:=max(\\frac{mC_{t_k}^\\tau}{S_{t_k}},0)<br>$$</p>\n<p>local shortfall probability</p>\n<p>shortfall probability</p>\n<p>expected shortfall</p>\n<p>how to ensure the effectiveness of CPPI strategy?</p>\n<ol>\n<li>given an estimate for $\\mu$ and $\\sigma$, determine the value of multiplier and the number of rebalances $n$ to let the probability of falling below the guarantee above a confidence level</li>\n<li>base on large deviations methods, estimate the possible losses between two consecutive trading dates</li>\n</ol>\n<h2 id=\"CPPI-in-presence-of-jump-in-asset-price\"><a href=\"#CPPI-in-presence-of-jump-in-asset-price\" class=\"headerlink\" title=\"CPPI in presence of jump in asset price\"></a>CPPI in presence of jump in asset price</h2><p>no relax on continuous trading assumptions, we introduce jumps in the risky asset</p>\n<p>the cash-in risk cannot be attributed exclusively to trading restriction</p>\n<p>$$<br>dB_t=rB_tdt,B_0=b\\\\dS_t=S_{t-}dZ_t<br>$$</p>\n<p>$Z$ is a possible discontinuous driving process, modeled as semi-martingale, to ensure the positivity of the price, we assume that $\\Delta Z_t>-1$, and $\\nu=\\inf(t\\ge 0,V_t\\le F_t)$, when $t<\\nu$:</p>\n<p>$$<br>dV_t=m(V_{t-}-F_t)\\frac{dS_t-}{S_{t-}}+(V_{t-}-m(V_{t-}-F_t))\\frac{dB_t}{B_t}\\\\frac{dC_t}{C_t-}=mdZ_t+(1-m)rdt<br>$$</p>\n<p>introduce the discounted cushion $C_t^*=C_t/B_t$</p>\n<p>$$<br>\\frac{dC_t^*}{C_{t-}^*}=m(dZ_t-rdt)=mdL_t,L_t=L_0+\\int_0^tdZ_s-rds\\\\C_t^*=C_0\\mathcal{E}(mL)_t<br>$$</p>\n<p>at time $\\nu$, all the portfolio is invested into risk-free asset and when $t\\ge \\nu$, the value of $C_t^*$ remains constant. Define $\\tilde{C}_t=C_{t\\wedge\\nu}^*=C_0^*\\mathcal{E}(mL)_{t\\wedge \\nu}$</p>\n<p>it can become negative in presence of negative jumps of sufficient size of stock price.</p>\n<h1 id=\"Some-extensions-of-CPPI-allocation-strategy\"><a href=\"#Some-extensions-of-CPPI-allocation-strategy\" class=\"headerlink\" title=\"Some extensions of CPPI allocation strategy\"></a>Some extensions of CPPI allocation strategy</h1><h2 id=\"Time-Invariant-Portfolio-Protection-TIPP\"><a href=\"#Time-Invariant-Portfolio-Protection-TIPP\" class=\"headerlink\" title=\"Time-Invariant Portfolio Protection (TIPP)\"></a>Time-Invariant Portfolio Protection (TIPP)</h2><p>modifies the floor:</p>\n<p>$$<br>\\tilde{F}_t=max(F_t,PL\\cdot \\sup_{s\\le t} V_s)<br>$$</p>\n<p>$PL$ is the protection level. the floor will jump up with the portfolio value in order to reduce the risky asset allocation when the market peaks</p>\n<p>the growth rate of the TIPP floor can be considered comparable to the portfolio in each instant of time</p>\n<p>less exposure to the risky asset, change more smoothly over time, the overall return will be generally lower</p>\n<h2 id=\"Variable-Proportion-Portfolio-Insurance-VPPI\"><a href=\"#Variable-Proportion-Portfolio-Insurance-VPPI\" class=\"headerlink\" title=\"Variable Proportion Portfolio Insurance (VPPI)\"></a>Variable Proportion Portfolio Insurance (VPPI)</h2><p>make the multiplier dynamic</p>\n<p>EPPI: the multiplier changes like this:</p>\n<p>at $t=0$ the investor fix a reference price for the risky asset rebalancing $S^{(0)}$,</p>\n<p>$$<br>m_t=\\eta+\\exp(aln(\\frac{S^{(1)}}{S^{(0)}}))<br>$$</p>\n<p>$\\eta>1$ is an arbitrary constant, and the rest is the dynamic multiple adjustment factor (DMAF)</p>\n<p>when the stock price goes up, the mechanism of the EPPI strategy creates more number of holding shares to perform an upside capture</p>\n<p>fix the multiplier at each rebalancing date by considering a local quantile guarantee condition posed by $\\mathbb{P}_{t_k}(C_{t_{K+1}}>0\\vert C_{t_k}>0)=\\\\\\mathbb{P}_{t_k}(m_{t_k}\\frac{S_{t_{k+1}}}{S_{t_k}}-(m_{t_k}-1)>0)\\ge 1-\\epsilon$</p>\n<p>it implies an upper bound $\\bar{m}_{t_k}$, the precise number is determined by the distribution</p>\n<h1 id=\"Hedging-gap-risk-embedded-through-options\"><a href=\"#Hedging-gap-risk-embedded-through-options\" class=\"headerlink\" title=\"Hedging gap risk embedded through options\"></a>Hedging gap risk embedded through options</h1><p>another way to hedge gap risk embedded in portfolio insurance strategies is to use <strong>options</strong></p>\n<p>take a long position on an at-the-money put option on the CPPI portfolio with a strike price at least equal to the minimum value that the investor requires at maturity</p>\n<p>or take a long position on an at-the-money call option on the CPPI portfolio</p>\n<p>key: model option on CPPI</p>\n<h2 id=\"Modeling-option-on-CPPI\"><a href=\"#Modeling-option-on-CPPI\" class=\"headerlink\" title=\"Modeling option on CPPI\"></a>Modeling option on CPPI</h2><p>the discrete time process describing the evolution of the risky asset under the risk neutral probability measure $\\mathbb{Q}$ is:</p>\n<p>$$<br>\\frac{S<br>_{t_k}}{S_{t_{k+1}}}=\\exp((r-\\frac{\\sigma}{2})\\Delta t+\\sigma W_{t_k})<br>$$</p>\n<p>$W_{t_k}\\sim N(0,\\Delta t),\\Delta t=\\frac{T}{n},\\tau={t_0=0<t_1<\\cdots<t_{N-1}<t_N=T}$</p>\n<p>the value of the CPPI portfolio is </p>\n<p>$$<br>V_{t_{k+1}}^\\tau=e^{r(t_{k+1}-min(\\nu,k+1)}((V_0-F_0)\\prod_{i=1}^{min(\\nu,k+1)}(m\\frac{S_{t_i}}{S_{t_{i-1}}}-(m-1)e^{r\\Delta t})+F_{t_{min(\\nu,k+1)}})<br>$$</p>\n<p>in this framework, we consider the interest rate between the adjustments</p>\n<p>self-financed, so the expected the portfolio terminal value under the risk neutral probability measure is $e^{rT}V_0$. the CPPI is sold as a product with a capital guarantee, so for the investors the value of the CPPI is not equal to $V_0$</p>\n<p>the payoff at maturity of the discrete CPPI is $CPPI_T=max{V_T,F_T}$</p>\n<p>the expected value of the portfolio at maturity is composed of two parts:</p>\n<p>$$<br>\\mathbb{E}^Q[CPPI]=\\mathbb{E}^Q[CPPI_T\\vert C_1]+\\mathbb{E}^Q[CPPI_T\\vert C_2]<br>$$</p>\n<p>$C_1$ means the portfolio at maturity does not fall below the floor over $[0,T]$</p>\n<ol>\n<li>when the strike price $K$ is equal to the value of the guarantee at maturity $F_T$, the option ends up in the money if $C_{t_{k+1}}^\\tau>0$, then a portfolio composed by the option on a CPPI with $K=F_T$ and a zero coupon bond with nominal value $K$ is <strong>exactly equal</strong> to a CPPI with floor $F$</li>\n<li>when the strike price is higher than the guarantee amount at maturity $K\\ge F_T$, the option ends up in the money if the CPPI has not fallen below the floor, and if the value is greater than the strike price $K$.</li>\n</ol>\n<h2 id=\"Structured-product-written-on-GMEE-CPPI\"><a href=\"#Structured-product-written-on-GMEE-CPPI\" class=\"headerlink\" title=\"Structured product written on GMEE-CPPI\"></a>Structured product written on GMEE-CPPI</h2><p>the options linked to portfolio insurance strategies can be a suitable way to obtain a downside protection, by it is unable to offer an equity market participation in the event that after draw down, the risky asset recover nicely.</p>\n<p>define a minimum threshold which is always invested in the risky asset — <em>guaranteed minimum equity exposure</em> (GMEE-CPPI)</p>\n<p>GMEE $\\alpha_{min}$ </p>\n<p>$$<br>\\alpha_t:=max{min{\\frac{m(V_t^{CPPI}-F_t)}{V_t^{CPPI}},L},\\alpha_{min}}<br>$$</p>\n<p>the equity participation will never go below $\\alpha_{min}$, but it means the CPPI allocation implemented in a real portfolio might not be able to protect the invested capital</p>\n<p>combination of CPPI and OBPI:</p>\n<ol>\n<li>a proportion of the initial portfolio value invested in time-congruent zero-coupon bond following the OBPI</li>\n<li>the remaining part of the portfolio put into an exotic call option linked to a GMEE-CPPI where the CPPI has an equity index as risky asset</li>\n</ol>\n","site":{"data":{}},"excerpt":"","more":"<head>\n <script src=\"https://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML\" type=\"text/javascript\"></script>\n <script type=\"text/x-mathjax-config\">\n MathJax.Hub.Config({\n tex2jax: {\n skipTags: ['script', 'noscript', 'style', 'textarea', 'pre'],\n inlineMath: [['$','$']]\n }\n });\n </script>\n</head>\n\n<h1 id=\"Managing-cash-in-risk-embedded-in-Portfolio\"><a href=\"#Managing-cash-in-risk-embedded-in-Portfolio\" class=\"headerlink\" title=\"Managing cash-in risk embedded in Portfolio\"></a>Managing cash-in risk embedded in Portfolio</h1><p>Insurance strategies: a review</p>\n<p>the presence of an insurance could have convinced the investors to not leave the market, and <strong>take risk</strong></p>\n<p>Perold and Sharpe: 3 different insurance strategies: option-based \\ option-duplicating \\ derivative independent </p>\n<p>option-based: buy zero-coupon bond maturity equals investment time horizon + risky option</p>\n<p>option-duplicating: replicate option with a self-financing strategy (overcome the lack of liquidity)</p>\n<p>low interest rate level reduce the available risk budgets. both a sustainable equity & capital protection? <strong>dynamically allocating both in risky and riskless assets</strong> mostly used—CPPI</p>\n<p><strong>the problem of CPPI:</strong></p>\n<p>after a severe market draw-down, the risk budget <strong>erases</strong> — cash-in risk</p>\n<ol>\n<li>the remaining portfolio value shifted into the riskless asset, might not guarantee</li>\n<li>subsequent rises of the risky asset</li>\n</ol>\n<h1 id=\"OBPI\"><a href=\"#OBPI\" class=\"headerlink\" title=\"OBPI\"></a>OBPI</h1><p>key: ensuring a minimal terminal portfolio value</p>\n<p>$V_t^{OBPI}=qB_t+pC(t,S_t,K)$</p>\n<p>the strategy is static, no trading occurs in $(0,T)$</p>\n<p>if the option whose strike price equal to the wealth to be immunized are not traded on the market, investors must replicate the option using hedge strategies. But the incompleteness…</p>\n<h1 id=\"CPPI\"><a href=\"#CPPI\" class=\"headerlink\" title=\"CPPI\"></a>CPPI</h1><p>the value of the portfolio at maturity $V_T^{CPPI}$ is higher than a guaranteed amount $G$ a proportion (PL) of the initially invested amount $V_0^{CPPI}$</p>\n<p>floor $F_t=F_T(1+r)^{-(T-t)},F_T=G$</p>\n<p><em>cushion $C_t$</em>, the difference between $V_t$ and $F_t$. exposure to risky asset $E_t=m\\times C_t$, $m$ is the multiplier. the strategy is self-financed, so the rest of the portfolio $V_t-E_t$ is invested into risk-free asset.</p>\n<p>to avoid excessive equity exposure, $E_t$ is bounded to be at most $LEV\\cdot V_t^{CPPI}$</p>\n<p>the proportion of wealth invested to the risky asset:</p>\n<p>$$<br>\\alpha_t^{CPPI}=\\min{\\frac{m(V_t^{CPPI}-F_t)}{V_t^{CPPI}},LEV}\\\\\\beta_t=1-\\alpha_t<br>$$</p>\n<h2 id=\"CPPI-with-continuous-rebalancing\"><a href=\"#CPPI-with-continuous-rebalancing\" class=\"headerlink\" title=\"CPPI with continuous rebalancing\"></a>CPPI with continuous rebalancing</h2><p>floor process $F={F_t}_{t\\in[0,T]}$, the dynamic is $dF_t=rF_tdt,F_0=G\\cdot e^{-rT}$, $W_t$ is a standard Brownian motion in real world measure $\\mathbb{P}$</p>\n<p>$$<br>dV_t=mC_t\\frac{dS_t}{S_t}+(V_t-mC_t)rdt\\\\dS_t=r S_tdt+\\sigma S_tdW_t^\\mathbb{P}\\\\\\frac{dC_t}{C_t}=((1-m)r+\\mu m)dt+m\\sigma dW_t^\\mathbb{P}\\\\C_t=C_0\\exp(rt+m(\\mu-r)t+m\\sigma W_t^\\mathbb{P}-\\frac{m^2\\sigma^2t}{2})\\\\=C_0\\exp(r(1-m)t+\\frac{m(1-m)\\sigma^2t}{2})(\\frac{S_t}{S_0})^m\\\\V_0=C_0+F_0\\to C_0=G/PL-Ge^{-rT}\\\\V_T=C_T+G=G+\\frac{G}{PL}(1-PLe^{-rT})\\exp((rT+\\frac{m\\sigma^2T}{2})(1-m))(\\frac{S_T}{S_0})^m<br>$$</p>\n<p>the CPPI strategy is equivalent to taking a long position in a zero-coupon bond with nominal $G$ to guarantee the capital at maturity and investing the remaining sum into a risky asset which has $m$ times the excess return and $m$ times the volatility of $S$ and is perfectly correlated with $S$.</p>\n<p>there is non zero probability that during a sudden downside movement of the underlying asset, the fund manager will have no time to readjust the portfolio. then it goes crashing through the floor.</p>\n<h2 id=\"CPPI-with-discrete-time-rebalancing\"><a href=\"#CPPI-with-discrete-time-rebalancing\" class=\"headerlink\" title=\"CPPI with discrete time rebalancing\"></a>CPPI with discrete time rebalancing</h2><p>discrete time CPPI:</p>\n<p>$$<br>\\tau={t_0=0<t_1<\\cdots<t_{n-1}=T}\\\\C_{t_{k+1}}^\\tau=C_{t_0}^\\tau\\prod_{i=1}^{min(\\nu,k+1)}(m\\frac{S_{t_i}}{S_{t_{i-1}}}-(m-1))\\\\nu:=min(t_k\\in\\tau\\vert V_{t_K}^\\tau-G),\\infty \\text{if not attained}\\\\phi_t^{(S),\\tau}:=max(\\frac{mC_{t_k}^\\tau}{S_{t_k}},0)<br>$$</p>\n<p>local shortfall probability</p>\n<p>shortfall probability</p>\n<p>expected shortfall</p>\n<p>how to ensure the effectiveness of CPPI strategy?</p>\n<ol>\n<li>given an estimate for $\\mu$ and $\\sigma$, determine the value of multiplier and the number of rebalances $n$ to let the probability of falling below the guarantee above a confidence level</li>\n<li>base on large deviations methods, estimate the possible losses between two consecutive trading dates</li>\n</ol>\n<h2 id=\"CPPI-in-presence-of-jump-in-asset-price\"><a href=\"#CPPI-in-presence-of-jump-in-asset-price\" class=\"headerlink\" title=\"CPPI in presence of jump in asset price\"></a>CPPI in presence of jump in asset price</h2><p>no relax on continuous trading assumptions, we introduce jumps in the risky asset</p>\n<p>the cash-in risk cannot be attributed exclusively to trading restriction</p>\n<p>$$<br>dB_t=rB_tdt,B_0=b\\\\dS_t=S_{t-}dZ_t<br>$$</p>\n<p>$Z$ is a possible discontinuous driving process, modeled as semi-martingale, to ensure the positivity of the price, we assume that $\\Delta Z_t>-1$, and $\\nu=\\inf(t\\ge 0,V_t\\le F_t)$, when $t<\\nu$:</p>\n<p>$$<br>dV_t=m(V_{t-}-F_t)\\frac{dS_t-}{S_{t-}}+(V_{t-}-m(V_{t-}-F_t))\\frac{dB_t}{B_t}\\\\frac{dC_t}{C_t-}=mdZ_t+(1-m)rdt<br>$$</p>\n<p>introduce the discounted cushion $C_t^*=C_t/B_t$</p>\n<p>$$<br>\\frac{dC_t^*}{C_{t-}^*}=m(dZ_t-rdt)=mdL_t,L_t=L_0+\\int_0^tdZ_s-rds\\\\C_t^*=C_0\\mathcal{E}(mL)_t<br>$$</p>\n<p>at time $\\nu$, all the portfolio is invested into risk-free asset and when $t\\ge \\nu$, the value of $C_t^*$ remains constant. Define $\\tilde{C}_t=C_{t\\wedge\\nu}^*=C_0^*\\mathcal{E}(mL)_{t\\wedge \\nu}$</p>\n<p>it can become negative in presence of negative jumps of sufficient size of stock price.</p>\n<h1 id=\"Some-extensions-of-CPPI-allocation-strategy\"><a href=\"#Some-extensions-of-CPPI-allocation-strategy\" class=\"headerlink\" title=\"Some extensions of CPPI allocation strategy\"></a>Some extensions of CPPI allocation strategy</h1><h2 id=\"Time-Invariant-Portfolio-Protection-TIPP\"><a href=\"#Time-Invariant-Portfolio-Protection-TIPP\" class=\"headerlink\" title=\"Time-Invariant Portfolio Protection (TIPP)\"></a>Time-Invariant Portfolio Protection (TIPP)</h2><p>modifies the floor:</p>\n<p>$$<br>\\tilde{F}_t=max(F_t,PL\\cdot \\sup_{s\\le t} V_s)<br>$$</p>\n<p>$PL$ is the protection level. the floor will jump up with the portfolio value in order to reduce the risky asset allocation when the market peaks</p>\n<p>the growth rate of the TIPP floor can be considered comparable to the portfolio in each instant of time</p>\n<p>less exposure to the risky asset, change more smoothly over time, the overall return will be generally lower</p>\n<h2 id=\"Variable-Proportion-Portfolio-Insurance-VPPI\"><a href=\"#Variable-Proportion-Portfolio-Insurance-VPPI\" class=\"headerlink\" title=\"Variable Proportion Portfolio Insurance (VPPI)\"></a>Variable Proportion Portfolio Insurance (VPPI)</h2><p>make the multiplier dynamic</p>\n<p>EPPI: the multiplier changes like this:</p>\n<p>at $t=0$ the investor fix a reference price for the risky asset rebalancing $S^{(0)}$,</p>\n<p>$$<br>m_t=\\eta+\\exp(aln(\\frac{S^{(1)}}{S^{(0)}}))<br>$$</p>\n<p>$\\eta>1$ is an arbitrary constant, and the rest is the dynamic multiple adjustment factor (DMAF)</p>\n<p>when the stock price goes up, the mechanism of the EPPI strategy creates more number of holding shares to perform an upside capture</p>\n<p>fix the multiplier at each rebalancing date by considering a local quantile guarantee condition posed by $\\mathbb{P}_{t_k}(C_{t_{K+1}}>0\\vert C_{t_k}>0)=\\\\\\mathbb{P}_{t_k}(m_{t_k}\\frac{S_{t_{k+1}}}{S_{t_k}}-(m_{t_k}-1)>0)\\ge 1-\\epsilon$</p>\n<p>it implies an upper bound $\\bar{m}_{t_k}$, the precise number is determined by the distribution</p>\n<h1 id=\"Hedging-gap-risk-embedded-through-options\"><a href=\"#Hedging-gap-risk-embedded-through-options\" class=\"headerlink\" title=\"Hedging gap risk embedded through options\"></a>Hedging gap risk embedded through options</h1><p>another way to hedge gap risk embedded in portfolio insurance strategies is to use <strong>options</strong></p>\n<p>take a long position on an at-the-money put option on the CPPI portfolio with a strike price at least equal to the minimum value that the investor requires at maturity</p>\n<p>or take a long position on an at-the-money call option on the CPPI portfolio</p>\n<p>key: model option on CPPI</p>\n<h2 id=\"Modeling-option-on-CPPI\"><a href=\"#Modeling-option-on-CPPI\" class=\"headerlink\" title=\"Modeling option on CPPI\"></a>Modeling option on CPPI</h2><p>the discrete time process describing the evolution of the risky asset under the risk neutral probability measure $\\mathbb{Q}$ is:</p>\n<p>$$<br>\\frac{S<br>_{t_k}}{S_{t_{k+1}}}=\\exp((r-\\frac{\\sigma}{2})\\Delta t+\\sigma W_{t_k})<br>$$</p>\n<p>$W_{t_k}\\sim N(0,\\Delta t),\\Delta t=\\frac{T}{n},\\tau={t_0=0<t_1<\\cdots<t_{N-1}<t_N=T}$</p>\n<p>the value of the CPPI portfolio is </p>\n<p>$$<br>V_{t_{k+1}}^\\tau=e^{r(t_{k+1}-min(\\nu,k+1)}((V_0-F_0)\\prod_{i=1}^{min(\\nu,k+1)}(m\\frac{S_{t_i}}{S_{t_{i-1}}}-(m-1)e^{r\\Delta t})+F_{t_{min(\\nu,k+1)}})<br>$$</p>\n<p>in this framework, we consider the interest rate between the adjustments</p>\n<p>self-financed, so the expected the portfolio terminal value under the risk neutral probability measure is $e^{rT}V_0$. the CPPI is sold as a product with a capital guarantee, so for the investors the value of the CPPI is not equal to $V_0$</p>\n<p>the payoff at maturity of the discrete CPPI is $CPPI_T=max{V_T,F_T}$</p>\n<p>the expected value of the portfolio at maturity is composed of two parts:</p>\n<p>$$<br>\\mathbb{E}^Q[CPPI]=\\mathbb{E}^Q[CPPI_T\\vert C_1]+\\mathbb{E}^Q[CPPI_T\\vert C_2]<br>$$</p>\n<p>$C_1$ means the portfolio at maturity does not fall below the floor over $[0,T]$</p>\n<ol>\n<li>when the strike price $K$ is equal to the value of the guarantee at maturity $F_T$, the option ends up in the money if $C_{t_{k+1}}^\\tau>0$, then a portfolio composed by the option on a CPPI with $K=F_T$ and a zero coupon bond with nominal value $K$ is <strong>exactly equal</strong> to a CPPI with floor $F$</li>\n<li>when the strike price is higher than the guarantee amount at maturity $K\\ge F_T$, the option ends up in the money if the CPPI has not fallen below the floor, and if the value is greater than the strike price $K$.</li>\n</ol>\n<h2 id=\"Structured-product-written-on-GMEE-CPPI\"><a href=\"#Structured-product-written-on-GMEE-CPPI\" class=\"headerlink\" title=\"Structured product written on GMEE-CPPI\"></a>Structured product written on GMEE-CPPI</h2><p>the options linked to portfolio insurance strategies can be a suitable way to obtain a downside protection, by it is unable to offer an equity market participation in the event that after draw down, the risky asset recover nicely.</p>\n<p>define a minimum threshold which is always invested in the risky asset — <em>guaranteed minimum equity exposure</em> (GMEE-CPPI)</p>\n<p>GMEE $\\alpha_{min}$ </p>\n<p>$$<br>\\alpha_t:=max{min{\\frac{m(V_t^{CPPI}-F_t)}{V_t^{CPPI}},L},\\alpha_{min}}<br>$$</p>\n<p>the equity participation will never go below $\\alpha_{min}$, but it means the CPPI allocation implemented in a real portfolio might not be able to protect the invested capital</p>\n<p>combination of CPPI and OBPI:</p>\n<ol>\n<li>a proportion of the initial portfolio value invested in time-congruent zero-coupon bond following the OBPI</li>\n<li>the remaining part of the portfolio put into an exotic call option linked to a GMEE-CPPI where the CPPI has an equity index as risky asset</li>\n</ol>\n"},{"layout":"posts","title":"WebChat聊天室","_content":"# WebChat聊天室\n\ngithub:https://github.com/Ryan-dev-design/WebChat\n## 依赖环境\n\n1. python 2.7.18(请确保使用正确的python版本,因为tornado-redis与高版本python可能出现兼容性问题)\n2. tornado\n3. redis-server\n4. sqlite3\n\n## 启动WebChat服务\n\n```\n$ redis-server (开启redis服务)\n$ python init_sqlite.py (第一次使用请运行,初始化数据库)\n$ python server.py (启动WebChat服务)\n在浏览器中访问 localhost:8200 即可开始使用WebChat\n```\n## 项目说明\n\n### 前端\n\n利用semantic-ui的ccs文件,进行页面美化(https://semantic-ui.com/)\n使用基于ajax的longpolling向后端传送数据\n\n### 后端\n\n采用redis的sub/pub机制获取信息\n利用sqlite3作为数据库\n\n## 项目功能\n\n1. 用户注册/登陆,有基本的密码验证机制\n2. 支持修改密码\n3. 支持通过搜索添加好友\n4. 支持通过在好友中搜索,并邀请好友进入聊天室\n\n## 场景展示\n注册账号\n.png)\n添加好友\n\n开始私聊\n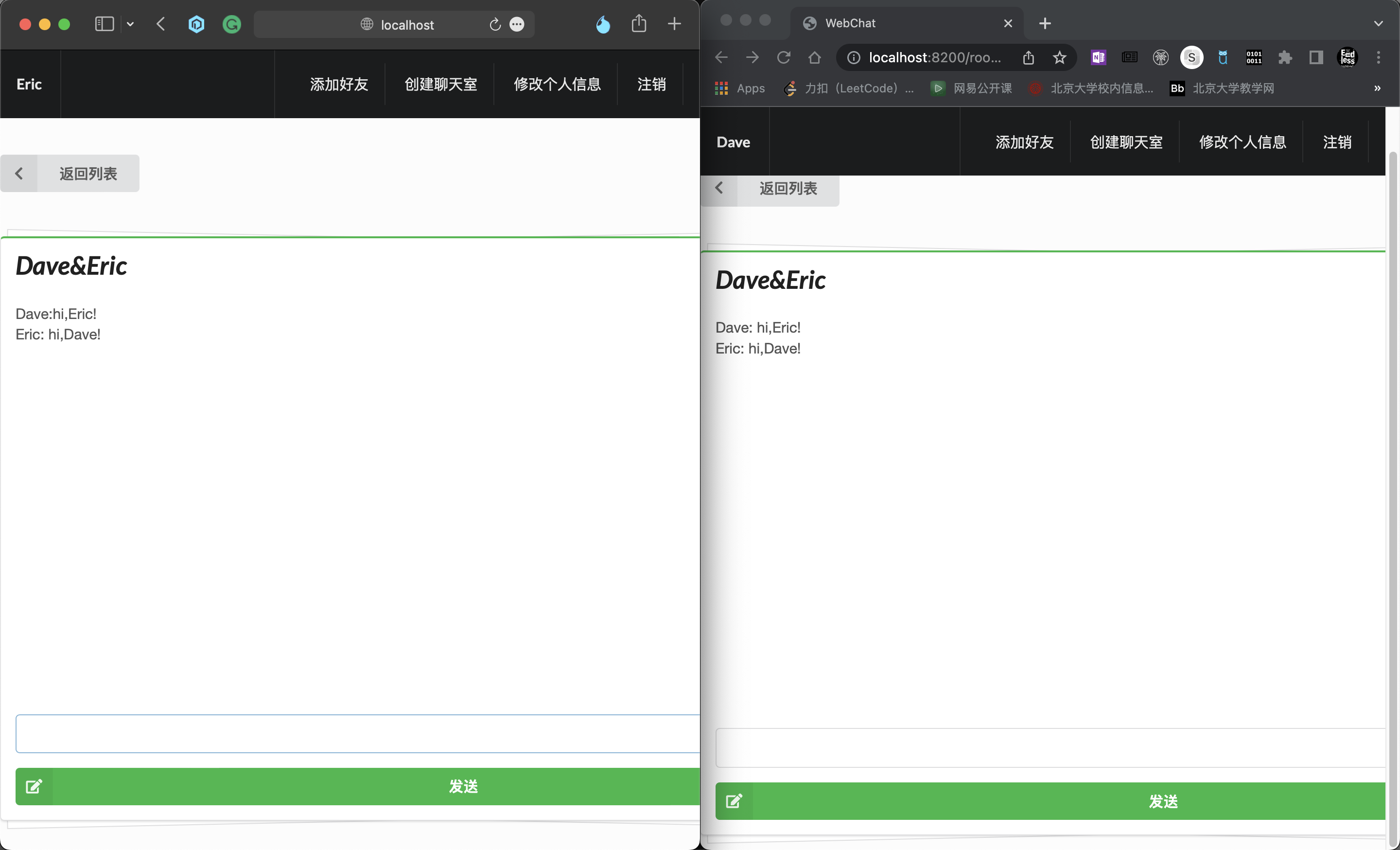\n创建讨论室\n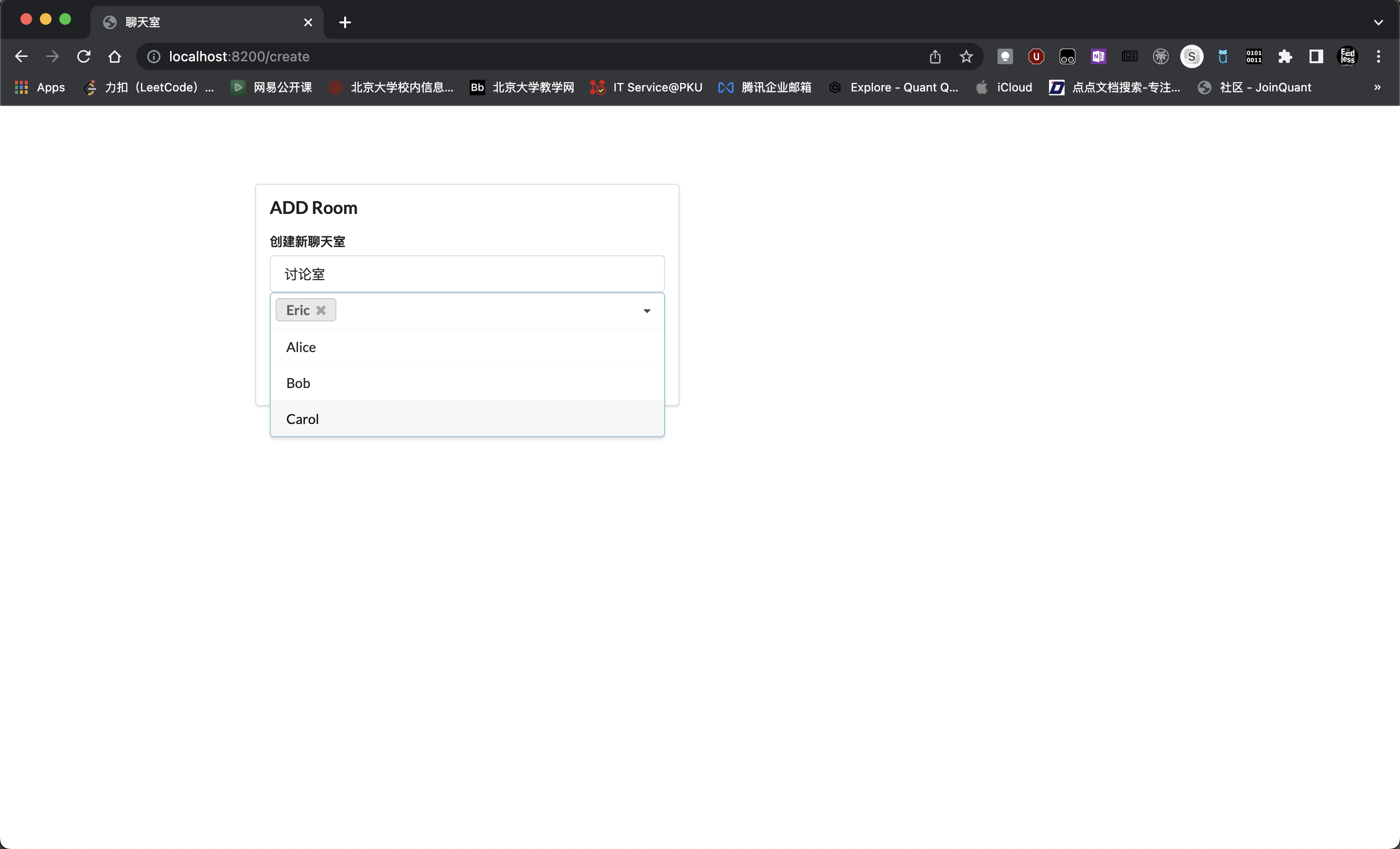\n修改密码\n","source":"_posts/WebChat.md","raw":"---\nlayout: posts\ntitle: WebChat聊天室\ncategories: 个人项目\ntags: [计算机]\n\n---\n# WebChat聊天室\n\ngithub:https://github.com/Ryan-dev-design/WebChat\n## 依赖环境\n\n1. python 2.7.18(请确保使用正确的python版本,因为tornado-redis与高版本python可能出现兼容性问题)\n2. tornado\n3. redis-server\n4. sqlite3\n\n## 启动WebChat服务\n\n```\n$ redis-server (开启redis服务)\n$ python init_sqlite.py (第一次使用请运行,初始化数据库)\n$ python server.py (启动WebChat服务)\n在浏览器中访问 localhost:8200 即可开始使用WebChat\n```\n## 项目说明\n\n### 前端\n\n利用semantic-ui的ccs文件,进行页面美化(https://semantic-ui.com/)\n使用基于ajax的longpolling向后端传送数据\n\n### 后端\n\n采用redis的sub/pub机制获取信息\n利用sqlite3作为数据库\n\n## 项目功能\n\n1. 用户注册/登陆,有基本的密码验证机制\n2. 支持修改密码\n3. 支持通过搜索添加好友\n4. 支持通过在好友中搜索,并邀请好友进入聊天室\n\n## 场景展示\n注册账号\n.png)\n添加好友\n\n开始私聊\n\n创建讨论室\n\n修改密码\n","slug":"WebChat","published":1,"date":"2022-05-10T19:44:50.645Z","updated":"2022-05-10T19:55:25.073Z","_id":"cl30kfnr10000vwpk00xy2okr","comments":1,"photos":[],"link":"","content":"<h1 id=\"WebChat聊天室\"><a href=\"#WebChat聊天室\" class=\"headerlink\" title=\"WebChat聊天室\"></a>WebChat聊天室</h1><p>github:<a href=\"https://github.com/Ryan-dev-design/WebChat\">https://github.com/Ryan-dev-design/WebChat</a></p>\n<h2 id=\"依赖环境\"><a href=\"#依赖环境\" class=\"headerlink\" title=\"依赖环境\"></a>依赖环境</h2><ol>\n<li>python 2.7.18(请确保使用正确的python版本,因为tornado-redis与高版本python可能出现兼容性问题)</li>\n<li>tornado</li>\n<li>redis-server</li>\n<li>sqlite3</li>\n</ol>\n<h2 id=\"启动WebChat服务\"><a href=\"#启动WebChat服务\" class=\"headerlink\" title=\"启动WebChat服务\"></a>启动WebChat服务</h2><figure class=\"highlight plaintext\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br></pre></td><td class=\"code\"><pre><span class=\"line\">$ redis-server (开启redis服务)</span><br><span class=\"line\">$ python init_sqlite.py (第一次使用请运行,初始化数据库)</span><br><span class=\"line\">$ python server.py (启动WebChat服务)</span><br><span class=\"line\">在浏览器中访问 localhost:8200 即可开始使用WebChat</span><br></pre></td></tr></table></figure>\n<h2 id=\"项目说明\"><a href=\"#项目说明\" class=\"headerlink\" title=\"项目说明\"></a>项目说明</h2><h3 id=\"前端\"><a href=\"#前端\" class=\"headerlink\" title=\"前端\"></a>前端</h3><p>利用semantic-ui的ccs文件,进行页面美化(<a href=\"https://semantic-ui.com/\">https://semantic-ui.com/</a>)<br>使用基于ajax的longpolling向后端传送数据</p>\n<h3 id=\"后端\"><a href=\"#后端\" class=\"headerlink\" title=\"后端\"></a>后端</h3><p>采用redis的sub/pub机制获取信息<br>利用sqlite3作为数据库</p>\n<h2 id=\"项目功能\"><a href=\"#项目功能\" class=\"headerlink\" title=\"项目功能\"></a>项目功能</h2><ol>\n<li>用户注册/登陆,有基本的密码验证机制</li>\n<li>支持修改密码</li>\n<li>支持通过搜索添加好友</li>\n<li>支持通过在好友中搜索,并邀请好友进入聊天室</li>\n</ol>\n<h2 id=\"场景展示\"><a href=\"#场景展示\" class=\"headerlink\" title=\"场景展示\"></a>场景展示</h2><p>注册账号<br><img src=\"https://raw.githubusercontent.com/Ryan-dev-design/WebChat/master/pic/Screen%20Shot%202022-05-11%20at%2003.01.25%20(2).png\" alt=\"alt 注册\"><br>添加好友<br><img src=\"https://raw.githubusercontent.com/Ryan-dev-design/WebChat/master/pic/Screen%20Shot%202022-05-11%20at%2003.05.50.png\" alt=\"alt 添加好友\"><br>开始私聊<br><img src=\"https://raw.githubusercontent.com/Ryan-dev-design/WebChat/master/pic/Screen%20Shot%202022-05-11%20at%2003.22.54.png\" alt=\"alt 私聊\"><br>创建讨论室<br><img src=\"https://raw.githubusercontent.com/Ryan-dev-design/WebChat/master/pic/Screen%20Shot%202022-05-11%20at%2003.23.33.png\" alt=\"alt 讨论室\"><br>修改密码<br><img src=\"https://raw.githubusercontent.com/Ryan-dev-design/WebChat/master/pic/Screen%20Shot%202022-05-11%20at%2003.24.31.png\" alt=\"alt 修改密码\"></p>\n","site":{"data":{}},"excerpt":"","more":"<h1 id=\"WebChat聊天室\"><a href=\"#WebChat聊天室\" class=\"headerlink\" title=\"WebChat聊天室\"></a>WebChat聊天室</h1><p>github:<a href=\"https://github.com/Ryan-dev-design/WebChat\">https://github.com/Ryan-dev-design/WebChat</a></p>\n<h2 id=\"依赖环境\"><a href=\"#依赖环境\" class=\"headerlink\" title=\"依赖环境\"></a>依赖环境</h2><ol>\n<li>python 2.7.18(请确保使用正确的python版本,因为tornado-redis与高版本python可能出现兼容性问题)</li>\n<li>tornado</li>\n<li>redis-server</li>\n<li>sqlite3</li>\n</ol>\n<h2 id=\"启动WebChat服务\"><a href=\"#启动WebChat服务\" class=\"headerlink\" title=\"启动WebChat服务\"></a>启动WebChat服务</h2><figure class=\"highlight plaintext\"><table><tr><td class=\"gutter\"><pre><span class=\"line\">1</span><br><span class=\"line\">2</span><br><span class=\"line\">3</span><br><span class=\"line\">4</span><br></pre></td><td class=\"code\"><pre><span class=\"line\">$ redis-server (开启redis服务)</span><br><span class=\"line\">$ python init_sqlite.py (第一次使用请运行,初始化数据库)</span><br><span class=\"line\">$ python server.py (启动WebChat服务)</span><br><span class=\"line\">在浏览器中访问 localhost:8200 即可开始使用WebChat</span><br></pre></td></tr></table></figure>\n<h2 id=\"项目说明\"><a href=\"#项目说明\" class=\"headerlink\" title=\"项目说明\"></a>项目说明</h2><h3 id=\"前端\"><a href=\"#前端\" class=\"headerlink\" title=\"前端\"></a>前端</h3><p>利用semantic-ui的ccs文件,进行页面美化(<a href=\"https://semantic-ui.com/\">https://semantic-ui.com/</a>)<br>使用基于ajax的longpolling向后端传送数据</p>\n<h3 id=\"后端\"><a href=\"#后端\" class=\"headerlink\" title=\"后端\"></a>后端</h3><p>采用redis的sub/pub机制获取信息<br>利用sqlite3作为数据库</p>\n<h2 id=\"项目功能\"><a href=\"#项目功能\" class=\"headerlink\" title=\"项目功能\"></a>项目功能</h2><ol>\n<li>用户注册/登陆,有基本的密码验证机制</li>\n<li>支持修改密码</li>\n<li>支持通过搜索添加好友</li>\n<li>支持通过在好友中搜索,并邀请好友进入聊天室</li>\n</ol>\n<h2 id=\"场景展示\"><a href=\"#场景展示\" class=\"headerlink\" title=\"场景展示\"></a>场景展示</h2><p>注册账号<br><img src=\"https://raw.githubusercontent.com/Ryan-dev-design/WebChat/master/pic/Screen%20Shot%202022-05-11%20at%2003.01.25%20(2).png\" alt=\"alt 注册\"><br>添加好友<br><img src=\"https://raw.githubusercontent.com/Ryan-dev-design/WebChat/master/pic/Screen%20Shot%202022-05-11%20at%2003.05.50.png\" alt=\"alt 添加好友\"><br>开始私聊<br><img src=\"https://raw.githubusercontent.com/Ryan-dev-design/WebChat/master/pic/Screen%20Shot%202022-05-11%20at%2003.22.54.png\" alt=\"alt 私聊\"><br>创建讨论室<br><img src=\"https://raw.githubusercontent.com/Ryan-dev-design/WebChat/master/pic/Screen%20Shot%202022-05-11%20at%2003.23.33.png\" alt=\"alt 讨论室\"><br>修改密码<br><img src=\"https://raw.githubusercontent.com/Ryan-dev-design/WebChat/master/pic/Screen%20Shot%202022-05-11%20at%2003.24.31.png\" alt=\"alt 修改密码\"></p>\n"},{"title":"Back","date":"2023-06-08T17:24:34.000Z","updated":"2023-06-08T17:24:34.000Z","_content":"# I'm Back\n","source":"_posts/Back.md","raw":"---\ntitle: Back\ndate: 2023-06-09 01:24:34\nupdated: 2023-06-09 01:24:34\ntags:\n---\n# I'm Back\n","slug":"Back","published":1,"comments":1,"layout":"post","photos":[],"link":"","_id":"clineson00000k9pkgcdpbzrh","content":"<h1 id=\"I’m-Back\"><a href=\"#I’m-Back\" class=\"headerlink\" title=\"I’m Back\"></a>I’m Back</h1>","site":{"data":{}},"excerpt":"","more":"<h1 id=\"I’m-Back\"><a href=\"#I’m-Back\" class=\"headerlink\" title=\"I’m Back\"></a>I’m Back</h1>"}],"PostAsset":[],"PostCategory":[{"post_id":"cl0110i7000019jpkhgg10eet","category_id":"cl0110i7600039jpk6cbucvk0","_id":"cl0110i7a00069jpkgrlqgpos"},{"post_id":"cl24gxm3z0000x6pkhpk029qg","category_id":"cl0110i7600039jpk6cbucvk0","_id":"cl24gxm460004x6pkakuta0x6"},{"post_id":"cl24gxm420001x6pk4jbv8blv","category_id":"cl0110i7600039jpk6cbucvk0","_id":"cl24gxm460006x6pkals79bey"},{"post_id":"cl30kfnr10000vwpk00xy2okr","category_id":"cl30kgq3500006fpk8jqgeljk","_id":"cl30kgq3800036fpk7jou3jiq"}],"PostTag":[{"post_id":"cl0110i7000019jpkhgg10eet","tag_id":"cl0110i7800049jpketw5gnyg","_id":"cl0110i7a00079jpkequpfs00"},{"post_id":"cl0110i7000019jpkhgg10eet","tag_id":"cl0110i7900059jpk19d59wo1","_id":"cl0110i7a00089jpk93wr26a7"},{"post_id":"cl24gxm420001x6pk4jbv8blv","tag_id":"cl0110i7800049jpketw5gnyg","_id":"cl24gxm460003x6pk57zl780a"},{"post_id":"cl24gxm420001x6pk4jbv8blv","tag_id":"cl0110i7900059jpk19d59wo1","_id":"cl24gxm460005x6pkfqo4f424"},{"post_id":"cl24gxm3z0000x6pkhpk029qg","tag_id":"cl24gxm440002x6pk85gmfg39","_id":"cl24gxm470007x6pkbpg0bsv2"},{"post_id":"cl30kfnr10000vwpk00xy2okr","tag_id":"cl30kgq3700016fpk6xrlhikf","_id":"cl30kgq3800026fpkg19rf0gq"}],"Tag":[{"name":"金融","_id":"cl0110i7800049jpketw5gnyg"},{"name":"数学","_id":"cl0110i7900059jpk19d59wo1"},{"name":"经济","_id":"cl24gxm440002x6pk85gmfg39"},{"name":"计算机","_id":"cl30kgq3700016fpk6xrlhikf"}]}}