Releases · PennyLaneAI/pennylane

14 Dec 07:47

antalszava

v0.20.0

8fdf587

Release 0.20.0

New features since last release

Shiny new circuit drawer!🎨🖌️

PennyLane now supports drawing a QNode with matplotlib! (#1803) (#1811) (#1931) (#1954)

dev = qml.device("default.qubit", wires=4)

@qml.qnode(dev)
def circuit(x, z):
    qml.QFT(wires=(0,1,2,3))
    qml.Toffoli(wires=(0,1,2))
    qml.CSWAP(wires=(0,2,3))
    qml.RX(x, wires=0)
    qml.CRZ(z, wires=(3,0))
    return qml.expval(qml.PauliZ(0))
fig, ax = qml.draw_mpl(circuit)(1.2345, 1.2345)
fig.show()

New and improved quantum-aware optimizers

Added qml.LieAlgebraOptimizer, a new quantum-aware Lie Algebra optimizer that allows one to perform gradient descent on the special unitary group. (#1911)

dev = qml.device("default.qubit", wires=2)
H = -1.0 * qml.PauliX(0) - qml.PauliZ(1) - qml.PauliY(0) @ qml.PauliX(1)

@qml.qnode(dev)
def circuit():
    qml.RX(0.1, wires=[0])
    qml.RY(0.5, wires=[1])
    qml.CNOT(wires=[0,1])
    qml.RY(0.6, wires=[0])
    return qml.expval(H)
opt = qml.LieAlgebraOptimizer(circuit=circuit, stepsize=0.1)

Note that, unlike other optimizers, the LieAlgebraOptimizer accepts a QNode with no parameters, and instead grows the circuit by pending operations during the optimization:

>>> circuit()
tensor(-1.3351865, requires_grad=True)
>>> circuit1, cost = opt.step_and_cost()
>>> circuit1()
tensor(-1.99378872, requires_grad=True)

For more details, see the LieAlgebraOptimizer documentation.

The qml.metric_tensor transform can now be used to compute the full tensor, beyond the block diagonal approximation. (#1725)

This is performed using Hadamard tests, and requires an additional wire on the device to execute the circuits produced by the transform, as compared to the number of wires required by the original circuit. The transform defaults to computing the full tensor, which can be controlled by the approx keyword argument.

As an example, consider the QNode
```
dev = qml.device("default.qubit", wires=3)

@qml.qnode(dev)
def circuit(weights):
    qml.RX(weights[0], wires=0)
    qml.RY(weights[1], wires=0)
    qml.CNOT(wires=[0, 1])
    qml.RZ(weights[2], wires=1)
    return qml.expval(qml.PauliZ(0) @ qml.PauliZ(1))

weights = np.array([0.2, 1.2, -0.9], requires_grad=True)
```
Then we can compute the (block) diagonal metric tensor as before, now using the approx="block-diag" keyword:
```
>>> qml.metric_tensor(circuit, approx="block-diag")(weights)
[[0.25       0.         0.        ]
 [0.         0.24013262 0.        ]
 [0.         0.         0.21846983]]
```
Instead, we now can also compute the full metric tensor, using Hadamard tests on the additional wire of the device:
```
>>> qml.metric_tensor(circuit)(weights)
[[ 0.25        0.         -0.23300977]
 [ 0.          0.24013262  0.01763859]
 [-0.23300977  0.01763859  0.21846983]]
```
See the metric tensor documentation for more information and usage details.

Faster performance with optimized quantum workflows

The QNode has been re-written to support batch execution across the board, custom gradients, better decomposition strategies, and higher-order derivatives. (#1807) (#1969)
- Internally, if multiple circuits are generated for simultaneous execution, they will be packaged into a single job for execution on the device. This can lead to significant performance improvement when executing the QNode on remote quantum hardware or simulator devices with parallelization capabilities.
- Custom gradient transforms can be specified as the differentiation method:
```
@qml.gradients.gradient_transform
def my_gradient_transform(tape):
    ...
    return tapes, processing_fn

@qml.qnode(dev, diff_method=my_gradient_transform)
def circuit():
```
For breaking changes related to the use of the new QNode, refer to the Breaking Changes section.

Note that the old QNode remains accessible at @qml.qnode_old.qnode, however this will be removed in the next release.

Custom decompositions can now be applied to operations at the device level. (#1900)

For example, suppose we would like to implement the following QNode:

def circuit(weights):
    qml.BasicEntanglerLayers(weights, wires=[0, 1, 2])
    return qml.expval(qml.PauliZ(0))

original_dev = qml.device("default.qubit", wires=3)
original_qnode = qml.QNode(circuit, original_dev)

>>> weights = np.array([[0.4, 0.5, 0.6]])
>>> print(qml.draw(original_qnode, expansion_strategy="device")(weights))
 0: ──RX(0.4)──╭C──────╭X──┤ ⟨Z⟩
 1: ──RX(0.5)──╰X──╭C──│───┤
 2: ──RX(0.6)──────╰X──╰C──┤

Now, let's swap out the decomposition of the CNOT gate into CZ and Hadamard, and furthermore the decomposition of Hadamard into RZ and RY rather than the decomposition already available in PennyLane. We define the two decompositions like so, and pass them to a device:

def custom_cnot(wires):
    return [
        qml.Hadamard(wires=wires[1]),
        qml.CZ(wires=[wires[0], wires[1]]),
        qml.Hadamard(wires=wires[1])
    ]

def custom_hadamard(wires):
    return [
        qml.RZ(np.pi, wires=wires),
        qml.RY(np.pi / 2, wires=wires)
    ]

# Can pass the operation itself, or a string
custom_decomps = {qml.CNOT : custom_cnot, "Hadamard" : custom_hadamard}

decomp_dev = qml.device("default.qubit", wires=3, custom_decomps=custom_decomps)
decomp_qnode = qml.QNode(circuit, decomp_dev)

Now when we draw or run a QNode on this device, the gates will be expanded according to our specifications:

>>> print(qml.draw(decomp_qnode, expansion_strategy="device")(weights))
 0: ──RX(0.4)──────────────────────╭C──RZ(3.14)──RY(1.57)──────────────────────────╭Z──RZ(3.14)──RY(1.57)──┤ ⟨Z⟩
 1: ──RX(0.5)──RZ(3.14)──RY(1.57)──╰Z──RZ(3.14)──RY(1.57)──╭C──────────────────────│───────────────────────┤
 2: ──RX(0.6)──RZ(3.14)──RY(1.57)──────────────────────────╰Z──RZ(3.14)──RY(1.57)──╰C──────────────────────┤

A separate context manager, set_decomposition, has also been implemented to enable application of custom decompositions on devices that have already been created.

>>> with qml.transforms.set_decomposition(custom_decomps, original_dev):
...     print(qml.draw(original_qnode, expansion_strategy="device")(weights))
 0: ──RX(0.4)──────────────────────╭C──RZ(3.14)──RY(1.57)──────────────────────────╭Z──RZ(3.14)──RY(1.57)──┤ ⟨Z⟩
 1: ──RX(0.5)──RZ(3.14)──RY(1.57)──╰Z──RZ(3.14)──RY(1.57)──╭C──────────────────────│───────────────────────┤
 2: ──RX(0.6)──RZ(3.14)──RY(1.57)──────────────────────────╰Z──RZ(3.14)──RY(1.57)──╰C──────────────────────┤

Given an operator of the form :math:U=e^{iHt}, where :math:H has commuting terms and known eigenvalues, qml.gradients.generate_shift_rule computes the generalized parameter shift rules for determining the gradient of the expectation value :math:f(t) = \langle 0|U(t)^\dagger \hat{O} U(t)|0\rangle on hardware. (#1788) (#1932)

Given $H = \sum_i a_i h_i$, where the eigenvalues of :math:H are known and all :math:h_i commute, we can compute the frequencies (the unique positive differences of any two eigenvalues) using qml.gradients.eigvals_to_frequencies.

qml.gradients.generate_shift_rule can then be used to compute the parameter shift rules to compute :math:f'(t) using 2R shifted cost function evaluations. This becomes cheaper than the standard application of the chain rule and two-term shift rule when R is less than the number of Pauli words in the generator.

For example, consider the case where :math:H has eigenspectrum (-1, 0, 1):
```
>>> frequencies = qml.gradients.eigvals_to_frequencies((-1, 0, 1))
>>> frequencies
(1, 2)
>>> coeffs, shifts = qml.gradients.generate_shift_rule(frequencies)
>>> coeffs
array([ 0.85355339, -0.85355339, -0.14644661,  0.14644661])
>>> shifts
array([ 0.78539816, -0.78539816,  2.35619449, -2.35619449])
```
As we can see, generate_shift_rule returns four coefficients :math:c_i and shifts :math:s_i corresponding to a four term parameter shift rule. The gradient can then be reconstructed via:

.. math:: \frac{\partial}{\partial\phi}f = \sum_{i} c_i f(\phi + s_i),

where :math:f(\phi) = \langle 0|U(\phi)^\dagger \hat{O} U(\phi)|0\rangle for some observable :math:\hat{O} and the unitary :math:U(\phi)=e^{iH\phi}.

Support for TensorFlow AutoGraph mode with quantum hardware

It is now possible to use TensorFlow's AutoGraph
mode with QNodes on all devices and with arbitrary
differentiation methods. Previously, AutoGraph mode only support `di...

Assets 2

25 Nov 06:56

antalszava

v0.19.1

7d9024b

Release 0.19.1

Bug fixes

Fixes several bugs when using parametric operations with the default.qubit.torch device on GPU. The device takes the torch_device argument once again to allow running non-parametric QNodes on the GPU. (#1927)
Fixes a bug where using JAX's jit function on certain QNodes that contain the qml.QubitStateVector operation raised an error with earlier JAX versions (e.g., jax==0.2.10 and jaxlib==0.1.64). (#1924)

Contributors

This release contains contributions from (in alphabetical order):

Josh Izaac, Christina Lee, Romain Moyard, Lee James O'Riordan, Antal Száva.

Assets 2

09 Nov 05:24

antalszava

v0.19.0

a087aab

Release 0.19.0

New features since last release

Differentiable Hartree-Fock solver

A differentiable Hartree-Fock (HF) solver has been added. It can be used to construct molecular Hamiltonians that can be differentiated with respect to nuclear coordinates and basis-set parameters. (#1610)

The HF solver computes the integrals over basis functions, constructs the relevant matrices, and performs self-consistent-field iterations to obtain a set of optimized molecular orbital coefficients. These coefficients and the computed integrals over basis functions are used to construct the one- and two-body electron integrals in the molecular orbital basis which can be used to generate a differentiable second-quantized Hamiltonian in the fermionic and qubit basis.

The following code shows the construction of the Hamiltonian for the hydrogen molecule where the geometry of the molecule is differentiable.

symbols = ["H", "H"]
geometry = np.array([[0.0000000000, 0.0000000000, -0.6943528941],
                     [0.0000000000, 0.0000000000,  0.6943528941]], requires_grad=True)

mol = qml.hf.Molecule(symbols, geometry)
args_mol = [geometry]

hamiltonian = qml.hf.generate_hamiltonian(mol)(*args_mol)

>>> hamiltonian.coeffs
tensor([-0.09041082+0.j,  0.17220382+0.j,  0.17220382+0.j,
         0.16893367+0.j,  0.04523101+0.j, -0.04523101+0.j,
        -0.04523101+0.j,  0.04523101+0.j, -0.22581352+0.j,
         0.12092003+0.j, -0.22581352+0.j,  0.16615103+0.j,
         0.16615103+0.j,  0.12092003+0.j,  0.17464937+0.j], requires_grad=True)

The generated Hamiltonian can be used in a circuit where the atomic coordinates and circuit parameters are optimized simultaneously.

symbols = ["H", "H"]
geometry = np.array([[0.0000000000, 0.0000000000, 0.0],
                     [0.0000000000, 0.0000000000, 2.0]], requires_grad=True)

mol = qml.hf.Molecule(symbols, geometry)

dev = qml.device("default.qubit", wires=4)
params = [np.array([0.0], requires_grad=True)]

def generate_circuit(mol):
    @qml.qnode(dev)
    def circuit(*args):
        qml.BasisState(np.array([1, 1, 0, 0]), wires=[0, 1, 2, 3])
        qml.DoubleExcitation(*args[0][0], wires=[0, 1, 2, 3])
        return qml.expval(qml.hf.generate_hamiltonian(mol)(*args[1:]))
    return circuit

for n in range(25):

    mol = qml.hf.Molecule(symbols, geometry)
    args = [params, geometry] # initial values of the differentiable parameters

    g_params = qml.grad(generate_circuit(mol), argnum = 0)(*args)
    params = params - 0.5 * g_params[0]

    forces = qml.grad(generate_circuit(mol), argnum = 1)(*args)
    geometry = geometry - 0.5 * forces

    print(f'Step: {n}, Energy: {generate_circuit(mol)(*args)}, Maximum Force: {forces.max()}')

In addition, the new Hartree-Fock solver can further be used to optimize the basis set parameters. For details, please refer to the differentiable Hartree-Fock solver documentation.

Integration with Mitiq

Error mitigation using the zero-noise extrapolation method is now available through the transforms.mitigate_with_zne transform. This transform can integrate with the Mitiq package for unitary folding and extrapolation functionality. (#1813)

Consider the following noisy device:

noise_strength = 0.05
dev = qml.device("default.mixed", wires=2)
dev = qml.transforms.insert(qml.AmplitudeDamping, noise_strength)(dev)

We can mitigate the effects of this noise for circuits run on this device by using the added
transform:

from mitiq.zne.scaling import fold_global
from mitiq.zne.inference import RichardsonFactory

n_wires = 2
n_layers = 2

shapes = qml.SimplifiedTwoDesign.shape(n_wires, n_layers)
np.random.seed(0)
w1, w2 = [np.random.random(s) for s in shapes]

@qml.transforms.mitigate_with_zne([1, 2, 3], fold_global, RichardsonFactory.extrapolate)
@qml.beta.qnode(dev)
def circuit(w1, w2):
    qml.SimplifiedTwoDesign(w1, w2, wires=range(2))
    return qml.expval(qml.PauliZ(0))

Now, when we execute circuit, errors will be automatically mitigated:

>>> circuit(w1, w2)
0.19113067083636542

Powerful new transforms

The unitary matrix corresponding to a quantum circuit can now be generated using the new get_unitary_matrix() transform. (#1609) (#1786)

This transform is fully differentiable across all supported PennyLane autodiff frameworks.

def circuit(theta):
    qml.RX(theta, wires=1)
    qml.PauliZ(wires=0)
    qml.CNOT(wires=[0, 1])

>>> theta = torch.tensor(0.3, requires_grad=True)
>>> matrix = qml.transforms.get_unitary_matrix(circuit)(theta)
>>> print(matrix)
tensor([[ 0.9888+0.0000j,  0.0000+0.0000j,  0.0000-0.1494j,  0.0000+0.0000j],
      [ 0.0000+0.0000j,  0.0000+0.1494j,  0.0000+0.0000j, -0.9888+0.0000j],
      [ 0.0000-0.1494j,  0.0000+0.0000j,  0.9888+0.0000j,  0.0000+0.0000j],
      [ 0.0000+0.0000j, -0.9888+0.0000j,  0.0000+0.0000j,  0.0000+0.1494j]],
     grad_fn=<MmBackward>)
>>> loss = torch.real(torch.trace(matrix))
>>> loss.backward()
>>> theta.grad
tensor(-0.1494)

Arbitrary two-qubit unitaries can now be decomposed into elementary gates. This functionality has been incorporated into the qml.transforms.unitary_to_rot transform, and is available separately as qml.transforms.two_qubit_decomposition. (#1552)

As an example, consider the following randomly-generated matrix and circuit that uses it:

U = np.array([
    [-0.03053706-0.03662692j,  0.01313778+0.38162226j, 0.4101526 -0.81893687j, -0.03864617+0.10743148j],
    [-0.17171136-0.24851809j,  0.06046239+0.1929145j, -0.04813084-0.01748555j, -0.29544883-0.88202604j],
    [ 0.39634931-0.78959795j, -0.25521689-0.17045233j, -0.1391033 -0.09670952j, -0.25043606+0.18393466j],
    [ 0.29599198-0.19573188j,  0.55605806+0.64025769j, 0.06140516+0.35499559j,  0.02674726+0.1563311j ]
])

dev = qml.device('default.qubit', wires=2)

@qml.qnode(dev)
@qml.transforms.unitary_to_rot
def circuit(x, y):
    qml.QubitUnitary(U, wires=[0, 1])
    return qml.expval(qml.PauliZ(wires=0))

If we run the circuit, we can see the new decomposition:

>>> circuit(0.3, 0.4)
tensor(-0.81295986, requires_grad=True)
>>> print(qml.draw(circuit)(0.3, 0.4))
0: ──Rot(2.78, 0.242, -2.28)──╭X──RZ(0.176)───╭C─────────────╭X──Rot(-3.87, 0.321, -2.09)──┤ ⟨Z⟩
1: ──Rot(4.64, 2.69, -1.56)───╰C──RY(-0.883)──╰X──RY(-1.47)──╰C──Rot(1.68, 0.337, 0.587)───┤

A new transform, @qml.batch_params, has been added, that makes QNodes handle a batch dimension in trainable parameters. (#1710) (#1761)

This transform will create multiple circuits, one per batch dimension. As a result, it is both simulator and hardware compatible.

@qml.batch_params
@qml.beta.qnode(dev)
def circuit(x, weights):
    qml.RX(x, wires=0)
    qml.RY(0.2, wires=1)
    qml.templates.StronglyEntanglingLayers(weights, wires=[0, 1, 2])
    return qml.expval(qml.Hadamard(0))

The qml.batch_params decorator allows us to pass arguments x and weights that have a batch dimension. For example,

>>> batch_size = 3
>>> x = np.linspace(0.1, 0.5, batch_size)
>>> weights = np.random.random((batch_size, 10, 3, 3))

If we evaluate the QNode with these inputs, we will get an output of shape (batch_size,):

>>> circuit(x, weights)
tensor([0.08569816, 0.12619101, 0.21122004], requires_grad=True)

The insert transform has now been added, providing a way to insert single-qubit operations into a quantum circuit. The transform can apply to quantum functions, tapes, and devices. (#1795)

The following QNode can be transformed to add noise to the circuit:

dev = qml.device("default.mixed", wires=2)

@qml.qnode(dev)
@qml.transforms.insert(qml.AmplitudeDamping, 0.2, position="end")
def f(w, x, y, z):
    qml.RX(w, wires=0)
    qml.RY(x, wires=1)
    qml.CNOT(wires=[0, 1])
    qml.RY(y, wires=0)
    qml.RX(z, wires=1)
    return qml.expval(qml.PauliZ(0) @ qml.PauliZ(1))

Executions of this circuit will differ from the noise-free value:

>>> f(0.9, 0.4, 0.5, 0.6)
tensor(0.754847, requires_grad=True)
>>> print(qml.draw(f)(0.9, 0.4, 0.5, 0.6))
 0: ──RX(0.9)──╭C──RY(0.5)──AmplitudeDamping(0.2)──╭┤ ⟨Z ⊗ Z⟩
 1: ──RY(0.4)──╰X──RX(0.6)──AmplitudeDamping(0.2)──╰┤ ⟨Z ⊗ Z⟩

Common tape expansion functions are now available in qml.transforms, alongside a new create_expand_fn function for easily creating expansion functions from stopping criteria. (#1734) (#1760)

create_expand_fn takes the default depth to which the expansion function should expand a tape, a stopping criterion, an optional device, and a docstring to be set for the created function. The stopping criterion must take a q...

Assets 2

01 Nov 06:09

josh146

v0.18.0-post2

aaeedb8

Release 0.18.0-post2

A minor post-release to update the PennyLane documentation navigation bar.

Assets 2

25 Sep 07:29

josh146

v0.18.0-post1

82001d0

Release 0.18.0-post1

A minor post-release to update the PennyLane documentation navigation bar to include a link to the demonstrations.

Assets 2

21 Sep 08:02

antalszava

v0.18.0

3d17a45

Release 0.18.0

New features since last release

PennyLane now comes packaged with `lightning.qubit`

The C++-based lightning.qubit device is now included with installations of PennyLane. (#1663)

The lightning.qubit device is a fast state-vector simulator equipped with the efficient adjoint method for differentiating quantum circuits, check out the plugin release notes for more details! The device can be accessed in the following way:

import pennylane as qml

wires = 3
layers = 2
dev = qml.device("lightning.qubit", wires=wires)

@qml.qnode(dev, diff_method="adjoint")
def circuit(weights):
    qml.templates.StronglyEntanglingLayers(weights, wires=range(wires))
    return qml.expval(qml.PauliZ(0))

weights = qml.init.strong_ent_layers_normal(layers, wires, seed=1967)

Evaluating circuits and their gradients on the device can be achieved using the standard approach:

>>> print(f"Circuit evaluated: {circuit(weights)}")
Circuit evaluated: 0.9801286266677633
>>> print(f"Circuit gradient:\n{qml.grad(circuit)(weights)}")
Circuit gradient:
[[[-9.35301749e-17 -1.63051504e-01 -4.14810501e-04]
  [-7.88816484e-17 -1.50136528e-04 -1.77922957e-04]
  [-5.20670796e-17 -3.92874550e-02  8.14523075e-05]]

 [[-1.14472273e-04  3.85963953e-02 -9.39190132e-18]
  [-5.76791765e-05 -9.78478343e-02  0.00000000e+00]
  [ 0.00000000e+00  0.00000000e+00  0.00000000e+00]]]

The adjoint method operates after a forward pass by iteratively applying inverse gates to scan backwards through the circuit. The method is already available in PennyLane's default.qubit device, but the version provided by lightning.qubit integrates with the C++ backend and is more performant, as shown in the plot below: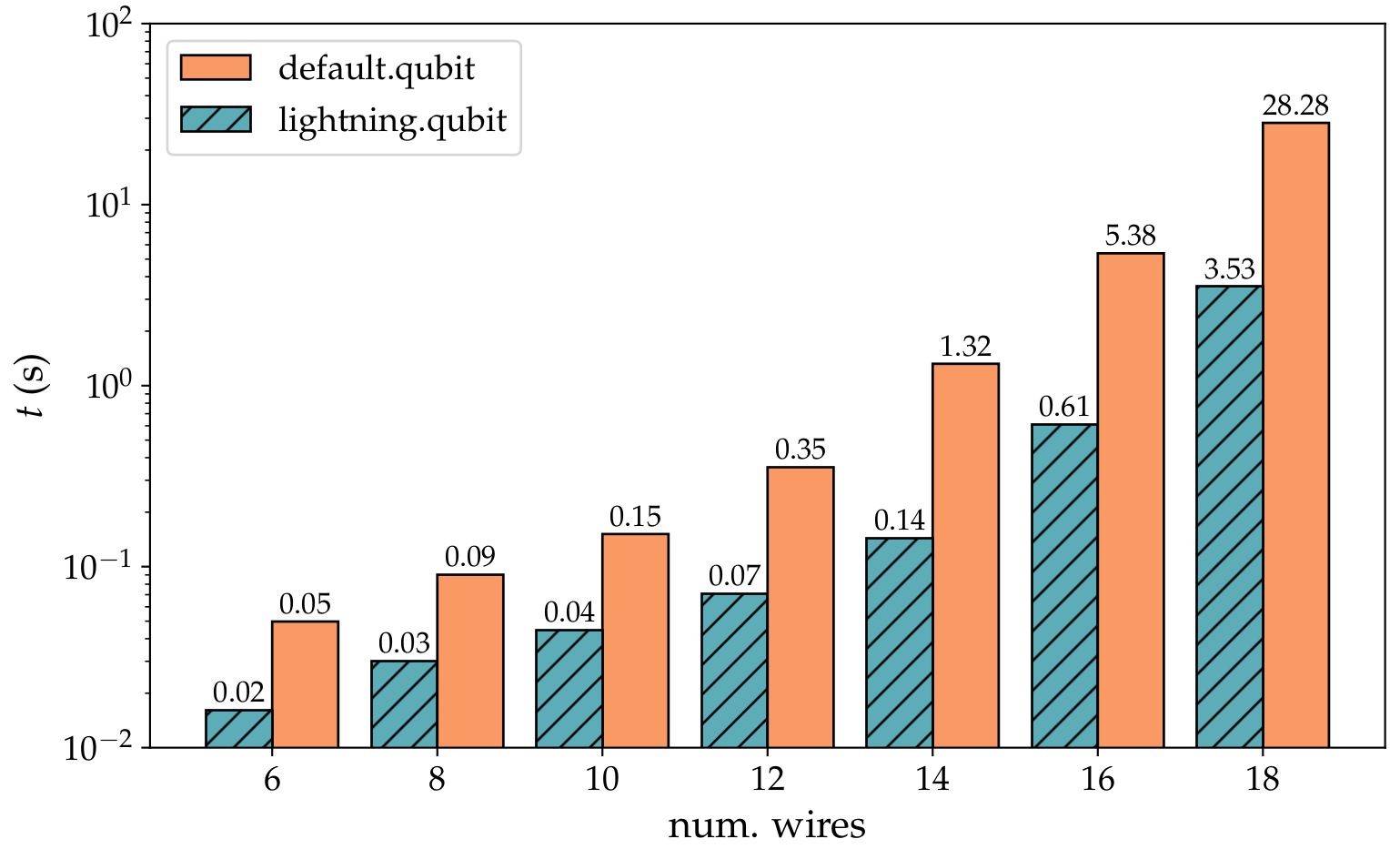

Support for native backpropagation using PyTorch

The built-in PennyLane simulator default.qubit now supports backpropogation with PyTorch. (#1360) (#1598)

As a result, default.qubit can now use end-to-end classical backpropagation as a means to compute gradients. End-to-end backpropagation can be faster than the parameter-shift rule for computing quantum gradients when the number of parameters to be optimized is large. This is now the default differentiation method when using default.qubit with PyTorch.

Using this method, the created QNode is a 'white-box' that is tightly integrated with your PyTorch computation, including TorchScript and GPU support.

x = torch.tensor(0.43316321, dtype=torch.float64, requires_grad=True)
y = torch.tensor(0.2162158, dtype=torch.float64, requires_grad=True)
z = torch.tensor(0.75110998, dtype=torch.float64, requires_grad=True)

p = torch.tensor([x, y, z], requires_grad=True)
dev = qml.device("default.qubit", wires=1)

@qml.qnode(dev, interface="torch", diff_method="backprop")
def circuit(x):
    qml.Rot(x[0], x[1], x[2], wires=0)
    return qml.expval(qml.PauliZ(0))

res = circuit(p)
res.backward()

>>> res = circuit(p)
>>> res.backward()
>>> print(p.grad)
tensor([-9.1798e-17, -2.1454e-01, -1.0511e-16], dtype=torch.float64)

Improved quantum optimization methods

The RotosolveOptimizer now can tackle general parametrized circuits, and is no longer restricted to single-qubit Pauli rotations. (#1489)

This includes:

layers of gates controlled by the same parameter,
controlled variants of parametrized gates, and
Hamiltonian time evolution.

Note that the eigenvalue spectrum of the gate generator needs to be known to use RotosolveOptimizer for a general gate, and it is required to produce equidistant frequencies. For details see Vidal and Theis, 2018 and Wierichs, Izaac, Wang, Lin 2021.

Consider a circuit with a mixture of Pauli rotation gates, controlled Pauli rotations, and single-parameter layers of Pauli rotations:

dev = qml.device('default.qubit', wires=3, shots=None)

@qml.qnode(dev)
def cost_function(rot_param, layer_par, crot_param):
    for i, par in enumerate(rot_param):
        qml.RX(par, wires=i)
    for w in dev.wires:
        qml.RX(layer_par, wires=w)
    for i, par in enumerate(crot_param):
        qml.CRY(par, wires=[i, (i+1) % 3])

    return qml.expval(qml.PauliZ(0) @ qml.PauliZ(1) @ qml.PauliZ(2))

This cost function has one frequency for each of the first RX rotation angles, three frequencies for the layer of RX gates that depend on layer_par, and two frequencies for each of the CRY gate parameters. Rotosolve can then be used to minimize the cost_function:

# Initial parameters
init_param = [
    np.array([0.3, 0.2, 0.67], requires_grad=True),
    np.array(1.1, requires_grad=True),
    np.array([-0.2, 0.1, -2.5], requires_grad=True),
]
# Numbers of frequencies per parameter
num_freqs = [[1, 1, 1], 3, [2, 2, 2]]

opt = qml.RotosolveOptimizer()
param = init_param.copy()

In addition, the optimization technique for the Rotosolve substeps can be chosen via the optimizer and optimizer_kwargs keyword arguments and the minimized cost of the intermediate univariate reconstructions can be read out via full_output, including the cost after the full Rotosolve step:

for step in range(3):
    param, cost, sub_cost = opt.step_and_cost(
        cost_function,
        *param,
        num_freqs=num_freqs,
        full_output=True,
        optimizer="brute",
    )
    print(f"Cost before step: {cost}")
    print(f"Minimization substeps: {np.round(sub_cost, 6)}")

Cost before step: 0.042008210392535605
Minimization substeps: [-0.230905 -0.863336 -0.980072 -0.980072 -1.       -1.       -1.      ]
Cost before step: -0.999999999068121
Minimization substeps: [-1. -1. -1. -1. -1. -1. -1.]
Cost before step: -1.0
Minimization substeps: [-1. -1. -1. -1. -1. -1. -1.]

For usage details please consider the docstring of the optimizer.

Faster, trainable, Hamiltonian simulations

Hamiltonians are now trainable with respect to their coefficients. (#1483)

from pennylane import numpy as np

dev = qml.device("default.qubit", wires=2)
@qml.qnode(dev)
def circuit(coeffs, param):
    qml.RX(param, wires=0)
    qml.RY(param, wires=0)
    return qml.expval(
        qml.Hamiltonian(coeffs, [qml.PauliX(0), qml.PauliZ(0)], simplify=True)
    )

coeffs = np.array([-0.05, 0.17])
param = np.array(1.7)
grad_fn = qml.grad(circuit)

>>> grad_fn(coeffs, param)
(array([-0.12777055,  0.0166009 ]), array(0.0917819))

Furthermore, a gradient recipe for Hamiltonian coefficients has been added. This makes it possible to compute parameter-shift gradients of these coefficients on devices that natively support Hamiltonians. (#1551)

Hamiltonians are now natively supported on the default.qubit device if shots=None. This makes VQE workflows a lot faster in some cases. (#1551) (#1596)
The Hamiltonian can now store grouping information, which can be accessed by a device to speed up computations of the expectation value of a Hamiltonian. (#1515)
```
obs = [qml.PauliX(0), qml.PauliX(1), qml.PauliZ(0)]
coeffs = np.array([1., 2., 3.])
H = qml.Hamiltonian(coeffs, obs, grouping_type='qwc')
```
Initialization with a grouping_type other than None stores the indices
required to make groups of commuting observables and their coefficients.
```
>>> H.grouping_indices
[[0, 1], [2]]
```

Create multi-circuit quantum transforms and custom gradient rules

Custom gradient transforms can now be created using the new @qml.gradients.gradient_transform decorator on a batch-tape transform. (#1589)

Quantum gradient transforms are a specific case of qml.batch_transform.

Supported gradient transforms must be of the following form:
```
@qml.gradients.gradient_transform
def my_custom_gradient(tape, argnum=None, **kwargs):
    ...
    return gradient_tapes, processing_fn
```
Various built-in quantum gradient transforms are provided within the qml.gradients module, including qml.gradients.param_shift. Once defined, quantum gradient transforms can be applied directly to QNodes:
```
>>> @qml.qnode(dev)
... def circuit(x):
...     qml.RX(x, wires=0)
...     qml.CNOT(wires=[0, 1])
...     return qml.expval(qml.PauliZ(0))
>>> circuit(0.3)
tensor(0.95533649, requires_grad=True)
>>> qml.gradients.param_shift(circui...
```

Assets 2

17 Aug 02:19

antalszava

v0.17.0

74620a9

Release 0.17.0

New features since the last release

Circuit optimization

PennyLane can now perform quantum circuit optimization using the top-level transform qml.compile. The compile transform allows you to chain together sequences of tape and quantum function transforms into custom circuit optimization pipelines. (#1475)

For example, take the following decorated quantum function:

dev = qml.device('default.qubit', wires=[0, 1, 2])

@qml.qnode(dev)
@qml.compile()
def qfunc(x, y, z):
    qml.Hadamard(wires=0)
    qml.Hadamard(wires=1)
    qml.Hadamard(wires=2)
    qml.RZ(z, wires=2)
    qml.CNOT(wires=[2, 1])
    qml.RX(z, wires=0)
    qml.CNOT(wires=[1, 0])
    qml.RX(x, wires=0)
    qml.CNOT(wires=[1, 0])
    qml.RZ(-z, wires=2)
    qml.RX(y, wires=2)
    qml.PauliY(wires=2)
    qml.CZ(wires=[1, 2])
    return qml.expval(qml.PauliZ(wires=0))

The default behaviour of qml.compile is to apply a sequence of three transforms: commute_controlled, cancel_inverses, and then merge_rotations.

>>> print(qml.draw(qfunc)(0.2, 0.3, 0.4))
 0: ──H───RX(0.6)──────────────────┤ ⟨Z⟩
 1: ──H──╭X────────────────────╭C──┤
 2: ──H──╰C────────RX(0.3)──Y──╰Z──┤

The qml.compile transform is flexible and accepts a custom pipeline of tape and quantum function transforms (you can even write your own!). For example, if we wanted to only push single-qubit gates through controlled gates and cancel adjacent inverses, we could do:

from pennylane.transforms import commute_controlled, cancel_inverses
pipeline = [commute_controlled, cancel_inverses]

@qml.qnode(dev)
@qml.compile(pipeline=pipeline)
def qfunc(x, y, z):
    qml.Hadamard(wires=0)
    qml.Hadamard(wires=1)
    qml.Hadamard(wires=2)
    qml.RZ(z, wires=2)
    qml.CNOT(wires=[2, 1])
    qml.RX(z, wires=0)
    qml.CNOT(wires=[1, 0])
    qml.RX(x, wires=0)
    qml.CNOT(wires=[1, 0])
    qml.RZ(-z, wires=2)
    qml.RX(y, wires=2)
    qml.PauliY(wires=2)
    qml.CZ(wires=[1, 2])
    return qml.expval(qml.PauliZ(wires=0))

>>> print(qml.draw(qfunc)(0.2, 0.3, 0.4))
 0: ──H───RX(0.4)──RX(0.2)────────────────────────────┤ ⟨Z⟩
 1: ──H──╭X───────────────────────────────────────╭C──┤
 2: ──H──╰C────────RZ(0.4)──RZ(-0.4)──RX(0.3)──Y──╰Z──┤

The following compilation transforms have been added and are also available to use, either independently, or within a qml.compile pipeline:

commute_controlled: push commuting single-qubit gates through controlled operations. (#1464)
cancel_inverses: removes adjacent pairs of operations that cancel out. (#1455)
merge_rotations: combines adjacent rotation gates of the same type into a single gate, including controlled rotations. (#1455)
single_qubit_fusion: acts on all sequences of single-qubit operations in a quantum function, and converts each sequence to a single Rot gate. (#1458)

For more details on qml.compile and the available compilation transforms, see the compilation documentation.

QNodes are even more powerful

Computational basis samples directly from the underlying device can now be returned directly from QNodes via qml.sample(). (#1441)

dev = qml.device("default.qubit", wires=3, shots=5)

@qml.qnode(dev)
def circuit_1():
    qml.Hadamard(wires=0)
    qml.Hadamard(wires=1)
    return qml.sample()

@qml.qnode(dev)
def circuit_2():
    qml.Hadamard(wires=0)
    qml.Hadamard(wires=1)
    return qml.sample(wires=[0,2])    # no observable provided and wires specified

>>> print(circuit_1())
[[1, 0, 0],
 [1, 1, 0],
 [1, 0, 0],
 [0, 0, 0],
 [0, 1, 0]]

>>> print(circuit_2())
[[1, 0],
 [1, 0],
 [1, 0],
 [0, 0],
 [0, 0]]

>>> print(qml.draw(circuit_2)())
 0: ──H──╭┤ Sample[basis]
 1: ──H──│┤
 2: ─────╰┤ Sample[basis]

The new qml.apply function can be used to add operations that might have already been instantiated elsewhere to the QNode and other queuing contexts: (#1433)

op = qml.RX(0.4, wires=0)
dev = qml.device("default.qubit", wires=2)

@qml.qnode(dev)
def circuit(x):
    qml.RY(x, wires=0)
    qml.apply(op)
    return qml.expval(qml.PauliZ(0))

>>> print(qml.draw(circuit)(0.6))
0: ──RY(0.6)──RX(0.4)──┤ ⟨Z⟩

Previously instantiated measurements can also be applied to QNodes.

Device Resource Tracker

The new Device Tracker capabilities allows for flexible and versatile tracking of executions, even inside parameter-shift gradients. This functionality will improve the ease of monitoring large batches and remote jobs. (#1355)

dev = qml.device('default.qubit', wires=1, shots=100)

@qml.qnode(dev, diff_method="parameter-shift")
def circuit(x):
    qml.RX(x, wires=0)
    return qml.expval(qml.PauliZ(0))

x = np.array(0.1)

with qml.Tracker(circuit.device) as tracker:
    qml.grad(circuit)(x)

>>> tracker.totals
{'executions': 3, 'shots': 300, 'batches': 1, 'batch_len': 2}
>>> tracker.history
{'executions': [1, 1, 1],
 'shots': [100, 100, 100],
 'batches': [1],
 'batch_len': [2]}
>>> tracker.latest
{'batches': 1, 'batch_len': 2}

Users can also provide a custom function to the callback keyword that gets called each time the information is updated. This functionality allows users to monitor remote jobs or large parameter-shift batches.

>>> def shots_info(totals, history, latest):
...     print("Total shots: ", totals['shots'])
>>> with qml.Tracker(circuit.device, callback=shots_info) as tracker:
...     qml.grad(circuit)(0.1)
Total shots:  100
Total shots:  200
Total shots:  300
Total shots:  300

Containerization support

Docker support for building PennyLane with support for all interfaces (TensorFlow, Torch, and Jax), as well as device plugins and QChem, for GPUs and CPUs, has been added. (#1391)

The build process using Docker and make requires that the repository source code is cloned or downloaded from GitHub. Visit the the detailed description for an extended list of options.

Improved Hamiltonian simulations

Added a sparse Hamiltonian observable and the functionality to support computing its expectation value with default.qubit. (#1398)

For example, the following QNode returns the expectation value of a sparse Hamiltonian:
```
dev = qml.device("default.qubit", wires=2)

@qml.qnode(dev, diff_method="parameter-shift")
def circuit(param, H):
    qml.PauliX(0)
    qml.SingleExcitation(param, wires=[0, 1])
    return qml.expval(qml.SparseHamiltonian(H, [0, 1]))
```
We can execute this QNode, passing in a sparse identity matrix:
```
>>> print(circuit([0.5], scipy.sparse.eye(4).tocoo()))
0.9999999999999999
```
The expectation value of the sparse Hamiltonian is computed directly, which leads to executions that are faster by orders of magnitude. Note that "parameter-shift" is the only differentiation method that is currently supported when the observable is a sparse Hamiltonian.

VQE problems can now be intuitively set up by passing the Hamiltonian as an observable. (#1474)

dev = qml.device("default.qubit", wires=2)
H = qml.Hamiltonian([1., 2., 3.],  [qml.PauliZ(0), qml.PauliY(0), qml.PauliZ(1)])
w = qml.init.strong_ent_layers_uniform(1, 2, seed=1967)

@qml.qnode(dev)
def circuit(w):
    qml.templates.StronglyEntanglingLayers(w, wires=range(2))
    return qml.expval(H)

>>> print(circuit(w))
-1.5133943637878295
>>> print(qml.grad(circuit)(w))
[[[-8.32667268e-17  1.39122955e+00 -9.12462052e-02]
[ 1.02348685e-16 -7.77143238e-01 -1.74708049e-01]]]

Note that other measurement types like var(H) or sample(H), as well as multiple expectations like expval(H1), expval(H2) are not supported.

Added functionality to compute the sparse matrix representation of a qml.Hamiltonian object. (#1394)

New gradients module

A new gradients module qml.gradients has been added, which provides differentiable quantum gradient transforms. (#1476) (#1479) (#1486)

Available quantum gradient transforms include:
- qml.gradients.finite_diff
- qml.gradients.param_shift
- qml.gradients.param_shift_cv
For example,
```
>>> params = np.array([0.3,0.4,0.5], requires_grad=True)
>>> with qml.tape.JacobianTape() as tape:
...     qml.RX(params[0], wires=0)
...     qml.RY(params[1], wires=0)
...     qml.RX(params[2], wires=0)
...   ...
```

Assets 2

22 Jun 01:40

antalszava

v0.16.0

8d1e245

Release 0.16.0

New features since last release

First class support for quantum kernels

The new qml.kernels module provides basic functionalities for working with quantum kernels as well as post-processing methods to mitigate sampling errors and device noise: (#1102)

num_wires = 6
wires = range(num_wires)
dev = qml.device('default.qubit', wires=wires)

@qml.qnode(dev)
def kernel_circuit(x1, x2):
    qml.templates.AngleEmbedding(x1, wires=wires)
    qml.adjoint(qml.templates.AngleEmbedding)(x2, wires=wires)
    return qml.probs(wires)

kernel = lambda x1, x2: kernel_circuit(x1, x2)[0]
X_train = np.random.random((10, 6))
X_test = np.random.random((5, 6))

# Create symmetric square kernel matrix (for training)
K = qml.kernels.square_kernel_matrix(X_train, kernel)

# Compute kernel between test and training data.
K_test = qml.kernels.kernel_matrix(X_train, X_test, kernel)
K1 = qml.kernels.mitigate_depolarizing_noise(K, num_wires, method='single')

Extract the fourier representation of quantum circuits

PennyLane now has a fourier module, which hosts a growing library of methods that help with investigating the Fourier representation of functions implemented by quantum circuits. The Fourier representation can be used to examine and characterize the expressivity of the quantum circuit. (#1160) (#1378)

For example, one can plot distributions over Fourier series coefficients like this one:

Seamless support for working with the Pauli group

Added functionality for constructing and manipulating the Pauli group (#1181).

The function qml.grouping.pauli_group provides a generator to easily loop over the group, or construct and store it in its entirety. For example, we can construct the single-qubit Pauli group like so:

>>> from pennylane.grouping import pauli_group
>>> pauli_group_1_qubit = list(pauli_group(1))
>>> pauli_group_1_qubit
[Identity(wires=[0]), PauliZ(wires=[0]), PauliX(wires=[0]), PauliY(wires=[0])]

We can multiply together its members at the level of Pauli words using the pauli_mult and pauli_multi_with_phase functions. This can be done on arbitrarily-labeled wires as well, by defining a wire map.

>>> from pennylane.grouping import pauli_group, pauli_mult
>>> wire_map = {'a' : 0, 'b' : 1, 'c' : 2}
>>> pg = list(pauli_group(3, wire_map=wire_map))
>>> pg[3]
PauliZ(wires=['b']) @ PauliZ(wires=['c'])
>>> pg[55]
PauliY(wires=['a']) @ PauliY(wires=['b']) @ PauliZ(wires=['c'])
>>> pauli_mult(pg[3], pg[55], wire_map=wire_map)
PauliY(wires=['a']) @ PauliX(wires=['b'])

Functions for conversion of Pauli observables to strings (and back) are included.

>>> from pennylane.grouping import pauli_word_to_string, string_to_pauli_word
>>> pauli_word_to_string(pg[55], wire_map=wire_map)
'YYZ'
>>> string_to_pauli_word('ZXY', wire_map=wire_map)
PauliZ(wires=['a']) @ PauliX(wires=['b']) @ PauliY(wires=['c'])

Calculation of the matrix representation for arbitrary Paulis and wire maps is now also supported.

>>> from pennylane.grouping import pauli_word_to_matrix
>>> wire_map = {'a' : 0, 'b' : 1}
>>> pauli_word = qml.PauliZ('b')  # corresponds to Pauli 'IZ'
>>> pauli_word_to_matrix(pauli_word, wire_map=wire_map)
array([[ 1.,  0.,  0.,  0.],
       [ 0., -1.,  0., -0.],
       [ 0.,  0.,  1.,  0.],
       [ 0., -0.,  0., -1.]])

New transforms

The qml.specs QNode transform creates a function that returns specifications or details about the QNode, including depth, number of gates, and number of gradient executions required. (#1245)

For example:

dev = qml.device('default.qubit', wires=4)

@qml.qnode(dev, diff_method='parameter-shift')
def circuit(x, y):
    qml.RX(x[0], wires=0)
    qml.Toffoli(wires=(0, 1, 2))
    qml.CRY(x[1], wires=(0, 1))
    qml.Rot(x[2], x[3], y, wires=0)
    return qml.expval(qml.PauliZ(0)), qml.expval(qml.PauliX(1))

We can now use the qml.specs transform to generate a function that returns details and resource information:

>>> x = np.array([0.05, 0.1, 0.2, 0.3], requires_grad=True)
>>> y = np.array(0.4, requires_grad=False)
>>> specs_func = qml.specs(circuit)
>>> specs_func(x, y)
{'gate_sizes': defaultdict(int, {1: 2, 3: 1, 2: 1}),
 'gate_types': defaultdict(int, {'RX': 1, 'Toffoli': 1, 'CRY': 1, 'Rot': 1}),
 'num_operations': 4,
 'num_observables': 2,
 'num_diagonalizing_gates': 1,
 'num_used_wires': 3,
 'depth': 4,
 'num_trainable_params': 4,
 'num_parameter_shift_executions': 11,
 'num_device_wires': 4,
 'device_name': 'default.qubit',
 'diff_method': 'parameter-shift'}

The tape methods get_resources and get_depth are superseded by specs and will be deprecated after one release cycle.

Adds a decorator @qml.qfunc_transform to easily create a transformation that modifies the behaviour of a quantum function.
(#1315)

For example, consider the following transform, which scales the parameter of all RX gates by :math:x \rightarrow \sin(a) \sqrt{x}, and the parameters of all RY gates by :math:y \rightarrow \cos(a * b) y:

@qml.qfunc_transform
def my_transform(tape, a, b):
    for op in tape.operations + tape.measurements:
        if op.name == "RX":
            x = op.parameters[0]
            qml.RX(qml.math.sin(a) * qml.math.sqrt(x), wires=op.wires)
        elif op.name == "RY":
            y = op.parameters[0]
            qml.RX(qml.math.cos(a * b) * y, wires=op.wires)
        else:
            op.queue()

We can now apply this transform to any quantum function:

dev = qml.device("default.qubit", wires=2)

def ansatz(x):
    qml.Hadamard(wires=0)
    qml.RX(x[0], wires=0)
    qml.RY(x[1], wires=1)
    qml.CNOT(wires=[0, 1])

@qml.qnode(dev)
def circuit(params, transform_weights):
    qml.RX(0.1, wires=0)

    # apply the transform to the ansatz
    my_transform(*transform_weights)(ansatz)(params)

    return qml.expval(qml.PauliZ(1))

We can print this QNode to show that the qfunc transform is taking place:

>>> x = np.array([0.5, 0.3], requires_grad=True)
>>> transform_weights = np.array([0.1, 0.6], requires_grad=True)
>>> print(qml.draw(circuit)(x, transform_weights))
 0: ──RX(0.1)────H──RX(0.0706)──╭C──┤
 1: ──RX(0.299)─────────────────╰X──┤ ⟨Z⟩

Evaluating the QNode, as well as the derivative, with respect to the gate parameter and the transform weights:

>>> circuit(x, transform_weights)
tensor(0.00672829, requires_grad=True)
>>> qml.grad(circuit)(x, transform_weights)
(array([ 0.00671711, -0.00207359]), array([6.69695008e-02, 3.73694364e-06]))

Adds a hamiltonian_expand tape transform. This takes a tape ending in qml.expval(H), where H is a Hamiltonian, and maps it to a collection of tapes which can be executed and passed into a post-processing function yielding the expectation value. (#1142)

Example use:
```
H = qml.PauliZ(0) + 3 * qml.PauliZ(0) @ qml.PauliX(1)

with qml.tape.QuantumTape() as tape:
    qml.Hadamard(wires=1)
    qml.expval(H)

tapes, fn = qml.transforms.hamiltonian_expand(tape)
```
We can now evaluate the transformed tapes, and apply the post-processing function:
```
>>> dev = qml.device("default.qubit", wires=3)
>>> res = dev.batch_execute(tapes)
>>> fn(res)
3.999999999999999
```

The quantum_monte_carlo transform has been added, allowing an input circuit to be transformed into the full quantum Monte Carlo algorithm. (#1316)

Suppose we want to measure the expectation value of the sine squared function according to a standard normal distribution. We can calculate the expectation value analytically as 0.432332, but we can also estimate using the quantum Monte Carlo algorithm. The first step is to discretize the problem:

from scipy.stats import norm

m = 5
M = 2 ** m

xmax = np.pi  # bound to region [-pi, pi]
xs = np.linspace(-xmax, xmax, M)

probs = np.array([norm().pdf(x) for x in xs])
probs /= np.sum(probs)

func = lambda i: np.sin(xs[i]) ** 2
r_rotations = np.array([2 * np.arcsin(np.sqrt(func(i))) for i in range(M)])

The quantum_monte_carlo transform can then be used:

from pennylane.templates.state_preparations.mottonen import (
    _uniform_rotation_dagger as r_unitary,
)

n = 6
N = 2 ** n

a_wires = range(m)
wires = range(m + 1)
target_wire = m
estimation_wires = range(m + 1, n + m + 1)

dev = qml.device("default.qubit", wires=(n + m + 1))

def fn():
    qml.templates.MottonenStatePreparation(np.sqrt(probs), wires=a_wires)
    r_unitary(qml.RY, r_rotations, control_wires=a_wires[::-1], target_wire=target_wire)

@qml.qnode(dev)
def qmc():
    qml.quantum_monte_carlo(fn, wires, target_wire, estimation_wires)()
    return qml.probs(estimation_wires)...

Assets 2

03 May 08:34

josh146

v0.15.1

53b8d65

Release 0.15.1

Bug fixes

Fixes two bugs in the parameter-shift Hessian. (#1260)
- Fixes a bug where having an unused parameter in the Autograd interface would result in an indexing error during backpropagation.
- The parameter-shift Hessian only supports the two-term parameter-shift rule currently, so raises an error if asked to differentiate any unsupported gates (such as the controlled rotation gates).
A bug which resulted in qml.adjoint() and qml.inv() failing to work with templates has been fixed. (#1243)
Deprecation warning instances in PennyLane have been changed to UserWarning, to account for recent changes to how Python warnings are filtered in PEP565. (#1211)
The version requirement for PySCF has been modified to allow for pyscf>=1.7.2. (#1254)

Documentation

Updated the order of the parameters to the GaussianState operation to match the way that the PennyLane-SF plugin uses them. (#1255)

Contributors

This release contains contributions from (in alphabetical order):

Josh Izaac, Maria Schuld, Antal Száva.

Assets 2

20 Apr 07:06

josh146

v0.15.0

6252d3e

Release 0.15.0

New features since last release

Better and more flexible shot control

Adds a new optimizer qml.ShotAdaptiveOptimizer, a gradient-descent optimizer where the shot rate is adaptively calculated using the variances of the parameter-shift gradient. (#1139)

By keeping a running average of the parameter-shift gradient and the variance of the parameter-shift gradient, this optimizer frugally distributes a shot budget across the partial derivatives of each parameter.

In addition, if computing the expectation value of a Hamiltonian, weighted random sampling can be used to further distribute the shot budget across the local terms from which the Hamiltonian is constructed.

This optimizer is based on both the iCANS1 and Rosalin shot-adaptive optimizers.

Once constructed, the cost function can be passed directly to the optimizer's step method. The attribute opt.total_shots_used can be used to track the number of shots per iteration.

>>> coeffs = [2, 4, -1, 5, 2]
>>> obs = [
...   qml.PauliX(1),
...   qml.PauliZ(1),
...   qml.PauliX(0) @ qml.PauliX(1),
...   qml.PauliY(0) @ qml.PauliY(1),
...   qml.PauliZ(0) @ qml.PauliZ(1)
... ]
>>> H = qml.Hamiltonian(coeffs, obs)
>>> dev = qml.device("default.qubit", wires=2, shots=100)
>>> cost = qml.ExpvalCost(qml.templates.StronglyEntanglingLayers, H, dev)
>>> params = qml.init.strong_ent_layers_uniform(n_layers=2, n_wires=2)
>>> opt = qml.ShotAdaptiveOptimizer(min_shots=10)
>>> for i in range(5):
...    params = opt.step(cost, params)
...    print(f"Step {i}: cost = {cost(params):.2f}, shots_used = {opt.total_shots_used}")
Step 0: cost = -5.68, shots_used = 240
Step 1: cost = -2.98, shots_used = 336
Step 2: cost = -4.97, shots_used = 624
Step 3: cost = -5.53, shots_used = 1054
Step 4: cost = -6.50, shots_used = 1798

Batches of shots can now be specified as a list, allowing measurement statistics to be course-grained with a single QNode evaluation. (#1103)
```
>>> shots_list = [5, 10, 1000]
>>> dev = qml.device("default.qubit", wires=2, shots=shots_list)
```
When QNodes are executed on this device, a single execution of 1015 shots will be submitted. However, three sets of measurement statistics will be returned; using the first 5 shots, second set of 10 shots, and final 1000 shots, separately.

For example, executing a circuit with two outputs will lead to a result of shape (3, 2):
```
>>> @qml.qnode(dev)
... def circuit(x):
...     qml.RX(x, wires=0)
...     qml.CNOT(wires=[0, 1])
...     return qml.expval(qml.PauliZ(0) @ qml.PauliX(1)), qml.expval(qml.PauliZ(0))
>>> circuit(0.5)
[[0.33333333 1.        ]
 [0.2        1.        ]
 [0.012      0.868     ]]
```
This output remains fully differentiable.

The number of shots can now be specified on a per-call basis when evaluating a QNode. (#1075).

For this, the qnode should be called with an additional shots keyword argument:

>>> dev = qml.device('default.qubit', wires=1, shots=10) # default is 10
>>> @qml.qnode(dev)
... def circuit(a):
...     qml.RX(a, wires=0)
...     return qml.sample(qml.PauliZ(wires=0))
>>> circuit(0.8)
[ 1  1  1 -1 -1  1  1  1  1  1]
>>> circuit(0.8, shots=3)
[ 1  1  1]
>>> circuit(0.8)
[ 1  1  1 -1 -1  1  1  1  1  1]

New differentiable quantum transforms

A new module is available, qml.transforms, which contains differentiable quantum transforms. These are functions that act on QNodes, quantum functions, devices, and tapes, transforming them while remaining fully differentiable.

A new adjoint transform has been added. (#1111) (#1135)

This new method allows users to apply the adjoint of an arbitrary sequence of operations.

def subroutine(wire):
    qml.RX(0.123, wires=wire)
    qml.RY(0.456, wires=wire)

dev = qml.device('default.qubit', wires=1)
@qml.qnode(dev)
def circuit():
    subroutine(0)
    qml.adjoint(subroutine)(0)
    return qml.expval(qml.PauliZ(0))

This creates the following circuit:

>>> print(qml.draw(circuit)())
0: --RX(0.123)--RY(0.456)--RY(-0.456)--RX(-0.123)--| <Z>

Directly applying to a gate also works as expected.

qml.adjoint(qml.RX)(0.123, wires=0) # applies RX(-0.123)

A new transform qml.ctrl is now available that adds control wires to subroutines. (#1157)

def my_ansatz(params):
   qml.RX(params[0], wires=0)
   qml.RZ(params[1], wires=1)

# Create a new operation that applies `my_ansatz`
# controlled by the "2" wire.
my_ansatz2 = qml.ctrl(my_ansatz, control=2)

@qml.qnode(dev)
def circuit(params):
    my_ansatz2(params)
    return qml.state()

This is equivalent to:

@qml.qnode(...)
def circuit(params):
    qml.CRX(params[0], wires=[2, 0])
    qml.CRZ(params[1], wires=[2, 1])
    return qml.state()

The qml.transforms.classical_jacobian transform has been added. (#1186)

This transform returns a function to extract the Jacobian matrix of the classical part of a QNode, allowing the classical dependence between the QNode arguments and the quantum gate arguments to be extracted.

For example, given the following QNode:
```
>>> @qml.qnode(dev)
... def circuit(weights):
...     qml.RX(weights[0], wires=0)
...     qml.RY(weights[0], wires=1)
...     qml.RZ(weights[2] ** 2, wires=1)
...     return qml.expval(qml.PauliZ(0))
```
We can use this transform to extract the relationship :math:f: \mathbb{R}^n \rightarrow\mathbb{R}^m between the input QNode arguments :math:w and the gate arguments :math:g, for a given value of the QNode arguments:
```
>>> cjac_fn = qml.transforms.classical_jacobian(circuit)
>>> weights = np.array([1., 1., 1.], requires_grad=True)
>>> cjac = cjac_fn(weights)
>>> print(cjac)
[[1. 0. 0.]
 [1. 0. 0.]
 [0. 0. 2.]]
```
The returned Jacobian has rows corresponding to gate arguments, and columns corresponding to QNode arguments; that is, :math:J_{ij} = \frac{\partial}{\partial g_i} f(w_j).

More operations and templates

Added the SingleExcitation two-qubit operation, which is useful for quantum chemistry applications. (#1121)

It can be used to perform an SO(2) rotation in the subspace spanned by the states :math:|01\rangle and :math:|10\rangle. For example, the following circuit performs the transformation :math:|10\rangle \rightarrow \cos(\phi/2)|10\rangle - \sin(\phi/2)|01\rangle:
```
dev = qml.device('default.qubit', wires=2)

@qml.qnode(dev)
def circuit(phi):
    qml.PauliX(wires=0)
    qml.SingleExcitation(phi, wires=[0, 1])
```
The SingleExcitation operation supports analytic gradients on hardware using only four expectation value calculations, following results from Kottmann et al.
Added the DoubleExcitation four-qubit operation, which is useful for quantum chemistry applications. (#1123)

It can be used to perform an SO(2) rotation in the subspace spanned by the states :math:|1100\rangle and :math:|0011\rangle. For example, the following circuit performs the transformation :math:|1100\rangle\rightarrow \cos(\phi/2)|1100\rangle - \sin(\phi/2)|0011\rangle:
```
dev = qml.device('default.qubit', wires=2)

@qml.qnode(dev)
def circuit(phi):
    qml.PauliX(wires=0)
    qml.PauliX(wires=1)
    qml.DoubleExcitation(phi, wires=[0, 1, 2, 3])
```
The DoubleExcitation operation supports analytic gradients on hardware using only four expectation value calculations, following results from Kottmann et al..

Added the QuantumMonteCarlo template for performing quantum Monte Carlo estimation of an expectation value on simulator. (#1130)

The following example shows how the expectation value of sine squared over a standard normal distribution can be approximated:

from scipy.stats import norm

m = 5
M = 2 ** m
n = 10
N = 2 ** n
target_wires = range(m + 1)
estimation_wires = range(m + 1, n + m + 1)

xmax = np.pi  # bound to region [-pi, pi]
xs = np.linspace(-xmax, xmax, M)

probs = np.array([norm().pdf(x) for x in xs])
probs /= np.sum(probs)

func = lambda i: np.sin(xs[i]) ** 2

dev = qml.device("default.qubit", wires=(n + m + 1))

@qml.qnode(dev)
def circuit():
    qml.templates.QuantumMonteCarlo(
        probs,
        func,
        target_wires=target_wires,
        estimation_wires=estimation_wires,
    )
    return qml.probs(estimation_wires)

phase_estimated = np.argmax(circuit()[:int(N / 2)]) / N
expectation_estimated = (1 - np.cos(np.pi * phase_estimated)) / 2

Added the QuantumPhaseEstimation template for performing quantum phase estimation for an input unitary matrix. (#1095)

Consider the matrix corresponding ...

Assets 2

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

New features since last release

Shiny new circuit drawer!🎨🖌️

New and improved quantum-aware optimizers

Faster performance with optimized quantum workflows

Support for TensorFlow AutoGraph mode with quantum hardware

Bug fixes

Contributors

New features since last release

Differentiable Hartree-Fock solver

Integration with Mitiq

Powerful new transforms

New features since last release

PennyLane now comes packaged with `lightning.qubit`

Support for native backpropagation using PyTorch

Improved quantum optimization methods

Faster, trainable, Hamiltonian simulations

Create multi-circuit quantum transforms and custom gradient rules

New features since the last release

Circuit optimization

QNodes are even more powerful

Device Resource Tracker

Containerization support

Improved Hamiltonian simulations

New gradients module

New features since last release

First class support for quantum kernels

Extract the fourier representation of quantum circuits

Seamless support for working with the Pauli group

New transforms

Bug fixes

Documentation

Contributors

New features since last release

Better and more flexible shot control

New differentiable quantum transforms

More operations and templates

Releases: PennyLaneAI/pennylane

Release 0.20.0

New features since last release

Shiny new circuit drawer!🎨🖌️

New and improved quantum-aware optimizers

Faster performance with optimized quantum workflows

Support for TensorFlow AutoGraph mode with quantum hardware

Release 0.19.1

Bug fixes

Contributors

Release 0.19.0

New features since last release

Differentiable Hartree-Fock solver

Integration with Mitiq

Powerful new transforms

Release 0.18.0-post2

Release 0.18.0-post1

Release 0.18.0

New features since last release

PennyLane now comes packaged with lightning.qubit

Support for native backpropagation using PyTorch

Improved quantum optimization methods

Faster, trainable, Hamiltonian simulations

Create multi-circuit quantum transforms and custom gradient rules

Release 0.17.0

New features since the last release

Circuit optimization

QNodes are even more powerful

Device Resource Tracker

Containerization support

Improved Hamiltonian simulations

New gradients module

Release 0.16.0

New features since last release

First class support for quantum kernels

Extract the fourier representation of quantum circuits

Seamless support for working with the Pauli group

New transforms

Release 0.15.1

Bug fixes

Documentation

Contributors

Release 0.15.0

New features since last release

Better and more flexible shot control

New differentiable quantum transforms

More operations and templates

PennyLane now comes packaged with `lightning.qubit`