-
Notifications
You must be signed in to change notification settings - Fork 182
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Expectation values of Pauli strings? #43
Comments
|
One naive example for the expectance calculation could be from paddle_quantum import Hamiltonian
from paddle_quantum.state import random_state
psi = random_state(2)
pauli_str = [(1.0, 'Z0, Z1'), (2.0, 'X0, Y1')]
H = Hamiltonian(pauli_str)
print("The expectation value of the observable ZZ + 2XY is", psi.expec_val(H))Above example cannot be used in a QNN, in which case you should try from paddle_quantum.loss import ExpecVal
loss_fcn = ExpecVal(H)
print("The loss value is", loss_fcn(psi)) |
|
Thank you very much. %reset -f
import numpy as np
from numpy import pi as PI
import paddle
import paddle_quantum
from paddle import matmul
from paddle_quantum.ansatz import Circuit
from paddle_quantum.qinfo import random_pauli_str_generator, pauli_str_to_matrix
from paddle_quantum.linalg import dagger
from paddle_quantum import Hamiltonian
from paddle_quantum.state import random_state
x0=np.array([1/np.sqrt(2), 1/np.sqrt(2)])
x1=np.array([1,0])
x2=np.array([0,1])
state_lst=(x0,x1,x2)
pauli_str_lst = ([(1.0, 'X0')],[(1.0, 'Y0')],[(1.0, 'Z0')])
for gate in pauli_str_lst:
# print (gate)
H = Hamiltonian(gate)
for state in state_lst:
psi=paddle_quantum.State(paddle.to_tensor(state,dtype='complex64'), dtype='complex64')
print("Gate {}, State {}, Exp-val {}".format(gate, psi, psi.expec_val(H).numpy()))Thanks |
|
Some codes in terms of import numpy as np
import paddle_quantum as pq
from paddle_quantum import Hamiltonian
from paddle_quantum.state import State
pq.set_backend('state_vector')
pq.set_dtype('complex128')
x0 = np.array([1, 1]) / np.sqrt(2)
x1 = np.array([1, 0])
x2 = np.array([0, 1])
state_list = (x0,x1,x2)
pauli_str_list = ([(1.0, 'X0')],[(1.0, 'Y0')],[(1.0, 'Z0')])
for pauli_str in pauli_str_list:
H = Hamiltonian(pauli_str)
for vec in state_list:
psi = State(vec)
print(f"Observable {H.pauli_words}, State {psi.numpy()}, Exp val {psi.expec_val(H)}")You can refer to the API documents of |
|
? |
|
The operation |
|
@imppresser see the example here: |
|
Hi there. The function To calculate from paddle_quantum import Hamiltonian
from paddle_quantum.state import random_state
from paddle_quantum.qinfo import random_pauli_str_generator
num_qubits = 3
psi = random_state(num_qubits)
H = Hamiltonian(random_pauli_str_generator(num_qubits))
H_matrix = paddle.to_tensor(H.construct_h_matrix())
expect_value = psi.bra @ H_matrix @ H_matrix @ psi.ket
print("The pauli string of this Hamiltonian is \n", H.pauli_str)
print("The expectation value is", expect_value.item()) |
Thank you for your detailed lecture note, caculating the H^2 is surely the way. However, in my case need more general way of implementing code of H^2, because the variety of H. Very happy to find the course, it will help a lot! |
Thanks for the detailed feedback. I noticed the "expect_val()" function changed (for compatibility). The solution you give will help me out! |
|
Are you using a GPU? Can I see the a full code snippet? |
Not using GPU. The problem is to construct h_matrix, it is natural cannot build 2^18 x 2^18 complex64 matrix on PC, it will need 500+GB. |
|
You have reached another motivation to use the class Regarding your question, multiplication for the |
I will try this, thank you. Here I have two questions.
|
I tried to construct pauli string using |
The variations among To relieve the precision problem when the qubit size is not too large, you can switch the data type (dtype) from import paddle_quantum as pq
from paddle_quantum import Hamiltonian
from paddle_quantum.state import ghz_state
from paddle_quantum.qinfo import random_pauli_str_generator
num_qubits = 4
pauli_str = random_pauli_str_generator(num_qubits, terms=10)
# Compute error from imaginary part of expectation value
def expect_error() -> float:
psi = ghz_state(num_qubits)
H = Hamiltonian(pauli_str)
H_matrix = paddle.to_tensor(H.construct_h_matrix())
value = psi.bra @ H_matrix @ H_matrix @ psi.ket
return abs(value.imag().item())
# Calculate the expectance value under complex64
pq.set_dtype('complex64')
error_64 = expect_error()
# Calculate the expectance value under complex128
pq.set_dtype('complex128')
error_128 = expect_error()
print("The error for complex64 is", error_64)
print("The error for complex128 is", error_128)Note that the function |
The reason why the class For the same reason, I believe every imaginary coefficient occured in one term of Such logic may need to be considered during the construction of Pauli strings of |
Yes, indeed. I retain every term when I trying to build the H^2 pauli string function. And I should care the imaginary coefficient can be vanished, thanks! |
Nice solution, I will try, thanks 👍 |






Hello,
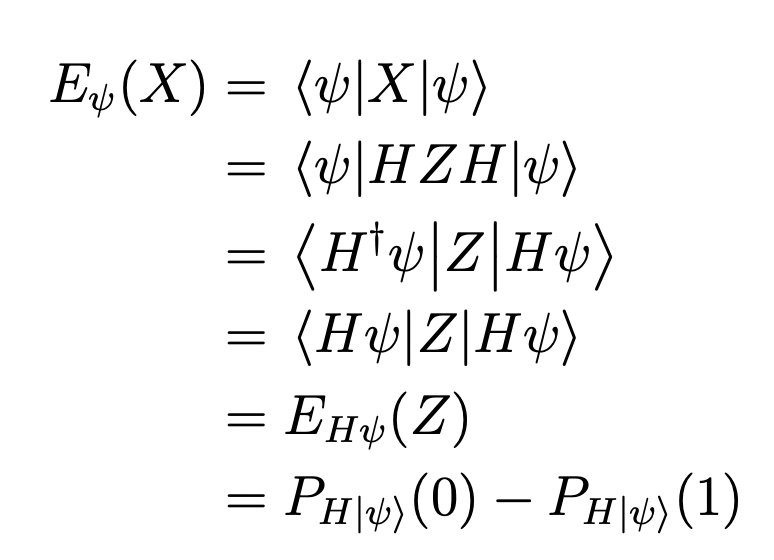
For a tutorial, I am trying to do something very simple, calculating the expectation value of:
Instead of:
How can i specify my own Hamiltonian to compare the value with the theoretical one?
Thanks
The text was updated successfully, but these errors were encountered: